数学模型，让问题更简单

张瑜

[摘  要] 数学方法的掌握和数学思想的领悟是数学学习的关键，初中数学亦是如此. 数学模型则是这关键要素中的核心要素，是数学学科所特有的方法和思想之一.

[关键词] 数学模型;初中数学;函数模型;素养

数学模型是运用数学思想和数学语言描绘现实问题，是基于建构主义理论的一种主动学习过程，是将某一对象进行数学抽象，然后应用数学公式进行模拟和验证的一种模式化思维形式. 模型的建立在初等数学中对于实际问题的解决起着关键作用，也是发展建立数学思维的重要方法. 数学模型包括方程模型、函数模型、不等式模型、概率模型、几何模型等. 而数学模型从经历实际问题的分析、实际问题的抽象、实际问题的建模、数学公式的应用、实际问题的解决，每种模型问题有相似之处，方法与思想也万变不离其宗. 而如何引导学生学会使用数学方法解决数学问题，提炼数学思想是教师需要重点思考与研究的关键所在. 为此，本文以初三数学专题复习课“图表信息类问题”中的教学片段为例，谈谈函数模型在数学中的实践性运用及笔者对此的一些看法.

热点再练，温故知新

图表信息类问题是近几年中考的热点问题，在中考试卷中所占的分数也呈现出逐年上升的趋势，这种上升是基于其价值与社会需要而形成的. 因为图表信息类问题以图表的形式向学生呈现各种问题信息，而学生需要经历识图识表、图表转换、问题建模、公式应用等过程，每个过程都对学生在相应环节所需要的能力提出了较高的要求. 因此，它的出现有其多重身份和价值的彰显. 为此，我们在初三二轮复习中需将此作为一个独立专题精讲精练，渗透其中的函数思想，对学生进一步领会函数思想，提高数学能力有着积极作用. 通过热点再练对已学知识的再现和回忆，发现新的问题，达到新的高度，由“温故”而“知新”.

1. 在一次国际马拉松比赛中，一名34岁的男子带着他的两个孩子一同参加了比赛，记者对两个孩子的年龄充满好奇，图1是两个孩子的对话，你能据此帮记者推算出他们的年龄吗？

3. 桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15厘米，表1记录了甲、乙、丙三个杯子的底面积. 甲杯中装有10厘米高的水，今小明将甲杯内的水倒入乙杯或丙杯，在此过程中没有水溢出，若不计杯子厚度，则乙杯、丙杯内的水面高度为多少厘米？（）

A. 7、8                   B. 7.5、8

C. 7、6                   D. 7.5、6

4. 图3反映的是爷爷早上起床后从家出发，先去玉米地浇水，再去菜地除草，然后回家吃早餐. 若玉米地和菜地的距离为a km，爷爷在菜地除草比在玉米地浇水多用了b min，则a，b的值分别为（      ）

A. 1、8                 B. 0.5、12？摇？摇？摇

C. 1、12               D. 0.5、8

5. 为了解某市居民晚饭后的活动方式，调查小组设计了“阅读”“锻炼”“看电视”和“其他”四个选项，用随机抽样的方法调查了该市的部分居民，并根據调查结果绘制成如图4的统计图. 根据统计图所提供的信息，解答下列问题：

（1）本次共调查了______名市民;

（2）补全条形统计图;

（3）该市共有800万市民，估计该市晚饭后锻炼的人数.

完成方式：学生独立完成，后小组校对答案，而教师则是巡视整个课堂情况. 一是从巡视学生独立作业的过程中，发现问题、分析问题，并锁定解决问题的策略. 二是巡视学生小组合作交流的过程，通过私下询问、观察了解学生已有的思维动态，发现问题、启发问题、分析问题，并为自己如何进一步激发学生的思维碰撞与融合做好充分准备.

师：以上这5个问题分别代表了图表信息哪些类型的问题呢？

生1：分别是图片信息、图形信息、表格信息、图像信息、统计信息.

师：你归纳得非常完整. 针对这些问题，大家的解题思路是什么呢？

生2：先读图，再分析，接着建立数学模型，最后解决问题.

师：没错，在这个过程中，读懂题意，建立正确的数学模型是解决问题的关键.

设计意图  上述5个问题几乎囊括了初中阶段图表类问题的所有情形，题目难度不大，学生基本可以独立解决，因此这环节的设计主要是让学生对图表类问题有系统的认识，在此基础上展开难度较大的问题，渗透函数模型的用法.

典例剖析，提炼方法

二轮复习主要的目标是发现规律、总结方法，启发学生站在更高的高度审视我们所学的内容，并帮助学生在自己已有的数学素养下，建构成思路更清晰、脉络更通畅的知识与技能网络. 因此，在二轮复习时的例题应具有挑战性和引领性，一方面是让学生有提高的空间，让学生的思维在训练中得以拓展，另一方面是这个环节的教学设计可以引领学生把关注点置于方法的提炼上，真正实现能力上的提升.

例1  甲乙两地相距300 km，一辆货车和一辆轿车先后从甲地出发驶向乙地. 如图5，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系.

（1）通过精准读图，你得到了哪些信息？

（2）你可以提出哪些可供同学求解的问题？

（3）思考：这些问题的解决需要哪些数学知识？

完成方式：（1）以小组为单位，共同探讨，（2）由小组间相互问答，（3）由师生共同总结归纳.

在问题（2）中，学生们集集体的智慧，提出并解答了如下问题：

生1：轿车多长时间能追上货车？

生2：在2.5≤x≤4.5范围内，当x取何值时，两车相距10 km？

生3：当轿车到达目的地时，货车离乙地有多远？

生4：求轿车的平均速度.

问题（3）师生共同总结：上述问题的解决需要用到根据实际问题结合坐标解读图像的实际意义、待定系数法求解析式、函数值的求法等. 其中最主要的就是函数思想，即将实际问题抽象为函问题.

例2  如图6，A，B，C，D为矩形的四个顶点，AD=4 cm，AB=d cm. 动点E，F分别从D，B出发，点E以1 cm/s的速度沿DA边由D向A移动，点F以1 cm/s的速度沿BC边由B向C移动，当点F移动到点C时，两点同时停止移动. 以EF为边作正方形EFGH，点F出发x s时，正方形EFGH的面积为y cm2. 已知y与x的函数图像是抛物线的一部分，如图7所示. 请根据图中信息解答下列问题：

（1）自变量x的取值范围是______;

（2）d=_____，m=_____，n=______;

（3）求点F出发几秒时，正方形EFGH的面积最大？最大面积为多少？

完成方式：学生独立完成，后全班交流展示，师生共同归纳思想方法.

在此问题中，（1）（2）是对图形的解读，（3）的思路是依据函数的最值求解.

师生共同总结：解决图表信息类问题的基本思路是读图→分析→建立模型→解决问题. 在这个过程中，读图、用图、建模是关键.

设计意图  两个例题分别是开放型问题和非开放型问题，开放型问题最能提高学生能力和激发学生创造力. 在二轮复习中，学生已具备一定基础，让其对开放型问题进行探究，可以将问题的容量扩大. 用函数思想解决最值问题是初中数学中的常见题型，让学生独立完成更有利于其建模意识的形成.

■挑战新高，提升能力

在数学学习中，提高解题能力的方法之一就是不断挑战更高水平层次的问题，“拔尖”也是二轮复习的重要任务之一，因此，给学生提供对应的资源，让学生有探索的对象，是促进学生提升能力的有效方法.

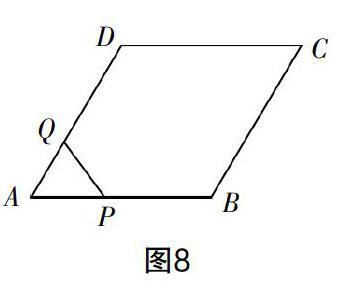
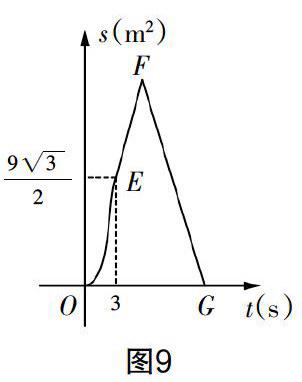
拓展延伸：如圖8，在菱形ABCD中，∠A=60°，点P从点A出发，以2 cm/s的速度沿边AB，BC，CD匀速运动到D终止，点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t（s）. △APQ的面积S（cm2）与t（s）之间函数关系的图像由图9中的曲线段OE与线段EF，FG给出.

（1）求点Q运动的速度;

（2）求图9中线段FG的函数关系式;

（3）问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分为1 ∶ 5的两部分？若存在，求出这样的t的值;若不存在，请说明理由.

完成方式：课上学生独立思考，如有疑惑留至课后和同学一起交流解决问题.

设计意图  该题需要就动点的不同位置所形成的不同问题进行分类讨论，有一定的难度，在课上留有一定的时间让学生思考，可以培养他们的思维，将问题留至课后让学生之间借助集体的智慧共同解决，有利于增强班级的凝聚力和学生之间形成相互学习的习惯.

图表信息类问题实质上就是数学模型思想的直接呈现，其中大部分问题是通过函数模型思想来解答的. 因此借助该专题，可以强化学生对函数模型思想的认识及用法，对进一步体会其他类型的模型思想也有促进作用.

“模型”对学生来说是较为抽象的概念，在实际问题中渗透模型思想的含义及用法，学生更易于接受. 函数模型是重要的数学模型之一，建立函数模型求解问题也是解决初中代数综合问题的重要思想方法，数学模型能让问题更简单.