双极化SAR数据反演裸露地表土壤水分

韩 玲，秦小宝，陈鲁皖

(长安大学 地质工程与测绘学院，陕西 西安 710054)

双极化SAR数据反演裸露地表土壤水分

韩 玲，秦小宝，陈鲁皖

(长安大学 地质工程与测绘学院，陕西 西安 710054)

为了较高精度地获取大范围地表土壤水分，提出一种基于双极化合成孔径雷达数据的裸露地表土壤水分反演模型即非线性方程组，通过改进的粒子群算法求解非线性方程组从而得到土壤水分。首先通过AIEM模型数值模拟和回归分析，得到一种新的组合粗糙度，然后模拟分析得到土壤水分与雷达后向散射系数的关系，从而建立雷达后向散射系数与组合粗糙度、土壤水分的经验关系。利用ASAR C波段双极化雷达数据，基于经验关系和改进的粒子群算法即可实现土壤水分的反演。经过黑河流域实测土壤水分数据对模型进行验证，反演结果与实测数据具备良好的相关性(R2=0.778 6)。与以往同一区域研究成果比较，文中的方法反演精度有所提高，更适用于裸露地表土壤水分反演。

土壤水分;改进的粒子群算法;AIEM;反演

土壤水分是陆表生态系统的重要组成部分，已成为研究水资源管理、自然与生态问题、农作物旱情监测的重要指标[1]。土壤水分的区域差异与动态变化更是反映陆面过程模式和区域水循环不可缺少的一个重要参数。因此，研究地表土壤水分分布具有重要的现实意义和科学价值[2]。

遥感技术相对常规监测方法，在监测数据的时效性、范围和技术成本等方面具有很大优势[3]，可用于遥感反演土壤水分的波段主要有可见光、热红外和微波。可见光热红外波段受云的影响很大，在多云的时节和区域受到很大限制[4]。微波遥感具有全天时、全天候、穿透能力强的特点，并且地表微波散射和辐射对土壤水分的敏感性使之渐渐成为监测土壤水分的主要手段[5]。微波对被探测物体的介电常数非常敏感，因此可以建立土壤水分与微波信号之间的关系[6]。合成孔径雷达(SAR)具有更高的空间分辨率，被广泛地应用于中小尺度的土壤水分反演[7]。

微波遥感反演土壤水分的模型分为两类：理论模型和经验、半经验模型。理论模型主要有几何光学模型(GOM)、物理光学模型(POM)、小波扰动模型(SPM)[8-10]。但是这些模型适用的土壤粗糙度范围较小。为了更好的模拟地表的散射和辐射，Fung[11]等提出IEM模型，后来Chen[12]，Wu[13-14]等对IEM模型进行改进，发展出了 AIEM模型，进一步提高模型模拟的精度和适用范围。理论模型虽然物理意义明确，但表达式十分复杂，很难直接用于土壤水分的反演。经验模型(如线性模型[15]，Oh 经验模型[16]和Dubois模型[17]等)，和半经验模型(如Chen模型[18]、Oh模型[19]和Shi 模型[20])等借助实测数据或通过对理论模型近似得到适用于一定区域的散射模型，在反演土壤水分过程中受到广泛关注。

为了减少土壤水分反演模型中的未知个数，Zribi[9]提出组合粗糙度Zs=s2/l，利用两种不同入射角的后向散射系数反演土壤水分。余凡[21]，孔金玲[22]分别提出适合相应研究区的组合粗糙度参数，s3/l2和s3/l代表组合粗糙度，利用不同极化后向散射系数建立非线性方程组反演土壤水分。本文利用AIEM模型对粗糙度参数进行模拟分析，得到组合粗糙度，将2个粗糙度参数合二为一。基于此，利用ASAR C波段双极化数据，建立土壤水分反演模型即非线性方程组，利用改进的粒子群算法求解非线性方程组，即可实现土壤水分的反演。基于改进的粒子群算法求解土壤水分，与先前研究中的消去法相比计算更简单更易编程实现，更适合实际应用中土壤水分的反演。

1 研究区和数据预处理

1.1 研究区概况

本文所用的影像和地面实验数据来自 “黑河综合遥感联合实验”，研究区位于临泽草地,试验场位于平原，地形比较平坦，试验场的土质由16.7%沙土，74.8%泥沙和8.5%粘土组成。实测数据总共包括49个采样点，包括每个采样点的经纬度坐标以及每个点0～5 cm的平均体积含水率，均方根高度和相关长度数据。

1.2 卫星数据

ASAR是欧空局ENVISAT-1卫星最大的传感器，ASAR传感器的中心波长为5.6 cm[23]。本文选择2008-07-11空间分辨率为30 m、地面分辨率12.5 m×12.5 m、 VV/VH组合极化方式、入射角模式为IS4的AP模式数据。

1.3 ASAR数据预处理

ASAR的AP模式数据属于Level 1B级地距精细图像，因此对影像的预处理包括辐射定标、几何校正、滤波。本文利用欧空局开发的NEST软件对影像进行预处理，首先对影像进行辐射定标，将影像DN值转换成后向散射系数(db)。然后利用增强型Lee滤波，滤波窗口大小设为5×5，对影像中的较大噪声点进行去除。最后进行几何精校正，结合数字高程模型(DEM)，进行距离多普勒校正，得到空间分辨率为30 m的后向散射系数影像。利用NEST软件通过实测点的经纬度坐标得到对应像元的雷达后向散射系数。

2 研究过程与方法

2.1 AIEM模型

本文利用AIEM模型计算裸露土壤的后向散射系数，AIEM模型的输入参数包括传感器参数(频率、入射角)和地表参数(土壤水分、相关长度、均方根高度、自相关函数、土壤温度和土壤质地)。AIEM模型单次散射表达式[21]为

(1)

(2)

式中的参数含义见文献[13]。

自相关函数为指数函数时能取得很好的模拟结果[10]，因此自相关函数取

(3)

式中：x为任意两点的距离；S为均方根高度；l为相关长度。

2.2 地表散射特性描述

Shi[20]等的研究发现，裸露地表的雷达后向散射系数主要与地表粗糙度和土壤含水量相关，关系为

δpp=g(Rs,θ)*f(mv,θ).

(4)

式中：g(Rs,θ)是与土壤粗糙度相关的函数；f(mv,θ)是与土壤水分相关的函数。

2.2.1 地表组合粗糙度

为了模拟地表粗糙度和后向散射系数之间的函数关系，AIEM模型输入参数如下：θ=35°,mv=0.35,S∈(0.1,1.5),L∈(2,20)，S步长为0.1，L步长为2，通过多元线性回归分析δvv与S和L存在关系

δvv=5.805+9.47lnS-6.28lnL.

(5)

相关系数为0.991，根据式(5)的S和L的关系构造出组合粗糙度Zs=S3/L2,则

δvv=5.805+2.78lnS3/L2，

(6)

其数学关系式为

δvv=a+blnZs.

(7)

其中a，b为经验系数。

图1为不同土壤水分条件下后向散射系数与组合粗糙度的相应关系，发现不同的水分条件下，后向散射系数与组合粗糙度有着相同的变化规律，呈现明显的对数关系，同样VH极化也有类似的结论。

2.2.2 土壤水分相关函数

Ulaby认为雷达后向散射系数与土壤体积含水量存在线性关系，表示为

δpq=amv+b.

(8)

δpq为雷达后向散射系数值，mv为土壤水分值，a和b为最小二乘拟合所得的参数。但式(8)一般适用于粗糙度比较小的区域。

为了建立土壤水分与后向散射系数的函数关系，AIEM模型输入参数θ=35°，S=0.8 cm，L=6 cm，mv∈(0.01,0.5)，mv步长0.02，模拟极化后向散射系数δvv与mv的关系为

δvv=2.978lnmv-4.215 8，

(9)

其数学关系式为

δvv=clnmv+d.

(10)

其中c,d为经验系数。

图2为不同粗糙度条件下后向散射系数与土壤水分之间的关系。由图可知，在不同的粗糙度条件下，后向散射系数与土壤水分有着相同的变化规律，明显呈对数关系，同样VH极化也有类似的结论。

图2 不同粗糙度条件下δvv 与mv的关系

2.2.3 新的土壤水分反演模型

由以上分析可知，在入射角一定时，结合式(7)和式(9),后向散射系数表达式可以写为

δvv=(alnmv+b)*(clnZs+d).

(11)

整理得到

δvv=Alnmv+BlnZs+ClnmvlnZs+D.

(12)

通过最小二乘法可以拟合得到A，B，C，D4个系数，从而得到后向散射系数δvv与土壤水分mv以及组合粗糙度Zs之间的函数关系。图3为入射角35°时，AIEM模拟的后向散射系数，与式(12)计算的后向散射系数的散点图。

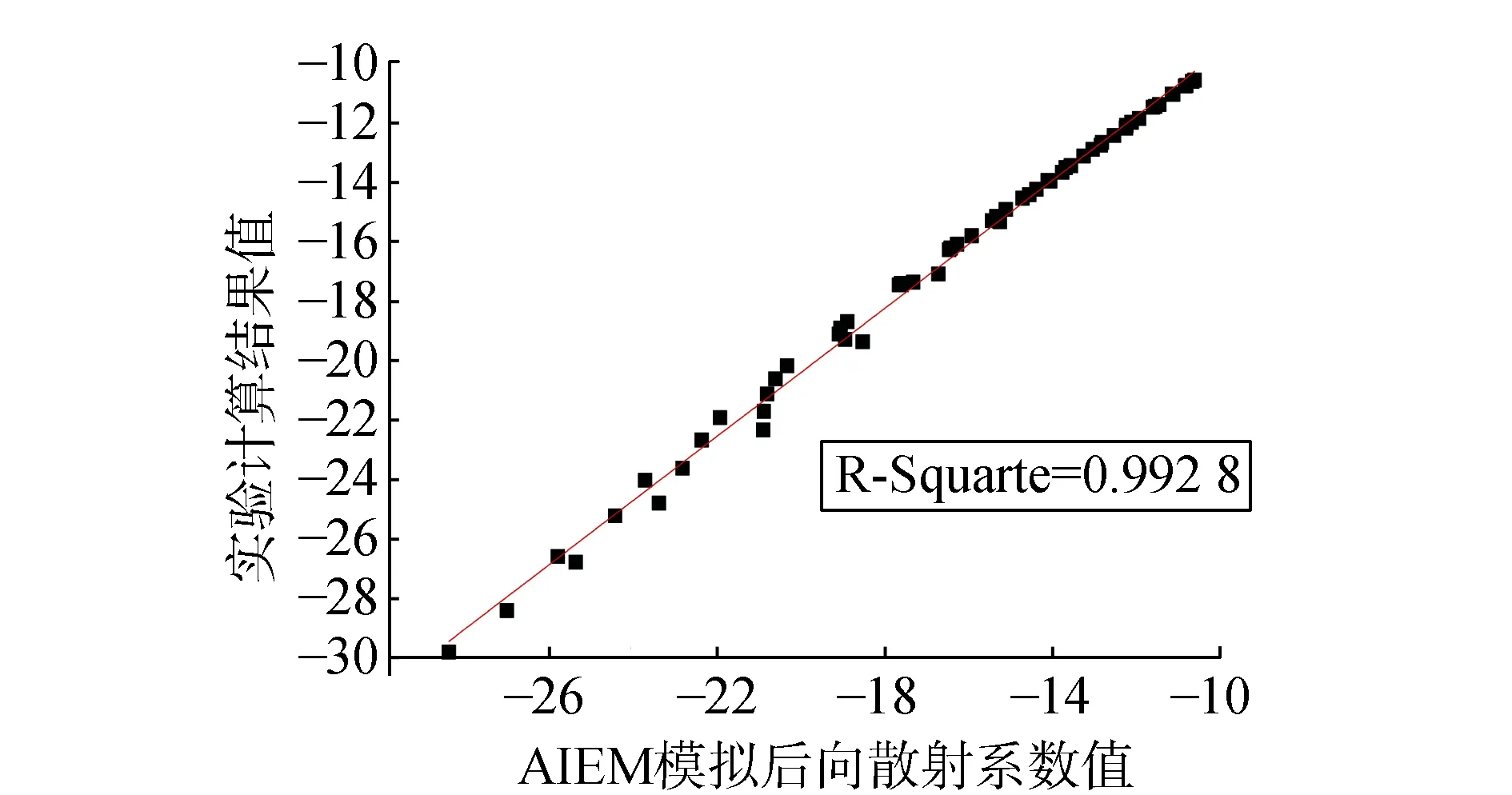
图3 AIEM与上式后向散射系数模拟值比较

实验发现VH极化下，后向散射系数δvh与土壤水分mv以及组合粗糙度Zs的关系与VV极化条件相似，关系式为

δvh=Elnmv+FlnZs+GlnmvlnZs+H.

(13)

联立式(12)和式(13)即可得到非线性方程组，通过解非线性方程组就可以解算土壤水分。

2.2.4 不同入射角适用性

本文研究了入射角35°后向散射系数与土壤水分mv以及组合粗糙度Zs之间的函数关系。为了研究该模型不同入射角的适用范围，AIEM模型设置输入参数为

θ=(15°，23°，30°，38°，42°，45°)，

S∈(0.1,1.5),L∈(2,20),mv∈(0.05,0.5).

式中：S步长为0.1，L步长为2，mv步长为0.02，建立对应不同入射角的模拟后向散射系数数据库。

本文通过建立不同入射角的模拟数据库，利用不同角度的模拟数据通过最小二乘拟合得到不同角度反演模型所对应的A，B，C，D4个系数的值(见表1)。

表1 不同入射角对应的经验系数

利用表1进一步拟合经验系数与入射角的函数关系为

A(θ)=-3.261 6θ2+4.682 8θ+1.655 7，

(14)

B(θ)=4.125 8θ+0.602 7，

(15)

C(θ)=-0.029 4θ+0.003 4，

(16)

D(θ)=-7.962 2θ+13.029.

(17)

正演模型可以表示为

δvv=A(θ)lnmvB(θ)ln+C(θ)lnmvlnZs+D(θ).

(18)

由表1可知，在入射角大于23°时，本文模型都可以取得较高正演精度。同样VH极化也可得到类似结论，因此利用双极化SAR数据反演土壤水分是可行的。

3 实验和分析

3.1 土壤水分反演模型

为了验证模型的可靠性，需要用一部分实测数据拟合得到系数的值，用另一部分数据验证反演结果。本次实验同步观测数据共有49个采样点的土壤体积含水量和均方根高度、相关长度以及经纬度坐标。将获取的29个实测点的土壤体积含水量以及上述组合粗糙度模型计算得到的组合粗糙度、对应点的雷达后向散射系数代入式(12)和式(13)，通过最小二乘拟合得到土壤水分反演模型为

(19)

求解上述非线性方程组就可以得到土壤水分的值。求解非线性方程组最常用的方法是牛顿迭代法，但是牛顿迭代法解的精确性与给定的初始值密切相关，因此本文选择改进的粒子群算法求解该非线性方程组，从而实现土壤水分的反演。

3.2 改进的粒子群算法求解非线性方程组

3.2.1 标准粒子群算法

标准粒子群算法首先初始化一群随机粒子(随机解)，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pbest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gbest。另外可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值[24]。

标准粒子群算法采用学习因子及惯性权重，粒子根据式(20)更新自己的速度和位置。

(20)

(21)

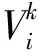
3.2.2 改进的粒子群算法

标准粒子群算法中惯性权重和学习因子是很重要的参数。惯性权重过大时全局搜索能力强，惯性权重较小时局部搜索能力强。学习因子决定了粒子本身经验信息和其他粒子经验信息对粒子运动轨迹的影响。学习因子过大会使粒子聚集在局部，过小又会过早收敛至局部极值。标准粒子群算法采用固定惯性权重和学习因子的方式，改进的粒子群算法相较于标准粒子群算法采用动态迭代选择惯性权重因子和学习因子，既可以提高寻优能力减少迭代次数又可以避免局部极值的干扰。

改进的惯性权重和学习因子为

(22)

(23)

(24)

式中：generation表示最大迭代次数；wmax和wmin是初始和终止惯性权重，一般给定为1.5和0.1；c1max和c1min给定为2和0；c2max和c2min给定为2和0。

改进的粒子群算法求解非线性方程组步骤：

1)随机初始化种群中各微粒的位置和速度；

2)评价各粒子的适应度，适应度评价函数本文给定适应度评价函数为 ，将各粒子的位置和适应度储存在各微粒的pbest中，将所有pbest中适应度最优的个体的位置和适应度存储在gbest中；

3)更新粒子的速度和位移；

4)对每个微粒，与其前一个最优位置比较，如果较好，则将其作为当前的最优位置；

5)比较当前所有的pbest和上一迭代周期的gbest，更新gbest；

6)若满足停止条件(达到要求精度或迭代次数)，搜索停止，输出结果，否则，返回2。

3.3 土壤水分反演

本文通过ENVI裁剪2008-07-11的ASAR影像得到采样区附近600像素×600像素的研究区影像，利用C++和GDAL库[25]基于ASAR双极化雷达数据，利用改进的粒子群算法求解每个像元的土壤水分值，得到的土壤水分反演结果如图4所示。

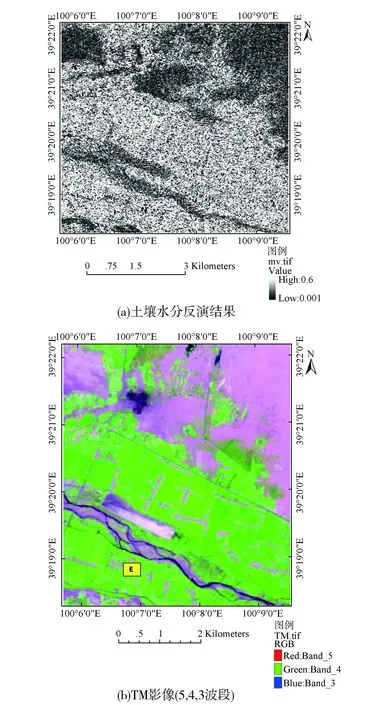
图4 土壤水分反演结果图和对应的TM影像(5,4,3波段)

由该区域TM影像可以看出，土壤水分反演的结果大致符合实际情况，有草地覆盖的区域，土壤含水量较高，对应到反演结果图上明显发亮，但是还需要用样区E的实测数据对反演精度进行进一步验证，建立反演结果与实测数据的关系如图5所示。

图5 土壤水分反演值与实测数据比较

4 结 论

本文基于AIEM模拟地表后向散射，提出一种组合粗糙度，通过分析后向散射系数与土壤水分以及组合粗糙度之间的函数关系，构建土壤水分反演模型，基于改进的粒子群算法求解得到土壤水分值，得出以下结论：1)组合粗糙度参数Zs=S3/L2适用于小粗糙度情况下的土壤水分反演，应继续探讨适合各种复杂地表组合粗糙度参数；2)该反演模型适用于雷达入射角大于23°的情况下的土壤水分反演；3)利用改进的粒子群算法反演土壤水分，与先前的相同的研究区域反演精度[21,26](R2=0.745,R2=0.71)相比有所提高，并且比先前研究的消去法更简单，更容易编程实现，为以后土壤水分反演提供了新的思路；4)对于全极化数据其他极化组合数据的反演精度需要进一步探讨。

[1] BECK H E, DE Jeu R M, SCHELLEKENS J, et al. Improving Curve Number Based Storm Runoff Estimates Using Soil Moisture Proxies[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2010, 2(4): 250-259.

[2] BARRETT B W, DWYER E, WHELAN P. Soil moisture retrieval from active spaceborne microwave observations: an evaluation of current techniques[J]. Remote Sensing, 2009, 1(3): 210-242.

[3] 马红章, 柳钦火, 闻建光, 等. 裸露地表土壤水分的L波段被动微波最佳角度反演算法[J]. 农业工程学报, 2010, 26(11): 24-29.

[4] 鲍艳松, 刘利, 孔令寅, 等. 基于ASAR的冬小麦不同生育期土壤湿度反演[J]. 农业工程学报, 2010, 26(9): 224-232.

[5] 田国良.土壤水分的遥感监测方法[J]. 遥感学报, 1991(2): 89-98.

[6] DOBSON M C, ULABY F T. Active Microwave Soil Moisture Research[J]. IEEE Transactions on Geoscience & Remote Sensing, 1986, 24(1): 23-36.

[7] BOLTEN J D, CROW W T, ZHAN X, et al. Evaluating the Utility of Remotely Sensed Soil Moisture Retrievals for Operational Agricultural Drought Monitoring[J]. Selected Topics in Applied Earth Observations & Remote Sensing IEEE Journal of, 2010, 3(1): 57-66.

[8] FUNG A K. Microwave Scattering and Emission Models and Their Applications[M]. Artech House, 1994.

[9] ZRIBI M, DECHAMBRE M, IEEE, et al. A new empirical model to inverse soil moisture and roughness using two radar configurations[M]. 2002: 2223-2225.

[10] 乌拉比.微波遥感[M]. 北京：科学出版社, 1988.

[11] FUNG A K, LI Z, CHEN K S. Backscattering from a randomly rough dielectric surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 356-69.

[12] CHEN K S, TZONG-DAR W, MU-KING T, et al. Note on the multiple scattering in an IEM model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 249-56.

[13] WU T D, CHEN K S. A reappraisal of the validity of the IEM model for backscattering from rough surfaces[J]. IEEE Transactions on Geoscience & Remote Sensing, 2004, 42(4): 743-753.

[14] WU T D, CHEN K S, SHI J, et al. A transition model for the reflection coefficient in surface scattering[J]. IEEE Transactions on Geoscience & Remote Sensing, 2001, 39(9): 2040-2050.

[15] BRUCKLER L, WITONO H, STENGEL P. Near surface soil moisture estimation from microwave measurements[J]. Remote Sensing of Environment, 1988, 26(2): 101-121.

[16] OH Y, SARABANDI K, ULABY F T. An empirical model and an inversion technique for radar scattering from bare soil surfaces[J]. Geoscience & Remote Sensing IEEE Transactions on, 1992, 30(2): 370-381.

[17] DUBOIS P C, VAN Zyl J, ENGMAN T. Measuring soil moisture with imaging radars[J].IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 915-26.

[18] CHEN K S, YEN S K, HUANG W P. A simple model for retrieving bare soil moisture from radar-scattering coefficients[J]. Remote Sensing of Environment, 1995, 54(2): 121-126.

[19] OH Y, SARABANDI K, ULABY F T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces[J]. Geoscience & Remote Sensing IEEE Transactions on,2002,40(6):1348-1355.

[20] SHI J, WANG J, HSU A Y, et al. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data[J]. Geoscience & Remote Sensing IEEE Transactions on, 1997, 35(5): 1254-1266.

[21] 余凡, 赵英时. 合成孔径雷达反演裸露地表土壤水分的新方法[J]. 武汉大学学报(信息科学版), 2010, 35(3): 317-321.

[22] 孔金玲, 甄佩佩, 李菁菁, 等. 基于新的组合粗糙度参数的微波遥感土壤水分反演[J]. 地理与地理信息科学, 2016, 32(3): 5-9.

[23] 李苗, 臧淑英, 那晓东, 等. ENVISAT-ASAR数据产品介绍与数据处理[J]. 测绘与空间地理信息, 2012, 35(1): 63-65.

[24] 陈长忆,叶咏春. 基于粒子群算法的非线性方程组求解[J].计算机应用与软件, 2006, 23(5).

[25] 李民录. GDAL源码剖析[M].北京：人民邮电出版社, 2012.

[26] 陈晶, 贾毅，余凡. 双极化雷达反演裸露地表土壤水分[J]. 农业工程学报, 2013, 29(10): 109-115.

Inversion of soil moisture on bare surface by dual polarization SAR data

HAN Ling, QIN Xiaobao, CHEN Luwan

(School of Geological Engineering and Surveying Engineering, Chang’an University, Xi’an 710054, China)

In order to retrieval soil moisture accurately, a model which is non-linear equations is introduced to estimate the surface soil moisture by using dual-polarization advanced synthetic aperture radar data. In this paper, the improved particle swarm optimization (PSO) is used to solve the non-linear equations for obtaining soil moisture. Firstly, a database linked to SAR backscattering coefficients, surface roughness parameters, and soil moisture are built by AIEM (advanced integral equation model).Through regression analysis of the simulated database, a new roughness parameter and the relationship between soil moisture and backscattering coefficient is obtained. Then the empirical relationship between radar backscattering coefficient and combined roughness and soil moisture is established. By using ASAR C-band dual polarization radar data, the soil moisture can be retrieved based on the empirical relationship and improved particle swarm optimization algorithm. The model is validated by the measured data in Heihe River. It concludes that there is a good relationship between the estimated data and measured data. The correlation coefficient is as high as 0.778 6. Compared with the previous regional research result, the inversion accuracy of this paper has been improved, which is more suitable for bare surface soil moisture inversion.

soil moisture; improved particle swarm optimization; AIEM; inversion

2017-06-14

国家重大高分专项(GFZX04040202-07)

韩 玲(1964-)，女，教授.

著录：韩玲，秦小宝，陈鲁皖.双极化SAR数据反演裸露地表土壤水分[J].测绘工程，2018，27(2)：7-12.

10.19349/j.cnki.issn1006-7949.2018.02.002

P237

A

1006-7949(2018)02-0007-06

张德福]