面向陆军分队战术模拟的坐标系统设计

李坤伟，游 雄，武志强，张 欣，汤 奋

(信息工程大学 地理空间信息学院，河南 郑州 450052)

面向陆军分队战术模拟的坐标系统设计

李坤伟，游 雄，武志强，张 欣，汤 奋

(信息工程大学 地理空间信息学院，河南 郑州 450052)

联合作战条件下，战役、战术之间的界限越来越模糊，战术行动在一定情况下具有战略价值。在作战模拟领域，战术模拟系统向上与战略、战役模拟系统对接，为战略、战役推演提供支撑，向下支持单武器的对抗模拟。一致、准确的环境模型是保证战术模拟系统正常运行的基础；战术模拟系统的这种变化对环境模型的建模范围、建模精度提出了更高的要求。坐标系是环境建模的基础，分析了现有模拟系统中坐标系的不足及其对战术模拟的影响；从现代战术模拟的特点出发分析了战术模拟对坐标系的需求；在此基础上，设计了能够满足现代战术模拟要求的坐标系。

联合作战；战术模拟；高斯投影；空间直角坐标

作战模拟是对实际作战环境、军事行动和作战过程的描述与模仿，是研究、揭示战争内在规律，分析、评估作战方案和计划，训练部队官兵，提高部队战术水平与实际作战能力的重要手段[1]。与实兵演习相比，计算机对抗模拟具有省时、省钱、省力，训练范围广、对抗性强等优点，受到人们的广泛关注。联合作战条件下，战役、战术之间的界限越来越模糊；战术模拟系统向上与战略、战役模拟系统对接，为战略、战役推演提供支撑，向下支持单武器的对抗模拟。战术模拟系统的这种变化对作战模拟系统中环境模型的描述精度和建模范围提出了更高的要求。当前，在我军战术模拟系统中主要使用高斯投影坐标；随着模拟区域的扩大、模拟精度的提高，高斯投影坐标已不能很好满足战术模拟的需求。基于此，本文对战术模拟系统中的坐标系进行了研究。

1 现状分析

目前，我军现行大于1∶50万比例尺的地图主要采用高斯投影，受此限制我军战术模拟系统中也主要使用高斯投影坐标。高斯投影的主要优点是：投影后角度不变；高斯投影实现了椭球面向平面的转换，简化了模型计算分析的过程。但是，随着高技术装备的应用和精确打击的发展，在高斯投影坐标下已无法准确地描述作战行动的特征，不能有效地满足战术模拟的需求。

1)无法满足平台级模拟的精度需求。在投影变换中，只有点的经纬度值参与计算，而点的高程值实际上没有变化。在地球椭球面上，点的高程起算面是参考椭球面，而在高斯投影坐标中，点的高程起算面实际上是高斯平面[2]。这种忽略对平面上的方向、距离等计算不会产生太大影响，但是当模型计算过程中涉及到要素的高程时则会使计算结果出现偏差。如图1所示，在真实世界中，由于遮蔽物的存在，A和B点不能通视。经过投影变换，观察点、目标点和遮蔽物的高度没有发生变化，而此时A和B点之间能够通视，投影变化增大了通视的可能。通视是侦查的基础，是直瞄武器实施打击的前提。通视概率的增大意味着开火的次数增多，导致在真实环境中不可能发生交战，而在模拟系统中变得能够交战。虽然偶尔的误差不会对结果产生重大影响，但是当作战区域内地物要素密集时(如城市作战)或者地形起伏较大的地区时，上述情况将会频繁出现，多次误差的累积就会加速弹药消耗，加快战斗进程，最终影响模拟的结果。

图1 通视计算误差

2)不能有效解决建模区域跨度带问题。在分带投影机制下，不同的条带使用不同的投影坐标。当建模区域横跨两个投影带时，需要统一投影坐标。传统的方法是先确定一个主投影带，然后将所有的数据统一到主投影带中去，这种方法存在很大的变形误差[3]。

3)无法支持大区域、大范围建模。由于高斯投影在每个条带内单独进行投影变换，因此在同一参考坐标系下，高斯投影的建模范围局限在一个条带内。在6°分带投影中，一个投影带的东西跨度最大不超过700 km，这严重限制了高斯投影的建模范围。

4)无法满足信息化条件下，联合作战的需求。信息化条件下，战役、战术的界限越来越模糊，联合作战呈现多兵种、多层次的特征。当前，在战役行动中，主要使用兰勃特等角投影，而在战术行动中主要使用高斯投影，投影坐标的不同限制了一体化联合作战的应用和发展。

5)转换效率低。高斯投影坐标属于局部坐标系，在分布式仿真中，不同仿真节点之间相互通信时，为了准确传递信息，需要使用全局坐标。然而，在高斯投影变换中存在大量迭代、三角函数计算，当不同节点之间频繁通信时，坐标转换会严重影响通信效率，进而影响节点之间的协同。

2 战术模拟系统的特征及其对坐标系的要求

坐标系是描述客观环境和作战行动的基础，坐标系设计是战术模拟系统设计的重要组成部分。信息化条件下，战术行动和战术模拟都发生了较大变化，这些变化对模拟系统中的坐标系设计提出了新的要求。

2.1 战术模拟系统的特征

高科技在军事领域的广泛应用，使武器装备发生了革命性的变化，改变了传统的作战样式。信息化武器成为战场的主导武器，信息化武器的典型特征是打得准，能对近、中、远距离上和遮蔽物后的运动或固定目标实施精确打击；打得远，能对战场区域实施全纵深打击；杀伤力大，能在较短时间内和较大面积上形成突然、密集、猛烈的火力打击，对坚固工事和装甲目标实施有效摧毁[4]。另一方面，依托计算机技术、网络技术等信息技术，在对作战行动进行模拟时可以构建更加复杂的系统框架，设计更加精细的模型，模拟更加复杂的交战过程，使得模拟结果更加真实、更加可靠。

战术模拟是对实际行动及其作战空间的描述与仿真。战术模拟作为作战模拟的底层，可以为上级的作战模拟提供必要的数据支持，以提高战役作战模拟和合同战术作战模拟的精确度和可信度。信息化条件下，战术模拟的特点主要有：

1)从系统的架构来看，战术模拟系统应该遵循DIS和HLA标准[5]。网络技术的发展，可以将不同地理位置上、不同类型的仿真对象连接起来，使它们能相互操作；同时，随着应用领域的拓展，需要解决的问题也越来越复杂，也必须将多个仿真模拟系统联合起来进行模拟。

2)从系统运行环境来看，战术模拟系统运行在普通计算机上，不是超级计算机上。这一方面促进了模拟系统的推广应用，另一方面也使得在设计系统时必须考虑普通计算机的性能。

3)从模型精度上来看，战术模拟对模型的精度要求较高，对战斗实体的描述要细化到单兵、单车、单件火器，对地形的描述要精确到每个地物、每个建筑物、甚至每一棵树[6]。

4)从实体数量来看，在一次对抗模拟中，可能会出现上万个作战实体。1995年，在美军开发的Stow系统中就可以支持5万多个实体的仿真[7]，而在JCATS甚至可以达到10万个。

5)从建模区域来看，随着武器装备性能的提高和分布式仿真技术的发展，模拟区域在不断扩大。美军的战术仿真系统中的地形环境建模区域经历了90年代初期的200 km×300 km，到中期的400 km×500 km，到现在的2 000 n mile×2 000 n mile[8-10]。未来战术仿真系统中，模拟区域会越来越大。

6)从模拟样式来看，战术模拟系统应当同时支持虚拟仿真和构造仿真。

7)从模型交互来看，在战术模拟系统存在着大量的交互行为，主要表现在实体与实体、实体与环境模型之间的交互。由于模拟系统中实体众多，环境模型复杂，模型的交互行为会占用大量的计算资源，直接影响系统的运行性能，甚至导致系统不可用[11]。

2.2 对坐标系统设计的要求

对于一个模拟系统而言，系统的可用性是第一位的，当作战方案在系统上运行十分缓慢时，人们会降低环境模拟的精度，以保证系统顺畅运行[11]。但是随着作战方案中对环境的描述精度越来越高，一味地降低环境模型的精度会影响模拟的结果，因此模拟系统设计需要在运行性能和模型精度之间找到平衡。坐标系是描述作战行动和环境模型的基础，坐标系的选择会影响模型的建模精度和系统的运行性能，是模拟系统设计必须要考虑的因素。综合考虑模拟精度和系统运行性能，战术模拟系统对坐标系的要求主要有以下几点：

1)便于向全局坐标转换。在分布式系统中，各个仿真节点之间需要不断地交换位置信息，由于仿真节点对应的真实区域分布较广，不可能都在一个投影带中，因此，为避免歧义，不同仿真节点之间传输的不应该是局部坐标，而应该是经纬度坐标或者空间直角坐标。这就要求仿真节点要么使用全局坐标，要么进行坐标转换。如果进行坐标转换，那么就需要考虑坐标转换的效率。随着推演节奏加快，坐标转换的效率直接影响不同仿真节点之间的协同。因此，在分布式战术模拟中，对坐标系设计的第一个要求是便于向全局坐标系转换。

2)使用局部坐标系。由于计算机的计算、存储资源有限，在保证相同的描述精度情况下，使用全局坐标会占用更多的内存空间，因此，在仿真节点中的坐标系应当使用局部坐标系。

3)减少投影坐标的使用。在投影坐标下对环境要素和作战行动进行描述不可避免地会产生误差，随着对模拟精度的要求越来越高，有些误差会严重影响模拟结果，这就要求尽量减少投影坐标的使用。

4)易于向平面坐标转换。在大量交互的情况下，模型之间的交互效率至关重要。在曲面上进行相关的计算，虽然计算精度高，但是在大量交互背景下，会严重影响系统的运行性能。地图投影的最大优势是将曲面问题转换到平面上，极大地提高了计算的效率，有力地保障系统的运行效率，因此，这就要求坐标系易于向平面坐标转换。

3 坐标系设计

在大地测量中，地面点的空间位置必须用3个变量确定，描述一个点的位置主要有4种方法：大地坐标+高程、天文坐标+高程、空间直角坐标以及平面直角坐标+高程[12]，其中大地坐标和天文坐标本质上都是采用经度和纬度的方式来进行描述。采用经度和纬度必然面临着在椭球面上进行计算分析的考验；由于在椭球面上进行计算效率很低，会严重影响推演的效率，而平面直角坐标系本质上是局部坐标系，不能有效地支持大区域建模，存在距离、角度、面积等方面的变形。基于上述原因，本文尝试在空间直角坐标系下设计满足战术模拟的坐标系。

3.1 空间直角坐标系设计

在CGCS2000定义的参考椭球体基础上，以地球的质量中心为原点，Z轴由原点指向IERS参考极(IRP)方向，X轴由原点指向IERS参考子午线与地球赤道面的交点，Y轴与Z轴、X轴构成右手正交坐标系。参考椭球体的参数如下[13]：

地球长半轴a=6 378 137 m。

地球短半径b=6 356 752.314 14 m。

扁率f=1/298.257 222 101。

第一偏心率平方e2=0.006 694 380 022 90。

3.2 局部坐标系设计

在空间直角坐标系下能够客观、准确地描述地表现象的位置。但由于地球平均半径为6 371 km，采用32位单精度浮点数的描述精度只能达到0.5 m，而用64位双精度浮点数进行描述，则会增大数据存储量；其次，在空间直角坐标系中描述的是要素相对于地心的偏移位置，不利于分析与周围要素的位置关系；最后，现有的战术模型在建模时为了减少模型复杂度大都是在平面内对作战行动进行描述。因此，综合上述因素，本文在空间直角坐标系的基础上对局部坐标系进行设计。

如图2所示，按照一定的经差和纬差(1°×1°)将地球划分为许多单元，在每个单元的中心点处建立局部坐标系——X轴沿着该点所在纬线的切线指向正东方向，Y轴沿着该点所在经线的切线指向该点所在的北极方向，Z轴沿着该点在椭球面上的法线指向椭球体外部。这样单元内的所有要素通过转换都可以在o-xyz坐标系下进行描述。假设物体所在位置为(B,L,H),大地坐标与空间直角坐标的转换关系为f1，O-XYZ与o-xyz的偏移矩阵为A，则任意一点都可以通过f1·A转换到o-xyz坐标系下。

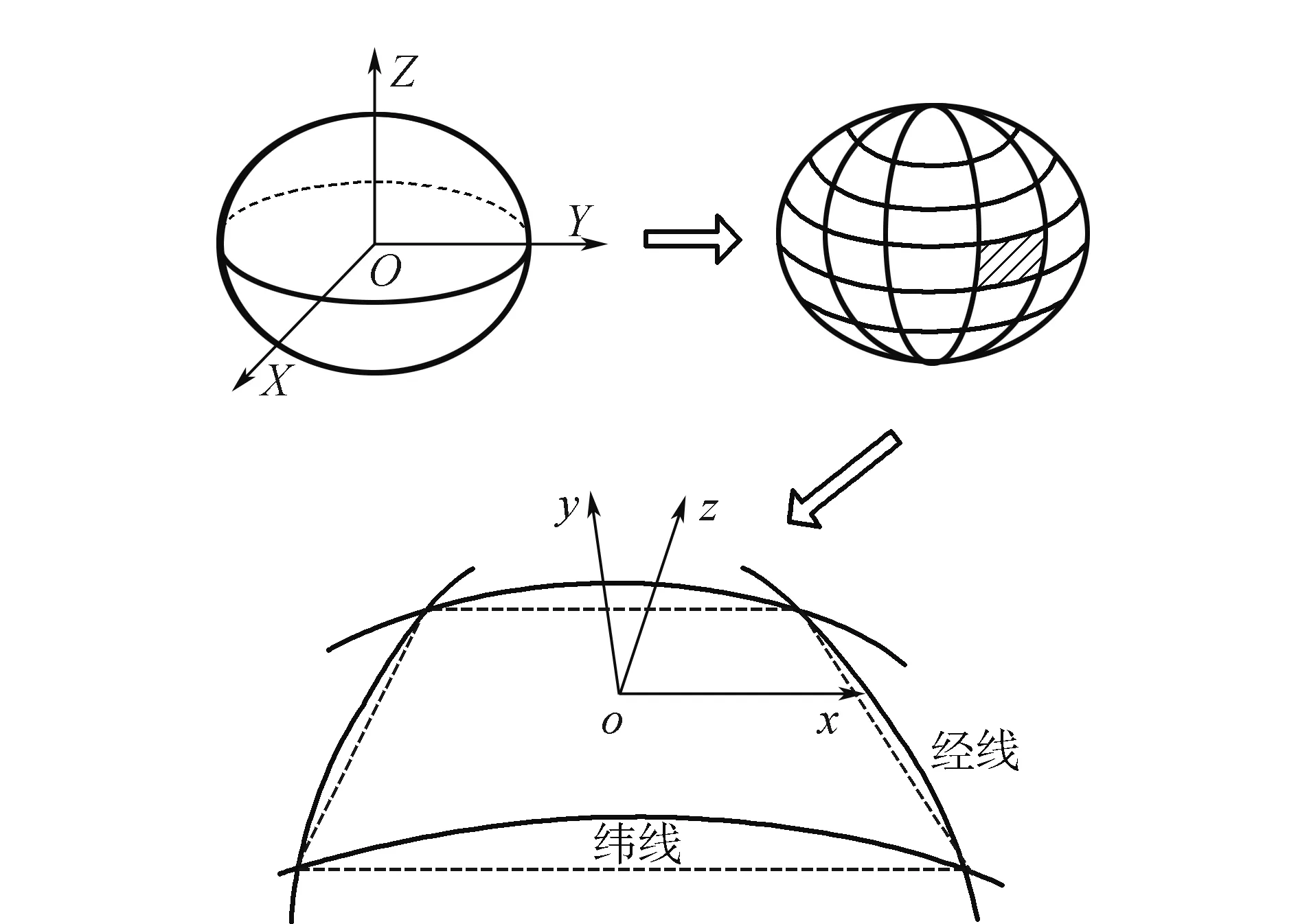
图2 坐标系设计

4 坐标系统分析

4.1 系统误差分析

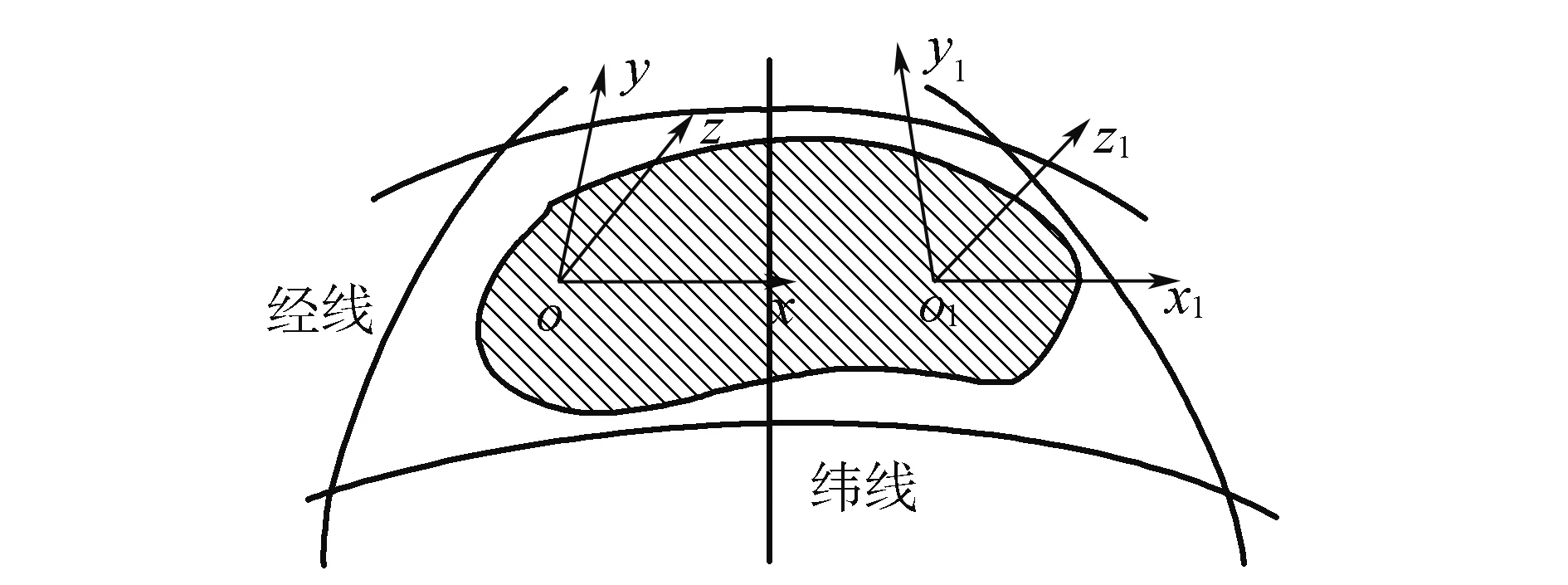
坐标系的变化必然会对高度的描述产生影响，如图3所示，地面上某一物体P在参考椭球面上的高度为h，转换到o-xyz下P在z轴的投影应该为h1(h1

图3 误差分析

4.2 系统优缺点分析

本文设计的坐标系能够有效地满足战术模拟对坐标系统的需求。该坐标系统具有以下优势：①没有进行任何投影变换，能够准确地描述要素的空间位置关系。②局部坐标系和空间直角坐标系之间的转换只是简单的矩阵旋转和平移，转换效率高。对比高斯投影坐标，本系统能够有效地弥补高斯投影的不足，能够支持任意区域、任意范围的地理环境建模。不同于高斯坐标中采用二维坐标+高程来描述要素的位置，在本坐标系下要素的任何一个点都采用三维坐标进行描述，这在一定程度上增加了数据存储量。

4.3 系统适用性分析

1)对已有作战模型的支持。现有的战术模型大都基于高斯平面对作战行动进行建模。在高斯平面中主要采用x,y,h来描述真实世界中的要素，这与x,y,z没有本质的区别。因此，在本坐标系下，现有战术模型依然能够使用。

2)对高精度计算的支持。在本坐标系下，保留了地表的曲面特征，兼顾了地球曲率对模型计算的影响，有效避免了高斯投影的不足，能够有效提高平台级模拟系统的精度。

3)对跨区域、大区域建模的支持。高斯投影无法支持跨度带的主要原因是若使用一个投影坐标系，则存在较大变形；若使用两个以上坐标系，由于不同坐标系之间的转换比较复杂，会严重影响模型计算的效率。

图4 坐标系转换

对于本坐标系而言，由于O-XYZ与o-xyz变换只是简单的矩阵旋转和平移，在模拟区域内使用不同的局部坐标系统不会影响计算效率。如图4所示，当模拟区域跨越两个单元时，分别建立局部空间直角坐标o-xyz和o1-x1y1z1，当需要跨区域计算时，无论将坐标统一到统一局部坐标系下，还是转换到空间直角坐标系下都不会影响计算效率，同时也不会影响模型计算的精度。

5 结束语

空间坐标系是对作战环境和作战行动进行描述的基础，坐标系的选择影响模型的建模精度。现代战争条件下，战术模拟对环境模型提出了更高的要求。本文针对高斯投影的不足，考虑战术模拟对坐标系的需求，设计了满足要求的坐标系。接下来，将在此基础上构建适用于战术模拟的环境模型，探讨战术环境模型的应用。

[1] 苏杰.现代作战模拟研究[M].北京:国防大学出版社,2009.

[2] 王家耀.地图学原理与方法[M].北京:科学出版社,2011:63-68.

[3] 张卫民，梁建奇，马红卫，等.陆军分队战术模拟训练系统中的坐标变换研究[J].系统仿真学报,2013，25(S1):220-221.

[4] 胡国桥.陆军分队战术训练模拟系统[J].现代实验技术，2003(1)：26-28.

[5] 徐刚.高科技条件下分队战术概论[M].北京:海潮出版社，2002.

[6] 刘非平.陆军战术模拟[M].北京:解放军出版社,2007:130-140.

[7] 李进，钱大庆，陈豪.美军大型仿真系统[J].国防科技，2009，30(1)：87-91.

[8] SMITH J E. Recent Developments in ModSAF Terrain Representation[C]. Proceedings of the 5th Conference on Computer Generated Forces and Behavioral Representation. 1995:375-379.

[9] STANZIONE T. Integrated Computer Generated Forces Terrain Database[C]. Proceedings of the 5th Conference on Computer Generated Forces and Behavioral Representation. 1995.

[10] JCATS.Terrain Generation Using TerraTools [OL].http://www.terrasim.com /brochures/products /plugins/jcats.pdf.

[11] GREEN J G.High Resolution Terrain Study[R]. Army Engineer Research and Development Center, 1996.

[12] 翟翊.现代测量学[M].北京:测绘出版社,2008:6-8.

[13] 吕志平.大地测量学基础[M].北京:解放军出版社,2005:248-250.

Coordinatesystemdesignforarmytacticssimulation

LI Kunwei, YOU Xiong,WU Zhiqiang,ZHANG Xin, TANG Fen

(School of Surveying and Mapping, Information Engineering University, Zhengzhou 450052，China)

Under the condition of joint operations, the boundaries between operation of a campaign nature and tactical action have become increasingly blurred, and the tactical action has strategic value in certain circumstance. In the field of battle simulation, tactical simulation system links with strategy or operation system providing decision support, and support platform weapon simulation. A consistent and accurate environment model is the foundation of tactical simulation system. The changes of tactical simulation system have put forward higher request to the accuracy and range of environment model in combat simulation system. Analysis is made on the disadvantage of Gauss Projection and its effects on army element tactics simulation in detail. And then this paper analyzes the demand of tactics simulation for coordinate system from the characteristics of modern team tactics. On this basis, it designs the coordinate system which can meet the requirement of team tactics simulation.

joint operations; tactics simulation; gauss projection; space rectangular coordinate

著录：李坤伟，游雄，武志强，等.面向陆军分队战术模拟的坐标系统设计[J].测绘工程，2018，27(1)：10-14.

10.19349/j.cnki.issn1006-7949.2018.01.003

2016-10-11

李坤伟(1988-)，男，博士研究生.

TP391

A

1006-7949(2018)01-0010-05

刘文霞]