基于正弦变换和背景值优化的灰色GM(1,1)模型研究

王承庆

(天津大学 管理与经济学部， 天津 300072)

基于正弦变换和背景值优化的灰色GM(1,1)模型研究

王承庆

(天津大学 管理与经济学部， 天津 300072)

对传统GM(1,1)模型进行误差分析，基于正弦变换和误差最小化原理对初始条件和背景值进行改进，建立了优化GM(1,1)模型。为了比较与传统GM(1,1)模型的优劣，选取2005—2015年我国水产品总产量数据，基于传统GM(1,1)模型和优化GM(1,1)模型分别对水产品总产量进行预测。实证研究表明：优化GM(1,1)模型在预测相对误差方面有明显改善，极大地提高了灰色模型的预测精度。

正弦变换； 背景值优化； GM(1,1)模型； 误差最小化

如果一个系统既包含已知信息又包含未知信息，且系统内各因素间存在不确定关系，则称这样的系统为灰色系统。灰色理论是一门以灰色系统为研究对象的学科，由我国学者邓聚龙教授于1982年提出。作为一种系统思想的延伸，该理论深受国内外学者欢迎，并将其广泛应用于各个领域的预测研究中。灰色预测通过分析系统内各因素间发展趋势的差异，将原始数据生成具有指数增长趋势的序列，然后建立对应的1阶常系数微分方程，利用最小二乘法原理求解，从而预测原始数据的发展趋势。最常见的灰色预测模型便是GM(1,1)模型[1-6]。

本文首先对传统GM(1,1)模型进行误差分析。如果原始数据光滑度不够，模型的误差就很难达到满意的结果。同时，传统GM(1,1)模型背景值的构造是基于梯形公式的近似面积，这就造成模型背景值大于实际背景值，也对模型的精度造成影响。针对传统GM(1,1)模型在初始条件和背景值两方面的缺陷，本文基于正弦变换和误差最小化原理对初始条件和背景值进行改进，建立了优化GM(1,1)模型，并以我国2005—2015年水产品总产量为例，研究基于正弦变换和背景值优化的GM(1,1)模型预测问题。

1 灰色GM(1,1)模型及优化

1.1 传统GM(1,1)模型

考虑到原始数据的无规律性，传统GM(1,1)模型先对原始数据序列进行累加处理，并建立1阶常系数线性微分方程，利用最小二乘法原理求解方程，以此得到原始数据的拟合曲线，再将拟合值进行累减处理，从而得到原始数据的预测值，具体建模步骤如下：

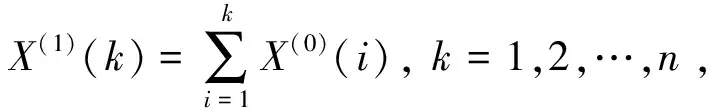
1.2 传统GM(1,1)模型的误差分析

从传统GM(1,1)模型的建模过程可以看出：发展灰数a和内生灰作用量u决定了模型的预测准确性，而原始数据的增长趋势和背景值的构造直接影响着发展灰数a和内生灰作用量u，这主要体现在以下两个方面：

1) 灰色GM(1,1)模型对具有明显指数增长趋势的原始数据有很高的模拟精度，然而在实际应用过程中，原始数据的光滑度往往有限，虽然经过累加处理能提高原始数据序列的光滑度，但还是会影响模型的准确性，使得灰色GM(1,1)模型的相对误差不能令人满意。

1.3 优化GM(1,1)模型的建立

根据上面的分析，传统GM(1,1)模型在原始数据和背景值两个方面存在缺陷，这就造成传统GM(1,1)模型的预测精度难以达到预期，本文主要基于正弦变换和误差最小化对原始数据和背景值进行优化处理。

1) 基于正弦变换的原始数据优化

鉴于实际生活中原始数据序列的光滑度有限，影响了灰色GM(1,1)模型的预测精度，目前对原始数据优化的方法主要有对数变换和正弦变换。曹昶等[7]论证了正弦变换能提高原始数据的光滑度，并在实际应用中得到满意的预测效果，因此本文采用正弦变换对原始数据进行优化，优化步骤如下:

2) 基于误差最小化的背景值优化

2 基于优化GM(1,1)模型的预测

传统GM(1,1)模型在原始数据和背景值两个方面存在改进之处，本文主要基于正弦变换和误差最小化对原始数据和背景值进行改进，建立优化GM(1,1)模型[8-13]。为了比较与传统GM(1,1)模型的优劣，选取2005—2015年期间水产品总产量数据(来自2016年国家统计年鉴)，分别采用传统GM(1,1)模型和优化GM(1,1)模型进行预测，并对两个模型的预测误差进行对比分析，结果如表1所示。

从2005年开始，我国水产品总产量始终保持着高速发展态势，传统GM(1,1)模型的预测平均误差为0.53%，说明灰色GM(1,1)模型比较适合我国水产品总产量预测。

与传统GM(1,1)模型相比，基于正弦变换和背景值优化的GM(1,1)模型的预测误差有了进一步改善，平均相对误差只有0.33%，大幅提高了灰色GM(1,1)模型的精度。 除了2012年优化 GM(1,1)模型预测值相对误差比传统GM(1,1)模型预测值相对误差较大外，其余各年的预测值相对误差均有了明显改善。因此，基于正弦变换和误差最小化的背景值优化GM(1,1)模型能进一步降低预测误差，提高灰色预测准确度，扩大了灰色GM(1,1)模型的适用范围，可以广泛用于中短期预测研究。

表1 水产品总产量预测

3 结束语

本文针对传统GM(1,1)模型在初始条件和背景值两方面的缺陷，基于正弦变换和误差最小化原理对初始条件和背景值进行优化，建立了优化GM(1,1)模型，并以我国2005—2015年水产品总产量为例，比较分析了传统GM(1,1)模型和优化GM(1,1)模型的优劣。实证结果表明：优化GM(1,1)模型能进一步降低预测误差，提高灰色预测准确度，扩大了灰色GM(1,1)模型的适用范围，可以广泛用于中短期预测研究。

[1] 胡召音.灰色理论及其应用研究[J].武汉理工大学学报(交通科学与工程版),2003,27(3):405-407.

[2] 崔杰,党耀国,刘思峰.一种新的灰色预测模型及其建模机理[J].控制与决策,2009,24(11):1702-1706.

[3] 姚天祥,刘思峰,党耀国.初始值优化的离散灰色预测模型[J].系统工程与电子技术,2009,31(10):2394-2398.

[4] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010:146-153.

[5] 刘乐,王洪国,王宝伟.基于背景值构造方法的GM(1,1)模型优化[J].统计与决策,2009,277(1):153-155.

[6] 张彬,西桂权.基于背景值和边值修正的GM(1,1)模型优化[J].系统工程理论与实践,2013,33(3):682-688.

[7] 曹昶,樊重俊,胡兆龙.基于正弦函数变换的灰色预测模型研究及其应用[J].数学杂志,2013,33(4):697-701.

[8] 徐宁,党耀国,丁松.基于误差最小化的GM(1,1)模型背景值优化方法[J].控制与决策,2015(2):283-288.

[9] 彭岩,杨卓毅.基于改进GM(1,1)模型的天津市电力消费预测研究[J].重庆理工大学学报(自然科学),2015,29(1):131-134.

[10] 邵红梅,杨建华,兰月新.基于初值修正的组合GM(1,1)模型及其应用[J].统计与决策,2015(2):89-90.

[11] 杨跃东.GM(1,1)模型的改进及其应用[D].上海：上海师范大学,2015.

[12] 于志军,杨善林,王晓佳,等.基于数据变换的GM(1,1)误差校正方法[J].系统工程理论与实践,2015(9):2339-2347.

[13] 张磊，孙长青.高阶残差修正GM(1,1)区间预测模型及其应用[J].兵器装备工程学报，2017(2):177-181.

StudyonGreyGM(1,1)ModelBasedonSineFunctionTransformationandBackgroundValueOptimization

WANG Chengqing

(College of Management and Economics, Tianjin 300072, China)

According to the error analysis of traditional GM (1,1) model, the optimized GM (1,1) model is established to improved initial condition and background value based on sine function transformation and background value optimization. In order to compare traditional GM (1,1) model to optimized GM (1,1) model, this paper chooses total output of aquatic products from 2005 to 2015 to forecast total output of aquatic products, based on traditional GM (1,1) model and optimized GM (1,1)model. The result shows that improved GM (1,1) model could greatly reduce the relative error and improve the prediction accuracy.

sine function transformation；background value optimization；GM(1，1)model；least error

2017-06-05

天津市哲学社会科学规划项目“物流企业主导下物流金融三方收益分配博弈及契约协调研究”(TJGL13-016)

王承庆(1967—)，男，海南万宁人，硕士研究生，主要从事管理科学与工程、灰色预测方面研究，E-mail:hkr3666795@163.com。

王承庆.基于正弦变换和背景值优化的灰色GM(1,1)模型研究[J].重庆理工大学学报(自然科学)，2017(12):199-202.

formatWANG Chengqing.Study on Grey GM (1,1) Model Based on Sine Function Transformation and Background Value Optimization[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):199-202.

10.3969/j.issn.1674-8425(z).2017.12.034

O175

A

1674-8425(2017)12-0199-04

(责任编辑何杰玲)