主动悬架非脆弱H∞控制器设计
马 克,米 林,谭 伟,王苏磊
(重庆理工大学 车辆工程学院, 重庆 400054)
主动悬架非脆弱H∞控制器设计
马 克,米 林,谭 伟,王苏磊
(重庆理工大学 车辆工程学院, 重庆 400054)
考虑车辆建模不确定性和执行器参数不确定性,基于2自由度1/4车辆模型设计主动悬架的非脆弱H∞控制器,使悬架加速度、悬架动扰度、轮胎形变量得到优化。非脆弱H∞控制器通过LMI(linear matrix inequality,线性矩阵不等式)算法求解,并在Matlab7.0/Simulink环境下搭建仿真模型进行仿真分析。研究结果表明:该控制器能有效改善车辆的乘坐舒适性,较好地解决平顺性与操纵稳定性之间的矛盾。
主动悬架;非脆弱H∞控制器;线性矩阵不等式
汽车悬架会对汽车整体的舒适性和安全性产生较大影响。传统的被动悬架性能只能在一定频率范围内起作用,而主动悬架能随环境的变化主动调整控制力的大小,使悬架始终处于最佳的减震状态,体现出极大的优越性。由于车辆行驶环境的不确定性,主动悬架的鲁棒控制策略受到越来越多的关注[1-2]。文献[3]采用2自由度1/4模型,基于线性矩阵不等式的方法,提出了一种考虑参数不确定性的鲁棒H2/H∞控制器设计方法。文献[4]采用7自由度整车模型,设计了基于LMI(线性矩阵不等式)算法的主动悬架H2/H∞多目标输出反馈控制器,实现了较好的平顺性和操纵稳定性。文献[5]考虑悬架系统的参数摄动与高阶未建模不确定性,基于LFT(线性分式变换)设计出μ综合控制器,仿真结果表明乘坐舒适性有很大提升。
传统的鲁棒控制往往只考虑了参数摄动和高阶未建模不确定性,在实际系统中,微处理器内存和字长的限制以及A/D、D/A转换误差等原因都可能引起控制无法准确实现,造成控制器出现摄动[6]。文献[7-8]指出:现有的鲁棒控制设计方法对控制器参数的微小摄动具有高敏感性,因此需要同时考虑系统参数和控制器的不确定性,构造出一种非脆弱的控制器,使主动悬架更稳定地运行。文献[9]基于执行机构的不确定性,为主动悬架设计出一种非脆弱H∞控制器。文献[10]为解决主动悬架执行机构的输入延迟问题,设计了一种非脆弱H∞/L2-L∞静态输出反馈控制器。文献[11]采用具有2个作动器的1/4模型,并在动力学建模过程中将人体确定振动考虑在内,应用非脆弱H∞控制策略获得较好的乘坐舒适性。
1 主动悬架动力学模型
主动悬架2自由度1/4车体悬架模型如图1所示。其中:刚性弹簧与阻尼器为悬架被动部分,作动器为悬架的主动部分,一般由液压伺服机构提供主动力u;ms为车身质量(簧载质量);mu为车轮质量(非簧载质量);ks为悬架弹簧刚度;cs为阻尼器阻尼系数;ku为轮胎刚度;xs、xu、xo分别表示车身垂直位移、轮胎垂直位移以及路面垂直位移。1/4车模型的理想动态微分方程为:

图1 1/4车体悬架模型

现将动力学模型转换成空间矩阵形式:

z(t)=C2x(t)+Du(t)

2 非脆弱H∞控制器设计
2.1 不确定系统的描述
过去30年间,H∞控制理论的应用取得了令人瞩目的成果,存在有界参数不确定性时能保证系统稳定,即具有较强的鲁棒性。文献[7]提出:控制器在作动的过程中,H∞鲁棒控制器参数也会有一定的变化,导致控制器本身出现增益扰动,这种扰动很容易导致闭环系统稳定性被破坏及性能的下降。对参数的微小改变具有高敏感性的控制器称为脆弱控制器。为使控制器具有非脆性,不仅仅要考虑系统的参数不确定性,还需考虑控制器的参数摄动。考虑如下形式的不确定系统:
(1)
其中:x(t)∈Rn表示系统状态;y(t)∈Rp表示系统的测量输出;z(t)∈Rq表示系统的控制输出;w(t)表示外界干扰;A、B1、B2、By、C1、C2、D表示维数适当的已知实常数矩阵;ΔA是未知实矩阵,反映系统的参数不确定性。将未知实矩阵的已知成分分离出来[12-14],可得到如下形式:
ΔA(t)=M1F1(t)N1
(2)
式(2)中:M1和N1是维数适当的已知矩阵;F1(t)是未知矩阵,且满足
F1(t)TF1(t)≤I, ∀t
本文旨在设计一种状态反馈非脆弱H∞控制器,具体表达式如下:
u(t)=(K+ΔK)x(t)
(3)
式中ΔK表示控制器的增益摄动。常用的ΔK构造方式有2种:加法摄动和乘法摄动,具体表达形式如下:
1) 加法摄动
ΔK=MF(t)N,F(t)TF(t)≤I
2) 乘法摄动
ΔK=MF(t)NK,F(t)TF(t)≤I
式中:M和N表示维数适当的已知矩阵;F(t)表示未知矩阵。本文选择加法摄动方式构造控制器增益摄动,即:
ΔK=M2F2(t)N2,F2(t)TF2(t)≤I
(4)
2.2 状态反馈非脆弱H∞控制器设计
为推导出状态反馈非脆弱H∞控制器的矩阵不等式,在这里介绍2条引理。
引理1 如果给定的Y、M和N是维数适当的实数矩阵,且满足:
Y+MF(t)N+NTF(t)TMT<0
对F(t)满足F(t)TF(t)≤I,那么对任意ε>0,有
Y+εMMT+ε-1NTN<0
引理2 如果Q(x)=Q(x)T,R(x)=R(x)T和S(x)是x的映射,对于LMI,
则上式LMI等效于
R(x)>0,Q(x)-S(x)R(x)-1S(x)T>0
其中R(x)表示常数。舒尔补定理把非线性不等式转化成一个线性矩阵不等式。
将本文构造的非脆弱H∞控制器代入系统状态方程中得到:
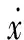
z(t)=[C2+D(K+ΔK)]x(t)
(5)
为使状态反馈非脆弱H∞控制器对不确定性ΔA(t)和ΔK能保持稳定,需要满足Hamiltonian方程[15]:

γ2wT(t)w(t)<0
(6)
其中V(x,t)表示Lyapunov函数,表达形式如下:
V(x,t)=x(t)TPx(t)
两边求导形式如下:

将式(5)代入得
P[(A+ΔA)+B1(K+ΔK)]}x(t)+
(7)
再将式(2)(4)和(7)代入式(6)得:
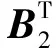
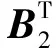
为满足H(x,w,t)<0的约束条件且[xT(t)wT(t)]≠0,
根据引理2舒尔补定理,可以将上述矩阵不等式转化为如下形式:
注:本文使用的*表示对角线转置。
现应用引理1,将上述矩阵不等式转化成如下形式:
应用引理2,将上述矩阵转化成如下形式:
对上式左乘和右乘diag{X,I,I,I,I,I,I},其中令X=P-1,KP-1=Y并且如果存在对称矩阵X>0,使上式转化成如下形式:
(8)
如果式(8)有解时,所求的状态反馈控制器为:K=YX-1,其中X∈R4×4是对称实矩阵,Y∈R1×4。
3 仿真与分析
基于本文非脆弱H∞控制器的设计过程,在Matlab7.0环境下,对采用所设计控制器的主动悬架进行仿真。车辆的参数为:ms=250 kg;mu=30 kg;ks=1×104N/m;ku=1×105N/m;cs=1 000 N·s/m。
本文的参数不确定性和控制器摄动通过LFT(线性分式变换)转换成MF(t)N形式,若要进行仿真,需要将分离出的已知矩阵进行参数设定。由本文研究可知:ΔA需要定义矩阵M1、N1;ΔK需要定义矩阵M2、N2。具体形式如下:
M1=[1 0 0 0]T
N1=[-αcs/msαcs/ms-αks/ms0]
α=0.2;M2=δ×[1 1 1 1]
N2=diag(1,1,1,1);δ=50
设置式(8)中参数ε1=ε2=5,γ=30。运用Matlab7.0中的LMI工具箱进行控制器的求解,函数lmivar,lmiterm描述矩阵不等式,函数feasp进行求解。最后求得矩阵X、Y,再根据状态反馈控制器K=YX-1,求得控制器如下:
K=105×[-0.118 6 0.033 9 -0.572 1 1.313 8]
在Matlab7.0的环境下,对采用非脆弱控制器的主动悬架进行仿真,并与被动悬架进行对比,通过Bode函数绘制悬架加速度、悬架动扰度以及轮胎变形量的幅频特性曲线,如图2~4所示。根据ISO2631标准,人体对垂直振动最敏感的频率范围为4~8 Hz。由图2可知:采用非脆弱H∞控制器的主动悬架性能在频率范围4~8 Hz内明显优于被动悬架,使乘车舒适性得到明显改善,而频率超过 10 Hz后主动悬架性能恶化明显。由图3可知:在频率小于1 Hz的情况下,采用非脆弱H∞控制器的主动悬架动扰度略有恶化,其他范围内性能略优于被动悬架。由图4可知:主动悬架的轮胎变形量在低频段处实现了部分的优化,但在高频段处却有一定的恶化。造成敏感范围优化显著、其余范围略有恶化的原因可能是加权函数选择不合适。选择加权函数协调各种性能冲突并不容易,尽管有一些指导性原则,但仍需要无数次凑试。

图2 垂向加速度幅频曲线

图3 悬架动扰度幅频曲线


图4 轮胎变形量幅频曲线

图5 垂向加速度时域曲线
由图5可知:主动悬架的垂直加速度比被动悬架有明显改善,其均方根值降低了58.1%,控制效果明显。由图6、图7可知:主动悬架动扰度比被动悬架明显减小,其均方根值降低了22.5%,但轮胎的变形量并没有明显恶化,在提高乘车舒适性的情况下,保证了车辆操纵稳定性。总的来说,与被动悬架相比,主动悬架显著降低了车身垂直加速度和悬架动扰度,同时又避免了轮胎动扰度增加过大。

图6 悬架动扰度时域曲线
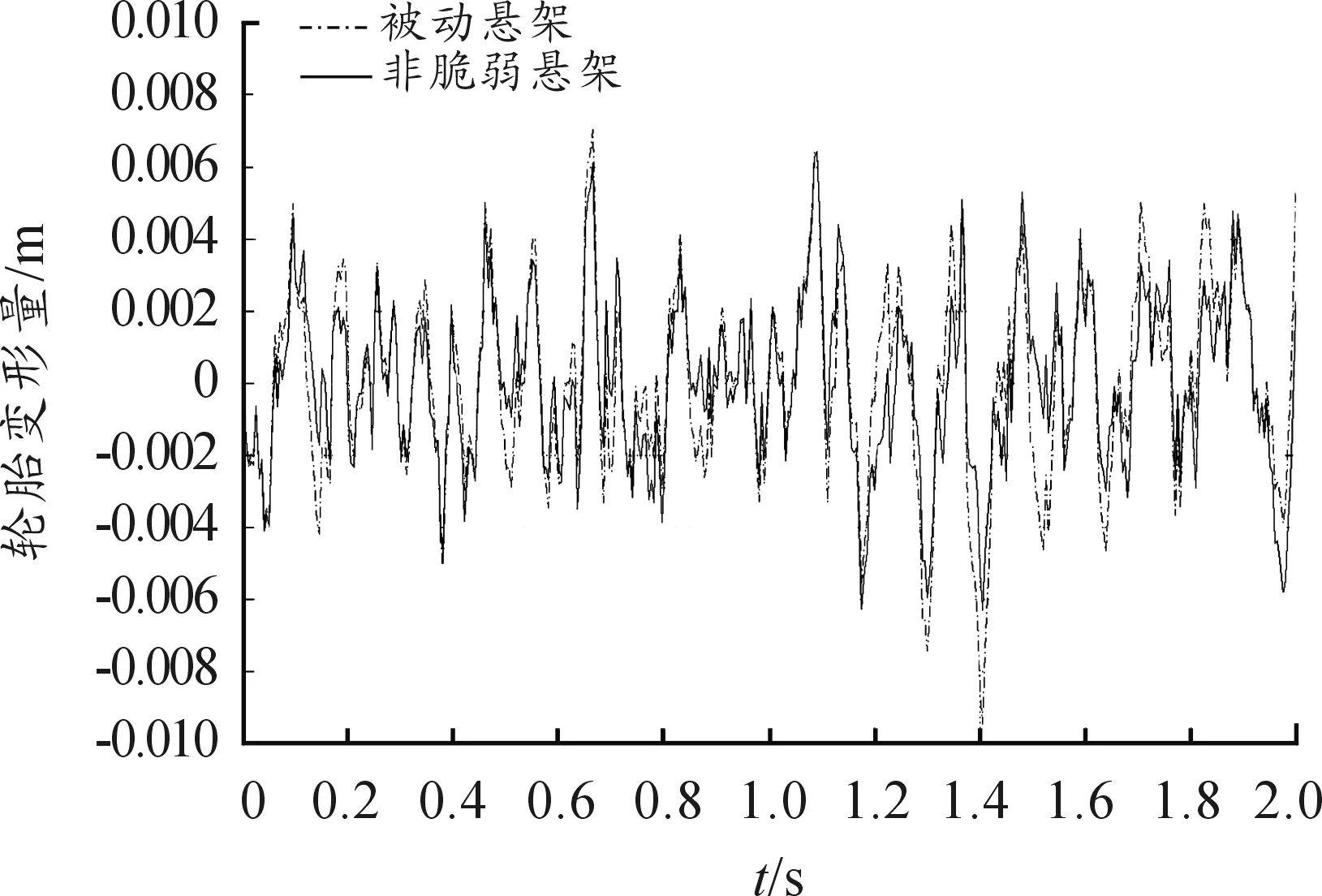
图7 轮胎变形量时域曲线
4 结束语
以车辆主动悬架的2自由度1/4模型作为受控对象,将车辆的参数不确定性和执行器不确定性列为考虑对象,设计非脆弱H∞控制器,并通过线性矩阵不等式进行求解。仿真结果证明设计的控制器是有效的,能获得比被动悬架更优异的乘车舒适性,同时车辆的操纵稳定性也得到一定保证。
[1] 于树友,陈虹.基于滚动优化的H∞/广义H2主动悬架控制[J].吉林大学学报(工学版),2007,37(5):1164-1169.
[2] YAMASHITA M,FUJIMORI K,HAYAKAWA K,et al.Application ofH∞,control to active suspension systems[J].Automatica,1994,30(11):1717-1729.
[3] 宋刚,林家浩,吴志刚.考虑参数不确定性的主动悬架鲁棒H2/H∞混合控制[J].动力学与控制学报,2008,6(2):156-164.
[4] 李以农,郑玲,罗铭刚,等.汽车主动悬架H2/H∞多目标控制线性矩阵不等式方法[J].重庆大学学报,2010,33(4):1-8.
[5] 张国光,张勇超,喻凡.车辆电动悬架的混合不确定建模与μ综合控制器设计[J].汽车工程,2012,34(12):1100-1106.
[6] 刘树博,赵丁选,尚涛.主动悬架非脆弱H2/广义H2静态输出反馈最优控制[J].四川大学学报(工程科学版),2011,43(1):240-246.
[7] KEEL L H,BHATTACHARYYA S P.Robust,fragile or optimal?[J].Automatic Control IEEE Transactions on,1997,42(8):1098-1105.
[8] DORATO P.Non-fragile controller design:an overview[C]//American Control Conference.USA:[s.n.],1998:2829-2831.
[9] LI H,LIU H,HAND S,et al.Non-fragileH∞control for half-vehicle active suspension systems with actuator uncertainties[J].Journal of Vibration & Control,2013,19(19):560-575.
[10] KONG Y,ZHAO D,YANG B,et al.Non-fragile multi-objective static output feedback control of vehicle active suspension with time-delay[J].Vehicle System Dyna-mics,2014,52(7):948-968.
[11] GUDARZI M,OVEISI A.Ride comfort performance of active vehicle suspension with seat actuator based on non-fragileH∞controller[J].International Review on Modelling and Simulations, 2015,8(1):90-98.
[12] 周云山,于秀敏.汽车电控系统理论与设计[M].北京:北京理工大学出版社,1999.
[13] TSAI M C,GU D W.Robust and optimal control[C]// Prentice-Hall,Inc.1997:2095.
[14] 梅生伟.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2008.
[15] DU H,KAM J L,SZE Y.Design of non-fragileHcontroller for active vehicle suspensions[J].Journal of Vibration & Control,2005,11(2):225-243.
DesignofNon-FragileH∞ControllerforActiveSuspension
MA Ke, MI Lin, TAN Wei, WANG Sulei
(Vehicle Engineering Institute, Chongqing University of Technology, Chongqing 400054, China)
It presents an approach to design the non-fragileH∞controller for active suspension system with parameter uncertainty and actuator uncertainty constraints, and a quarter-car model with active suspension system is considered. By using this controller, the sprung mass acceleration, suspension deflection and tire deflection are optimized. The non-fragileH∞controller can be obtained by solving a linear matrix inequality, and the simulation model can be built to analyze in Matlab7.0/Simulink. The results from the simulation demonstrate that the controller obtains a good performance of ride comfortable with less expense of handing stability.
active suspension; non-fragileH∞controller; linear matrix inequality
2017-09-22
重庆市科委科技支撑示范项目(cstc2014fazktjcsf6004);重庆理工大学科研启动基金资助项目(2015ZD06)
马克(1991—),男,硕士研究生,主要从事汽车零部件研究,E-mail:1586751087@qq.com。
马克,米林,谭伟,等.主动悬架非脆弱H∞控制器设计[J].重庆理工大学学报(自然科学),2017(12):15-21.
formatMA Ke, MI Lin, TAN Wei, et al.Design of Non-FragileH∞Controller for Active Suspension[J].Journal of Chongqing University of Technology(Natural Science),2017(12):15-21.
10.3969/j.issn.1674-8425(z).2017.12.003
U461.4
A
1674-8425(2017)12-0015-07
(责任编辑刘 舸)

