基于历史运行数据的电网运行状态演化特征提取

桂建忠，周毅博,王雅琼

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网河南省电力公司 郑州市供电公司，河南 郑州 450000)

基于历史运行数据的电网运行状态演化特征提取

桂建忠1，周毅博1,王雅琼2

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网河南省电力公司 郑州市供电公司，河南 郑州 450000)

了解电网运行状态的演化特征对系统安全运行具有积极的作用。针对模型仿真数据难以全周期描述电网运行状态的问题，提出基于SCADA系统高频的负荷实测数据连续长周期描述电网运行状态的新途径。首先，利用加权潮流熵表征电网运行负载水平和潮流分布状况的均衡性；其次，提出了基于圆分布法分析电网运行状态时序演化特性，进而提取其时序分布特征的方法；最后，实际电网算例结果表明，电网运行状态的演化时序具有在特定时段分布的特性，同时也验证了该方法的有效性。

SCADA；负载率；加权潮流熵；演化特征

随着电力系统规模的不断扩大，电力系统生产和传输的能量逐渐增加，其对国民经济和社会安全的影响日益突显，保证大规模电力系统安全经济运行具有重要意义[1]。大规模电力系统具有覆盖区域广阔、涵盖元件众多、运行方式复杂多变等特点，对其运行特征的提取是一项具有挑战性的课题[2-4]。

潮流是电力系统中节点电压、支路功率的稳态分布，是电力系统稳态运行状态的表征。大规模电力系统潮流受负荷变化、网络操作、发电机投切等影响，呈现出潮流分布不同的均匀程度。即在某一时段内，负荷变化不大，网络无操作，发电机没有投切，系统运行比较平稳，潮流分布变化不大；在另一时段，由于负荷的急剧变化或网络操作等原因，潮流可能会出现急剧的波动或大范围转移，导致系统中部分区域或元件面临运行风险，威胁到系统的安全运行[5-8]。故此，从时间和空间维度上掌握电网运行的全景信息，采取有效的方式表征潮流分布的不均匀程度，进而描述电网的运行状态演化过程十分必要。

电网输电线路的负载率水平可以表征各条输电线路的负载情况，可为对输电线路负载率变化的时空演变特征提取提供描述的数据基础，从而表征电网输电线路全景的运行状态。输电线路负载率的不均衡性增大，电网运行发生连锁故障反应的风险随之变高。近年来，针对电力系统自组织临界性的众多研究表明，电网输电线路潮流熵指标可以描述线路潮流分布的不均衡性。潮流熵对电网连锁故障的传播具有重要影响，是决定系统是否进入自组织临界态的重要指标之一[9]。在连锁故障临界识别的模型仿真中，研究者借助重要指标潮流熵对电网是否进入自组织临界状态进行识别与评估[10-11]。然而，与SCADA实测数据相比，仿真数据难以长期真实重现电网的实际运行状态[12-14]。同时，基于特定运行方式的仿真数据也不能实现对实际电网长期运行潮流熵进行统计分析，缺乏对电网运行状态演化的时序特征方面进行必要的描述。

本文首先采用SCADA系统记录的电网运行数据，以电网各厂站、线路实测数据为基础，进行相关负荷实测和元件负载率、电网平均负载率的计算与统计；然后，结合负载率和潮流熵对电网线路实际的运行状态进行定量表征，提出利用圆分布数据统计分析方法对电网运行状态演化的时序分布特征进行提取。实际电网算例表明，本文提出的方法能够有效提取电网运行状态演化特征的时序分布特性。

1 电网运行负载水平

电网运行平均负载率大小在一定程度上反映全网负荷水平的大小。输电线路负载率大小可以衡量该线路输送容量利用率，反映电网剩余可用输送能力的大小。

设线路i最大有功传输容量为Pimax，电网运行时输电线路i传输的有功功率为Pi，则线路i的负载率可表示为

(1)

式中：i=1、2、3、…、N；N为输电线路总数。

输电线路的最大有功传输容量Pimax主要考虑受限制于三种约束条件：热稳定约束；考虑电压损失限制约束；静态稳定约束。

在三种约束条件下输电线路的最大有功传输容量Pimax的计算公式为

(1)热稳定极限传输功率

(2)

式中：UN为输电线路i的额定电压；Imax为输电线路i持续流通最大电流值。

(2)考虑电压损失限制的极限传输功率

(3)

式中：ΔU为输电线路i允许的电压降落，一般取±5%；U为输电线路i实际运行时的电压值，kV；Q为输电线路i实际流通的无功功率，Mvar；R和X分别为输电线路i的电阻和电抗，Ω。

(3)静稳极限传输功率

(4)

式中：U1、U2分别为输电线路i线路两端实测电压，kV；X为输电线路i的电抗值，Ω；δ为输电线路i线路两端电压相角差，rad。

输电线路j时刻的平均负载率βmj可表示为

(5)

式中：j=1、2、3、…、l；lj表示j时刻电网潮流断面上输电线路的总数；l表示最大时刻点，且每两个时刻间隔为5 min。

2 基于负载水平的潮流熵

2.1 潮流熵

潮流熵是电网运行过程中定量描述线路潮流分布均衡性的指标，文献[9-11]中基于香农信息熵理论均提出潮流熵的相关概念。

设定已知的常数序列V=[V1，V2，…，Vn]，lv表示负载率βi∈(Vv，Vv+1]的线路条数，则线路负载率处于(Vv，Vv+1]的概率p(v)为

(6)

根据香农定理和公式(6)可以得出电网潮流熵为

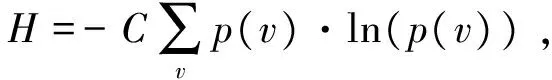
(7)

式中：C为常数，取ln10。

由公式(7)可以看出，系统潮流熵值非负且为各部分熵之和；各部分熵的序列情况不影响系统熵的大小。熵的大和小反映了系统的序列性程度低和高。映射到电网，则反映了电网输电元件负载水平的分布状态。

2.2 加权潮流熵

由公式(6)和公式(7)可知潮流熵在数学上是一种概率的表达，其对各部分熵的序列性无要求，存在不同负载率区间分布，但熵值大小一致的分布情况。该情况下的结果忽略了输电线路负载率在各个负载区间所具有的数值特征，即忽略了各区间内负载率的大小。故此需要对上述分布情况进行区分，对各部分熵值采用该区域内的平均负载率进行加权，得到加权潮流熵Hw。根据文献[11]所提的加权熵的定义，可得加权潮流熵的表示式为

(8)

式中：βm(v)为负载率βi∈(Vv，Vv+1]区间内所有线路的平均负载率；C为常数，取ln10。则有βm(v)为

(9)

3 潮流熵时间分布特征提取

圆分布法对按规定时间内获取的数据，通过三角函数变换，实现数据的线性关系计算。该方法可以分析数据所描述的现象是否在时间上具有聚集性，是否具有周期性，是否在周期内均匀分布，并且可以揭示现象出现的高峰期。

圆分布方法分析的是角度变量，故需要对本文加权潮流熵的时序进行角度转换。根据本文数据分析需要，其角度表达为

(10)

式中：αik为第Ni天的第k个量测数据；Nmax为该组分析数据的总天数。SCADA系统每隔5 min进行一次量测记录，全天共有288个量测记录时间点，且每两个记录时间点相隔5 min，则其中第k个量测数据所对应的时刻为该天的第5kmin。

圆分布法的重要参量计算公式如下：

(1)角度离散程度指标：

X=(∑Hwi·cosαik)/∑Hwi，

(11)

Y=(∑Hwi·sinαik)/∑Hwi，

(12)

(13)

(2)平均角的正弦、余弦：

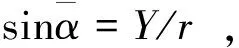
(14)

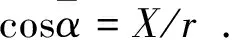
(15)

(3)圆角标准差：

(16)

4 算例分析

本文以实际电网2014年1月1日至6月30日的SCADA运行数据为数据基础，统计分析共计181天的52128个记录时刻潮流断面输电线路负载率、电网潮流熵和加权潮流熵的变化情况，分析电网运行状态的演化特性。结合电网整体负荷水平的变化，对比潮流熵和加权潮流熵表征电网运行状态演化的差异，提出了利用圆分布提取电网较高水平熵值的演化特征的方法；并且根据实际电网的运行情况，阐述了特征提取结果的合理性。

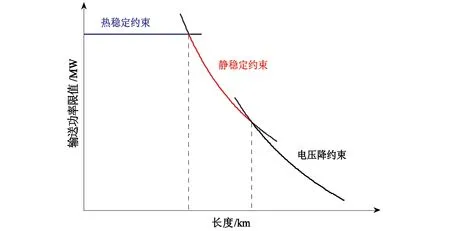
图1 输电线路输送功率极限约束曲线

4.1 输电线路功率约束极限

输电线路输送功率极限受热稳定、考虑电压损失和静态稳定极限的约束。如图1的所示，输电线路极限随输送距离长短不同，其极限约束功率随之也发生变化。

如前所述，输电线路的最大有功传输容量主要考虑受限制于热稳定约束、考虑电压损失限制约束和静态稳定约束。随着输送距离的增加其最终起作用的约束条件也随之发生变化，如图1中曲线较小值(曲线实线部分)被视为输送功率极限值。

根据输电线路型号和长度，分别计算在三种约束下的线路功率极限值。如表1所示，部分220 kV和500 kV线路的三种输送极限约束，表中加粗数值为选定的输送功率极限值。

由表1可以得出，输电线路输送功率极限随输送距离变化而发生改变；三种约束极限之间有区别，但无明确输送距离大小可以直接判定输送极限约束类型；该实际电网输电线路起作用的约束条件以热稳定极限功率和静稳极限功率为主。

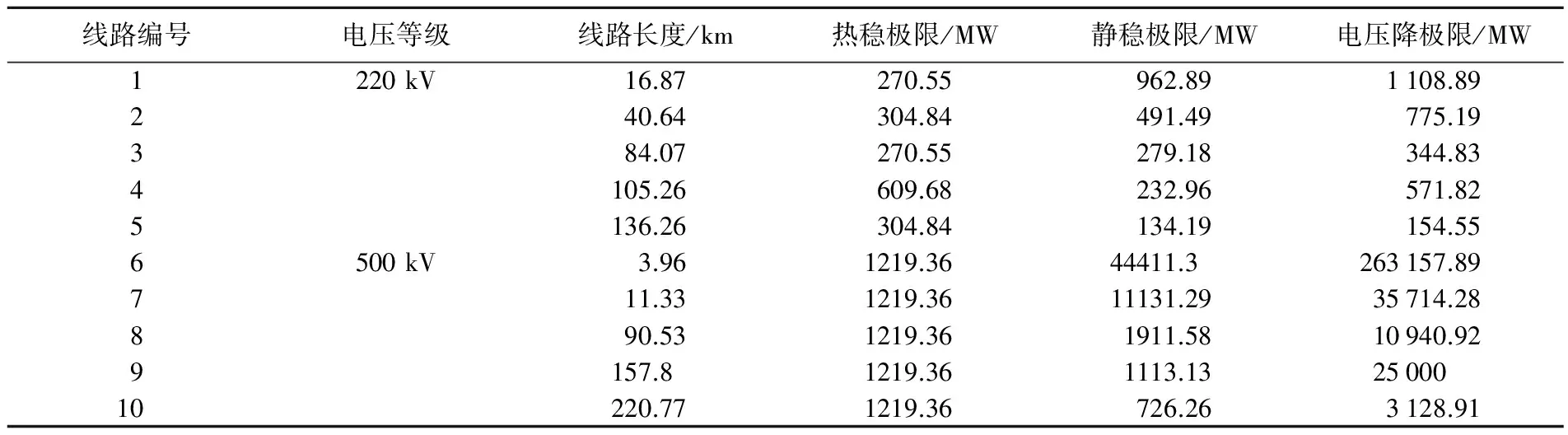
表1 输电线路输送功率极限

4.2 基于线路负载率的潮流熵与加权潮流熵

长期以来，电网平均负载水平是刻画电网运行状态自组织临界性的重要指标。但有分析表明，2005年华北电网进入自组织临界状态时的平均负载率仅为0.278。故此，基于负载率加权的潮流熵可以从一方面表示输电线路负载率分布“混乱”的情况，同时也可以反映电网的负载程度高低。

基于电网负载水平的潮流熵，在表达式上描述了电网输电线路负载率分布的有序性与否；在物理上能够识别电网运行状态的自组织临界状态的水平高低。诸多仿真分析表明，在描述电网输电线路负载情况上基于负载率加权的潮流熵在性能上要优于潮流熵。在实际电网算例中任取T1-T4时刻的潮流熵与加权潮流熵，其区分度对比结果如表2所示。

表2 电网运行潮流熵区分度对比

由表2可以得出，同一时刻电网运行状态演化水平的描述指标中，与潮流熵相比加权潮流熵之间的区别度较高。

4.3 电网运行状态日演化特征提取

电网运行状态时刻发生变化，利用加权潮流熵刻画电网运行状态的演化水平难以从时序上了解潮流熵的分布特征，而较高水平潮流熵值表征了电网运行的典型状态。对于较高水平熵值的时间分布特征提取，可以有效区分电网运行敏感时段，为运行人员了解电网运行状态提供辅助判断依据。

利用实际电网2014年1月1日-1月7日运行数据的潮流熵计算结果对每天的较高水平熵值的时间分布进行圆分布分析，确定其分布时间，如表3所示。较高熵值水平判断依据为不小于当天平均熵值2个标准差的数值。

表3 电网日演化特征第一周的分布时间

图2 较高熵值概率时间分布

由表3可以得出，每天较高水平限值大小不相同，但其分布时间分布具有明显的时段集中特征。其时间分布空值表示当天无超越限值的熵值时间分布。

为了更好的验证较高水平熵值分布时间在时间上具有相对集中的分布特征，现基于圆分布法对2014年上半年每天限值分布时间进行概率统计分析，如图2所示。各起止时段的分布概率如表4所示。

由图2可以得出，在一些特定时段，较高潮流熵值出现的概率较高。从02：40至12：05时间段，较高水平熵值分布概率持续减小；中午时段迅速回升，之后在21：30达到最小概率分布，截止到02：40逐步回升到较高概率值。这一概率分布变化与实际所在区域上半年负荷变化情况一致，即午夜01：30附近时段供暖高峰，中午13：15附近时段负荷高峰，夜间20：20附近时段各类日常负荷低谷。

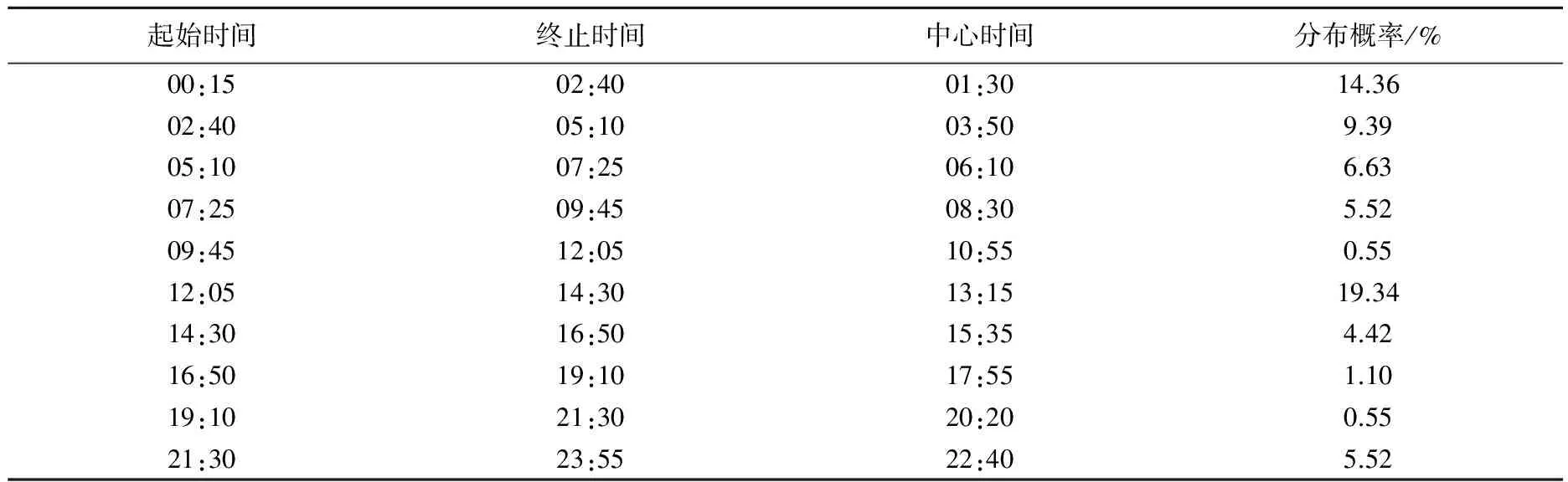
表4 2014年上半年电网日演化特征分布时间

由表4可以得出，实际电网在不同时段出现电网潮流分布不均衡现象的概率是不相同的，特别是在00：15-02：40时段和12：05-14：30时段出现的概率较高。在午夜各节点负荷都相应减小，但处于冬季受供暖后期影响，在午夜供热负荷仍处于高峰时间，且分布地区性较强，造成各输电线路负载率大小相差较大，潮流分布不均衡，故电网潮流熵值易出现较高水平；在中午时段，此时段一般均处于日常负荷高峰期，各级输电负载水平较高，电网潮流熵数值较大。

5 结 论

本文首先基于输电线路参数分析了输电线路三种输送功率极限的约束，提出了输电线路输送功率极限的一般选取规则；其次结合实际电网运行历史数据，比较了潮流熵与加权潮流熵在描述电网运行状态演化水平的区别；最后利用圆分布法提取了电网运行较高潮流熵值的时间分布特征。得到如下结论：

(1) 基于电网历史运行数据角度分析了电网自组织临界描述指标，其结果验证了加权潮流熵可以较好地描述电网运行的自组织演化水平。

(2)与仿真分析结论相比，电网长期的演化特征具有时段分布特性，即在特殊时段电网自组织性较高，电网运行相对恶劣演化的可能性较高，需要运行人员加以防范。

本文从大量电网运行数据的角度描述电网运行状态，进而提取了电网运行状态演化的时序特征，缺乏对电网运行空间特征的提取。将在下一步工作中开展相关研究。

[1] 张恒旭，刘玉田.极端冰雪灾害对电力系统运行影响的综合评估[J].中国电机工程学报，2011，31(10)：52-58.

[2] Guojiang Xiong，Dongyuan Shi，Jinfu Chen.Divisional fault diagnosis of large-scale power systems based on radial function neural network and fuzzy integral[J].Electric Power Systems Rearch，2013，105(1)：9-19.

[3] Rakibuzzaman Shah，N.Mithulananthan，R.C.Bansal.A review of key power system stability challenges for large-scale PV integration[J].Renewable and Sustainable Energy Reviews，2015，41(41)：1423-1436.

[4] 田芳，董春晖，李亚楼，等.电力系统运行及安全监控仿真系统的研究与开发[J].中国电机工程学报，2011，31(28)：80-86.

[5] A.Rouhani，A.Abur.Improving performance of dynamic state estimators under unknown load changes[C]//In：Power and Energy Society General Meeting (PES)，2013.

[6] Luo Cheng，V.Ajjarapu.Sensitivity-based efficient identification of oscillatory stability margin and damping margin using continuation of invariant subspaces[J].IEEE Transactions on Power Systems，2011，26(3)：1484-1492.

[7] 于群，郭剑波.自组织临界性与大停电事故预测[J].中国电力，2011，44(7)：21-25.

[8] 聂宏展，王叫，马方明，等.基于潮流转移识别的紧急减载控制策略研究[J].东北电力大学学报，2016，36(4)：1-6.

[9] 曹一家，王光增，曹丽华.基于潮流熵的复杂电网自组织临界态判断模型[J].电力系统自动化，2011，35(7)：1-6.

[10] 梁才，刘文颖，温志平，等.电网组织结构对其自组织临界性的影响[J].电力系统保护与控制，2010，38(20)：6-11.

[11] 刘文颖，蔡万通，张宁，等.基于联合加权熵的电网自组织临界状态演化[J].中国电机工程学报，2015，35(6)：1363-1370.

[12] 徐兴伟，穆钢，王文，等.东北电网广域动态量测系统[J].电网技术，2006，30(17)：70-73.

[13] 安军，黄桥林，刘建.基于PSAT的电力系统数值仿真模型参数校正[J].东北电力大学学报，2013，33(1/2)：1-7.

[14] 徐兴伟，穆钢，王文，等.基于SCADA和WAMS的电网仿真运行方式[J].电网技术，2006，30(19)：97-100.

FeatureExtractionofGridOperationStateEvolutionBasedonHistoricalOperatingData

GuiJianzhong1，ZhouYibo1，WangYaqiong2

(1.Electrical Engineering College，Northeast Electric Power University，Jilin Jilin 132012；2.Zhengzhou Power Supply Company,Electric Power Company of Henan,Zhengzhou Henan 450000)

It’s helpful to understand the evolution of grid operating status for the safety of power system.Due to the problems describing the full cycle operation state hardly by using the model simulation data，power load measurement can be realized based on SCADA system.The paper presents a new approach to describe the operating status of the grid based on the long period of load data measured by the high frequency of SCADA system.Firstly，the power flow entropy weighted by load rate to represent the effect of load rate and power flow distribution changes is proposed.Then，the sequence characteristics of grid operation state is analyzed to draw the time distribution of feature based on circular distribution method.Finally，the extracted features have characteristics that are distributed over a particular period of time.And the proposed method is verified effectively.

SCADA；Load rate；Weighted power flow entropy；Evolution characteristics

2017-02-28

东北电力大学研究生创新基金(Y2015003)

桂建忠(1991-),男,在读硕士研究生,主要研究方向:电力系统分析与控制.

电子邮箱：478452483@qq.com(桂建忠);zhouyiboaa@126.com(周毅博)；lovemaydayfan@163.com(王雅琼)

1005-2992(2017)06-0028-07

TP29

A