随机波浪下泰勒离散系数的时域解

郭晓梦，黄国兴，张宁川

（1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京210098；2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

随机波浪下泰勒离散系数的时域解

郭晓梦1，2，黄国兴1，2，张宁川2

（1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京210098；2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

利用Wolk提出的粒子追踪方程，通过等分频率法划分不规则波谱，利用MATLAB做粒子运动模拟计算，得到无因次化泰勒离散系数K/D随时间t变化的曲线；通过与Huang等得到的P－M谱的泰勒离散系数K/D计算结果比较证明了本计算方法的可靠性。采用该方法研究了不规则波条件下，波序列（同一谱型不同波面序列）和谱型（谱峰周期、有效波高、谱峰升高因子）对波浪离散系数的影响；计算结果表明：同一谱型不同波序列对泰勒纵向离散系数稳定值和稳定时间无影响；不规则波谱峰周期越大，纵向离散系数K/D越小，稳定时间越短；有效波高越大，纵向离散系数K/D越大，稳定时间越长；谱峰升高因子越大，泰勒离散系数K/D越大，稳定时间越长；与规则波相比，不规则波的泰勒离散系数K/D的值略小10%～30%。

泰勒离散；随机波浪；粒子追踪

目前海洋污染日益严重。准确掌握海洋中污染物的离散规律是海洋污染预防和治理的重要理论前提之一。海洋中污染物运动的主要形式有输移（advection）、扩散（diffusion）和离散（dispersion）。海洋动力环境条件下离散的最主要动力源是潮流和波浪。

关于水流为主要动力条件下污染物离散问题，起点可上溯到Taylor（1953）对管道层流中溶解物质的离散研究。之后，他又把这种方法直接推广到长直管道紊流。Fischer（1979）详尽研究了Taylor离散理论在河流中的应用，并提出估算顺直河流中一系列Taylor离散相关系数的方法。Madesen（1978）和Smith（1983）、Yasuda（1984）以长周期剪切流模型研究了潮汐流作用下的Taylor离散。

关于波浪为主要动力条件的污染物离散问题，较有代表性的研究可列举Iskandarani、Broeck、Law、Huang等人的工作，Iskandarani等（1991a，1991b）建立了波浪作用下的二维和三维输运模型；Broeck（1990）提出N层统计模型，并将Taylor机理应用于振荡剪切流中；Law（2000）基于Broeck（1990）的N层统计模型推导出行进表面波的离散系数理论公式，并针对三种典型流速分布（Stokes质量输移流、海岸垂向环流、带污染物表面Stokes质量输移流）给出了离散系数的结果。他也通过粒子随机游走数值的方法考虑了由线性波引起的粒子摆动运动的离散效应。Huang等（2011）将Taylor离散引入了以用P－M谱和Wen谱为代表的随机波浪单峰谱中，给出了泰勒纵向离散系数在随机波浪中的计算公式及结果。闫圣等也利用粒子追踪方程研究过规则波下泰勒纵向离散系数的变化情况（已录用）。但迄今为止，尚未见到考虑随机波浪下泰勒离散系数随时间变化规律等方面的研究结果的报道。时间平均的离散系数是假定垂向稳定状态泰勒离散系数只是由于平均海平面和海床之间的扩散运动，但实际波浪的其他运动形式（波面运动、波引起的振荡轨道运动等）被忽略。这样假定可以简化分析，但这不能真实反映污染物粒子在波浪下的实际运动轨迹。这种方法无法准确了解到行进波表面实时的纵向离散系数的情况，也无法预测其后续变化。

本文旨在解明随机波浪下泰勒离散系数随时间变化规律。以等分频率法划分不规则波谱，通过粒子追踪方法模拟泰勒纵向离散系数随时间的变化过程。研究了随机波浪下，波序列（同一谱型不同波面序列）和谱型（谱峰周期、有效波高、谱峰升高因子）对波浪离散系数的影响，同时比较了不规则波与规则波场中泰勒纵向离散系数的异同（离散情况达到稳定的时间和离散系数的数值变化）。

1 粒子追踪法计算随机波浪场中的泰勒纵向离散系数

粒子追踪法的原理是通过计算出流场中物质粒子的运动轨迹来确定浓度分布，根据Wolk（2003）提出的粒子追踪方程，以水底一确定点为（0，0）点，垂直海床向上为z轴正方向，沿水流方向为x轴正方向建立坐标系，以[x，z]表示水质点坐标，则水质点的欧拉方程为以下形式：

其中，u（x，z，t）、w（x，z，t）分别表示水质点x方向和z方向的速度，Dx、Dz分别为x方向和z方向的水质点分子扩散系数（本文取Dx=Dz），z1、z2为（0，1）范围内的均布随机数。

本文研究不规则波的离散情况，可以将不规则波看成由多个（理论上应该是无限多个）不同周期和不同随机初相位的余弦波叠加而成，则不规则波的波面方程，速度势方程以及x，z方向速度方程可以表示为如下形式：

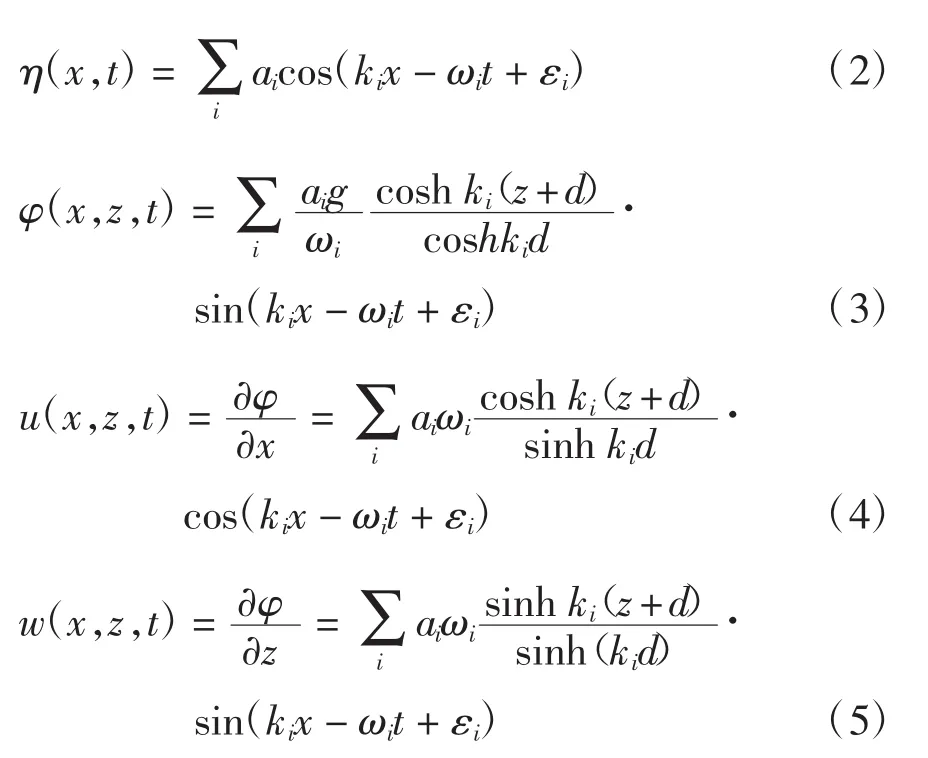
公式（2）～（5）中，ai，ki，ωi分别为第i个组成波的振幅，波数和圆频率；εi为第i个组成波的初相位，此处取在（0，2π）范围的均布随机数。

按照不规则波模拟的等分频率法（俞聿修等，2011），公式（2）～（5）中的i取1～100，将公式（4）、（5）代入（1）中逐项迭代，方程（1）中等式右端第一项采用欧拉法对时间积分，第二项采用随机行走方法处理。若粒子在自由表面边界和水底边界处随机跳出边界，则将它们通过镜像反射使其返回水域。

泰勒纵向离散系数无因次化K/D的表达形式（Law，2000）如下：

2 不规则波的泰勒纵向离散系数数值计算结果及分析

2.1 与前人结果的比较

不规则波浪场中，泰勒离散系数是随时间变化的。但随时间的推移，该离散系数将趋于稳定。Huang et al（2011）给出了不规则波条件下，以波频参量εm为参数的泰勒纵向离散系数的时间均值K/D与波离散参数Ωr关系的计算结果。为考察本文计算的泰勒离散系数结果的可靠性，将本文计算的泰勒离散系数时间变化过程在稳定区的均值与Huang et al的结果进行比较。

取不规则波频谱为PM谱（Pierson et al，1964）：

谱峰圆频率ωm与有效波高Hs满足耦合关系如下：

谱峰周期Tm=2π/ωm；波频参量εm=ω2md/g；波离散参数

计算组别参见表1。

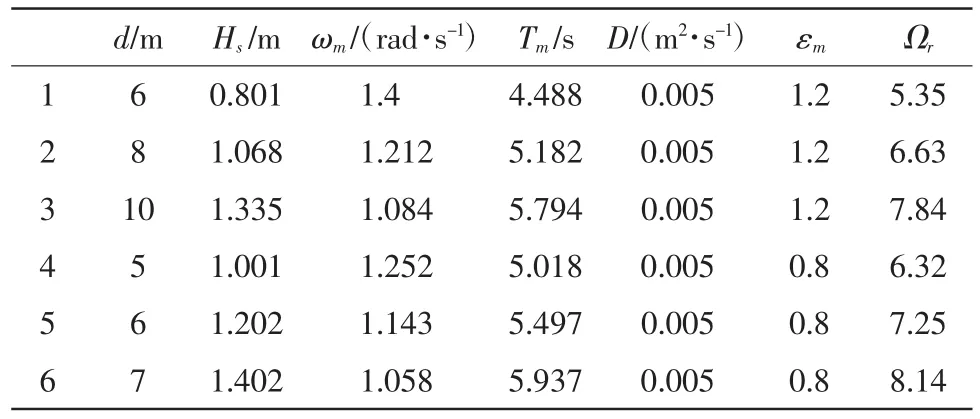
表1 PM谱计算参数表

下图1给出了一组（水深6 m，水深Hs=0.801 m，分子扩散系数D=0.005 m2/s，波频参量εm=1.2，波离散参数Ωr=5.35）泰勒纵向离散系数K/D随时间t的变化图示例。从该图可以看到K/D在t=4 h左右达到稳定，取4 h（离散系数稳定区起始点）～8 h时段K/D在时间上的平均值，可以得到该参数下K/D值稳定在20.4。将表1中各计算组别结果与Huang et al的结果的比较（其中6个点表示本文计算结果），参见图2。

图1 P-M谱泰勒离散系数K/D随时间t的变化图例

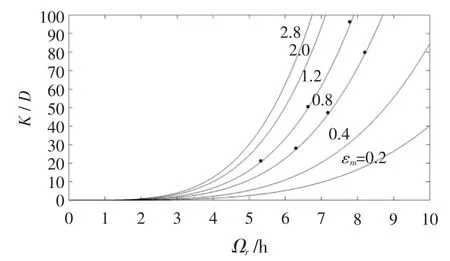
图2 Huang的K/D-Ωr图

图2可见，本文计算的泰勒离散系数时间变化过程在稳定区的均值与Huang et al的结果吻合良好。原因在于粒子整体漂移速度是由于方程（1）中等右端第一项所决定的，而第二项在统计意义上不会对平均运动产生影响。

2.2 同一波谱不同波序列的离散系数比较

理论上，同一波谱可对应无数个不同的随机波列过程。为了考察同一波谱条件下，不同的随机波列过程对泰勒纵向离散系数的影响，在此对比讨论同一波谱、两组不同的波列历时所对应的K/D随时间t变化。

取PM谱为靶谱、分子扩散系数D=0.005 m2/s，水深d=6 m；Hs=0.613 m，ωm=1.6 rad/s。选取两组不同的组成波随机初相位，得到同一波谱对应的两个随机波列过程（总时间长度为8.33 h），参见图3。

下图4给出了两组不同波列的K/D随时间t变化过程曲线，可以看出，虽然初始0～2小时时段内，K/D随时间t变化过程略有不同，但是两组不同的波列对应的K/D趋于稳定时间都为2～2.5h范围内，稳定区间5～8小时时段内K/D时间平均数值（11.9）完全一致。故可以认为同一波谱下的不同波列对K/D在趋于稳定后的影响可忽略不计。基于此，在下面的讨论中，对同一波谱，不再区分波列的影响。

图3 同一波谱对应的两组随机波面过程示例

2.3 谱峰周期对泰勒纵向离散系数的影响

对不规则波来说，谱峰周期的变化往往会对其波浪形态造成比较大的影响，因此我们考虑泰勒纵向离散系数的变化规律时要考虑谱峰周期变化的影响。

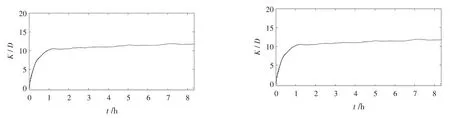
图4 两组随机波面对应的K/D随时间t变化过程示例

布氏－光易谱（B－M谱（Mitsuyasu et al，1968））是有效波高和周期联合分布的二参数谱，适用于成长阶段和充分成长的风浪，其形式如下：取B－M谱，水深为d=6m，有效波高Hs=0.8 m，分子扩散系数D=0.005 m2/s，分别取谱峰周期Tm为5 s，6 s，7 s，8 s，10 s，12 s，研究谱峰周期的变化对泰勒纵向离散系数以及离散稳定时间的影响。

由图5所示的图像可以看出谱峰周期对离散系数K/D影响显著，在本组参数下，Tm=5 s情况下的无因次化泰勒离散系数K/D为11.3，在4 h后稳定；而Tm=12 s时K/D接近0，在0.6 h后稳定。由此可以得出在水深和有效波高不变的情况下，谱峰周期Tm越大，谱峰频率ωm越小，纵向离散系数K/D越小。同时可以得出谱峰周期对离散稳定时间也有一定影响，谱峰周期越大，离散稳定时间越短之结论。

2.4 有效波高对泰勒纵向离散系数的影响

对不规则波来说，对其波浪形态影响较大的另一重要原因就是有效波高，因此我们考虑泰勒纵向离散系数的变化规律时也要考虑有效波高的影响。

以B－M谱为例，取水深为d=6 m，谱峰周期为Tm=6 s，分子扩散系数D=0.005 m2/s，分别取有效波高Hs为0.4 m，0.6 m，0.8 m，1 m，研究有效波高的变化对波浪纵向离散系数的影响以及离散稳定时间的影响。

图5 B-M谱谱峰周期变化对应的波浪离散系数K/D随时间t变化的图像

由图6所示的图像可以看出有效波高对离散系数K/D影响显著，在水深为d=6 m，谱峰周期为Tm=6 s，分子扩散系数D=0.005 m2/s，Hs=1.0 m情况下的无因次化泰勒离散系数K/D为10.3，在4h时稳定；而Hs=0.4 m时K/D接近0.3，在0.6 h后稳定。由此可以得出在水深和谱峰周期不变的情况下，有效波高Hs越大，海面波动越剧烈，泰勒纵向离散系数K/D越大。同时可以看出有效波高对泰勒纵向离散稳定时间的影响表现为有效波高越大，离散稳定时间越长。

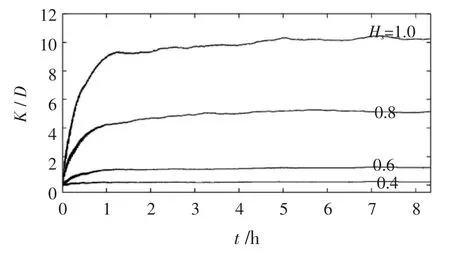
图6 B-M谱有效波高变化对应的波浪离散系数K/D随时间t变化的图像

2.5 谱峰升高因子对泰勒纵向离散系数K/D的影响

JONSWAP谱（J谱）（Hasselmann et al，1973）（是由北大西洋实测得到的有限风距谱，其形式如公式（11）所示：

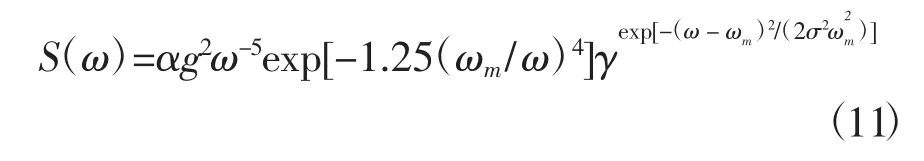
其中，α为能量尺度参数（通常取0.008 1），γ为谱峰升高因子，σ为峰形参数（当ω≤ωm时，σ=σa=0.07；当ω＞ωm时，σ=σb=0.09）。

在J谱中，除了谱峰圆频率（谱峰周期）外，谱峰升高因子对谱型的影响较大，故选取谱型升高因子γ=1～7，来研究谱峰升高因子对污染物纵向离散系数和离散稳定时间的影响。取水深d=6 m，Tm=3 s，由公式（8）可得ωm=2.09 rad/s，αg2=0.78，分子扩散系数D=0.005 m2/s。γ=1～7时，泰勒无因次化纵向离散系数K/D随时间t的变化图像如图7所示：从图中可以看到，γ越大，谱型越“尖”，无因次化泰勒离散系数K/D值越大，离散稳定时间越长。

图7 不同谱峰升高因子对纵向离散系数K/D随时间t变化的影响比较

2.6 不规则波与规则波的纵向离散系数对比

首先选取一组水深较浅时规则波和不规则波算例为例进行比较。参数选择如下：

取分子扩散系数D=0.005 m2/s，水深d=3 m；规则波取波高H=0.6 m，周期T=5 s；

不规则波谱型取为B－M谱，有效波高Hs=0.6m，谱峰周期Tm=5 s；图8为上述算例条件下不规则波与规则波的纵向离散系数随时间变化的对比图。

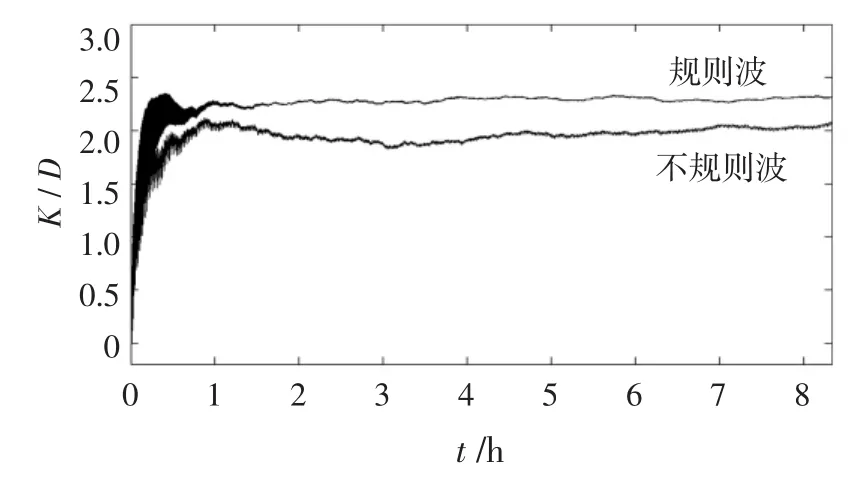
图8 一组水深较浅的不规则波与规则波的K/D随时间t对比图

图8波粒子运动稳定后的K/D值约为2.05，规则波粒子运动稳定后的K/D值约为2.3；显然相比于规则波，不规则波达到稳定的泰勒离散系数K/D小10.86%。

另取一组水深较深时，相同参数下的规则波与不规则波的泰勒离散系数作对比：

取分子扩散系数D=0.005m2/s，水深d=10m；规则波取波高H=1 m，周期T=8 s；

不规则波谱型取为B－M谱，有效波高HS=1 m，谱峰周期Tm=8 s；图9为这组算例条件下不规则波与规则波的纵向离散系数随时间变化的对比图。

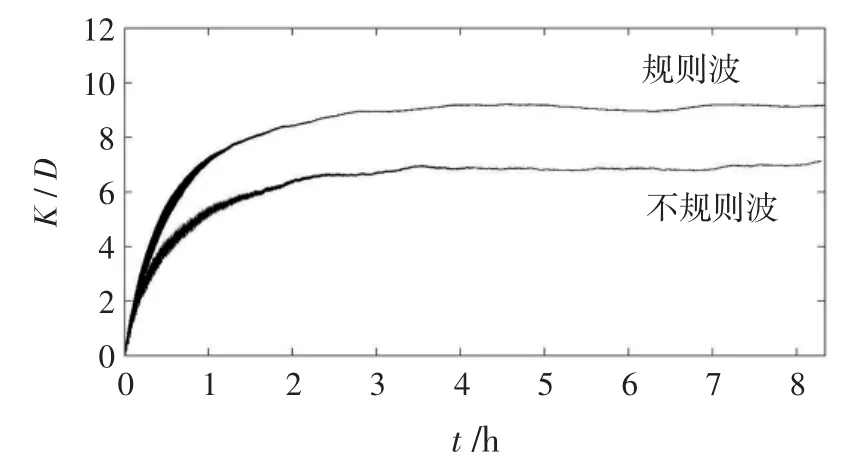
图9 另一组水深较深的不规则波与规则波的K/D随时间t对比图

从图9中可见，不规则波粒子运动稳定后的K/D值约为7.05，规则波粒子运动稳定后的K/D值约为9.2；显然相比于规则波，不规则波达到稳定的泰勒离散系数K/D小23.37%。

显然，通过以上两个算例可以得出：在水深、波高、周期相同的条件下，不规则波的泰勒纵向离散系数与规则波相比，不规则波的泰勒离散系数略小10%～30%。

3 结论

本文通过对不规则波纵向离散系数的研究，可以得出以下结论：

（1）同一谱型不同波序列对泰勒纵向离散系数稳定数值和稳定时间无影响；

（2）不规则波谱峰周期Tm越大，泰勒纵向离散系数K/D越小，稳定时间越短；有效波高Hs越大，纵向离散系数K/D越大，稳定时间越长；谱峰升高因子γ越大，泰勒离散系数K/D越大，稳定时间越长。

（3）在水深、波高、周期相同的条件下，不规则波的泰勒纵向离散系数与规则波相比，不规则波的泰勒离散系数略小10%～30%。

致谢：感谢闫圣师兄为数值模拟提供指导修改建议。

Fischer H B,1979.Mixing in inland and coastal waters.Academic press.

Hasselmann K,Barnett T P,Bouws E,et al,1973.Measurements of windwave growth and swell decay during the Joint North Sea Wave Project(JONSWAP).Deutches Hydrographisches Institut.

Huang G,Law A W K,2011.Taylor dispersion of contaminants by random waves.Journal of Engineering Mathematics,70(4):389－397.

Iskandarani M,Liu P L F,1991a.Mass－transport in 2－dimensional water－waves.Journal of Fluid Mechanics,231:395－415.

Iskandarani M,Liu P L F,1991b.Mass－transport in 3－dimensional water－waves.JournalofFluidMechanics,231:417－437.

Law A W K,2000.Taylor dispersion of contaminants due to surface waves.Journal of Hydraulic Research,38(1):41－48.

Madsen O S,1978.Mass transport in deep－water waves.Journal of Physical Oceanography,8(6):1009－1015.

Mitsuyasu H,1968.On the growth of the spectrum of wind－generated waves.2.Rep.Res.Inst.Appl.Mech,Kyushu Univ,16(55):459－482.

Pierson W J,Moskowitz L,1964.A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii.Journal of geophysical research,69(24):5181－5190.

Smith R,1983.The contraction of contaminant distributions in reversing flows.Journal of Fluid Mechanics,129(APR):137－151.

Taylor G,1953.The dispersion of soluble matter flowing through a capillary tube.Proc Math Soc London,2:196－212.

Vandenbroeck C,1990.Taylor dispersion revisited.Physica A,168(2):677－696.

Wolk F,2003.Three－dimensional Lagrangian tracer modelling in Wadden Sea areas.

Yasuda H,1984.Longitudinal dispersion of matter due to the shear effect of steady and oscillatory currents.Journal of Fluid Mechanics,148:383－403.

俞聿修，2011.随机波浪及其工程应用.大连:大连理工大学出版社.

Taylor dispersion of contaminants with time by random waves

GUO Xiao－meng1,2,HUANG Guo－xing1,2,ZHANG Ning－chuan2
（1.State Key Laboratory of Hydrology－Water Resources and Hydraulic Engineering,Nanjing Hydraulic Research Institute,Nanjing 210098,China;2.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China）

Based on Wolk's particle tracking equation,this study investigated the dimensionless Taylor dispersion K/D subject to random waves in time－domain.The Aliquots frequency method was used to simulate the random waves and the simulation of the particle motion was performed by MATLAB.The simulated results were verified by comparing to the results of Huang et al.Based on the simulated results,we discussed the effect of wave series(or different surface wave series with the same spectrum)and spectral type(including spectral peak period,significant wave height and higher spectral peak factor)on the dispersion coefficient under different random waves.The results show that different wave series with the same spectral type have insignificant effects on stable value and time of the Taylor dispersion coefficient.Also,K/D was observed to increase with shorter irregular spectral peak period,larger significant wave height and larger spectral peak factor.In addition,Taylor dispersion coefficient K/D under irregular waves is approximately 0.7～0.9 times of that under regular waves.

Taylor dispersion;random wave;particle tracking

P731.22

A

1001－6932（2017）06－0638－06

10.11840/j.issn.1001-6392.2017.06.005

2016－03－11；

2016－11－27

水文水资源与水利工程科学国家重点实验室开放研究基金（2015491311）；海岸和近海工程国家重点实验室青年学者研究基金（LY1602）。

郭晓梦（1990－），硕士研究生，主要从事海洋污染研究。电子邮箱：princessdream@163.com。

袁泽轶）