构造应力对马蹄形巷道稳定性的影响及支护设计

， ， ， ,

(1. 华北理工大学 a. 现代技术教育中心； b. 矿业工程学院， 河北 唐山 063009； 2. 大连理工大学 岩石破裂与失稳研究中心， 辽宁 大连 116000)

构造应力对马蹄形巷道稳定性的影响及支护设计

吕欣1a，武娜2，刘祥鑫1b，曹志林1b,2

(1.华北理工大学a.现代技术教育中心； b.矿业工程学院，河北唐山063009； 2.大连理工大学岩石破裂与失稳研究中心，辽宁大连116000)

根据马蹄形巷道受力后产生的变形特征，利用复变函数对马蹄形巷道进行弹塑性分析，研究构造应力的大小与方向对马蹄形巷道稳定性的影响，并针对马蹄形巷道稳定性问题，提出锚杆、锚索和混凝土喷层的联合支护方式。结果表明:构造应力大小及方向对马蹄形巷道的稳定性存在一定的影响， 其中构造应力大小显著影响马蹄形巷道变形状态， 沿最大水平主应力方向布置可改善巷道的稳定性； 联合支护后的马蹄形巷道的变形位移量约为支护前的1/4，具有良好的支护效果。

构造应力；马蹄形巷道；稳定性；联合支护

随着经济建设与科学技术的不断发展，地下空间的开发程度越来越大，并且不断走向深部[1]。对于圆形、椭圆形和直墙圆拱形巷道，已有较全面的研究，而关于马蹄形巷道的研究还有待于进一步加强。在已有的研究中，曾多次出现使用直墙圆拱断面代替马蹄形断面进行分析的案例，原因都在于建模的盲目性和困难性[2-7]。针对真正意义的马蹄形巷道，李占海等[8]和孟庆彬等[9]从侧压系数的角度分析巷道的稳定性，得出马蹄形巷道破坏是从细观单元拉伸破坏起始并沿最大主应力方向发生宏观拉伸破坏的结论；黄林华[10]通过分析应力应变云图，从二维角度考察马蹄形巷道围岩的分区破坏情况；Hui[11]考虑动载荷对马蹄形巷道稳定的影响，研究了侧向爆破作用对马蹄形巷道的动态响应。总之，马蹄形巷道稳定性研究较少见，构造应力的大小与方向是影响马蹄形巷道稳定性的2个重要因素。

随着经济建设与科学技术的不断发展，地下空间的开发程度越来越大，并且不断走向深部[1]。对于圆形、椭圆形和直墙圆拱形巷道，已有较全面的研究，而关于马蹄形巷道的研究还有待于进一步加强。在已有的研究中，曾多次出现使用直墙圆拱断面代替马蹄形断面进行分析的案例，原因都在于建模的盲目性和困难性[2-7]。针对真正意义的马蹄形巷道，李占海等[8]和孟庆彬等[9]从侧压系数的角度分析巷道的稳定性，得出马蹄形巷道破坏是从细观单元拉伸破坏起始并沿最大主应力方向发生宏观拉伸破坏的结论；黄林华[10]通过分析应力应变云图，从二维角度考察马蹄形巷道围岩的分区破坏情况；Hui[11]考虑动载荷对马蹄形巷道稳定的影响，研究了侧向爆破作用对马蹄形巷道的动态响应。总之，马蹄形巷道稳定性研究较少见，构造应力的大小与方向是影响马蹄形巷道稳定性的2个重要因素。

马蹄形断面的支护可分为2种情形：一种是原始巷道不是马蹄形巷道，支护衬砌过程中采用马蹄形断面支护，这类研究占绝大多数；另一种是原始巷道本身即为马蹄形巷道，继续对其施加马蹄形断面的支护。彭建兵等[12]通过实验研究40°斜穿地裂缝马蹄形巷道，表明巷道变形破坏具有不对称性；俞琳[13]利用Abaqus软件对马蹄形进行开挖与支护模拟，认为混凝土支护与时间呈双曲线函数关系；Yu等[14]利用FLAC软件模拟了锚杆支护对马蹄形巷道的作用；黄林华[10]考虑差异锚杆支护，也得到了较好的支护效果。从马蹄型巷道支护角度来看，主要以单一方式为主，而根据深部巷道所处的复杂地应力分布特征，单一支护方式将不再适用于深部巷道。

本文中利用复变函数对马蹄形巷道进行弹塑性受力分析，从构造应力大小和方向角度分析马蹄形巷道的稳定性问题，并针对马蹄形巷道稳定性问题，提出锚杆、锚索和混凝土喷层的联合支护方式。

1 马蹄型巷道在构造应力场中的破坏机理

1.1 基本原理

文献[15]中提出采用复变函数法整理马蹄形断面围岩应力的分析方法，思路如下：利用保角变换将不规则的图形通过一个函数映射到单位圆中，将不规则的孔口边界转变为圆形边界，而圆形断面存在解析解，这样就完成了不规则断面的应力分析。

映射函数最常用的形式是Laurent级数[15]，即

(1)

式中：R为正实数，表示孔形的大小；ζ为复数；变换系数Ck为实数；k为自然数。级数中只取几项就可以相当准确。由于推导过程十分复杂，因此直接给出Ck的6项表达式，如表1所示。这6项近似变换足以显示精确度[15]，其中R=1.678 3。

表1 映射函数的变换系数Ck(k=0,1，…，5)

1.2 复变函数法求解马蹄形巷道应力应变

1.2.1 求解过程

对于平面应力应变问题，可以根据2个解析函数来确定，

(2)

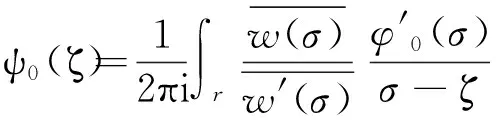
(3)

其中

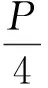
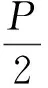
C′=0,

式中：P为垂直应力；λ为侧压系数，表示2个水平主应力的均值与垂直应力的比值；r为圆周边界；σ为转换后ζ平面上的点。

φ0(ζ)是圆外解析函数，因此可写为

(4)

式中ak为实数。

根据柯西积分公式求出φ0(ζ)表达式，

(5)

由于本文中设计的是6项近似变换，因此式(5)中各个系数的值为

(6)

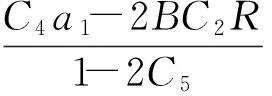
(7)

a3=-2BC3R+C5a1，

(8)

a4=-2BC4R，

(9)

a5=-2BC5R。

(10)

另外计算的有关项为

S1=-[3C5a3+2C4a2+(C3+C1C5)a1]，

(11)

S2=-(2C5a2+C4a1)，

(12)

S3=-C5a1，

(13)

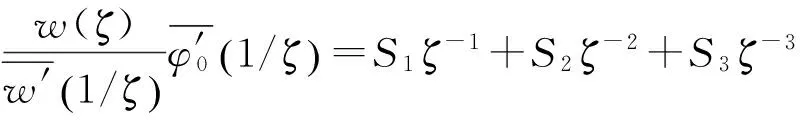
由式(2)、(3)可以求出求围岩内任意一点的应力分量。计算中用到的有关项为

w(ζ)=R(ζ+C0+C1ζ-1+C2ζ-2+C3ζ-3+

C4ζ-4+C5ζ-5)，

(14)

C4ζ4+C5ζ5)，

(15)

C4ζ4+5C5ζ4)，

(16)

w′(ζ)=R(1-(C1ζ-2+2C2ζ-3+3C3ζ-4+

4C4ζ-5+5C5ζ-6))，

(17)

w″(ζ)=R(2C1ζ-3+6C2ζ-4+12C3ζ-5+

20C4ζ-6+30C5ζ-7)，

(18)

4a4ζ-5+5a5ζ-6)，

(19)

20a4ζ-6+30a5ζ-4。

(20)

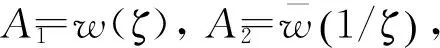
σρ+σθ=4B+4Re(A6/A4)=A11，

式中：ρ、θ为ζ平面的极坐标；σρ、σθ、τρθ为z平面正交曲线坐标系下的应力分量。

A10与A11的值可以通过MATLAB软件自动求解，令A10的实部与虚部分别表示为A12、A13。由以上参数可以最终确定出点ζ的应力分量表达式为

(21)

同时，根据弹性力学中的广义胡克定律可以将应力解转化为应变解

(22)

式中：ερ、εθ、γρθ为z平面正交曲线坐标系下的应变分量；v为泊松比；G为剪切弹性模量。

1.2.2 算例分析

对于马蹄形断面的系数，映射函数的变换系数以低马蹄形为例，计算模型参数如表2所示。

表2 算例的计算模型参数

根据式(21)、(22)编写MATLAB程序，可计算出应力与应变值，为了更规范地使用表2中的数据，事先剔除中间的巷道区域点，可以更清晰地显示等值线图。

分别将表2中的数据导入Sufer软件，通过使用Sufer软件绘制应力与应变的等值线图，如图1所示。由图可知，在巷道两帮和拱底区域出现明显的位移，在4个拱的连接处，应力集中现象表现明显。由此，在后续的数值模拟过程中可继续分析具体的影响程度，并考虑采取支护措施，以使应力分布相对均匀。

2 构造应力场中马蹄型巷道稳定性数值模拟分析

2.1 模型构建

2.1.1 模型断面尺寸选取

根据圣维南(Saint-Venant)原理可知，分布于弹性体上一小块面积(或体积)内的载荷所引起的物体中的应力，在离载荷作用区稍远的地方，基本上只与载荷的合力和合力矩有关。

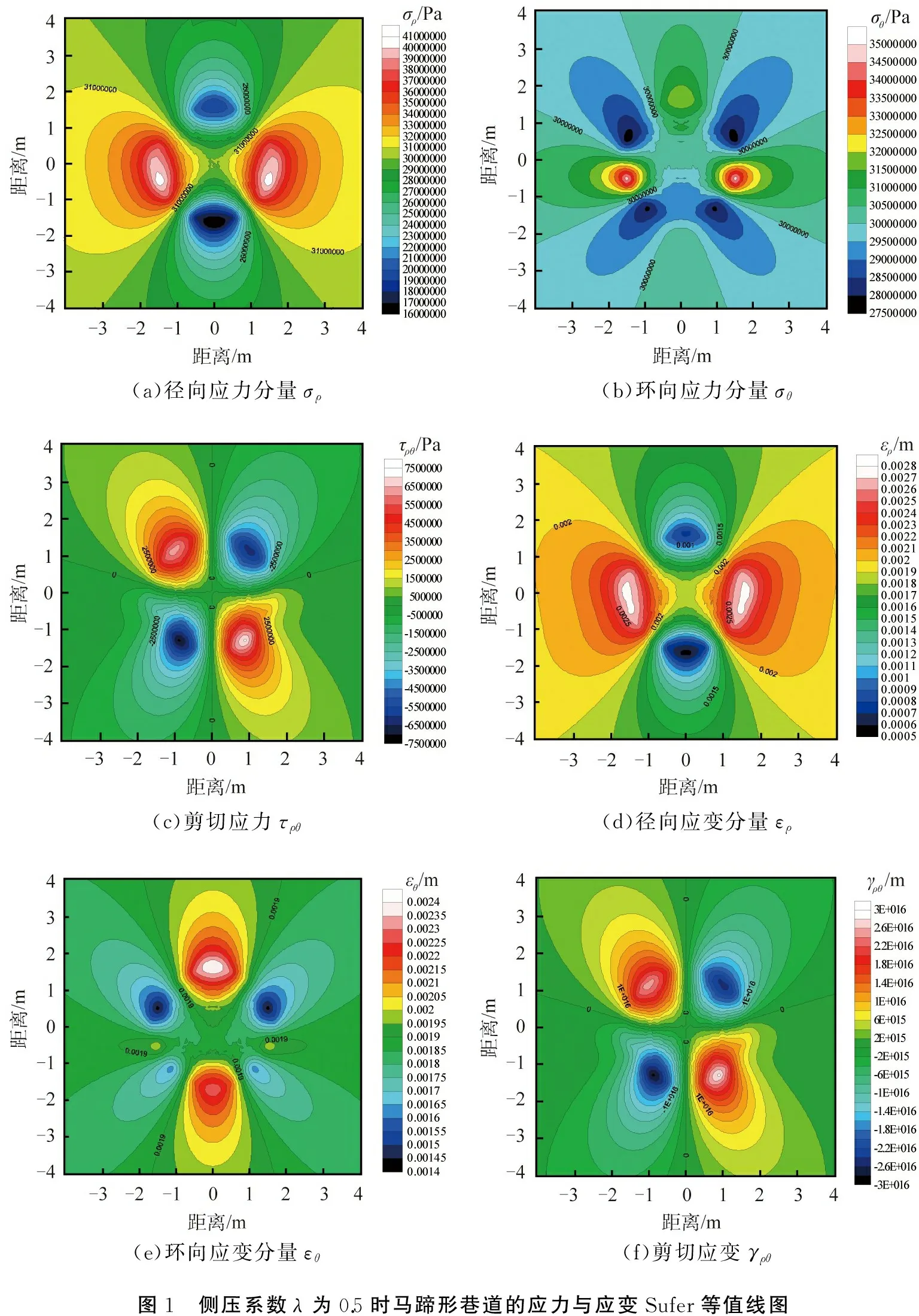
(a)径向应力分量σρ(b)环向应力分量σθ(c)剪切应力τρθ(d)径向应变分量ερ(e)环向应变分量εθ(f)剪切应变γρθ图1 侧压系数λ为0.5时马蹄形巷道的应力与应变Sufer等值线图

地下洞室开挖造成的岩体影响区域半径一般为洞室半径的3～5倍，模型的具体尺寸可根据马蹄形断面尺寸进行合理设定。本文中选择左边墙距离左边界10 m，右边墙距离右边界10 m，上边界距离拱顶的最高点10 m，下边界距离拱底的最高点10 m，开挖的马蹄形巷道半径为2 m。

2.1.2 边界条件设定

模型左、右两侧及下端设定为固定边界，上端为自由边界，由于模型自重相对地应力环境较小，因此忽略自重的梯度变化，上边界以均布超载方式加载荷载。采用FLAC 3D 5.0软件的Extrusion(挤出)建模方法，具体模型及其网格分布如图2所示。

2.2 计算参数选取

在不考虑支护问题的情况下，巷道周围的围岩力学参数如表3所示。

2.3 本构模型选取

普通土壤和岩石的力学行为，如边坡稳定和地下开挖，一般采用摩尔-库仑(Mohr-Coulomb)模型，适用于单调载荷下颗粒状材料的受力状态分析。

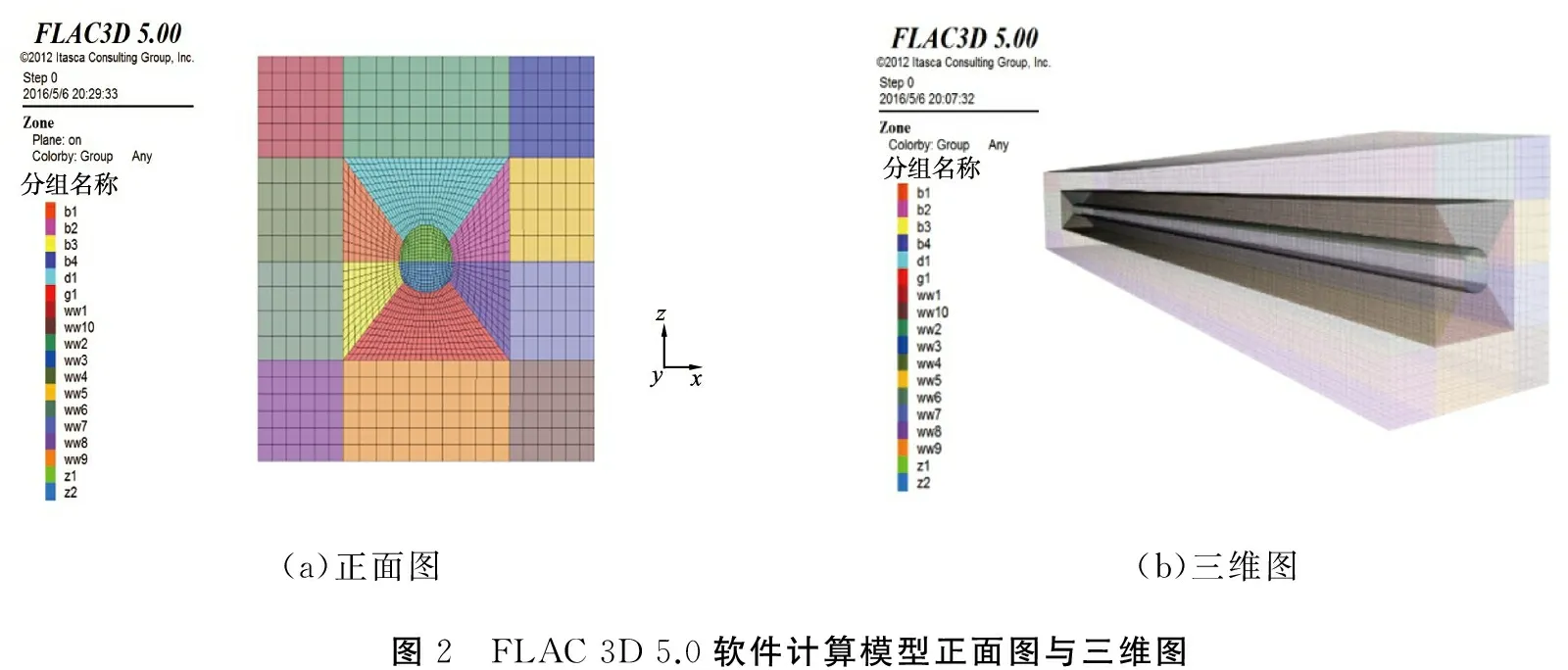
(a)正面图(b)三维图图2 FLAC3D5.0软件计算模型正面图与三维图

表3 初始计算模型参数

2.4 模拟结果分析

2.4.1 构造应力的大小对巷道稳定性的影响

构造应力的大小对巷道稳定性的影响主要从巷道位移及巷道的应力分布这2个角度来反映，取侧压系数λ=2，垂直应力P分别为10、20 MPa，通过记录巷道的水平、垂直位移，以及水平、垂直应力云图进行讨论。具体计算数据如表4所示。

表4 多状态下的计算模型参数

图3所示为FLAC 3D 5.0软件模拟构造应力的大小对巷道稳定性影响。由图可知，从纵向分析角度来看，在一定的构造应力环境中，马蹄形巷道的应力集中主要出现在4个拱的连接处，并且底拱与侧拱连接处的应力集中区域明显大于顶拱与侧拱的连接处的。从位移角度来看，应力集中区域同时表现出位移较大的情况，这一点也是支护中值得注意的地方；如果构造应力不断增大，应力集中区域更靠近巷道中心，应力值也出现相应的增大。从位移的角度来看，巷道两帮的位移明显增大，4个应力集中的连接处同样表现出位移增大的情况。由以上分析可知，马蹄形巷道4个拱的连接处应力集中现象明显，容易导致失稳，在后续的支护模拟过程中应该考虑在这4个关键点加强支护，以支护反力抵抗围岩应力。此外，在侧帮和顶底板也产生了不同程度的位移，因此在支护的过程中也不能忽略。

2.4.2 构造应力方向对巷道稳定性的影响

文献[16]中认为，全平面应变问题是在平面应变问题分析的基础上，再迭加一个面外剪切及一个单向压缩应力状态。从工程实际来看，巷道在地下的实际应力状态为三维应力状态，其受力状态如图4所示。为了研究构造应力方向对巷道稳定性的影响，通过改变最大水平应力与巷道轴向的夹角α的数值大小，实现构造应力方向对马蹄形巷道稳定性的影响研究，从巷道位移及巷道的应力分布云图分析其影响效果。

由于巷道模型的坐标系与已知的地应力不在同一个坐标系中，需要通过过渡矩阵实现三阶张量(3个应力)的坐标转换。巷道中的坐标系称为新坐标系N，而地应力坐标系称为原坐标系O，三阶张量的坐标转换式[17]为

[N]=L[O]LT，

(23)

式中：O为原坐标系的三阶张量；N为新坐标系的三阶张量；L为过渡矩阵。

根据式(23)解得新坐标系的三阶张量为

取α=0、 30、 45、 60、 90°时，分析巷道应力及位移情况。数值模拟的其他材料参数如下：泊松比为0.23，弹性模量为18.9 MPa、 内摩擦角为34°，黏聚力为10.6 MPa，地应力参数σ1、σ2、σ3分别为20、 8、 5 MPa。

(a)水平应力分布(垂直应力P=10MPa)(b)水平应力分布(垂直应力P=20MPa)(c)垂直应力分布(垂直应力P=10MPa)(d)垂直应力分布(垂直应力P=20MPa)(e)水平位移分布(垂直应力P=10MPa)(f)水平位移分布(垂直应力P=20MPa)(g)垂直位移分布(垂直应力P=10MPa)(h)垂直位移分布(垂直应力P=20MPa)图3 FLAC3D5.0软件模拟构造应力的大小对巷道稳定性影响

调用函数gp_near配合gp_xdisp、gp_zdisp编写的Fish语言统计出一条测线上的多个测点位移总和，可更准确地评估位移数据。根据以上的代码和模型参数，利用FLAC 3D 5.0软件，完成在5个角度下的水平位移和垂直位移数据的获取。对于两帮中点测线而言，其垂直位移并没有研究价值，同理，对于顶板中点测线和底板中点测线而言，其水平位移同样没有研究价值，因此本文中仅研究两帮的水平位移、顶底板的垂直位移。将FLAC 3D 5.0软件运行后的位移数据导出，使用MATLAB软件模拟构造应力的方向对巷道稳定性影响，如图5所示。需要注意的是，运行时步的前2 705步用于模型的初次平衡。图6为最大水平应力与巷道轴向的夹角是30、 45、 60、 90°时，侧帮、顶板和底板3个关键位置位移云图。由图5、6可知，当巷道轴向与最大水平应力夹角为5个不同的角度时，对于巷道顶底板和侧帮而言，其整体的变化趋势一致，均表现为位移增大，差异在于顶板和侧帮的位移表现为负向变形(分别对应顶板的冒落和侧帮的内挤)，而底板表现为正向变形(对应巷道底板的鼓起)。当巷道轴向与最大水平应力夹角由0°增大到90°时，顶板位移最大，侧帮次之，底板最小，这主要与模型本身的几何尺寸和模型4个拱的布置有关。由此可知，当巷道轴向与最大水平应力平行时，巷道关键点的位移为最小，有利于围岩的稳定，当巷道轴向与最大水平应力呈90°时，巷道两帮的位移和顶底板位移均变为最大。文献[18]中证明了当巷道轴向与最大水平应力方向的夹角小于25～30°时，对巷道稳定性的影响并不明显。

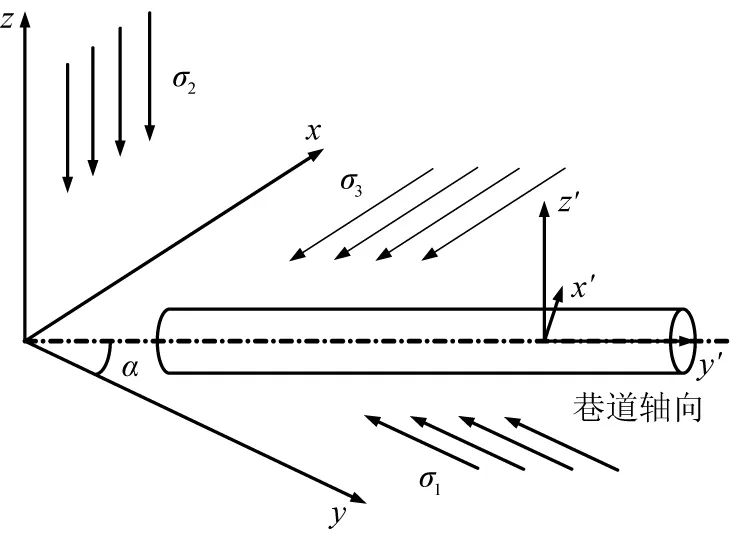
σ1、σ2、σ3—最大水平应力、中主应力、小主应力；xyz—旧坐标系；x′y′z′—新坐标系。图4 巷道的实际三轴应力状态

(a)巷道右帮水平位移

(b)巷道顶板垂直位移

(c)巷道底板垂直位移α—最大水平应力与巷道轴向的夹角。图5 FLAC 3D 5.0软件模拟构造应力的方向对巷道稳定性影响

3 基于联合支护的马蹄型巷道稳定性分析

3.1 支护方式优选

喷射混凝土支护是在围岩自稳理论基础上发展起来的一种支护方式[19]，主要起支撑、充填、隔绝和转化作用。传统锚杆支护主要基于悬吊理论、组合梁理论和组合拱理论。预应力锚索具有锚固深度大的特点，可施加预应力以实现主动支护。本文中认为对于深部巷道面临的复杂地应力环境，单一支护手段已无法满足巷道稳定性的需求，需采用以上3种方法联合支护。

3.2 支护条件下马蹄型巷道稳定性分析

针对2.1节给出的马蹄形巷道模型，对成形后的巷道进行联合支护，不考虑岩体自重，采用Mohr-Coulomb强度准则进行模拟。设计开挖长度为80 m，每次开挖2.4 m， 直至整个模型开挖结束。 每次开挖之后，由于应力的重新分布，因此在模拟时使用Shell单元及时进行喷射混凝土初衬，随后使用Cable命令模拟， 完成锚杆与锚索的安装，至此一个进尺的开挖与支护工作全部完成。以后的开挖过程与以上过程相同，直至模型贯穿。在开挖支护过程中，监测关键点的位移用于围岩的稳定性分析。

3.2.1 模型的几何尺寸

模型长度、宽度、高度分别为20、80、20 m。模型开挖的半径约为2 m，由于是马蹄形巷道，因此不存在精确半径，其中顶拱的半径为1.79 m，侧拱的半径为2.65 m，底拱的半径为2.25 m。由FLAC 3D 5.0软件生成的模型如图7所示。

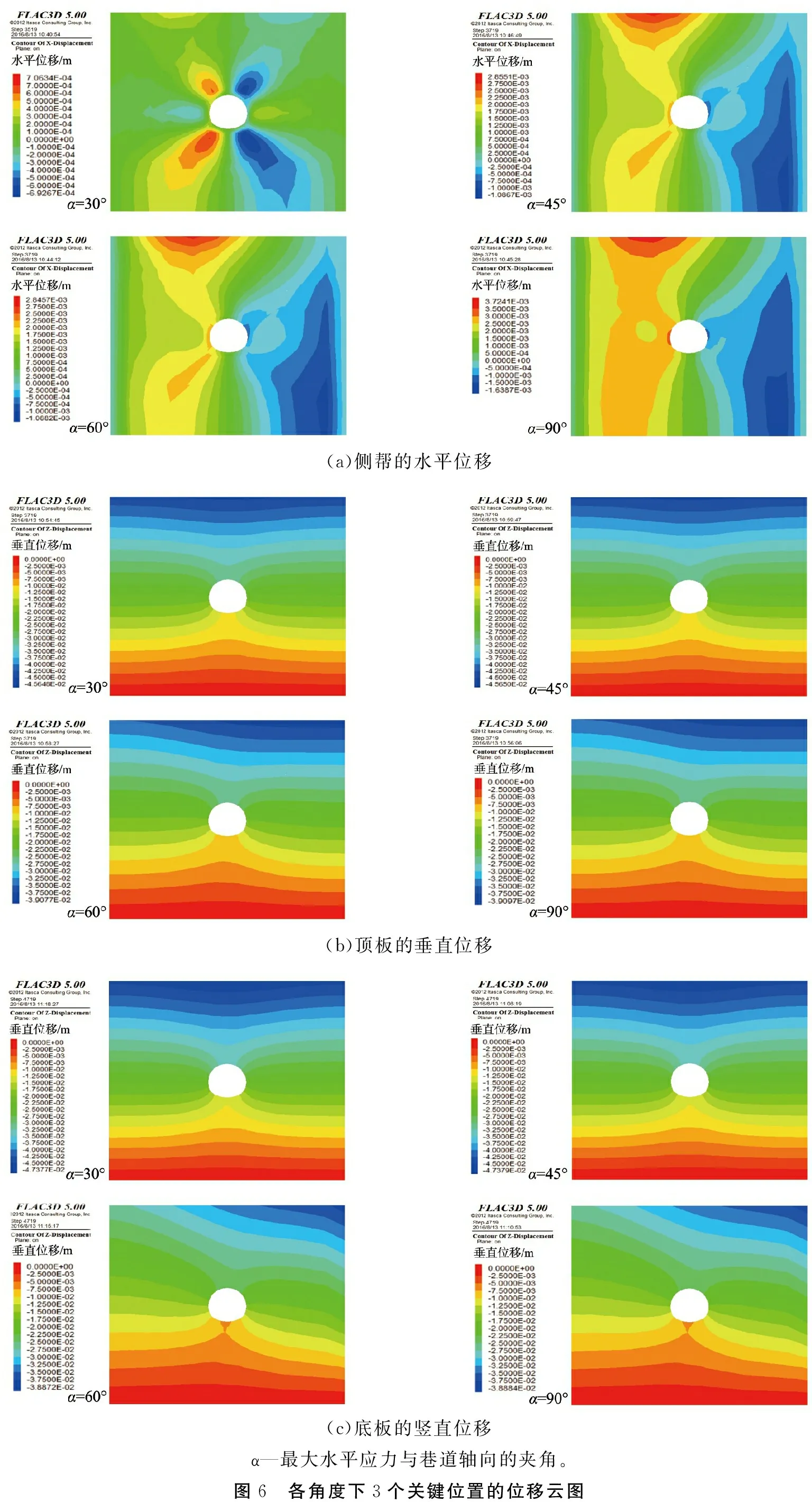
(a)侧帮的水平位移(b)顶板的垂直位移(c)底板的竖直位移α—最大水平应力与巷道轴向的夹角。图6 各角度下3个关键位置的位移云图

(a)主视图

(b)侧视图图7 FLAC 3D 5.0软件生成的数值模拟模型

3.2.2 模型岩体力学参数

模型岩体力学参数根据表3进行设定。选取的支护材料共有3种，材料参数如表5—7所示。锚杆排距为0.8 m，锚索排距为2.4 m，即在一个开挖阶段中，沿轴向位置共有3根锚杆、1根锚索，沿径向位置有11根锚杆，如图8所示，其中，主视图表示一个断面的布置，模型前倾视图表示开挖一个阶段，即2.4 m的布置。

表5 混凝土喷层材料参数

表6 锚杆材料特性

表7 锚索材料特性

3.2.3 本构模型

马蹄形巷道围岩模型采用Mohr-Coulomb模型，对于开挖断面采用Null模型。本构模型基于全局赋值。

(a)主视图

(b)模型前倾视图图8 锚杆锚索布置示意图

3.2.4 边界条件

模型的前、后、左、右以及模型底面端均固定边界，将上端设置为自由边界。

3.2.5 求解方式

对于每阶段支护使用Step命令求解，Step的步数为50，对于全局模型再使用Solve命令自动求解，设置最大不平衡力比率为10-4。

3.2.6 应力与位移的后处理及其分析

3.2.6.1 水平应力分布

为了更清晰地观测巷道内部发生的应力重分布情况，利用竖向切片法将模型切出一半，观察其内部的具体情况。水平应力的分布如图9所示。由图可知，顶拱与底拱承受了相当大的水平应力，最大应力达到64 MPa，虽然侧拱也抵抗了水平应力，但是数值只有顶底拱的1/4。此外，从分布区域的角度来看，锚杆锚索混凝土的联合支护作用使得应力分布比较均匀。

3.2.6.2 垂直应力分布

图10为巷道内部垂直应力分布云图。由图可知，垂直方向的应力主要被侧拱承担，最大数值达到60 MPa，而顶拱和底拱的贡献仅为侧拱贡献的1/4。单独从顶拱和底拱的角度分析，顶拱的应力分布区域显然小于底拱的，原因是顶拱同时存在锚杆、锚索、混凝土3种支护材料的共同维护，而底拱仅仅由其与侧拱的连接处的2根锚杆来进行维护，因此，在底拱处应力集中表现更明显。

(a)主视图

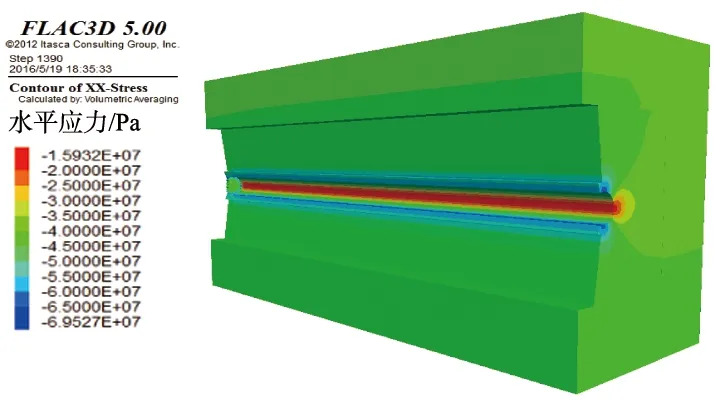
(b)内部视图图9 巷道内部水平应力分布云图

(a)主视图

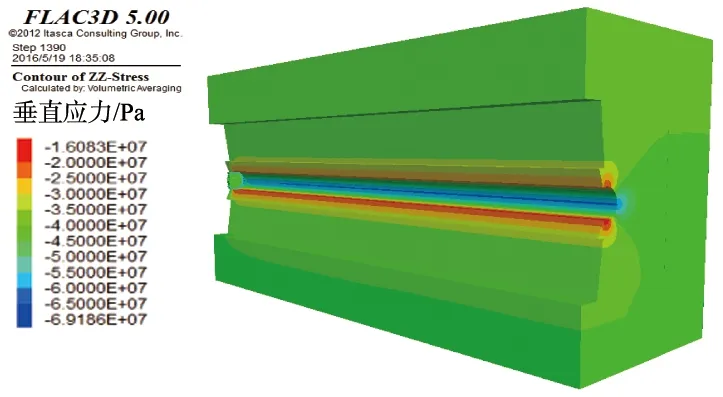
(b)内部视图图10 巷道内部垂直应力分布云图

3.2.6.3 锚杆与锚索轴向力分析

锚杆与锚索的安装在一定程度上可减小顶拱与侧拱的位移， 为了方便分析， 仅取一个阶段，锚杆与锚索自身的平均轴向力如图11所示。 由图可知， 从环向的角度来看， 每根锚杆中间段的单元应力较大， 两端应力值较小。 对于锚索而言， 也有同样的现象。 从巷道轴向的角度来看， 开挖是沿着y轴正向的， 外部的锚杆总是承受更大应力值， 因此对于远离开挖断面的外部锚杆与锚索而言， 其承受的拉力显著大于靠近开挖断面的内部锚杆与锚索， 在图中表现为锚杆与锚索中间单元的红色区域向绿色区域渐变。

(a)主视图

(b)转动方向视图图11 锚杆与锚索一个阶段的轴向力云图

3.2.6.4 混凝土喷层的法向应力分析

图12为混凝土喷层的法向应力云图。由图可知，顶拱区域的混凝土喷层承受相当大的压应力，应力值达到2.25 MPa，整体的应力数值沿着巷道中心向两侧逐渐变小，在巷道侧拱与底拱的连接处达到最小值，但是拱脚处应力集中的现象更加明显，在图中表现为红色区域狭长。

3.2.6.5 总位移场分析

巷道总位移场是评估整个模型稳定性的重要参考，本模型的总位移场如图13所示。由图可知，整体而言，位移最大值出现在拱肩和底拱处，达4.98 mm。位移从巷道中心沿着半径方向逐渐减小，在约5倍半径处接近0。

本次支护在拱与拱的连接处加强了支护的力度，例如，在顶拱与侧拱的连接处设置了锚索、锚杆和混凝土联合支护，在底拱与侧拱的连接处使用了锚杆与混凝土的联合支护，理论上应力集中应当有所改善，位移云图(图13)可以验证，这几个位置的位移相对较小。

(a)主视图

(b)转动方向视图图12 混凝土喷层的法向应力云图

(a)主视图

(b)内部视图图13 模型的总位移场云图

3.2.6.6 关键点测线位移分析

为了比较支护前、后发生的变化，根据自行编写的Fish语言，对支护前、后的模型在4个关键点进行位移的采样监测，对顶底拱提取垂直位移，对左、右帮提取水平位移，沿着开挖的方向每隔4.8 m设置一个监测点，共设置17个监测点，将其位移求和并随运行时步记录下来，其中每运行10步记录一次。 具体的数值大小与变化趋势如图14所示。 由图可知，无论是顶、底拱还是左、右两帮，各条测线的位移总是表现为支护后的位移明显小于支护前的，位移量约为支护前的1/4，说明采取联合支护后的巷道稳定性得到了显著改善。

(a)左帮

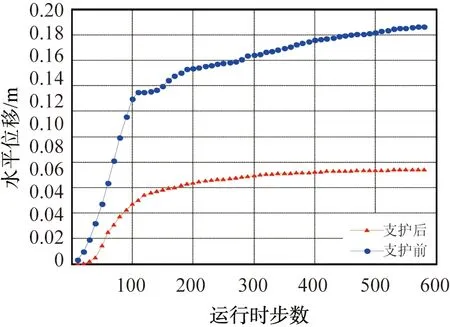
(b)右帮

(c)顶板

(d)底板图14 关键点测线位移支护前、后的对比

4 结论

1)构造应力大小及方向对马蹄形巷道的稳定性存在一定的影响，其中构造应力的大小或侧压系数可以显著影响巷道的变形状态，构造应力的方向对于巷道的影响表现在巷道布置上，沿最大水平主应力的方向布置可以改善巷道的稳定性。

2)针对工程实际中巷道的布置，在有条件的情况下，对地应力的大小与方向预先进行测量，有利于更好地把握工程地质的状况，在保证施工条件允许与安全的情况下，可以尽量沿着最大水平地应力的方向来布置巷道。

3)对于深部巷道而言，单一的支护无法满足巷道稳定性的需求，选择锚杆、锚索和混凝土喷层的联合支护方式，支护后的变形位移约为支护前的1/4，支护效果良好。

[1] 钱七虎. 非线性岩石力学的新进展——深部岩体力学的若干关键问题[C]//第八次全国岩石力学与工程学术会议论文集. 北京: 科学出版社, 2004:10-17.

[2] 左宇军, 李术才, 朱万成, 等. 深部断续节理岩体中渗流对巷道稳定性影响的数值分析[J]. 岩土力学, 2011,32(增刊2): 586-591.

[3] 郭延辉,侯克鹏.深部矿井三维地应力特征及其对巷道稳定性的影响[J].昆明理工大学学报(自然科学版), 2014, 39(2): 28-33.

[4] 李多勇. 不同侧压系数下的马蹄形洞室岩爆过程模拟[J]. 矿业工程, 2014, 12(5): 30-31.

[5] 秦源, 陈陆望. 马蹄形洞室围岩稳定性结构面倾角效应分析[J]. 合肥工业大学学报(自然科学版), 2010, 33(4): 568-571.

[6] ISLAM M R, SHINJO R. Numerical simulation of stress distributions and displacements around an entry roadway with igneous intrusion and potential sources of seam gas emission of the Barapukuria coal mine, NW Bangladesh[J]. International Journal of Coal Geology, 2009, 78(4): 249-262.

[7] TSESARSKY M, HATZOR Y H. Tunnel roof deflection in blocky rock masses as a function of joint spacing and friction a parametric study using discontinuous deformation analysis(DDA)[J]. Tunnelling and Underground Space Technology, 2006, 21(1): 29-45.

[8] 李占海, 朱万成, 冯夏庭, 等. 侧压力系数对马蹄形隧道损伤破坏的影响研究[J]. 岩土力学, 2010, 31(2): 434-441.

[9] 孟庆彬,韩立军,乔卫国,等.深部高应力软岩巷道断面形状优化设计数值模拟研究[J].采矿与安全工程学报,2012,29(5):650-656.

[10] 黄林华. 深部隧道围岩分区破裂化机理研究与数值模拟[D]. 湘潭: 湖南科技大学, 2012.

[11] HUI L. The research of dynamic response characteristics for horseshoe tunnel in the case of close side blasting[J]. Explosion and Shock Waves, 2000, 20(2): 175-181.

[12] 彭建兵, 胡志平, 门玉明, 等. 马蹄形隧道40°斜穿地裂缝的变形破坏机制试验研究[J]. 岩石力学与工程学报, 2009, 28(11): 2258-2265.

[13] 俞琳. 软岩隧道开挖与支护数值分析[D]. 大连: 大连理工大学, 2005.

[14] YU Z, KULATILAKE P H S W, JIANG F. Effect of tunnel shape and support system on stability of a tunnel in a deep coal mine in China[J]. Geotechnical and Geological Engineering, 2012, 30(2): 383-394.

[15] 吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007.

[16] 郑雨天. 井巷和钻孔周围三维应力场的简化模式[J]. 煤炭学报, 1982(4): 76-82.

[17] 徐芝纶. 弹性力学简明教程[M]. 4版. 北京:高等教育出版社, 2012.

[18] 张延新, 蔡美峰, 欧阳振华. 地应力与巷道布置关系的理论研究[J]. 岩土工程技术, 2005, 19(2): 93-97.

[19] 陈宾, 高明中. 喷射混凝土在巷道支护中的作用[J]. 煤炭技术, 2006, 25(3): 63-65.

EffectofTectonicStressonStabilityofHorse-shoeShapedRoadwayandSupportingDesign

LYUXin1a,WUNa2,LIUXiangxin1b,CAOZhilin1b,2

(1.a. Modern Technology and Education Center; b. College of Mining Engineering, North China University of Science and Technology, Tangshan 063009, China; 2. Rock Failure and Instability Research Center, Dalian University of Technology, Dalian 116000, China)

According to deformation features of the horse-shoe shaped roadway produced by sufferance forces, an elastic-plastic analysis of the horse-shoe shaped roadway was made by using complex functions. The effect of tectonic stress size and direction on the stability of horse-shoe shaped roadway was studied. The combined supporting method of anchor arm, anchor rope, and sprayed concrete layer was proposed in view of the stability of horse-shoe shaped roadway. The results show that the size and direction of tectonic stress have a certain influence on the stability of horse-shoe shaped roadway. The tectonic stress can significantly affect the deformation state of horse-shoe shaped roadway. The stability can be improved as the roadway was arranged along the maximum horizontal stress direction. The deformation displacement of the horse-shoe shaped roadway after combined supporting is about 1/4 of that before supporting, which demonstrates that the combined supporting has a good supporting effect.

tectonic stress; horse-shoe shaped roadway; stability; combined supporting

2017-02-09 < class="emphasis_bold">网络出版时间

时间：2017-12-13 16:48

国家自然科学基金项目(51604117)；河北省科技计划项目(15273908)；河北省高等学校科学研究计划项目(QN2014067)

吕欣(1979— )，女，河北唐山人。助理实验师，硕士，研究方向为采矿工程稳定性。E-mail: 850149220@qq.com。

刘祥鑫(1987— )，男，江西吉安人。讲师，博士，研究方向为采矿-岩石力学破裂机理。E-mail:liuxiangxin9@163.com。

http://kns.cnki.net/kcms/detail/37.1378.N.20171212.1637.010.html

1671-3559(2018)01-0027-12

10.13349/j.cnki.jdxbn.2018.01.005

O348.8

A

(责任编辑:王耘)