解答几何问题的几点技巧
龚柏源
解答几何问题的几点技巧
龚柏源
几何问题属于高中阶段数学一大难点,其难点在于偶然庞大的计算量与灵活多变的解题模式。几何问题很少有固定的解题模式,因此在面临几何问题时候有的学生感觉头疼。本文就解决几何问题的几点技巧做简要阐述。
在我国中学阶段,涉及到几何问题有平面几何以及立体几何两种,高中阶段主要是平面几何的计算,较少会考到平面几何的证明,立体几何则证明题与计算题都比较常见。关于解答几何问题,下面就解答几何问题的几点技巧进行阐述。
建立适当坐标系
无论是平面几何还是立体几何,解决几何问题最简单的方法就是建立坐标系,建立坐标系后的思路比起传统的证明方法来要更清晰,因此当在思考传统方法的途径上有一定问题时,不妨就将几何图形放在坐标系中,通过坐标系解决该类问题。但在建立坐标系时,要注意确定坐标系原点与几何图形的关系。一般说来,是将几何图形的某一定点作为坐标系原点,这些定点中,又以几何图形的顶点或对称点为坐标原点的最为常见。在解决实际问题时候,要根据实际问题选择对应的坐标系建立方法,不能够生搬硬套。
例如:抛物线上有两点P、Q,这两点的连线必定经过抛物线焦点F,抛物线顶点为O,焦点到顶点的距离为a,试求△OPQ的最小面积。
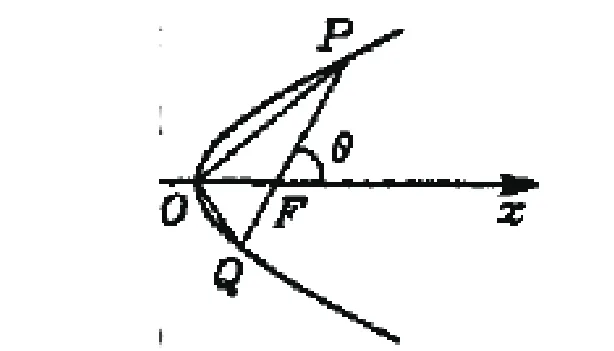
图1
解析:该题要直接解答并不容易,因此,考虑以F为坐标原点,建立坐标系。同时,假设PQ与x轴所形成的夹角为θ,如图1,因此,就可以建立以θ为未知数的抛物线方程:k∈Z)。于是,就可以用a来表示|PQ|,可以得到|PQ|=:,通过这样的表示,再从三角形的面积上入手,可以将三角形面积看作是△POF与△QOF的面积相加,或者直接利用OF与△PQO高的位置关系,都能够得到S△POQ的表达式,最终得到其表达式为通过三角函数,就能够知道当:θ=时,所求三角形的面积取得最小值,这个值为2a2。
在遇到几何问题时候,需要根据问题建立一个适当的坐标系,如果坐标系建立不够恰当,如上题,若以O点为原点建立坐标系,原本方程组就不再适合较好地用未知数:θ表示,故而在建立坐标系时,要根据实际情况建立。
注重数与形的相互转换
在高中阶段的数学几何问题中,数量关系与图形关系是解决几何问题的一个重要途径。在计算过程中,与高中阶段几何问题牵涉比较大的为参数方程、韦达定理、弦长公式等等,这些比较重要的公式定理灵活运用到几何问题当中能够在很大程度上减少计算量,提高几何问题计算的正确率。其中,参数方程的参数理解不仅对于利用数字解决最值问题有很大帮助,同时在建立坐标系、建立数学表达式等方面也很有帮助,韦达定理主要运用到交点横纵坐标的数量关系上,弦长公式通常会涉及到利用韦达定理求两点横坐标的和值或乘积。
例如:已知抛物线方程y2=2px,(p>0),有一条通过抛物线焦点的直线y=m-x与抛物线交于两点,这两点的距离为2,求p。
12以后,利用韦达定理去求y1、y2的和与积。得:y1+y2=-2p,y1y2=-p2,因此,将这两个结果与弦长的计算结果整合到一起,最终
确定定量与变量
在几何问题中,常常会有定量、定点,变量、动点,着两种相互对立的点之间一般会要求学生去寻找他们之间的关系。遇到这种题型时候,当不存在定点时,需要构造定点,便于研究动点关系。在实际解题过程中,定点对于解决问题的帮助十分重大。也就是说,在确定定点时候需要灵活将定点确定,防止定点向其他动点转换,或防止因为参考定点的确定不当,而造成最终计算量十分庞大,导致相关问题的解答出现问题。这里就立体几何的点线面确定简析。
例如:如图2,在正方体ABCD—A1B1C1D1中,正方体各边棱长为1,线段BD与AC交于点O,M在线段D1O上移动,过M做一条直线与面ACD1垂直,这条直线与平面A1B1C1D1交于点N,求N到点A的最小距离。
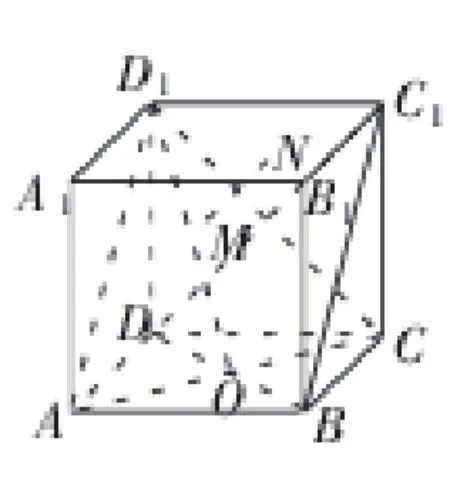
图2
解析:通过传统方法解决这一类型问题的关键在于找到与A点有最小距离的N点。如图4,连接B1D1,可以知道N点的轨迹在B1D1上,因此,在△AB1D1中,就将问题转化为A点到底边B1D1的最小距离,根据点与线距离关系可以知道,过A点做底边B1D1的垂线,这条垂线段的长度就是A点到底边距离的最小值。通过△AB1D1又能够知道,这个三角形是一个等边三角形,因此可以过A点做底边的垂线三线合一,由此,就能够得到N点与A点的最小距离
在解决这一类图形问题时候,往往都会利用到一个比较特殊的位置关系,射影,灵活应用线与平面构成的射影能够解决诸多立体几何问题。这道题的关键是将N点所可能的范围确定了出来,而其中用于确定其移动范围的是利用了平面之间的位置关系。
数学几何问题是高中阶段常考难点,它的难点往往在计算与逻辑分析上,对于计算,只要灵活运用韦达定理以及弦长公式等等,就能够很大程度缩小计算量。在逻辑分析上,确定定量与变量的关系,或建立与几何图形适应的坐标系,都能够较好对问题进行逻辑分析。
长沙市长郡中学)

