我国股价与大宗商品价格相依关系分析-基于动态copula

(浙江财经大学 浙江 绍兴 310016)

我国股价与大宗商品价格相依关系分析-基于动态copula

徐彬

(浙江财经大学浙江绍兴310016)

本文通过动态copula函数模型尽可能精确和全面地刻画我国股市和大宗商品市场间的相依关系。我国股市和大宗商品市场间表现出弱的正相依关系，并且这种相依关系具有时变特征。从动态相依程度整体变化来看，两个市场间的相依关系在不同的时间段表现出明显的阶段性特征，在2008年金融危机爆发后，相依程度水平明显上升且波动加剧，直到2014年才有所回落。因此，传统的静态相关系数分析无法有效刻画两个市场之间的动态关系，十分有必要进行动态copula函数分析。而在相依结构方面，大宗商品总指数和油脂板块指数均与我国上证指数之间表现出对称的相依结构，并且尾部相依关系较不明显。

时变 Copula；尾部相关性；AIC 准则

一、引言

随着我国金融市场的不断发展和成熟，金融市场自由化和整体化的发展趋势决定了各个金融子市场间的联系越来越紧密，因此对不同金融资产间相依关系的研究一直是实证金融界的重要议题。研究金融资产间的相依关系有助于分析金融市场间的信息传导，帮助投资者进行资产组合选择和投资风险管理。由于大宗商品价格变化的影响因素与股票大不相同，并且具有抵抗通货膨胀的作用[1-2]，越来越多的投资者们乐于把大宗商品加入到他们的资产组合中，起到分散化投资和防止极端风险的作用，因此两个市场间的相依关系成为了投资者关注的焦点。

目前国内学者的研究主要集中于我国股票市场和大宗商品市场间的溢出效应和大宗商品金融化两个方面[3]，而针对两个市场间相依关系的研究较少。特别对于我国投资者而言，为了防范极端风险事件，迫切需要清楚我国股市和大宗商品市场间的尾部相依关系以及风险管理策略。因此本文尝试填补这方面研究的空白，通过动态copula函数模型尽可能精确和全面地刻画我国股市和大宗商品市场间的相依关系，并以此为基础，构建多种投资策略下的资产组合，最后评价了各个投资策略的优化效果。

本文使用AR(1)-APGARCH(1,1)-skewed-t模型构建市场指数收益率的边缘分布模型。然后，选取了四种copula函数来捕捉两个市场间的相依结构，通过定义copula函数中参数随时间变化的自回归模型，构造了动态copula模型，探究市场间相依关系是否具有时变特征，以赤池信息量准则AIC为准则选择两个特定市场间最合适的copula函数。最后，对我国股票市场与我国大宗商品市场的动态相依度变化进行分析。

二、时变copula函数

一些学者在研究金融市场间的相依关系时，往往假设两个市场收益率间服从二元正态分布，但现实中这个假设基本上不成立。因此，如果投资者根据这个前提假设，得到两个市场间的线性相关系数，以此来配置资产组合的话，很难构建最优的投资组合，从而蒙受无谓的损失。为了更加准确地描述我国股票市场上证指数和我国大宗商品市场期货指数的相依关系，本章将使用四种copula函数来刻画两个市场间的相依关系。相比较线性相关系数，copula函数具有十分明显的优势，比如copula函数可以较为灵活地分别估计边缘分布模型和相依结构，从而大大简化了建模过程，其导出的相依关系测度是严格单调变换下的相依关系测度，比线性相关系数更适合用来刻画相依关系，并且copula函数提供了对相依关系更完整的描述，它不光描述了平均相依关系，也刻画了尾部相依关系[4]。在考察金融市场极端风险时，尾部相依关系对投资者而言是重要的考察对象。因此，本章对我国股票市场上证指数和我国大宗商品市场期货指数的实证分析将有助于我们深入认识两个市场间的相依关系。

Sklar在1959年提出了copula理论，任意两个变量的联合发布都可以分解成两个变量的边缘分布和一个连接函数，这个连接函数就是copula函数，用来描述两个变量间的相依关系。比如假设两个变量X，Y的联合分布函数为G，各自的边缘分布函数为FX和FY，那么联合分布函数G可以通过copula函数描述：G(x,y)=C(FX(x),FY(y)) 。因此可以看出，copula函数实际上起到的作用是将两个边缘分布连接在一起，构造出联合分布函数的一种函数，因此形象得被称为连接函数[5-6]。

时变 Copula 模型是指参数或者结构随着时间变化的Copula 模型。经常用来刻画资产收益率的相关关系，实际上是边缘分布函数在[0，1]区间的一种多元分布函数。时变Copula 函数与静态 Copula 函数的主要区别在于函数中的参数，时变 Copual 的参数是动态变化的，静态 Copula 中的参数是一个固定常数. 如何确定时变相依参数的演化方程是时变 Copula 的关键点，由于边缘分布模型存在 10阶滞后 ，因此 Patton 选用滞后 10 阶平均 ，提出条件Copula 时变参数模型。对于Gaussian copula函数，相依程度参数ρt的动态演化过程如下：

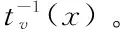
而对于Gumbel copula函数及其旋转函数Rotated gumbel copula，相关参数δt的时变过程如下所示：

其中，Λ代表转换过程Λ(x)=1+x2，用来确保δt的范围落在区间(1，∞)内。

三、实证分析

为了考察两个我国股票市场和大宗商品市场间的相依关系，本文选取了上证指数和文华商品总指数的日收盘价做为实证分析数据，通过文华财经软件获取。基于数据的可获得性，本文选取的样本区间为2004年6月3日到2017年5月28日，将两个市场的指数序列一一对应，去除所有周末和节假日的数据，并使用均值插值法补齐缺失数据，一共得到3170组数据。分别用SHCI指代上证指数，Prod指代文华商品总指数。

上证指数包含了所有在上海股票交易所交易的股票，主要由蓝筹股构成，可以很好地代表中国股票市场。而本文之所以选择使用大宗商品期货指数，而不是大宗商品现货价格，原因有三：其一，大宗商品现货种类繁多，不同品种具有异质性，不方便选取合适的市场指标；其二，本文分析股票市场和大宗商品市场相依关系的目的是为投资者配置最优资产组合提供参考，相比较特定种类的大宗商品现货，大宗商品期货指数投资产品较为成熟，投资者更为容易将其加入组合中，进行资产配置；其三，大宗商品现货价格比较容易受到短期随机扰动的影响。

本文通过将指数价格做自然对数并取一阶差分来计算资产的收益率，公式如下所示：r(i,t)=100*ln(p(i,t))/p(i,t))，其中r(i,t)代表i资产在时间t交易日的收益率，p(i,t)代表i资产在时间t交易日的指数价格。

(一)描述性统计分析

表1是上证指数和大宗商品期货指数收益率的描述性统计。从表中可以看出以下几点：1)上证指数和商品期货指数收益率的分布偏度均为负数，相比较正态分布，说明两个市场出现下跌的可能性更高；2)两个市场收益率分布的峰度都大于4，表现出尖峰厚尾的特征，这与传统认为的金融资产收益率分布特征相一致；3)两个市场收益率的J-B检验值都在5%水平上显著，结合1)、2)两点，说明两个市场指数收益率分布均不服从正态分布；4)Q(20)值和ARCH-LM统计量均在5%水平上显著，这意味着两个市场指数收益率序列均表现出自相关性和条件异方差特征。

表1 描述性统计

(二)copula函数参数估计结果分析

本章将我国股票市场和大宗商品市场间的相依关系分为两个方面，分别探究其相依结构和相依程度。按照变量间是否具有尾部相依特点，相依结构可分为线性相依结构和非线性相依结构。根据变量间的相依关系是否具有时变特征，相依程度可能为静态的或者动态的。因此首先选取了四种copula函数来捕捉两个市场间的相依结构。不同动态copula函数暗示着组合之间的相依结构也不相同，其中Gaussian copula函数和t-copula函数为均衡尾部的动态copula模型，而Gumbel copula函数及其旋转函数Rotated gumbel copula函数为非均衡尾部的动态copula模型[7]。其次，由于现实中不同金融资产间的相依关系可能具有时变特点，通过定义copula函数中参数随时间变化的演化过程，构造了动态copula模型，探究市场间相依关系是否具有时变特征。

表2给出四种copula函数在动态演化下的参数估计结果。首先，本文根据赤池信息量准则AIC来选取最合适的copula模型，从表中可以看出最能刻画SHCI-Prod组合相依关系的是动态Gaussian copula函数，说明其尾部相依性较不显著。其次，可以看到绝大部分演化方程参数Ψ1和Ψ2均为显著，所以我国股票市场上证指数与不同大宗商品市场商品期货指数之间的相依关系是具有时变特征的，也就是说静态copula模型不能完全有效刻画两个市场间的相依关系。

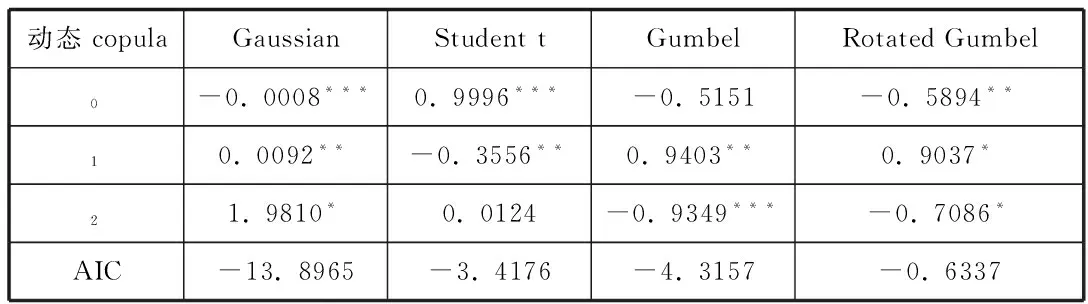
表2 动态copula函数参数估计结果

(三)动态相依程度分析

图1展示了我国股票市场上证指数与我国大宗商品市场商品总指数的动态相依程度变化。SHCI-Prod组合的动态相依程度变化通过动态Gaussian copula函数得到，动态相关系数的平均值为0.21。从图中可以看到，SHCI-Prod组合的相依程度波动较为剧烈，并且在2008有一个异常波动，其相依程度先下降，然后快速上升，虽然随后有所回落，但相依程度水平相比危机前已经上升了一个台阶。从动态相依程度整体变化来看，在不同的时间段表现出阶段性特征，2004年到2008年阶段相依程度较低，金融危机爆发后，从2008年到2014年相依程度水平明显上升，且波动幅度加剧，而到了2014年之后，相依程度大部分时间在平均水平以下。

因为SHCI-Prod组合的相依关系由动态Gaussian copula函数来描述，所以我国股票市场与我国大宗商品整体市场的收益率分布具有尾部独立性。

图1 SHCI-Prod动态平均相依程度走势图

四、结论

为了能够更加准确和全面地刻画我国股票市场和我国大宗商品市场之间的相依关系，本文通过动态copula函数模型分别刻画了两个市场间的相依结构和相依程度变化。相比较多变量GARCH模型，动态copula模型的优势在于分别构建变量各自的边缘分布模型和互相间的联合分布模型，简化了模型建立过程，并且它还可以捕捉两个市场间多种尾部相依结构，刻画非线性动态的相依程度。

我国股票市场和我国大宗商品市场之间具有较低的正向相依程度，并且表现出明显的阶段性特征，在2004年到2008年期间相依程度低且波动小，2008年金融危机爆发后，相依程度水平明显上升且波动加剧，直到2014年左右相依程度显著回落。这与我国股票市场上证指数和大宗商品市场期货指数的价格走势图的观察结果相符合，以2008年和2004年为界，在三个不同的时间段里，市场间的相依关系发生了显著变化，因此，传统的静态相关系数分析无法有效刻画两个市场之间的动态关系，十分有必要进行动态copula函数分析。据此推断，在金融危机刚爆发时，我国股票市场的暴跌还没有影响到我国大宗商品市场，但随着危机的升级，系统性的金融风险开始波及大宗商品市场，金融市场流动性收紧和投资者的悲观情绪引发大宗商品市场的下跌，这一阶段两个市场间的相依程度陡然上升，等市场情绪得到释放后，相依程度有所回落，但两个市场间的相依关系已经发生了根本性变化，相依程度在更高的水平波动。

[1]Chan，K，Treepongkaruna，S，Brooks，R，Gray，S. Asset market linkages： evidence from financial commodity and real estate assets[J.]Bank Finance，2011，35：1415-1426.

[2]Cheung，C，Miu，P. Diversi cation bene ts of commodity futures[J]. Int. Financ. Mark. Inst. Money，2010，20：451-474.

[3]金洪飞，金荦. 国际石油价格对中国股票市场的影响-基于行业数据的经验分析[J]. 金融研究，2010(2)：173-187.

[4]Patton, A. Modeling asymmetric exchange rate dependence[J]. International Economic Review, 2006, 47：527-556.

[5]张尧庭. 连接函数(Copula)技术与金融风险分析[J]. 统计研究，2002 (4)：48-51．

徐彬(1992.12-)，男，汉族，浙江省绍兴市，硕士学历，浙江财经大学，研究方向金融工程。