基于过程的融雪模型研发I——原理

高 洁

(水电水利规划设计总院，北京100120)

基于过程的融雪模型研发I
——原理

高 洁

(水电水利规划设计总院，北京100120)

研究建立了基于物理过程的能量平衡融雪模型Snow Column。模型包含能量平衡、相变、水量传递、压实和粒径变化等过程，能详细刻画雪柱在消融过程中密度剖面、温度剖面和剖面液态水含量变化。选取美国洛基山脉科罗拉多Niwot实验场006号雪坑1996年4月～6月融雪观测资料验证模型，模拟结果在合理范围内。该模型可以为进一步认识雪盖对气候变化的响应提供基础。

融雪模型; 能量平衡; Snow Column; Niwot Ridge

融雪过程模拟是寒区水文研究一个重要方面。我国是中、低纬度地区冰冻圈最发育的国家，寒区分布广泛，约占全国总面积43%[1]。我国冰雪资源丰富，稳定积雪区(积雪日数超过60天)面积约420×104km2[2]，冬季平均雪储量536×108m3[3]。对融雪过程的深入研究是寒区融雪径流模拟的基础。本文数据来源于美国科罗拉多山脉的Niwot Ridge Long-Term Ecological Research项目。

1 融雪模型

融雪模型计算方法主要包括：温度指标法和能量平衡法。温度指标法认为融雪量与温度呈一定的相关关系。即

ΔSWE=F·max(0，Ta-Tf)

(1)

式中，F为度日因子，mm℃-1d-1；Ta为日均气温，℃；Tf为临界温度，℃。

度日因子，在不同的环境条件下各有差异。它与当地坡向、发生时间有关[4]，受植被条件以及云量、降雨等天气状况的影响，并且与雪颗粒的物理属性有关，冰川积雪、高山积雪与平原积雪的消融不尽相同[5]。鉴于度日因子的不确定性，针对不同的应用流域，通常需要进行率定和验证。能量平衡法以能量输入参数作为融雪的边界条件，具有相对严格的物理基础；模型结构和参数也更加全面，便于找出误差根源[6]。模型输入主要包括短波辐射、反射辐射、上行和下行长波辐射、地热通量以及感热、潜热通量。长波辐射观测比较困难，主要是通过黑体辐射公式计算获取[5]。长波辐射、感热和潜热通量主要是发生在雪层表层，短波辐射在雪层表面50cm内仍然具有穿透性[7]。地热通量对于整个融雪期的计算非常必要，但是对于日融雪等短期融雪计算可以忽略不计。感热通量是净辐射量的40%至2倍，潜热通量与净辐射量基本位于同一量级[5]。在能量平衡融雪模型中，根据模型简化程度、雪层厚度又可以分为：单层和多层结构。单雪层模型

LfΔSWE/t=S+Lin-Lout+H+LE+G+P-
SWE(CΔTs)

(2)

式中，Lf为融解热，3.35×105J/kg；t为观测时段，s；ΔSWE为雪水的当量增量，kg/m2；S为净辐射，W/m2；Lin为雪层入射辐射，W/m2；Lout为发射长波辐射，W/m2；H为感热通量，W/m2；LE为潜热通量，W/m2；G为地热通量，W/m2；P为降水热通量，W/m2；SWE(CΔTs)为雪层的热储量变化，W/m2。

通过能量平衡项输入可推算出融化的雪水当量。但是，单雪层模型无法反映雪层内部能量和水量逐渐传递、迁移过程，由此导致径流过程呈爆发性出流，并且缺乏雪层厚度、密度、温度等变化过程参数。对于雪被较厚的寒冷及严寒地区以及下垫面条件复杂的大尺度陆面过程，建议采用多雪层分层模型。

2 模型结构

融雪模型包括单点模型和空间分布式模型。空间分布模型是在单点融雪模型的基础上，耦合空间积雪遥感资料，并集成水文汇流模块。如Snowmelt Runoff Model(SRM)[8]是以度日法为核心的单点融雪模式，考虑遥感提供的积雪高程曲线和积雪消退曲线，采用产流系数和滞时实现汇流计算的空间融雪模型；SWAT[9]、TOPMODEL[10]、新安江模型[11]、SSARR、HBV、SLURP[12]等分布式水文产汇流模型加上温度指标法或者单雪层能量平衡项的输入接口后，具备融雪径流模块功能；SWEHydro[13]以AMSR-E雪产品数据为基础，通过划分径流成分以及DEM提取地形特征实现对单点雪水当量的空间汇流计算。

本文致力于构建点尺度基于物理过程的融雪模型Snow column：首先，点尺度模型可以直接用观测资料进行直观验证；其次，点尺度模型是空间分布融雪模型的基础和核心算法；此后，可通过集成技术，与高精度遥感资料以及动力学汇流模块相耦合，逐步构建空间分布式模型。

Snow column模型包括四个主体部分：①能量平衡；②相变(质量守恒)；③水量平衡；④粒径变化和压实。对整个雪柱以一定的空间步长△z分成n层，每层包含固、液、气三相，分别以下标i，w，a表示。

3 模块说明

3.1 能量平衡

1D能量平衡模型[14]

(3)

热通量控制的上边界条件

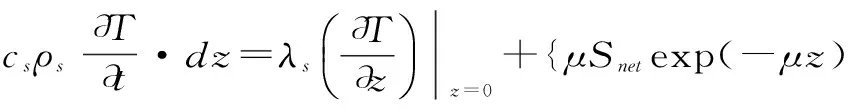
(4)

式中，Snet为净短波辐射量(入射-反射) ，W/m2；λs雪层热传导率，W/m·℃；cs为雪层比热，J/kg·℃；M为融水，kg/s；μ为太阳辐射在雪层内的衰减系数，推荐值为40 m-1[14]。

温度控制的下边界条件

Tm=f(Tgound) orTm=const

(5)

对于该模型中的三相：

体积含量

(6)

质量含量

φi+φw+φa=1.0

(7)

各相体积含量和质量含量之间的关系

ρsφj=ρjθj(j=i,w,a)

(8)

在雪层厚度的计算上存在一个假设：通过质量守恒换算，雪层的总厚度是各相厚度的累加。即

(9)

通过热传导率λs和比热cs能体现雪层中三相综合的特点。即

λs=λiθi+λwθw+λaθa
ρscs=ρiciθi+ρwcwθw+ρacaθa
=ρs(ciφi+cwφw+caφa)

(10)

3.2 相变

3.2.1 蒸发和升华

根据潜热通量计算可蒸发和升华的雪量[15]。潜热通量先满足表层的液态水蒸发，再对表层的固态冰升华，依此逐层向下。

3.2.2 融化与冻结

通过能量平衡方程可以计算雪层的温度剖面。因为雪层的实际温度Ts(z，t)≤0 ℃，如果出现计算雪温Ts′大于0 ℃。假设融雪的临界温度Tm为0 ℃，则将雪层温度重置为0，富余能量用于升温和融化。即

Δmw=Δ(SWE×φw)=cimi(Ts′-Tm)/Lf

(11)

基于质量守恒，该雪层中的液态水含量增加，固态冰含量减少

Δmw=-Δmi

(12)

从水到冰的冻结过程反之亦然。如果雪层中θw>0，但根据能量平衡计算的雪温Ts(z，t)<0 ℃。那么，雪层液态水全部冻结且该雪层温度统一低于0 ℃，或者部分冻结且雪层呈0 ℃的冰水混合状态。

3.3 水量传递

液态水在雪层间按照下渗率传递，以满足该层的最大液态水含量为上限，剩余水量继续向下层传递。

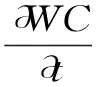
(13)

式中，WC为雪层间传递水量，kg；Kw为下渗率，kg/s；Φw_max为雪层内最大液态水质量含量

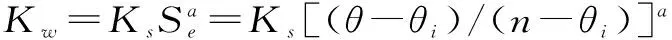
(14)

式中，θ为液态水含量；θi为毛管水含量；n为孔隙度；Se为饱和含水率(液态水含量/孔隙度)；Ks为饱和导水率，kg/s；d为雪层颗粒粒径，m；a为参数，建议值3.0[5]。

伴随融水传递过程，可能出现的情况：①雪层变薄，密度降低；②雪层全部消融；③密度低于某临界值ρmin，雪层塌陷、全融。

3.4 压实与粒径变化

(1)雪层结构

c3=c3=1 (θw=0且ρs≤150 kg/m3)

c3=e-0.046(ρs=150)(ρs>150 kg/m3)

c4=2 (θw>0)

(15)

(2)荷载雪层压力

(16)

式中，Ps为上负雪层荷载，N/m2；η为粘度系数，N·s/m2；η0=3.6×106N·s/m2。粒径变化影响雪层中液态水传输速率。本模型借鉴前人的经验公式[16]反映粒径变化过程。即

∂d/∂t=(g2/d)×0.14 (θw<0.09)
g2=4.0×10-12m2/s

(17)

4 模型应用

4.1 模型基础数据

本研究采用美国洛基山脉科罗拉多Niwot实验场(3 517 m， 40°03′N， 105°35′W)Saddle 观测点006号雪坑1996年4月25日～6月21日雪深、密度、雪温观测资料，以及Subnivean实验站相应时段内的气象观测资料，包括：降水量、入射短波辐射、反射短波辐射、大气长波辐射、地面长波辐射、气温、雪层表面感热通量、潜热通量等[17]，进行模型率定。

Niwot Ridge具有海拔高、辐射大、气温气压低、风速大的特点。Saddle观测点附近，平均每年冬季积雪深度在2 m以上[15，18]。测雪的相关项目包括初始雪深、雪温、密度剖面等，具体为：雪层底端高程、雪层顶端高程、雪层厚度、密度及雪温。

模型参数包括：时间步长Δt=1 h，空间步长(雪层厚度)Δz=1 cm；计算时段1 392 h，计算初始雪层的液态水含量为θw=0，最大液态水体积含量θw_max=6%；临界最小密度(不考虑新雪层)ρmin=300 kg/m3。

4.2 模型结果及分析

通过计算1996年4月～6月006号雪坑剖面雪层液态水含量、密度、温度变化，统计整个雪柱剖面雪深、平均密度、平均雪温与实测相应项目的对比见图1、图2和图3。

图1 计算和实测雪深对比

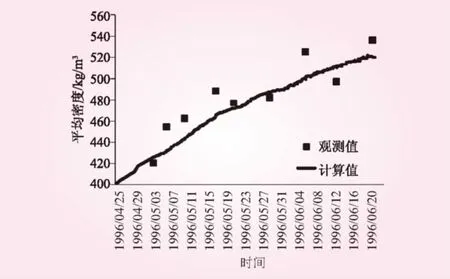
图2 计算和实测雪柱剖面平均密度对比

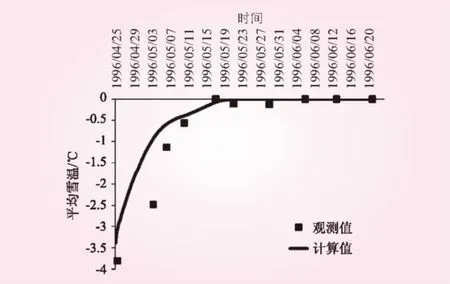
图3 计算和实测雪柱剖面平均温度对比

Snow Column模拟结果可以反映：①随着积雪消融过程的发展，雪盖密度增加、雪温升高、雪层液态水含量变大的物理过程；②模拟值基本位于实测数据的变化范围内；③相对于观测数据的波动性，模拟值更为平滑。主要原因：一是，在实际观测中风吹雪等效应会影响实测数据，具有一定随机性。本模型缺乏对风吹雪后积雪重分布的建模。二是，本模型尚未采用Fick定律和理想气体状态方程等模拟雪层中气体运移，主要通过经验公式简化考虑温度、压力影响下的压实过程，此为模型有待改进的另一个方面。

5 结 论

本文建立了基于物理过程的能量平衡融雪模型，该模型主要应用于点尺度，能详细刻画雪柱在消融过程中，密度剖面、温度剖面和液态水含量的变化过程。文中通过美国洛基山脉科罗拉多Niwot实验场006号雪坑1996年4～6月融雪观测资料，对模型进行验证。模拟结果在合理范围内，而在风吹雪模块，以及雪层中气体迁移细节处理上，仍需要进一步改进和优化。在此后的工作中，将结合006号雪坑详尽的观测资料对模型进行进一步验证和应用。

[1] 杨针娘, 刘新仁, 曾群柱, 等. 中国寒区水文[M]. 北京: 科学出版社, 2000．

[2] 秦大河, 效存德, 丁永建, 等. 国际冰冻圈研究动态和我国冰冻圈研究的现状与展望[J]. 应用气象学报, 2006, 17(6): 649- 656．

[3] 牟丽琴. 冰川积雪区流域热力学水文模型研究[D]. 北京： 清华大学, 2008．

[4] SHAMIR E, GEORGAKAKOS K P. Distributed snow accumulation and ablation modeling in the American River basin[J]. Advances in Water Resources, 2006, 29(4): 558- 570．

[5] SINGH P, SINGH V P. Snow and glacier hydrology[M]. The Netherlands: Kluwer Academic Publishers, 2001．

[6] de QUERVAIN M R. Snow structure, heat and mass flux through snow[R]. IAHS Report 107, 1: 203- 226．

[7] TODD WALTER M, BROOKS E S, McCOOL D K, et al. Process-based snowmelt modeling: does it require more input data than temperature-index modeling？[J]. Journal of Hydrology, 2005, 300(1- 4): 65- 75．

[8] LI Xingong, WILLIAMS M W. Snowmelt runoff modeling in an arid mountain watershed, Tarim Basin, China[J]. Hydrological Processes, 2008, 22(19): 3931- 3940．

[9] FONTAINE T A, CRUICKSHANK T S, ARNOLD J G, et al. Development of a snowfall-snowmelt routine for mountainous terrain for the soil water assessment tool (SWAT)[J]. Journal of Hydrology, 2002, 262(1- 4): 209- 223．

[10] AMBROISE B, FREER J, BEVEN K. Application of a generalized TOPMODEL to the small Ringelbach catchment, Vosges, France[J]. Water Resources Research, 1996, 32(7): 2147- 2159．

[11] 俞鑫颖, 刘新仁. 分布式冰雪融水雨水混合水文模型[J]. 河海大学学报： 自然科学版, 2002, 30(5): 23- 27．

[12] SINGH V P. Computer model of watershed hydrology[M]. USA: Water Resource Publications, 1995．

[13] YAN Fenglin, RAMAGE J, McKENNEY R. Modeling of high-latitude spring freshet from AMSR-E passive microwave observations[J]. Water Resources Research, 2009, 45, W11408, doi: 10.1029/2008WR007370．

[14] KONDO J, YAMAZAKI T. A prediction model for snowmelt, snow surface temperature and freezing depth using a heat balance method[J]. Journal of Applied Meteorology, 1990, 29: 375- 384．

[15] HOOD E, WILLIAMS M, CLINE D. Sublimation from seasonal snowpack at a continental mid-latitude alpine site[J]. Hydrological Processes, 1999, 13: 1781- 1797．

[16] JORDAN R E. A one-dimensional temperature model for a snow cover-Technical documentation for SNTHERM.89[C]∥Cold Regions Research & Engineering Laboratory Special Report 91-16, U.S. Army Corps of Engineers, 1991．

[17] Niwot Ridge Long Term Ecological Research (NWT LTER). http:∥culter.colorado.edu/NWT/

[18] CLINE D W. Snow surface energy exchanges and snowmelt at a continental, midlatitude Alpine site[J]. Water Resources Research, 1997, 33(4): 689-701．

AProcess-basedSnowmeltModelI:Principles

GAO Jie

(China Renewable Energy Engineering Institute, Beijing 100120, China)

A process-based energy balance snowmelt model--Snow Column is newly developed. The processes of energy conservation, phase change, mass transfer, compaction and growth of grain size are involved in the model. It could provide the changes of density profile, temperature profile and liquid water content profile varied with snowmelt processes. The observations during the period of April to June 1996 of Snowpit 006 in Niwot Ridge, Rocky Mountain Front Range of Colorado, USA are used to verify the model. The calculated results are approximately consistent with the observed. It will offer a better understanding of the response of snowpack to climate change．

snowmelt model; energy balance; Snow Column; Niwot Ridge

P339

A

0559- 9342(2017)09- 0019- 04

2017- 06- 08

中国电力建设股份有限公司项目(DJ-ZDZX-2016- 02- 01)；国家重点基础研究计划973项目(2013CB036403)

高洁(1985—)，女，安徽滁州人，高级工程师，博士，从事水文水资源、水电规划方面研究工作．

(责任编辑陈 萍)