随机交通流的组合控制预测模型和方法*
董 伟
(吉林警察学院 交通管理系,长春 130000)
控制工程
随机交通流的组合控制预测模型和方法*
董 伟
(吉林警察学院 交通管理系,长春 130000)
为了解决交通流预测中的时变性、随机性和不确定性等问题,提出了一种新的组合控制预测算法.该方法利用多尺度的小波分析方法将交通流量分解为均匀部分和随机部分,并根据状态的动态变化构建了组合控制预测模型,分别利用支持向量机回归和Markov链法来预测交通流的均匀序列和随机序列,同时基于准动态规划方法来计算最优控制向量和相应的控制矩阵,从而动态选择训练数据得到最优预测结果,并采用实际数据进行实验验证与比较.结果表明,本文方法得到的平均相对误差和均方差比其他方法低74%和85%,得到的均等系数高6%,从而验证了本文方法的可行性和有效性.
交通流预测;多尺度小波;支持向量机回归;马尔科夫链;准动态规划;最优控制向量;最优控制矩阵;组合控制预测
随着我国城市化进程的不断加快,交通流量日益增大,交通堵塞问题越来越严重,这已经影响到居民的正常生活,成为制约经济和社会发展的一个主要因素.在这种背景下,利用现代高新科技手段而发展起来的智能交通控制系统能够较好地改善城市交通状况和提高交通运行能力,已经成为现代交通控制领域的研究热点[1-2].
交通流是指被测路段上单位时间内的车流量总和,交通流量的变化是随机的、时变的和非线性的,对城市交通流量进行预测以获取准确的交通信息来实现交通控制、管理和诱导,是智能交通控制系统发展的前提和关键,国内外许多专家和学者都围绕该内容开展了大量的研究.陆琳等[3]人为了解决交通流实时变化和高度非线性的问题,提出了基于灰色系统和神经网络的组合模型;卢建中等[4]人为了提高BP神经网络预测模型在交通流预测中的准确性,使用改进的遗传算法来优化权值和阈值的选取;满瑞君等[5]人提出了多尺度小波支持向量机的交通流预测模型,能够得到比神经网络更好的预测效果;常刚等[6]人在预测短时交通流时,利用区域路网的时空依赖性来改进时空自回归差分移动平均模型的空间权重矩阵;傅贵等[7]人利用核函数将短时交通流问题转化为线性回归问题,再使用支持向量机回归来求解.
然而,交通系统是一个复杂的非线性系统,它受诸多因素影响,具有时变性、随机性和不确定性等特点.一些传统的预测方法往往存在计算量大、精度低、鲁棒性差、依赖历史数据量多和预测时间间隔较长等缺陷,较难得到准确的预测结果.针对上述问题,本文依据交叉口交通流动态变化的特性,基于多尺度分析和准动态规划的思想构建了交通流的组合控制预测模型,采用支持向量机回归和Markov链得到其均匀分量和随机分量,同时利用准动态规划方法计算最优控制向量,从而得到最优预测结果,最后用实测数据来验证本文方法的有效性和可行性.
1 交通流的组合控制预测模型
1.1 交通流建模
影响交叉口路段交通流的因素主要有路段的交通构成、交叉口的渠化和信号控制等,由于交通流始终处于不断变化的状态,因此采用Webster模型[8]来计算交通流中的延误,其表达式为
d=du+dr-0.65(C/q2)1/3x2+5λ
(1)
式中:d为位于交叉口处的平均车辆延误;C为控制信号的周期;q为交通量;x为饱和度;λ为绿信比;du和dr分别为交通流的均匀延误和随机延误,主要由车辆运行的周期性和随机性引起,其表达式分别为

(2)
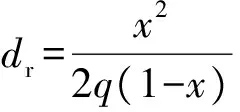
(3)
由式(1)~(3)可以看出,在信号控制的周期内,交通序列呈现出均匀特性和随机特性.根据Webster周期计算公式,最佳周期为
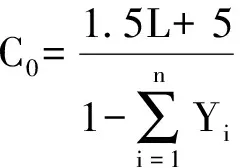
(4)
式中:L为损失时间;Yi=qi/Sq为第i相位交通流量qi与饱和流量Sq的比值;n为相位数.由于L取值固定,所以C0的值取决于交通流量的和.据此,选取某个控制信号周期内的交通流量之和作为观测量,其表达式为

(5)
式中,U(t)和R(t)分别为交通流的均匀序列和随机序列.
1.2 交通流小波分析
为了能够较准确地预测交通流,需要理清其中的均匀序列和随机序列.假设交通流中的随机部分服从广义平稳随机过程,且满足高斯分布,那么利用多尺度小波分析来分离出高频和低频信号,从而分解出其中的均匀部分和随机部分,再对不同的部分采用不同的方法进行预测.
对于平方可积的连续信号f(x),其小波变换为
(6)
式中,ψ(a,b)(x)为小波函数,参数a和b分别为伸缩因子和平移因子.
利用Mallat小波对交通流序列进行M个尺度的小波分解,可得
q(t)=U1(t)+R1(t)=U2(t)+R2(t)+R1(t)=
(7)
式中,UM(t)和Riq(t)分别为交通流中的低频量和高频量.
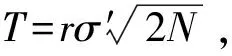
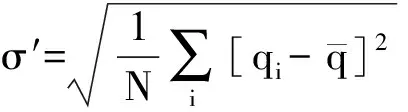
(8)
由多尺度小波分解得到的低频量和量化之后的高频量进行小波重构,可以得到交通流序列信号的均匀量U(t)和随机量R(t).
1.3 预测模型
考虑到相关联交叉口的交通流量对交叉口的预测结果存在影响,其预测信息的表达式为
q(t+1)=φ[q(t),…,q(t-n+1),…,
φb(t),φc(t),φd(t)]
(9)
式中:φ(·)为预测模型方法;q(t)为交叉口在时刻t的实际交通流量;φb(t),φc(t),φd(t)分别为与当前交叉口相关联的b、c、d交叉口在前t个时刻的交通流量.如果取所有时刻相关联交叉口的交通流量进行训练会导致计算量较大,而且当训练数据的时刻与预测数据的时刻相隔太远时,预测精度较低.因此,本文使用特定时刻特定交叉口的交通流量作为预测模型的输入向量p(t),即
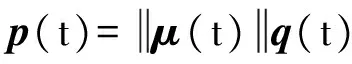
(10)
q(t)=[qa(t),qa(t-1),qb(t),
qb(t-1),qc(t),qc(t-1)]
(11)
由控制向量μ(t)=[1,1,0,1,1,0]得到控制矩阵,即
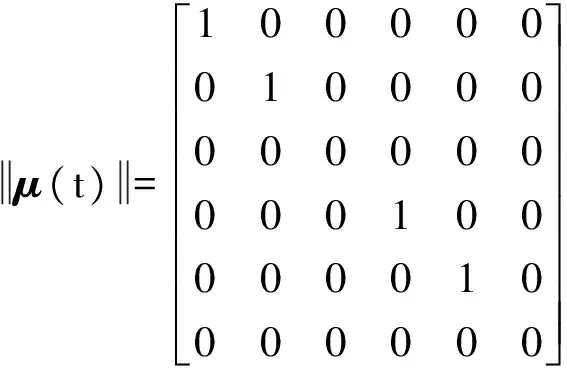
(12)
将其代入式(10)可得
q(t)=[qa(t),qa(t-1),0,
qb(t-1),qc(t),0]
(13)
式(13)即为选择a交叉口t时刻和t-1时刻、b交叉口t-1时刻、c交叉口t时刻的交通流数据作为组合控制预测模型的输入.
该组合控制预测模型包含了控制模型和组合预测模型,如图1所示.控制模型的控制量由过去时刻的数据、相关联的数据和反馈参数组成,预测模型采用的训练数据为特定时刻和特定交叉口的交通流量,利用组合预测模型结合控制量得到的优化预测结果再对控制模型进行改进.
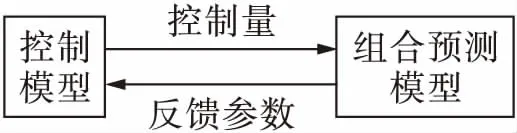
图1 组合控制预测模型框图Fig.1 Block diagram of combined control predictive model
2 交通流的组合控制预测方法
2.1 均匀部分的SVMR预测
交通流的均匀序列具有较强的非线性,利用SVM可以较好地解决该问题,而SVMR是SVM在回归估计中的扩展,可以使得所有样本逼近超平面,从而得到总偏差最小的结果.
SVMR待解决的问题为
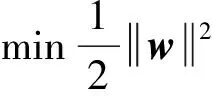
(14)
该问题也可以转换为一个二次规划问题,在求解过程中,核函数的选择是关键.取xi和yi分别为稳态交通流序列的自变量和预测值,为了寻找两者之间的数学关系yi=f(xi),采用ε-SVM回归方法[10],具体的预测步骤如下:
1) 选取训练样本,并进行去噪和归一化处理.假设之前时刻和当前时刻的交通流为qi(t-n),qi(t-n-1),…,qi(t),则下一时刻的训练样本集为
xi=[qi(t-n),qi(t-n-1),…,qi(t)]
(15)
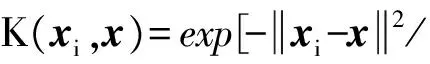
3) 建立目标函数,通过求解式(9)来寻找最优的分类面.
4) 构建决策函数,即

(16)
各变量含义见文献[10],通过式(16)即可计算出稳态交通流序列未来时刻的预测值.
2.2 随机部分的Markov链预测
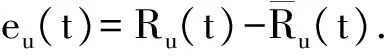
m>2D/(0.674 5S0)
(17)
Eu∈[(u-1)D/(m-1),uD/(m-1)]
(u=1,2,…,m)
(18)
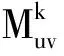

(19)
将每种状态转移到其他状态的转移概率进行合成,可得到状态转移概率矩阵,即

2.3 基于准动态规划的交通流组合控制预测
准动态规划包含三个部分:评价部分、模型部分和执行部分.准动态规划的组合控制预测过程如下:
2) 计算执行部分的流量误差,即
(20)
式中,ΔT、q(t)和qp(t)分别为预测时间间隔、t时刻的实际流量和预测流量.
3) 将[x(t),μ(t)]T作为评价部分的输入得到输出J*(t),令t=t+1得到J*(t+1).
4) 最小化Q(t)得到评价部分的权值,即
(21)
5) 最小化U(t)+γJ*(t+1)得到执行部分的取值,其中,γ为权重参数.
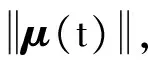
3 实验结果与分析
选取某路口自动检测系统采集的交通流量数据进行实验验证,该数据的采集持续时间为连续三日的上午七时至晚上七时,采集的时间间隔为5min,一共记录了435个数据.
为了能够体现本文算法的优越性,将本文算法与文献[5]和文献[11]方法进行比较,并选用三个评价指标,分别为平均相对误差RME、均方差MSE和均等系数EC,其表达式分别为

(22)
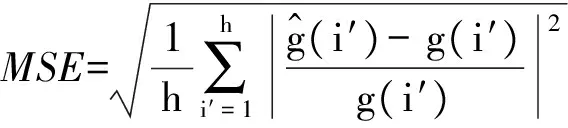
(23)
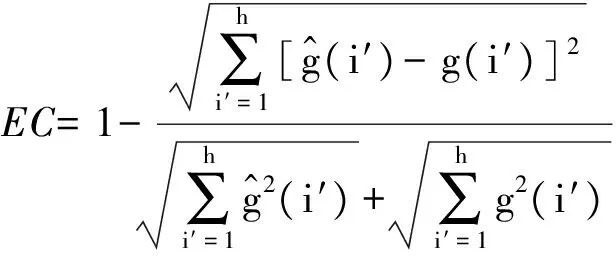
(24)
将交通流数据分为两部分,每日的前60个数据作为训练集,用来构造预测模型;每日的后85个数据作为测试集,用来检测算法的预测准确度.图2~4分别为采用三种不同方法对连续三天的交通流量进行预测的结果比较,图5~7分别为三种方法得到的预测值与实际值偏差的绝对值结果比较,表1~3为三种性能评价指标在不同时间的结果比较.由表1~3可以看出,本文方法得到的平均相对误差和均方差比文献[5]和文献[11]的方法低74%和85%,得到的均等系数高6%.对比图和表中的结果可以得出以下结论:文献[5]的方法所对应的预测结果误差度最高、拟合度最低,表明本文提出的组合预测方法在预测准确度上明显优于基于单一预测模型的方法;与文献[11]的方法相比,本文方法对应的误差度要低、拟合度要高,因此,本文提出的组合预测方法优于文献[11]的组合预测方法,能够更好地解决随机交通流的时变性、随机性和不确定性等问题,从而可以更好地动态修正随机交通流的预测值.综上可知,本文方法具有预测准确度较高和动态适应性强等优点.
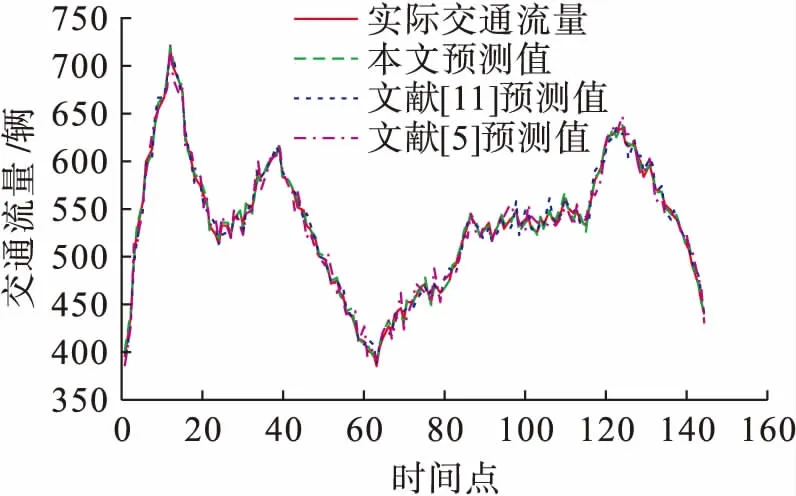
图2 三种方法预测结果对比(第一日)Fig.2 Comparison in forecasted results for three methods (first day)
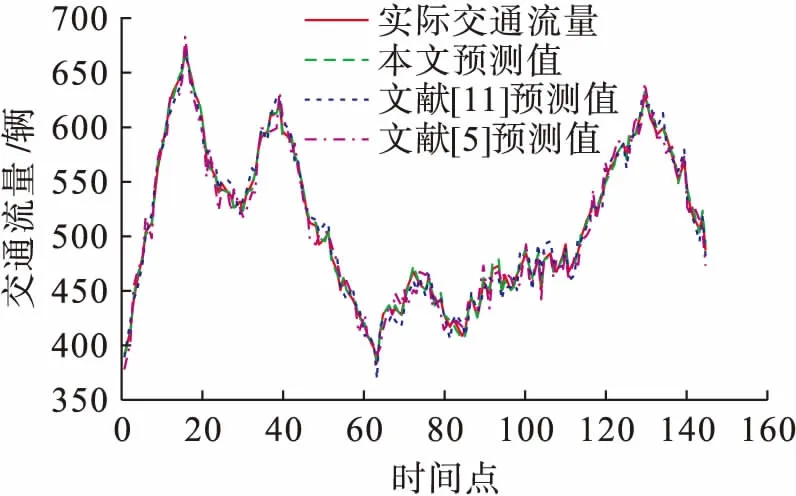
图3 三种方法预测结果对比(第二日)Fig.3 Comparison in forecasted results for three methods (second day)
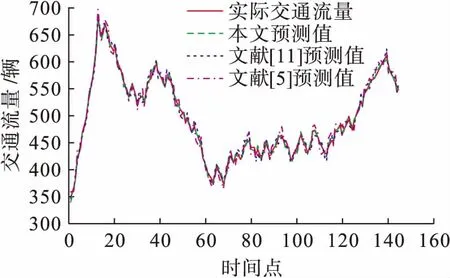
图4 三种方法预测结果对比(第三日)Fig.4 Comparison in forecasted results for three methods (third day)
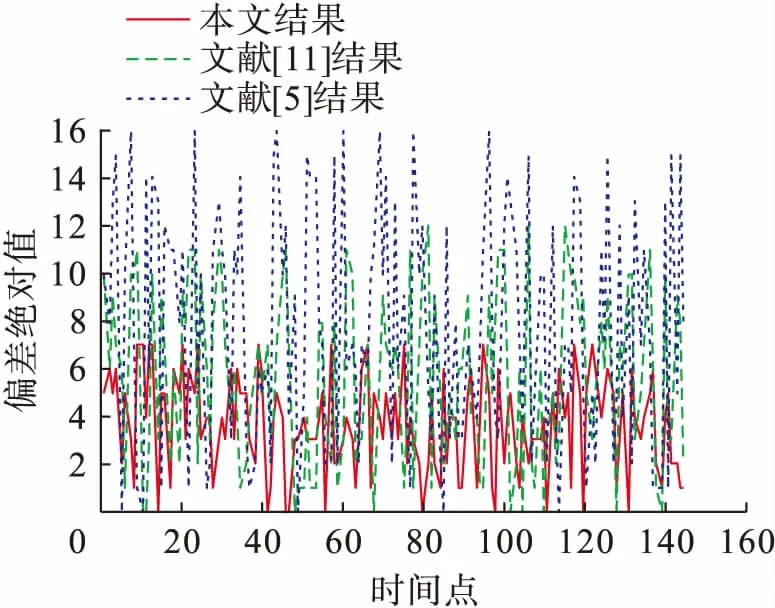
图5 三种方法偏差绝对值对比(第一日)Fig.5 Comparison in absolute errors for three methods (first day)

图6 三种方法偏差绝对值对比(第二日)Fig.6 Comparison in absolute errors for three methods (second day)
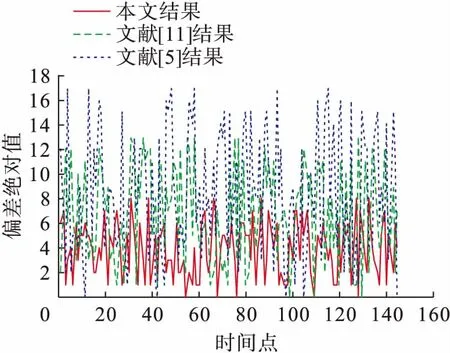
图7 三种方法偏差绝对值对比(第三日)Fig.7 Comparison in absolute errors for three methods (third day)
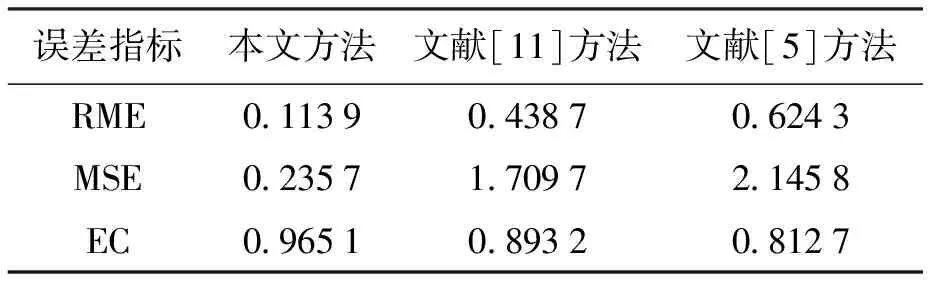
表1 三种方法性能指标评价结果(第一日)Tab.1 Evaluation results of performance indexes for three methods (first day)
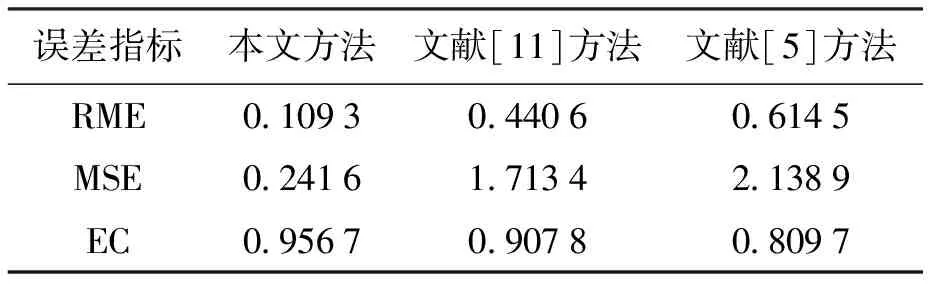
表2 三种方法性能指标评价结果(第二日)Tab.2 Evaluation results of performance indexes for three methods (second day)
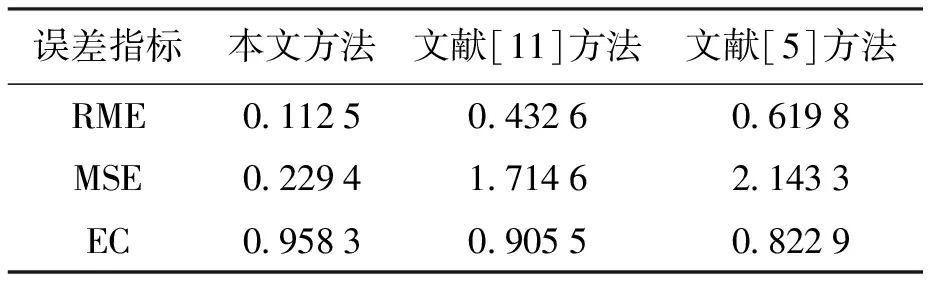
表3 三种方法性能指标评价结果(第三日)Tab.3 Evaluation results of performance indexes for three methods (third day)
4 结 论
针对随机交通流预测中的时变性和不确定性等问题,本文通过对交通流的多尺度小波进行分析,将其分解为均匀序列和随机序列,并基于状态的动态变化特性构建组合控制预测模型,在此基础上提出了基于支持向量机回归和Markov链的组合预测方法.利用准动态规划思想动态选择训练数据得到最优预测结果,采用实测数据对该方法进行实验验证,并与其他方法做了比较分析.实验结果表明,本文方法对应的平均相对误差和均方差比文献[5]和文献[11]方法低74%和85%,对应的均等系数则高6%.因此,该方法能够显著提高随机交通流量的预测准确度,较好地解决了交通流量实时预测中存在的时变性、随机性和不确定性等问题,预测性能明显优于单一预测方法和传统的组合预测方法,具有较好的应用价值.
[1] 高慧,赵建玉,贾磊.短时交通流预测方法综述 [J].济南大学学报(自然科学版),2008,22(1):88-94.
(GAO Hui,ZHAO Jian-yu,JIA Lei.Summary of short-time traffic flow forecasting methods [J].Journal of University of Jinan (Science and Technology),2008,22(1):88-94.)
[2] 袁健,范炳全.交通流短时预测研究进展 [J].城市交通,2012,10(6):73-79.
(YUAN Jian,FAN Bing-quan.Synthesis of short-term traffic flow forecasting research progress [J].Urban Transport of China,2012,10(6):73-79.)
[3] 陆琳,张虹.城市短时交通流预测仿真研究 [J].计算机仿真,2012,29(5):326-328.
(LU Lin,ZHANG Hong.Simulation of city short-time traffic flow forecasting [J].Computer Simulation,2012,29(5):326-328.)
[4] 卢建中,程浩.改进GA优化BP神经网络的短时交通流预测 [J].合肥工业大学学报(自然科学版),2015,38(1):127-131.
(LU Jian-zhong,CHENG Hao.Short-term traffic flow forecast based on modified GA optimized BP neural network [J].Journal of Hefei University of Technology (Science and Technology),2015,38(1):127-131.)
[5] 满瑞君,梁雪春.基于多尺度小波支持向量机的交通流预测 [J].计算机仿真,2013,30(11):156-159.
(MAN Rui-jun,LIANG Xue-chun.Traffic flow forecasting based on multiscale wavelet support vector machine [J].Computer Simulation,2013,30(11):156-159.)
[6] 常刚,张毅,姚丹亚.基于时空依赖性的区域路网短时交通流预测模型 [J].清华大学学报(自然科学版),2013,53(2):215-221.
(CHANG Gang,ZHANG Yi,YAO Dan-ya.Short-term traffic flow forecasting model for regional road network based on spatial-temporal dependency [J].Journal of Tsinghua University (Science and Techno-logy),2013,53(2):215-221.)
[7] 傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型 [J].华南理工大学学报(自然科学版),2013,41(9):71-76.
(FU Gui,HAN Guo-qiang,LU Feng,et al.Short-term traffic flow forecasting model based on support machine regression [J].Journal of South China University of Technology (Natural Science Edition),2013,41(9):71-76.)
[8] Han L D,Li J M,Urbanik T.Impacts of intercycle demand fluctuations on delay [J].Journal of Transportation Engineering,2009,135(5):288-296.
[9] 张敬磊,王晓原.基于非线性组合模型的交通流预测方法 [J].计算机工程,2010,36(5):202-204.
(ZHANG Jing-lei,WANG Xiao-yuan.Traffic flow prediction method based on non-linear hybrid model [J].Computer Engineering,2010,36(5):202-204.)
[10]Vapnik V.统计学习理论 [M].北京:电子工业出版社,2015.
(Vapnik V.Statistical learning theory [M].Beijing:Publishing House of Electronics Industry,2015.)
[11]杜长海,黄席樾,杨祖元,等.基于神经网络和Markov链的交通流实时滚动预测 [J].系统仿真学报,2008,20(9):2464-2468.
(DU Chang-hai,HUANG Xi-yue,YANG Zu-yuan,et al.Real-time rolling traffic flow forecasting based on neural networks and Markov chains [J].Journal of System Simulation,2008,20(9):2464-2468.)
Combinedcontrolpredictivemodelandmethodforstochastictrafficflow
DONG Wei
(Department of Traffic Management, Jilin Police College, Changchun 130000, China)
In order to solve the problem of time variability, randomness and uncertainty in the traffic flow forecasting, a new combined control predictive algorithm was proposed.The proposed method divided the traffic flow into uniform part and random part with the multi-scale wavelet analysis method.The combined control predictive model was established according to the dynamic change of states.The uniform and random sequences of traffic flow were predicted with the support vector machine regression and Markov chain method, respectively.Based on the quasi dynamic programming method, the optimal control vector and the corresponding control matrix were calculated.Hence, the optimal prediction results could be obtained through the dynamic selection of training data.Furthermore, the experimental verification and comparison were implemented with the actual data.The results show that the average relative error and mean square deviation obtained with the proposed method are 74% and 85% lower than those of other methods, and the obtained equality coefficient is 6% higher than that of other methods.Therefore, the feasibility and effectiveness of the proposed method can be verified.
traffic flow forecasting; multi-scale wavelet; support vector machine regression; Markov chain; quasi dynamic programming; optimal control vector; optimal control matrix; combined control prediction
2017-05-16.
国家自然科学基金资助项目(61403160).
董 伟(1972-),男,吉林长春人,副教授,硕士,主要从事道路交通管理等方面的研究.
* 本文已于2017-12-21 14∶22在中国知网优先数字出版.网络出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171221.0848.002.html
10.7688/j.issn.1000-1646.2018.01.16
TP 391
A
1000-1646(2018)01-0088-06
钟 媛 英文审校:尹淑英)

