永磁同步电机伺服系统自适应迭代学习控制*
朱国昕,雷鸣凯,赵希梅
(1.沈阳工业大学 电气工程学院,沈阳 110870;2.沈阳军区总医院 医学工程科,沈阳 110016)
永磁同步电机伺服系统自适应迭代学习控制*
朱国昕1,2,雷鸣凯1,赵希梅1
(1.沈阳工业大学 电气工程学院,沈阳 110870;2.沈阳军区总医院 医学工程科,沈阳 110016)
针对执行重复性任务的永磁同步电机伺服系统,由于参数摄动、随机扰动等不确定因素影响导致的跟踪精度下降,误差发散问题,提出一种自适应迭代学习控制方法.该方法在PD型反馈控制的基础上增加自适应迭代项对控制律中未知参数进行迭代学习,减少不确定因素对系统性能的影响.建立了含有不确定性扰动的系统模型和PMSM自适应迭代学习控制系统,并且基于Lyapunov稳定性理论,分析了该方案的收敛性.结果表明,与传统PD型ILC相比,该方法收敛速度更快,跟踪精度更高,可有效改善系统的性能.
永磁同步电机;迭代学习控制;自适应迭代学习控制;反馈控制;参数摄动;跟踪误差;收敛速度;伺服系统
永磁同步电机(PMSM)以其体积小、结构简单、转动惯量低及功率密度高等优点在工业机器人、高精度数控机床等伺服控制领域有着广泛的应用.但是由于其易受参数摄动、摩擦扰动等非线性因素的影响,以及传统PID控制器性能的限制,难以获得理想的位置跟踪效果[1-2],因此,消除这些非线性因素的影响,寻找更好的控制方法对提升PMSM伺服系统的性能至关重要.
将先进的控制理论用于PMSM伺服系统,通过提高系统的动态性能来提高跟踪精度是一种常见的方法.文献[3]采用预测函数对系统进行控制,使其跟踪性能有较大提高,并且具有一定的抗扰能力,但控制精度较低;文献[4]提出一种模糊预测控制对参数进行改善,但是算法较为复杂,难以实际应用;文献[5]采用滑模变结构控制,通过对系统滑模面的设计,较好地实现了系统的精确定位,但是电机的抖振现象难以避免;文献[6]采用扰动观测器对有限带宽内的扰动进行补偿,但是要求系统有精确的模型.
迭代学习控制(ILC)适用于执行重复任务的伺服控制系统,其根据前次运行的系统信息来校正当前控制量,可以有效提高控制精度.该方法无需知道被控对象的具体数学模型,控制器设计简单,在实际工程领域中得到了广泛应用[7-9].然而实际系统中通常存在不确定性扰动[10](如参数摄动、不可测量的随机扰动等),而自适应控制基于Lyapunov稳定性理论,可设计参数自适应律,对含有参数不确定性的复杂非线性系统可实现系统的镇定和对目标轨迹的渐近跟踪[11].本文提出一种自适应迭代学习控制(AILC)方法,自适应项通过执行重复任务进行迭代学习,辨识出控制律中未知参数,获得前馈控制量来补偿系统不确定性.同时加入反馈控制器来增强系统的鲁棒性及稳定性,滤波器使系统能够抑制高频干扰,并通过系统实验证明了该方案的有效性.
1 PMSM数学模型
为方便分析,忽略铁芯饱和及涡流与磁滞等损耗,并假设相绕组感应电动势为正弦波.经过矢量控制坐标变换实现电机解耦,PMSM的数学模型可表示为
(1)
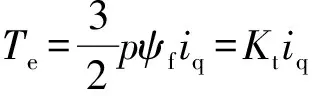
(2)
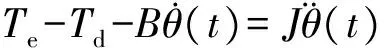
(3)
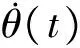
扰动主要包括非线性摩擦扰动及齿槽转矩波动等,非线性摩擦模型选用Stribeck模型,表示为
(4)
式中:Tc为库仑摩擦转矩;Tm为最大静摩擦转矩;a为一个非常小的转数,其与摩擦、转速关系曲线如图1所示.

图1 摩擦转速关系曲线Fig.1 Friction-rotated speed relationship curves
齿槽转矩模型可表示为
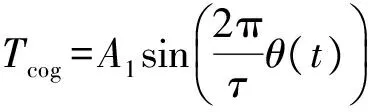
(5)
式中:A1为齿槽转矩幅值;τ为极距.由式(2)~(5)可推出PMSM的动态方程为
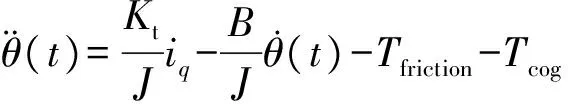
(6)
然而实际系统中由于温度变化、设备老化等不可控因素,模型存在参数摄动,会引起系统不确定性,因此需考虑参数摄动问题,可将式(6)改写为
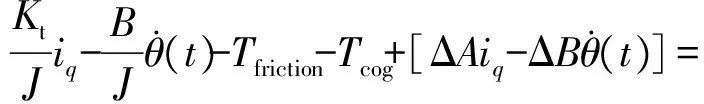
(7)
式中:ΔA、ΔB为系统参数摄动所引起的不确定量;D为系统不确定量的总和.设D为有界不确定量D=Hrand(1)sint,其中,H为不确定量扰动的幅值.
2 PMSM控制系统设计
2.1 PMSM自适应迭代学习控制系统
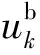
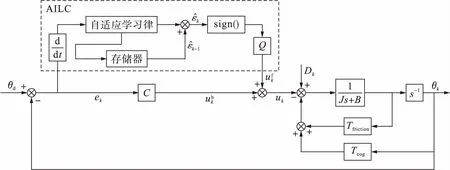
图2 PMSM自适应迭代学习控制系统框图Fig.2 Block diagram of AILC system for PMSM
2.2 控制器设计
由图2可得

(8)
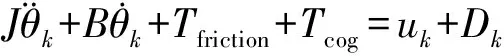
(9)
假定电机转子位置和速度可以通过反馈获得,则需设计控制律,使θk在任意时间t均有界,并且k→∞时,θk收敛于对应期望轨迹θd.
根据以上描述做出如下假设:
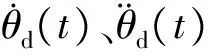
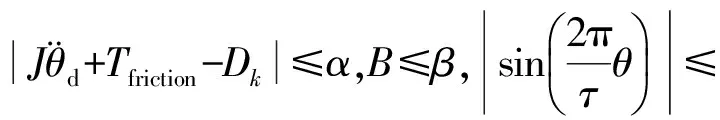
由以上假设可以看出,系统的初始状态相同且参数有界,其与机械手臂运动状态相吻合,因此,该系统适用于机械手臂系统.考虑其特性及以上假设,设计控制律和参数自适应迭代学习律分别为
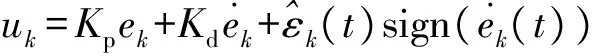
(10)
(11)
2.3 收敛性分析
取Lyapunov函数为
(12)
(13)
则
ΔWk=Wk-Wk-1=
(14)
(15)
根据式(9)可得
(16)
由假设3)可得
γ)sign(ek)-uk+Kpek]dt=
(17)
将式(10)、(11)及式(17)代入式(14),可得
(18)
以上推导说明Wk为非增序列,接下来证明W0的有界性.
对W0求导可得
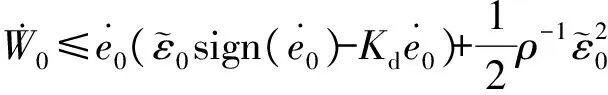
(19)
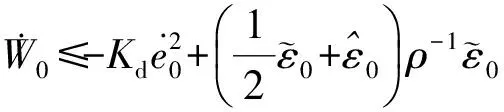
(20)
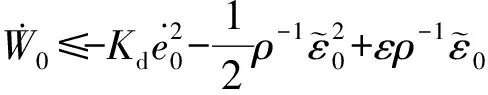
(21)
根据杨氏不等式,对于任何λ>0,不等式

(22)
恒成立,可推出
(23)
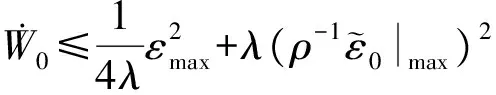
(24)
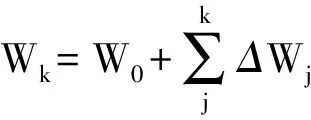
(25)
由式(18)可得
(26)
进而可推出
(27)
3 系统实验分析
为了验证所提出方案的有效性,对PMSM伺服控制系统进行实验验证.假设不确定量扰动为D=0.5rand(1)sint,PMSM参数为:额定电压200 V,额定转速5 000 r/min,额定转矩10 N·m,定子电阻2.875 Ω,d轴电感0.85 mH,q轴电感0.85 mH,永磁体磁链0.175 Wb,粘滞摩擦系数0.01 N·m·s,转动惯量8×10-2kg·m2,极对数4,实验中给定的期望位置信号为y=4sin(2πt).利用均方根误差作为跟踪性能的指标,其表达式为
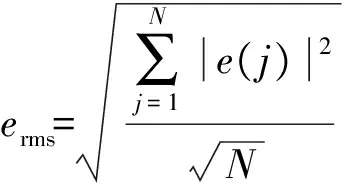
(28)
选择PD反馈控制器参数为Kp=5,Kd=8,自适应学习增益为ρ=30,滤波器Q中1/ω值取为0.02,迭代次数为20次,对电机进行位置跟踪控制曲线如图3所示.由图3可以看出,经过20次迭代,实际位置与期望轨迹基本重合,其跟踪效果良好.
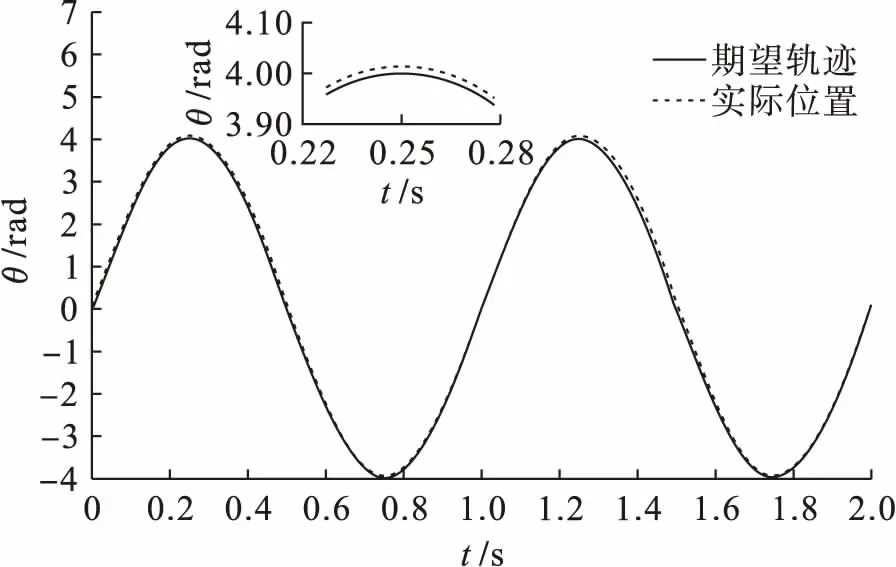
图3 位置跟踪过程曲线Fig.3 Location tracking process curve
图4为自适应迭代项在第20次迭代时的变化情况.由图4可以看出,除了初始阶段,自适应项基本符合周期为0.5 s的变化,而且其值始终为正,符合自适应学习律.
图5、6分别为PD型ILC和AILC迭代20次后的跟踪误差曲线.由图5可以看出PD型ILC的最大跟踪误差约为5.1×10-3rad;而图6中AILC的最大跟踪误差仅为1.7×10-3rad,由此可以看出AILC的最大位置跟踪误差减小了约2/3.
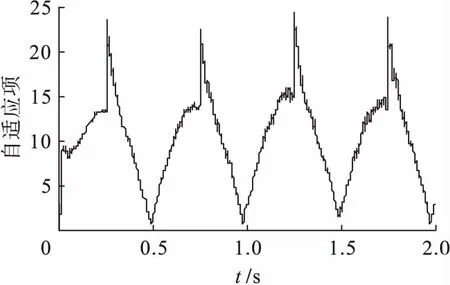
图4 自适应项变化曲线Fig.4 Adaptive item change curve
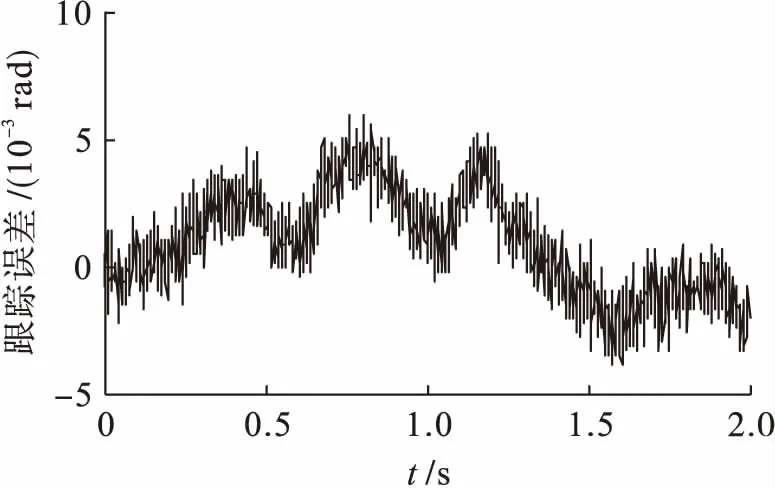
图5 PD型ILC位置跟踪曲线Fig.5 PD type ILC location tracking curve

图6 AILC位置跟踪曲线Fig.6 AILC location tracking curve
图7为PD型ILC和AILC迭代的均方根误差曲线.由图7可以看出,采用AILC时系统的收敛速度更快,而且跟踪精度更高,均方根误差基本较为稳定;而采用PD型ILC时,均方根误差值从第13次迭代时开始有上升发散趋势,并且变得不稳定.这是因为参数摄动所引起的不确定性扰动为随机的非重复性扰动,而PD型ILC由于对其只能积累,不能抑制,因此均方根误差会随着迭代次数的增大而变得不稳定甚至发散.
图8为不确定扰动幅值变化后两种方法的位置均方根误差曲线,在第10次迭代时设扰动幅值改变为D=1.5rand(1)sint.由图8可以看出AILC均方根误差可以较快恢复平稳,而PD型ILC在短暂下降后又继续上升,误差发散.由此也可以看出在扰动幅值突变的情况下,AILC也可以有效工作.
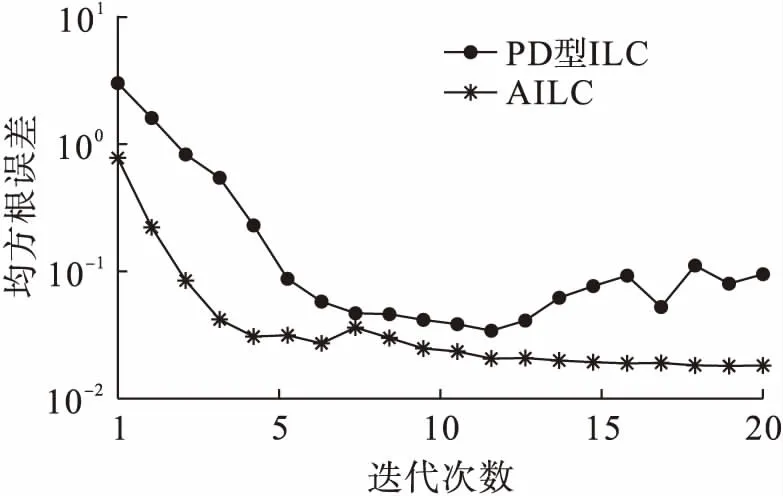
图7 随迭代次数变化的位置均方根误差Fig.7 Root mean square error of location with change of iteration times
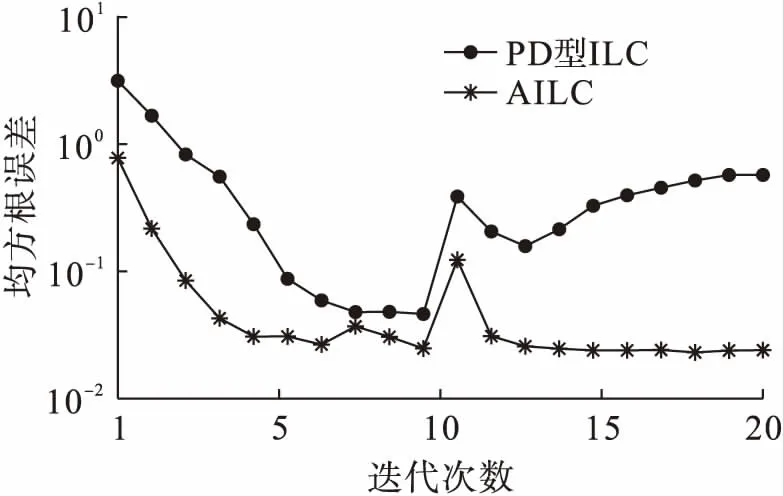
图8 不确定扰动幅值变化后的位置均方根误差Fig.8 Root mean square error of location with change of uncertain disturbance amplitude
4 结 论
针对PMSM伺服系统运行过程中存在的由参数摄动所引起的不确定性问题,提出了一种AILC方案.由于参数摄动所引起的不确定性为随机扰动,具有非重复性,传统ILC难以有效解决.而本文利用自适应迭代项辨识控制律参数,实时调整控制量补偿不确定性,同时利用PD反馈控制保证系统的鲁棒性,可有效减弱这种不确定性对系统的不利影响.该方案较为简单,调节参数较少且不需要较大存储空间,适合于实际应用.实验结果也表明,所设计的AILC方案具有良好的效果.
[1] 王伟华,肖曦.永磁同步电机高动态响应电流控制方法研究 [J].中国电机工程学报,2013,33(21):117-123.
(WANG Wei-hua,XIAO Xi.A current control method for permanent magnet synchronous motors with high dynamic performance [J].Proceedings of the CSEE,2013,33(21):117-123.)
[2] Chen M Y,Lu J S.High-precision motion control for a linear permanent magnet lron core synchronous motor drive in position platform [J].IEEE Transactions on Industrial Informatics,2014,10(1):99-108.
[3] 夏泽中,张光明.预测函数控制及其在伺服系统中的仿真研究 [J].中国电机工程学报,2005,25(14):130-134.
(XIA Ze-zhong,ZHANG Guang-ming.Design and evaluation of predictive functional control for a servo system [J].Proceedings of the CSEE,2005,25(14):130-134.)
[4] Zhang L B,Wu T,Huang F L.A coupling motional control method based on parametric predictive and variable universe fuzzy control for multi-axis CNC machine tools [J].The International Journal of Advanced Manufacturing Technology,2014(74):1094-1114.
[5] 方斯琛,周波.滑模控制的永磁同步电机伺服系统一体化设计 [J].中国电机工程学报,2009,29(3):96-101.
(FANG Si-chen,ZHOU Bo.Integrated design for permanent magnet synchronous motor servo systems based on sliding mode control [J].Proceedings of the CSEE,2009,29(3):96-101.)
[6] Mohamed A R I.Design and implementation of a robust current control scheme for a PMSM vector drive with a simple adaptive disturbance observer [J].IEEE Transactions on Industrial Electronics,2007,54(4):1981-1988.
[7] 张杰.重复/迭代学习控制器的设计与实现 [D].杭州:浙江工业大学,2012:15-16.
(ZHANG Jie.Design and implementation of repetitive controller and iterative learning controller [D].Hangzhou:Zhejiang University of Technology,2012:15-16.)
[8] 赵希梅,马志军,朱国昕.永磁直线同步电机自适应PD型迭代学习控制 [J].沈阳工业大学学报,2016,38(1):7-12.
(ZHAO Xi-mei,MA Zhi-jun,ZHU Guo-xin.Adaptive PD type iterative learning control for permanent magnet linear synchronous motor [J].Journal of Shenyang University of Technology,2016,38(1):7-12.)
[9] 王丽梅,郭宜兴.基于迭代学习控制的混合误差轮廓控制 [J].沈阳工业大学学报,2014,36(6):601-606.
(WANG Li-mei,GUO Yi-xing.Hybrid error contour control based on iterative learning control [J].Journal of Shenyang University of Technology,2014,36(6):601-606.)
[10]Lee K W,Park S,Jeong S.A semless transition control of sensorless PMSM compressor drives for improving efficiency based on a dual-mode operation [J].IEEE Transactions on Power Electronics,2015,30(3):1446-1456.
[11]宋君君,于少娟,彭昌.基于AMEsim的自适应控制在电液力伺服系统研究 [J].工业控制计算机,2012,25(6):34-36.
(SONG Jun-jun,YU Shao-juan,PENG Chang.Simulation of electric hydraulic servo system controlled adaptive based on AMEsim [J].Industrial Control Compute,2012,25(6):34-36.)
Adaptiveiterativelearningcontrolforpermanentmagnetsynchronousmotorservosystem
ZHU Guo-xin1, 2, LEI Ming-kai1, ZHAO Xi-mei1
(1.School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China; 2.Medical Engineering Department, The General Hospital of Shenyang Military, Shenyang 110016, China)
Aiming at the problem that the tracking accuracy reduces and the error is divergent due to such uncertain factors as parameter perturbation and stochastic disturbance in the process of performing repetitive tasks for permanent magnet synchronous motor (PMSM) servo system, an adaptive iterative learning control (AILC) method was proposed.Based on the PD feedback control, an adaptive iterative term was added to perform the iterative learning of unknown parameters in the control law to reduce the effect of uncertain factors on the system performance.Both system model with the uncertain disturbance and PMSM adaptive iterative learning control system were established, and the convergence of the scheme was analyzed based on Lyapunov stability theory.The results demonstrate that compared with conventional PD type ILC, the proposed method has faster convergence rate and higher tracking accuracy, and can effectively improve the system performance.
permanent magnet synchronous motor (PMSM); iterative learning control (ILC); adaptive iterative learning control (AILC); feedback control; parameter perturbation; tracking error; convergence rate; servo system
2016-09-26.
辽宁省教育厅科学技术研究项目(L2013060);沈阳市科技计划资助项目(F12-277-1-70).
朱国昕(1966-),男,辽宁沈阳人,高级工程师,博士,主要从事直线伺服、数控技术及鲁棒控制等方面的研究.
* 本文已于2017-10-25 21∶13在中国知网优先数字出版.网络出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171025.2113.050.html
10.7688/j.issn.1000-1646.2018.01.02
TM 351
A
1000-1646(2018)01-0006-06
景 勇 英文审校:尹淑英)

