光伏出力的模糊区间预测

陈云龙，殷 豪，黄 强，周亚武

（广东工业大学自动化学院，广东 广州 510006）

新能源发电技术

光伏出力的模糊区间预测

陈云龙，殷 豪，黄 强，周亚武

（广东工业大学自动化学院，广东 广州 510006）

针对光伏输出功率的点预测精度不足、传统支持向量机（SVM）在参数优化方面存在的固有缺陷等问题，根据模糊信息粒化理论和纵横交叉算法，提出一种基于CSO-SVM和模糊信息粒化理论的光伏出力模糊区间预测方案。结果表明：该方案可以得到较好的点预测值及其置信区间，某种程度上解决了传统点预测结果的信息局限性。

区间预测；支持向量机（SVM）；模糊信息粒化；置信区间

作为清洁的可再生能源，太阳能越来越受到人们重视，光伏发电是利用太阳能的方式之一［1］，而光伏发电系统功率输出与环境因素变化较密切［2］，气象条件的不确定性使得光伏功率输出具有很大的随机性和波动性［3-4］，因此，大规模光伏并网时，电力系统的安全运行和电能质量将受极大影响［5］。由此可见，光伏预测技术对电网的稳定运行具有重大意义［6］。

1 研究现状及需要解决的问题

1.1 研究现状

人们对光伏功率预测研究主要是集中在确定性的点预测［7-8］上，所谓点预测即是根据历史光伏数据和某些环境数据，利用统计学原理，建立数学模型，从而预测出未来的光伏出力。近些年，建立在结构风险最小化原则以及VC维（Vapnik-Chervonenkis Dimension）基础上的支持向量机法（support vector machine,SVM）［9-10］越来越受人们重视。在一定程度上，SVM能够较好地对光伏序列进行拟合，但是由于光伏输出曲线具有强波动特性，尤其在复杂天气情况下，传统的点预测方法往往达不到理想精度［11］，因此，一种更为可靠的预测方法成为专家们探索的目标。

1.2 需要解决的问题

（1）传统SVM对核参数和惩罚系数优化过程中存在时间长、易陷入局部最优等固有缺点［12-13］。

（2）支持向量机的回归估计函数中常用的核函数有线性核函数、高斯基BRF核函数［14］等，不同核函数具有不同的回归拟合特点，如何根据光伏子序列的特点进行针对性预测，将影响最终预测结果。

（3）点预测所提供的信息非常有限［15］，无法反映光伏输出的潜在不确定性，电网调度人员无法从中得知预测值的置信区间，难以对系统的预留备用作出有效决策。

2 解决方案

相比于传统的光伏点预测，区间预测［16-18］除了能够呈现未来时刻光伏系统的预测值，还提供了该预测值的置信区间对输出功率的波动范围进行估计。显然，在调度部门制定发电计划和安全经济运行调控方面，区间预测更具实用价值。

本文提出了一种光伏出力模糊区间预测方法。针对传统SVM的固有缺陷，本文采用纵横交叉算法（crisscross optimization algorithm，CSO）［19-20］优化SVM，得到CSO-SVM预测方法；针对光伏阵列系统输出的波动特性，基于模糊信息粒化理论［21-22］将其进行模糊处理，得到UP、R和LOW三个粒子分量，分别对应光伏功率输出的波动上界、平均值和波动下界，再分别采用CSO-SVM进行预测；其中，对于波动性较大的粒子分量UP和LOW，采用高斯核函数，而较为平稳的R则使用线性核函数；最后，得到光伏输出功率的预测值及其置信区间。

2.1 模糊信息粒化

所谓的信息粒化就是根据一定的划分规则，将1个信息整体分解为多个部分进行研究，每个部分即为1个信息粒。本文采用模糊粒子化方法，基于模糊集理论对光伏数据进行模糊信息粒化处理。模糊信息粒化主要分为窗口划分和信息模糊化2个环节：窗口划分就是将整个时间序列划分为若干个子序列，每个子序列作为1个操作窗口；而信息模糊化则是根据一定模糊规则将每个窗口数据转换成一个个模糊信息粒。信息模糊化是粒化过程的重点，要使新构建的模糊集能够取代原来窗口的信息。考虑单窗口问题，即是把整个数据序列X看作一个窗口进行模糊化，X上建立模糊粒子g是模糊化的任务。模糊概念G与模糊粒子g的关系如下：

式中：x—论域X的变量；

G—以X为论域的模糊集合。

常用的模糊粒子形式有三角型、梯形、高斯型、抛物型等。由于本文主要依据光伏随机分量的波动范围进行区间预测，即需要求得窗口数据的最大值和最小值，故在此采用三角形模型粒子，其隶属函数可表示为

式中：x—论域中的变量；

a、m、b—参数，分别对应原始数据变化的最小值(LOW)、平均值(R)和最大值(UP)。

对于单窗口光伏数据，UP表示该窗口数据波动的上界；R参数表示该窗口数据变化的平均水平；LOW参数表示该窗口数据波动的下界。

2.2 支持向量机及其优化

2.2.1 支持向量机原理

在非线性回归问题上，SVM首先通过非线性函数将向量从低维空间映射到高维特征空间中：φ:Rn→Rm(m≥n)，再在高维空间进行线性回归，取得在原空间进行线性回归的效果。对于给定样本，其中n为样本容量，xi为输入向量，yi为相应的输出数据。相应的线性回归函数为

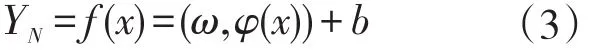
式中：φ(x)—高维特征空间向量；

ω—φ(x)的权重向量；

b—偏移量。

SVM的最优超平面可表示为以下函数的极小化问题：

式中：C—惩罚因子；ξi,ξ*i—松弛变量。为了求解式（4）最优化问题，引入Lagrange函数构造等式，即

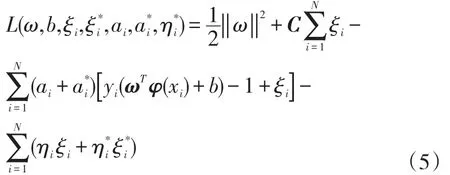
式中：ai、a*i、ηi、η*i—拉格朗日因数。

根据L的极值条件，并将ω代入式（4）可得回归估计函数的表达式为

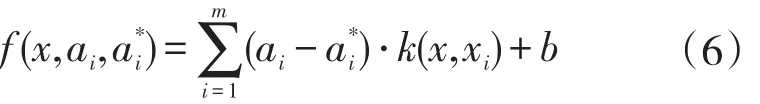
式中：k(x,xi)—核函数。

常用的核函数有线性核函数、高斯基BRF核函数等。波动较小时采用线性核函数如式（7），波动较大时选高斯核函如数式（8）。

式中：δ—核宽度。

2.2.2 SVM参数优化

预测过程中，核参数和惩罚系数的大小对算法的表现有非常关键的作用，为避免过学习或欠学习的现象，本文采用纵横交叉对SVM的参数进行优化。CSO是孟安波［19］等人提出来的一种群智能算法，该算法已经在电力系统参数优化等方面取得成功运用［19，23］。横向交叉与纵向交叉是CSO算法两个最关键的操作算子，下面分别介绍这两种操作算子。

2.2.2.1 横向交叉算子

传统横向交叉算子首先将种群的粒子进行两两不重复随机配对，然后进行算数交叉运算。本文为了保持种群中的粒子与粒子之间传递性能，将种群的粒子随机配对改为依次按序配对，创造种群中粒子与粒子之间的隐形桥梁。假设父代粒子为X(i)（i=1,2,3……N），则它们的子代粒子为

式中：c1、c2—分布在0～1之间的随机数；

r1、r2—分布在-1～1之间的随机数；

X(1,d)、X(i,d)和X(N,d)—分别是第1、第i和第N个父代粒子的第d维；

Mhc(1,d)、Mhc(i,d)和Mhc(N,d)—分别是X(i)经横向交叉产生的第d维子代。

2.2.2.2 纵向交叉算子。

纵向交叉算子的功能是对同一个粒子的不同维度进行算数交叉，假设粒子X(i)的第d1维和第d2参与纵向交叉运算，则它的子代为

式中：r—分布在[0～1]之间的随机数；

Mvc(i,d1)—粒子X(i)的d1和d2维经过纵向交叉产生的子代。

2.3 模型设计

将光伏功率数据进行模糊化处理，得到模糊粒子LOW、R和UP，并采用CSO-SVM作回归预测，从而得到预测结果：LOW’表示光伏阵列功率预测区间的下界，R’为功率输出预测确定值，UP’为功率预测区间的上界。经验证R的数据复杂度小于LOW和UP的复杂度，因此，对于模糊粒子R的预测，采用线性核函数，而其余两个模糊粒子则采用高斯核函数。预测流程如图1所示。

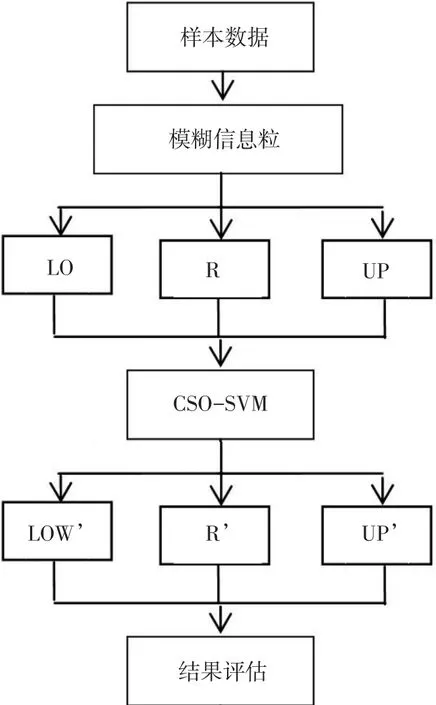
图1 光伏出力区间预测流程

2.4 实例验证

本文采用美国俄勒冈州本德一处光伏发电场（西经121.31°，北纬44.06°，海拔1 124 m，总容量3.6 kW）2011年～2013年的实测功率数据和当地气象站发布的环境数据进行模型验证，该系统的光伏功率数据每5 min采样1次。本文取每天6：30～17：30，分辨率为30 min的平均发电功率为原始光伏数据。2.4.1 区间覆盖率FICP(Forecasting Interval Coverage Percentage)［24］

式中：FICP—区间覆盖率；

N—测试样本总个数；

ξ—实际值落入预测区间的个数。

2.4.2 平均区间宽度（Interval Average Width）［24］

式中：W—平均区间宽度；

θi—第i个测试样本的置信区间宽度。W越小，表明预测效果越理想。

2.4.3 平均绝对百分比误差（Mean Absolute Percent Error,MAPE）［25］

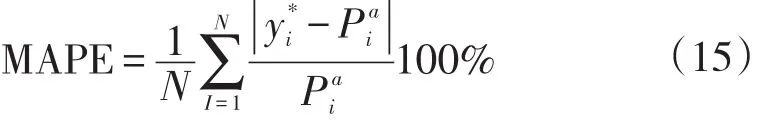
式中：预测功率值；

—实际光伏输出功率；

N—数据总个数。

MAPE越小则表明实际值与预测值的偏差越小，预测效果越好。

以2013年7月14、15和16日（其中15日、16日分别为云、雨天）为研究对象，并与以下2种模型作对比，验证本文所提模型的性能。

传统SVM法：采用传统SVM方法预测各模糊分量（即没有经过CSO优化）。

线性核SVM法：对3个模糊粒子LOW、R和UP的预测都采用线性核函数。预测结果如图2-图4所示。表1为3个模型的区间预测结果指标计算。

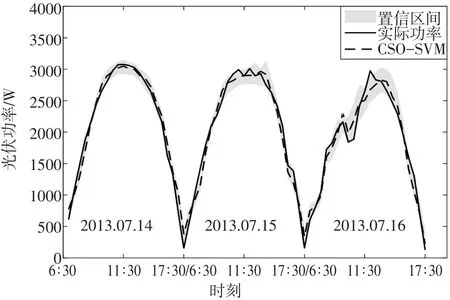
图2 CSO-SVM模型的光伏出力区间预测结果

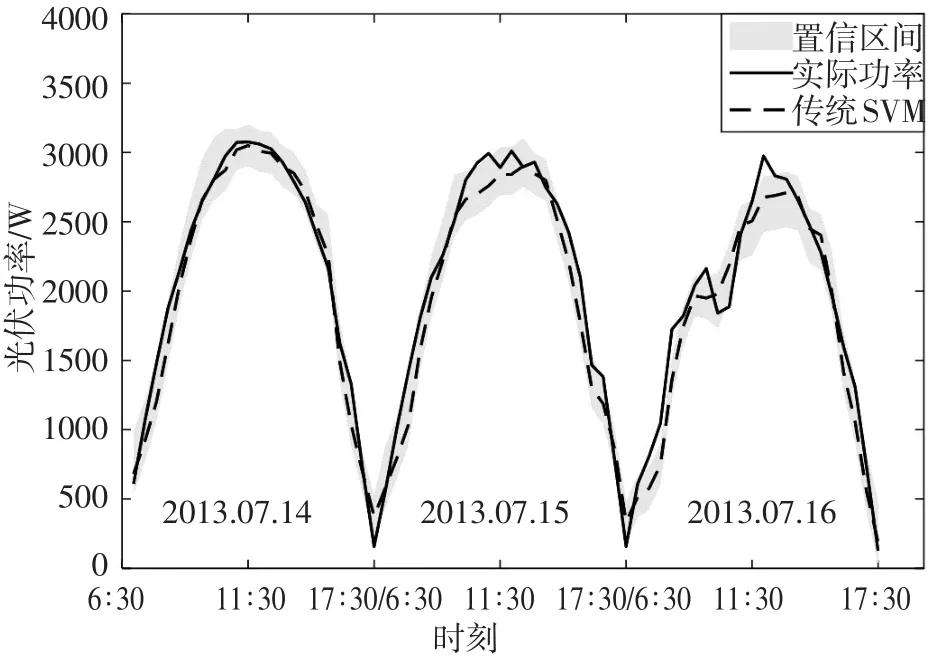
图3 传统SVM模型的光伏出力区间预测结果

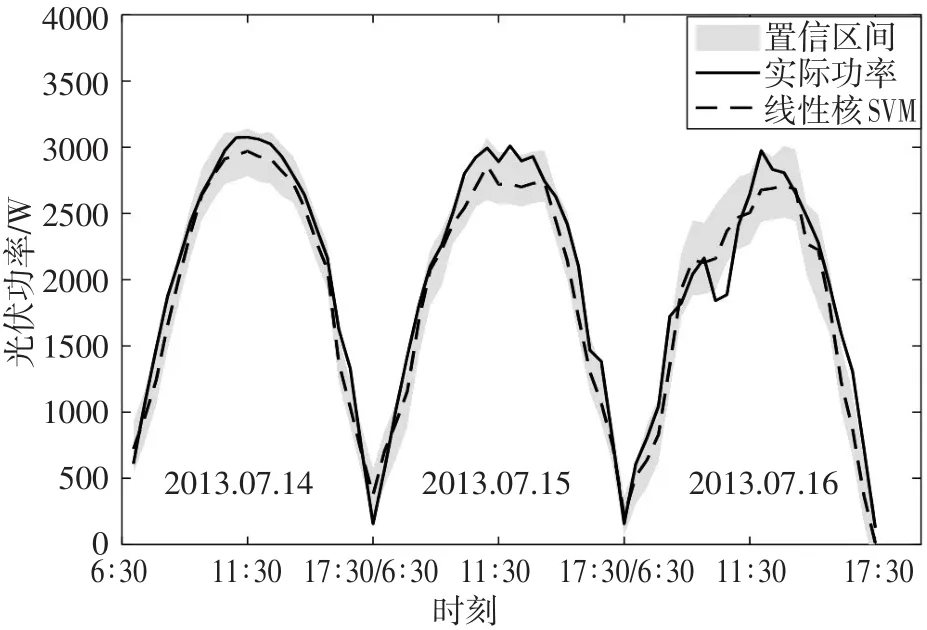
图4 线性核SVM的光伏出力区间预测结果

通过图2看出本文所提方案CSO-SVM法的光伏出力点预测值（虚线）能较好地拟合实际值（实线）。尤其在7月14日，MAPE指标达到3.56%；而属于阴天天气类型的15、16日预测精度相对略差，平均区间宽度W和区间覆盖率也稍逊，其中主要原因是阴天的光伏阵列输出波动性和随机性较强，但相比与传统SVM和线性核SVM法，本文所提的CSO-SVM法的预测效果明显优胜。对比图2和图3，显然图3所显示的实、虚线拟合度没有图2好，置信区间也较宽，从表1可知，传统SVM法的W指标皆超过200，明显大于CSOSVM法的W值；以及对比图2和图4，依然发现本文所提的CSO-SVM法具有较好的预测效果。尤其在属于阴天天气类型15、16日，本文方案具有较好的MAPE指标。

3 效果评价

（1）通过引入纵横交叉算法，对传统支持向量机的参数寻优过程做改进。其3天的MAPE指标分别为3.56%、5.61%和7.72%，显然，皆优胜于传统SVM法的4.24%、7.83%和10.13%，表明该方法有效避免了传统SVM使用梯度下降法寻优过程中所存在的缺点。

（2）根据模糊信息粒化理论，将原始光伏数据进行处理，针对不同子序列的波动特性选择相应的核函数。3天试验中，相比于本文所提的CSOSVM法，线性核SVM法有2天的MAPE指标大于10%，而本文方法3天的该指标皆小于10%，表明该方法有效提高了SVM的拟合能力。

（3）光伏数据通过模糊化处理所得的LOW、R和UP粒子，对应其波动下界、均值和上界，并分别对其进行预测，得到点预测值及预测区间。CSOSVM法的平均区间宽度皆小于200，区间覆盖率达到85%以上，2种指标皆优胜于其他2种预测对比方案。表明本文所提的模糊区间预测方法具有实用性和优越性，可以为电网调度人员提供更加丰富和准确的预测信息。

4 结论

（1）针对传统SVM在参数优化法方面的不足，本文引入CSO算法对其进行改进，有效克服了参数寻优过程易陷入局部最优等缺点，从而提高预测精度。

表1 3种模型预测性能评估

（2）本文将光伏输出功率进行模糊化处理，得3种模糊粒子LOW、R和UP，并对不同子序列采用不同的核函数进行预测。其中，对于波动性较大的粒子分量UP和LOW采用高斯核函数，而较为平稳的R则使用线性核函数。仿真结果表明，该解决方案具有合理性和可行性。

（3）本文使用模糊信息粒化理论对原始光伏数据进行处理，并进行CSO-SVM预测，最终得到点预测值及其置信区间，某种程度上解决了传统点预测结果的信息局限性。

［1］金鑫，袁越，傅质馨，等.天气类型聚类的支持向量机在光伏系统输出功率预测中的应用［J］.现代电力，2013，30(4):13-18.

［2］王守相，张娜.基于灰色神经网络组合模型的光伏短期出力预测[J].电力系统自动化，2012，36(19)：1-5．［3］杨锡运，刘欢，张彬，等．基于熵权法的光伏输出功率 组合预测模型[J].太阳能学报，2014，35(5)：744-749．

［4］丁明，王磊，毕锐.基于改进BP神经网络的光伏发电系统输出功率短期预测模型［J］.电力系统保护与控制，2012，40（11）：93—99.

［5］YONA A，SENJYU T，FUNABASHI T.Application of recurrent neural network to short-term-ahead generating power forecasting for photovoltaic system［C］.//IEEE Power Engineering Society General Meeting，Florida，USA，2007.

［6］刘文颖，门德月，梁纪峰，等.基于灰色关联度与LSSVM组合的月度负荷预测[J].电网技术，2012，36(8)：228-232．

［7］丁明，徐宁舟．基于马尔可夫链的光伏发电系统输出功率短期预 测方法[J].电网技术，2011，35(1)：152-157．

［8］代倩，段善旭，蔡涛，等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报，2011，31(34)：28-35．

［9］茆美琴，龚文剑，张榴晨，等．基于EEMD-SVM方法的光伏电站短期出力预测[J].中国电机工程学报，2013，33(34)：17-24．

［10］王晓兰，王明伟.基于小波分解和最小二乘支持向量机 的短期风速预测[J].电网技术，2010，34(1)：179-184．

［11］姚仲敏，潘飞，沈玉会，等.基于GA-BP和POS-BP神经网络的光伏电站出力短期预测[J].电力系统保护与控制，2015，43（20）:83-89.

［12］孙斌，姚海涛.基于局域均值分解和多核最小二乘支持向量机的短期风速预测［J］.太阳能学报，2013，34（9）：1567-1573．

［13］黄磊，舒杰，姜桂秀，等.基于多维时间序列局部支持向量回归的微网光伏发电预测［J］.电力系统自动化，2014，38(5):1924.DOI:10.7500/AEPS20130710005．［14］黄磊，舒杰，姜桂秀，等．基于多维时间序列局部支持向量回归的微网光伏发电预测［J］.电力系统自动化，2014，38(5):1924.DOI:10.7500/AEPS20130710005.

［15］罗明武，孙朝霞，刘强民，等.基于集对分析理论的太阳辐照度区间预测［J］.电力科学与工程，2015，31(10)：44-49.

［16］ZAKARIA Z，MASATO O，TOMONOBU S，et al.Optimal voltage control using inverters interfaced with PV systems considering forecast error in a distribution system［J］．IEEE Trans on Sustainable Energy，2014，5(2)：682-690．

［17］董雷，周文萍，张沛，等.基于动态贝叶斯网络的光伏发电短期概率预测［J］.中国电机工程学报，2013，33(S1):3845．

［18］罗明武，孙朝霞，刘强民，等.基于集对分析理论的太阳辐照度区间预测［J］.电力科学与工程，2015，31(10)：44-49.

［19］MENG A,CHEN Y,YIN H,et al.Crisscross optimization algorithm and its application[J].Knowledge-Based Systems,2014,67:218-229.

［20］彭显刚，林利祥，刘艺，等.基于纵横交叉—拉丁超立方采样蒙特卡洛模拟法的分布式电源优化配置［J］.中国电机工程学报，2015，35(16)：4077－4085.

［21］王恺,关少卿,汪令祥,等.基于模糊信息粒化和最小二乘支持向量机的风电功率联合预测建模[J].电力系统保护与控制,2015,43(2):26-32.

［22］Zadel L.A.Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J].Fuzzy Sets and System,1997,90(2):111-127.

［23］张学清,梁军,张熙,等.基于样本熵和极端学习机的超短期风电功率组合预测模型研究[J].中国电机工程学报,2013,33(25):33-40.

［24］李知艺，丁剑鹰，吴迪，等.电力负荷区间预测的集成极限学习机方法［J］.华北电力大学学报，2014，41（2）：78-88．

［25］杨明，范澍，韩学山，等.基于分量稀疏贝叶斯学习的风电场输出功率概率预测方法［J］.电力系统自动化，2012，36（14）：125-130.

Fuzzy interval prediction of photovoltaic output power

CHEN Yunlong,YIN Hao,HUANG Qiang ZHOU Yawu
(School of Automation,Guangdong University of Technology,Guangzhou Guangdong 510006,China)

Aiming at the problems that the point prediction accuracy of photovoltaic output power is insufficient and the inherent defects of traditional support vector machine(SVM)in terms of parameter optimization,puts forward a scheme of fuzzy interval prediction of photovoltaic output based on crisscross optimization algorithm(CSO)-SVM and fuzzy information granulation theory.The results show that the proposed scheme can obtain better prediction value and its confidence interval,and in a certain degree reduce the information limitation of the traditional point prediction.

interval prediction;support vector machine(SVM);fuzzy information granularization;confidence interval

10.3969/j.issn.1672-3643.2017.05.006

广东省科技计划项目（2016A010104016）；广东电网公司科技项目（GDKLQQ20152066）。

2017-07-05

陈云龙（1993），男，硕士研究生，研究方向为智能算法在电力系统中的应用。

TM615

A

1672-3643（2017）05-0039-06

有效访问地址：http://dx.doi.org/10.3969/j.issn.1672-3643.2017.05.006