梯级电站群短期水火联合经济调度优化方法

林艺城，孟安波，陈云龙

（广东工业大学自动化学院，广东省 广州市 510006）

电网技术

梯级电站群短期水火联合经济调度优化方法

林艺城，孟安波，陈云龙

（广东工业大学自动化学院，广东省 广州市 510006）

针对多约束、非线性、不可微的梯级电站群短期水火联合经济调度优化问题，在标准灰狼算法的基础上，提出了一种基于改进灰狼算法的梯级电站群短期水火联合经济调度优化方法以处理该复杂优化问题。该算法通过融入纵向交叉操作以修正狼群前进方向，改善算法的全局收敛性；采用一种新型约束处理方法，解决传统差额约束处理方式无法处置的强耦合关系变量的违约问题，提高算法的计算效率。仿真结果表明：该优化方法不仅克服了标准GWO的缺陷，且在求解质量、精度、收敛性和稳定性等方面较其它算法具有明显优势。

梯级电站群；短期水火联合经济调度；改进灰狼算法；计数淘汰；纵向交叉

梯级电站群短期水火联合经济调度（group of cascade power stations in short-term hydro-thermal economic dispatching，GSHED）是日常电力系统运行中一类重要的优化问题，尤其在当今能源短缺与物价飞涨的大背景下，快速、精确地求解GSHED问题具有可观的经济和节能效益，然而，计及各种复杂的水力和火力系统运行约束以及考虑阀点效应的GSHED问题呈现出一系列高维、多约束、非凸、非线性、不连续以及具有多个局部最优点的特性，增加了问题的解决难度。

1 研究现状及需要解决的问题

随着系统工程理论研究的日趋成熟和现代计算机技术在梯级水电站优化调度领域的不断发展与应用，各种新方法和新技术层出不穷，常见的方法分为两大类：一类是传统优化方法，主要有线性规划法［1］、非线性网络流法［2］、动态规划法［3］、拉格朗日松弛法［4］等。传统的优化方法过度依赖数学模型，并在求解时需将数学模型进行简化，且对初始解较为敏感，因此在处理此类具有复杂约束和考虑阀点效应的梯级电站群短期水火联合经济调度优化问题时容易陷入局部最优解。另一类为启发式智能优化算法，如粒子群算法［5-7］、改进差分算法［8-11］、混合遗传鱼群算法［12］、改进量子进化算法［13］、快速进化规划技术［14］、化学反应算法［15］、基于优化的教学学习算法［16］、改进类电磁机制［17］、基于遗传算法和数据分析法［18］、效益分析法［19］、互补机制法［20］等对比于传统优化方法，启发式智能优化算法对所求问题的数学模型没有特殊限制，具有强大的适应性，但这些算法在面临不可微、不连续、非凸、非线性的大规模优化问题时，仍存在容易陷入维数灾的缺陷。

灰狼算法（Grey Wolf Optimizer，GWO）是Mirjalili［21］等人于2014年所提出的新型启发式搜索算法，该算法具有结构简单、控制参数少、易于实现、有较强的搜索能力等特点，在优化领域，已被证明在计算效率和求解精度上均优于粒子群算法，但其仍存在容易陷入局部最优的缺陷，故基于该算法这一缺点的改进还有待进一步研究，因此，针对标准灰狼算法容易早熟收敛的缺陷，本文设计了一种改进的灰狼算法（improved grey wolf optimizer，IGWO），通过引入纵横交叉算法中的纵向交叉操作以协助部分维摆脱维局部最优困境［22］，修正狼群的进化方向，增强算法的全局搜索能力，并在更新狼群位置时，采取“适者生存，优胜劣汰”的竞争策略，保证整个狼群始终朝着猎物逼近，有效地提高算法的收敛速度。此外，结合梯级电站群短期水火联合经济调度部分变量之间存在强耦合关系，提出“计数淘汰法”处理无法同时兼顾满足2个存在耦合关系变量约束的解，进一步提高解的可行性与算法的计算效率。为验证所提算法的有效性，本文通过对含有4个梯级水电站和1个火电厂的短期水火联合经济调度模型进行仿真分析，验证所提算法在求解高维、非凸、非线性的梯级电站群短期水火联合经济调度优化问题时的适应性和有效性。

2 基于改进灰狼优化算法的梯级电站群短期水火联合经济调度优化方法

2.1 梯级电站群短期水火联合经济调度优化模型

梯级电站群短期水火联合经济调度是在满足各种复杂的水力和火力系统的运行约束前提下优化各电厂出力，以达到最小系统燃料费用为目标。其数学模型［13］可表述如下。

2.1.1 目标函数

在水火发电系统中，包含多个发电机组的火电厂被等效为一个能表征整体发电厂特性的虚拟电厂。以火电厂燃料费用最小为目标函数，其数学模型可表示为

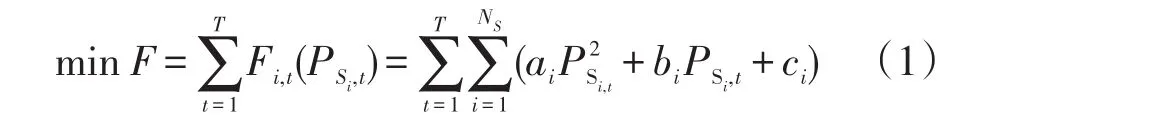
式中：F—系统总煤耗费用；

T—整个调度期间的调度时段数；

NS—火电厂数目；

ai,bi,ci—火电厂i的费用系数；

PSi,t—火电厂i在第t个调度时段的出力；

Fi,t(PSi,t)—火电厂i的燃料费用函数。

在实际的水火经济调度问题中，通常需要考虑到如图1所示的汽轮机进气阀突然开启时所出现的拔丝现象——阀点效应，该现象使得原来的二次耗量特性曲线上叠加一个正弦脉动函数，可表示为

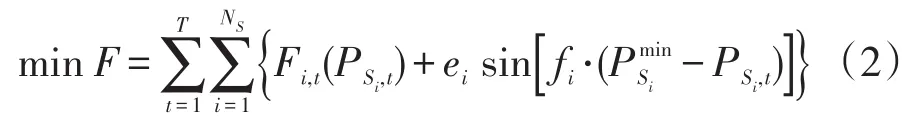
式中：ei、fi—火电厂i的阀点效应系数；

—火电厂i的最小技术出力。

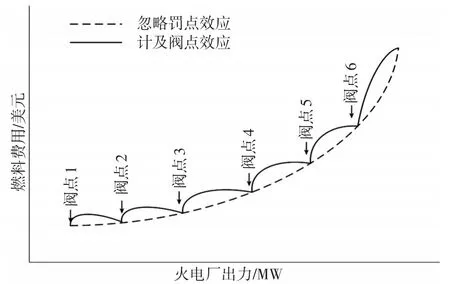
图1 计及与忽略阀点效应的火电厂耗量特性曲线对比

2.1.2 约束条件

（1）系统功率平衡约束

电力不易大规模储存，要求电力生产与消费应具备同时性，因此要保证发电厂出力与系统负荷需求实时平衡，即在整个调度期间，系统中所有发电厂的输出功率必须与系统负荷需求平衡，该约束可表示为

式中：Nh—水电站数目；

Phj,t—水电站j在第t个调度时段的出力；

PD,t—系统在第t个调度时段的负荷需求。

（2）水量平衡约束

梯级水电站的显著特点为上一级水电站发电用水及水库弃水经过一点的时滞仍可供下一级水电站使用，即上下级水电站间存在水力耦合关系。显然，水电站的当前库容不仅取决于上一调度时段的库容、天然来水量、发电流量以及弃水量，而且还取决于上一级水电站的弃、用水量，该约束可表示为

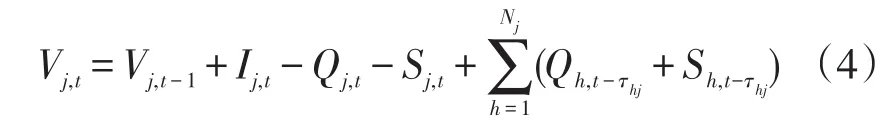
式中：j∈(1,Nh)t∈(1,T)；

Vj,t-1——第t-1个时段水电站j的库容；

Ij,t——第t个时段水电站j的天然来水量；

Qj,t——第t个时段水电站j的发电流量；

Sj,t——第t个时段水电站j的弃水量；

Nj——水电站j的上游水电站数目；

τh,j——水电站j与其上游水电站h的时滞时间。

针对平水期及枯水期在整个水电站发电优化调度阶段一般不会产生弃水，因此式（4）可简化为

（3）水电站出力

水电站的出力可被包含发电流量和库容的二次函数所表示为

式中：C1j、C2j、C3j、C4j、C5j、和C6j—水电站j的出力系数。

（4）火电厂的出力约束

（5）水电站的出力约束

（6）水库库容约束

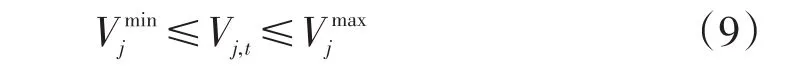
（7）水电站的发电流量约束

（8）调度周期初始库容和末端库容约束

在短期水火经济调度中，日调节水电站的调度周期较短，为合理地安排调度计划，水电站的初始库容和末端库容应严格满足预设的库容蓄水量，该约束表示为

式中：Vj,B、Vj,E—初始库容、末端库容容量。

2.2 灰狼算法基本原理

作为犬科类动物，灰狼在自然界中位于食物链的顶端，常被视为顶级猎食者；其生活方式多以群居为主，且每个狼群平均有5～12头狼，无论是日常生活还是外出捕猎，均遵循着非常严格的社会等级和任务分工制度，如α狼领导整个狼群，主要负责狩猎过程的决策制定；β狼位于第2阶层，主要协助α狼做决策；δ狼处于第3阶层，负责侦查、警戒、打围、看守；剩余狼群为ω位于最底层，服从于其它高阶层狼的命令，并开展有关的群体狩猎行动［23-24］。具体狼群等级分类及主要职责如图2所示。

图2 GWO算法狼群等级分类及主要职责

在整个算法的每次迭代中，适应度最优的个体被赋予α，次优个体被赋予β，第3名个体被定义为δ，其余个体设为ω。GWO算法仿生狼群狩猎行为过程主要包含3个步骤：包围、猎捕和攻击。

2.2.1 包围

狼群在执行狩猎任务时，首先对目标进行包围，该过程的数学模型为：

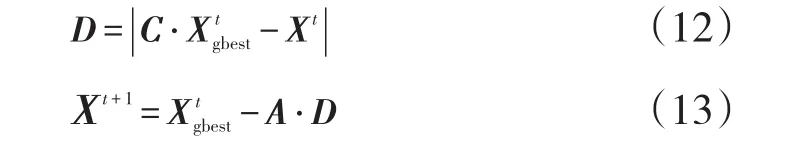
式中：t—当前狼群代数；

D—狼与猎物之间的距离向量；

A和C—摆动因子向量；

—猎物当前位置（全局最优解向量）；

Xt—狼群所在位置（潜在解向量）。

A和C的值由公式（14）、（15）计算得到

式中：r1、r2—取值范围为[0,1]的随机向量；

a—向量的值随迭代次数由2线性递减到0。

2.2.2 猎捕

在包围猎物后，狼群将执行猎捕行动，为更有方向性地搜寻到猎物的位置，该行动通常是由α、β和δ来引导，其它ω狼则依据α、β和δ的指示来更新它们各自的位置。具体更新表达式为

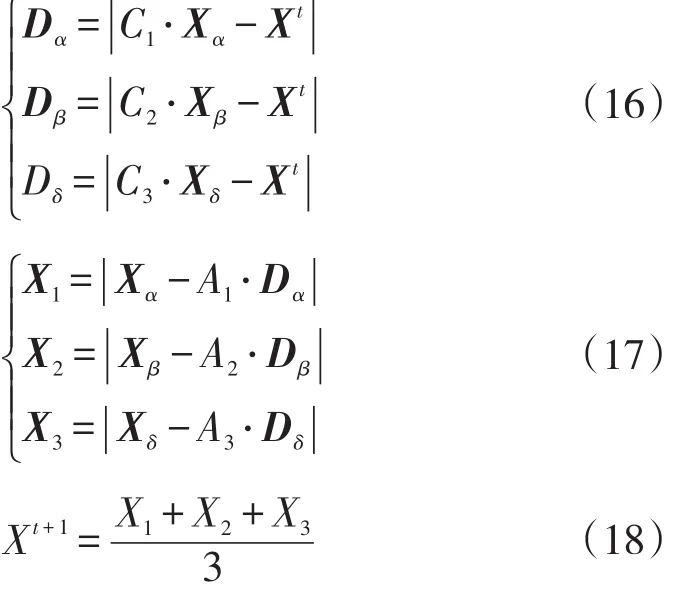
式中：Dα、Dβ和Dδ—ω狼与α、β和δ之间的距离向量；

Xt+1—更新后的狼群位置，位置更新过程如图3所示。

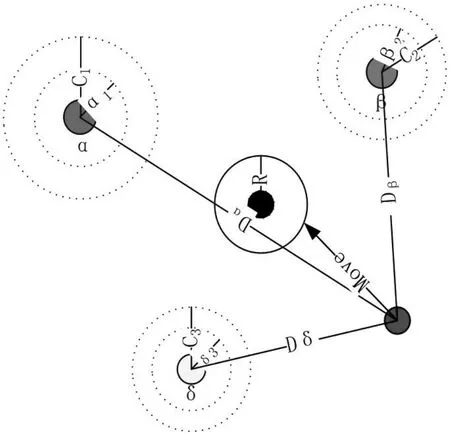
图3 GWO算法的位置更新过程

2.2.3 攻击

狼群狩猎的最后将进入攻击阶段，该阶段狼群的主要任务是完成抓捕猎物这一目标，即GWO算法获取全局最优解。该过程的实现方式主要为随着式（14）中a的值从2线性递减到0，相应地，A的值也将取得介于[- 2a,2a]内的任意数。当|A|≤1时，狼群处于集中攻击猎物的状态，而当|A|＞1时，狼群将会从猎物所在的位置逐渐分散开去，导致GWO算法失去最优解位置，进而转入到寻找其它局部最优解的过程中去，这也是GWO算法容易陷入局部最优解，且收敛时间冗长的问题所在。

2.3 改进灰狼算法

针对原始GWO存在收敛速度慢，容易陷入局部最优等缺陷，而纵横交叉算法中纵向交叉操作具有独特的摆脱维局部最优能力等优势［25］。因此，本文将借用纵横交叉算法的思想，将纵向交叉操作与竞争策略融入到标准灰狼算法，以期缓解该算法的过早熟现象，提高算法的全局收敛性。

2.3.1 竞争策略

为方便对狼群进行有选择性更新，对式（18）进行改进，即对Xt+1进行替换，如式（19）所示：

式中：MS—中庸狼个体

在捕猎阶段，为赋予狼个体一定程度的自主性，在更新狼群位置时，将如式（20）进行有竞争性的更新方式，即根据“适者生存，优胜劣汰”的进化法则，只有位置（适应度）更好的狼能够保留下来，参与下一次迭代。

由此可见，ω狼的位置除了要根据α、β和δ狼的指引外，还将保留一部分的狼自身的贪婪性，进行有选择性的更新自己的位置，因此，整个狼群在朝着猎物逐渐逼近的同时，将始终保持自身历史最优位置，这进一步加快了狼群的搜索速度。

2.3.2 方向修正操作

针对GWO算法容易陷入局部最优的缺陷［21］，而实际中早熟现象的出现可能是个体中的部分维陷入局部最优导致［25］，因此，本文将结合纵横交叉算法中纵向交叉操作解决部分维容易陷入局部最优问题的独有优势，在上述式的狼群位置更新方向的基础上，引入方向修正操作（纵向交叉操作），提供一种新的狼群位置更新方法，修正狼群的方向。

IGWO算法区别于绝大多数启发式算法的显著特点在于，方向修正操作是将狼群中可能为不同上下限或不同量纲的不同维决策变量进行算术交叉。针对不同量纲和不同上下限的不同维变量无法直接进行算术交叉的问题，在执行方向修正操作前统一对狼群中所有狼个体的每一维执行如式（21）中的归一化操作：

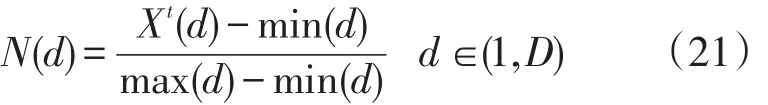
式中：D—维数；

Xt(d)—狼Xt的第d维变量；

N(d)—Xt(d)归一化后所对应的标量；

max(d)、min(d)—狼群中第d维变量的上下限。

针对狼群中可能出现部分维陷入局部最优的现象，方向修正操作采用一个方向修正概率pv来控制当前狼群中参与修正维的规模，并且每次修正仅产生一维子代，这有利于协助部分维摆脱维局部最优的同时避免破坏正常维，有效地修正狼群的前进方向。

该过程的模型构建具体如下：

假定狼群中狼个体标量N的d1,d2维分别为N(d1)和N(d2)，则对它们执行方向修正操作产生中庸狼的d1维可表示为

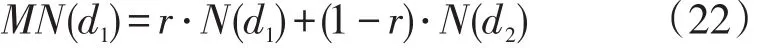
式中：d1,d2∈(1,D)；

r—0到1的随机数；

MN(d1)—中庸狼个体标量MN的第d1维。

在执行完方向修正操作后，统一对所产生中庸狼个体标量的每一维进行如式（23）的反归一化操作。

MS(d)=MN(d)⋅(max(d)-min(d))+min(d) （23）式中：MS(d)—中庸狼MS的第d维。

同理，反归一化后所得的中庸狼个体需再根据式（20）进行竞争性操作更新自己的位置，择优保留进入下一次迭代。

2.3.3 改进灰狼算法（IGWO）基本步骤

（1）设定狼群大小M、最大迭代次数maxgen、方向修正概率Pv，在解空间中随机初始化狼个体的位置，计算每个狼个体的适应度值，并选出排名靠前三只狼个体依次分为Xα、Xβ和Xδ。

（2）通过式（17）（19）优化狼群每一个体的位置，产生中庸狼，并计算其适应度，结合式（20）选择性更新狼个体的位置。

（3）对更新后的狼群执行方向修正操作，产生新的中庸狼，并计算其适应度，同理结合式（20）择优更新狼个体位置，同时根据适应度值，将狼群划分为新的Xα、Xβ、Xδ和Xω。

（4）判断是否达到最大迭代次数maxgen，若是，则输出适应度值最好的解作为最终优化结果，否则，转至（2）继续迭代搜索。

IGWO算法的流程图如图4所示。

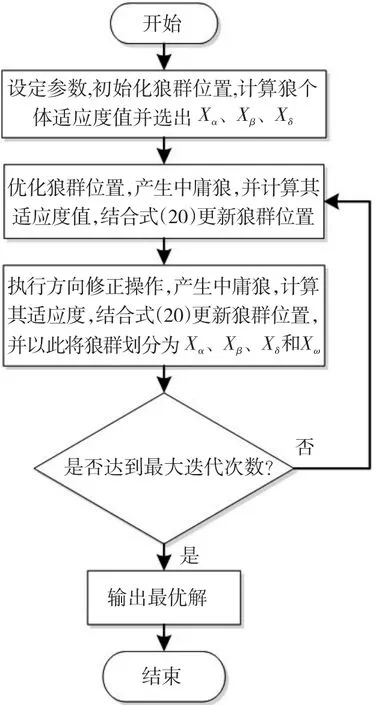
图4 IGWO算法流程

2.4 IGWO算法在梯级电站群短期水火联合经济调度中的应用

应用IGWO算法解决梯级电站群短期水火联合经济调度优化问题的具体步骤如下。

2.4.1 初始化

设置狼群大小M、最大迭代次数maxgen、方向修正概率Pv，并且采用式（24）的方式在解空间中随机初始化狼个体位置。

狼群中的每个狼个体表示一个解，针对包含Nh个水电站、NS个火电厂及T个调度时段的短期水火经济调度问题，其第m个狼个体Xm可表示为

—狼个体Xm中第t个时段水电站k的发电流量；

—狼个体Xm中第t个时段火电厂j的

出力。

2.4.2 计算个体适应度

（1）对于水电站发电流量这些决策变量，若越限，则根据式（10）进行违约处理。

（2）对于火电厂出力这些决策变量，若越限，则根据式（7）进行违约处理。

（3）由式（4）和式（9）可知水电站库容与发电流量之间存在直接的耦合关系，若越限，无法采用（1）和（2）的简单处理方式，因此本文首次采用越限计数法对其进行违约处理。

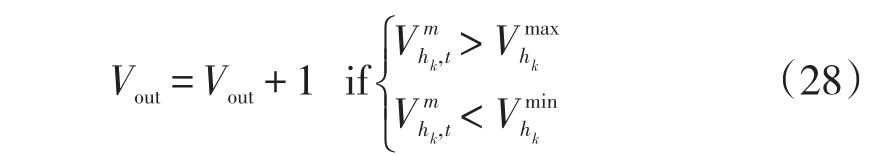
调整好的狼个体，根据式（29）计算其适应度：

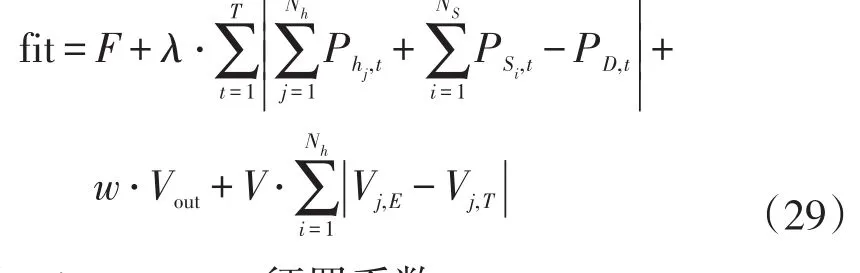
式中：λ、w、v—惩罚系数；

F—总成本，后三项分别为针对系统功率不平衡、各时段库容违约、末端库容违约的惩罚项。

2.4.3 执行狼群的包围、捕猎和攻击操作

根据式（12-17）及（19）执行狼群的包围、捕猎和攻击操作，并将式（19）产生中庸狼MS根据式（26-28）进行违约处理后代入式（29）计算其适应度，随后结合式（20）选择性更新狼个体的位置，只有适应度更好的狼能够保留下来，参与方向修正操作。

2.4.4 执行方向修正操作

针对同一狼个体的不同元素可能出现不同量纲或不同上下限的问题，因此在执行方向修正操作前统一对狼个体进行归一化操作。狼群中狼个体的所有元素进行随机两两不重复配对，并依据修正概率pv判断配对元素是否执行方向修正操作，若rand＞pv则根据式（21-23）进行修正，其次，计算所有方向修正后所产生的中庸狼MS的适应度，最后结合式（20）执行竞争策略，保留适应度较好的狼个体位置，参与下次迭代。

2.4.5 停止条件

判断是否达到最大迭代次数maxgen，若否，则转至2.4.3执行狼群的包围、捕猎和攻击操作，继续迭代，若达到最大迭代次数，则输出适应度最好的值所对应的解作为最终优化结果。

2.5 算例仿真实验分析

2.5.1 算例参数

为验证IGWO算法在求解大规模非线性特点的优化调度模型的有效性，本文将IGWO与标准GWO算法应用到含有4个梯级水电站、1个火电厂的梯级水火电力系统进行仿真分析，该梯级水火系统考虑了阀点效应、水量平衡、电力平衡约束等，调度周期为日前24 h，分为24个时段，每个时段为1 h，平水期或枯水期时包含4个水电站1个火电厂的梯级水火系统如图5所示。表1为与水电站直接耦合的上一级水电站数目及其时滞。4个梯级水电站的水电特性参数、1个等效火电厂的燃料费用参数、系统的日负荷需求等详细参数可见参考文献［9］。算例仿真采用同算法性能分析部分一致计算机运行环境。设IGWO算法的方向修正概率pv取0.5，初始种群为50，最大迭代次数为500。

图5 梯级水火电力系统

表1 耦合水电站数目及其时滞

2.5.2 仿真结果

利用前面所述的IGWO优化方法，对该梯级水火电站群短期联合经济调度模型进行优化求解，可得表2的优化结果、表3将IGWO算法和GWO算法100次独立运行所得最优解的最小值、最大值、平均值及CUP平均计算时间分别与其它不同算法的优化结果进行对比、图6给出了各水库在每个调度时段的库容情况及图7描绘了不同算法应用在该系统时的收敛曲线。

3 效果评价

由表2和图6结合文献［9］所给出的水电站参数和火电厂油耗特性参数不难看出，各调度时段无论是水电站的发电流量、水电站出力、水电站库容还是火电厂出力均严格满足各种复杂的约束条件，这种优化结果表明了前面所述的约束处理方法能有效地处理各种复杂的梯级水火电力系统安全运行的约束问题，同时不至于干扰到IGWO算法本身所固有的动态进化过程。由表3可以看出，在这一梯级水火测试系统中，采用IGWO算法取得的最小燃料费用为923 954.24美元、最大费用为925 143.54美元、平均费用为924 537.26美元以及CPU运行时间为61.31 s。虽然IGWO算法引入修改方向操作和竞争策略使得CUP运行时间相比于GWO算法增加了34.1%，然而从收敛曲线不难看出，IGWO算法在240次迭代左右便已取得比GWO算法最终优化结果更好的解，因此，与标准GWO算法相比，在相同初始种群、种群大小和迭代次数下，IGWO算法求解大规模非线性梯级短期水火经济调度优化问题时能够在相对合理的计算时间内取得更好的优化结果。此外，从表3中还可以看出相比于其它算法，IGWO算法无论是在最小值、最大值、平均值均具备明显的优势。结合图7的各算法收敛曲线对比，不难发现IGWO算法能有效地避免出现过早收敛现象，可见算法具有较强的全局收敛性。这一系列表明，改进后的灰狼算法具有较好的全局收敛性、适应性与鲁棒性，因此，相比于本文所提其它启发式算法，采用IGWO算法解决梯级电站群短期水火联合经济调度问题能取得更好的优化效果。

表2 水电站的发电流量、水火电厂出力、系统总出力

图6 水电站在调度的各个时段库容量

表3 不同算法的结果对比

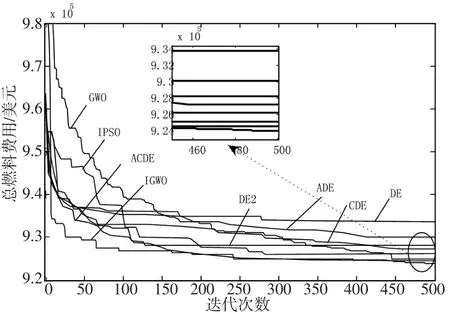
图7 不同算法的收敛曲线

4 结论

（1）所提改进灰狼算法在狼群位置的更新过程中，引入竞争策略，赋予整个狼群一定的自主性，这种狼个体始终保持自身历史最优位置，有效加快了整个算法的收敛速度。

（2）所提改进灰狼算法将纵横交叉算法中的纵向交叉操作融入GWO算法中以帮助部分陷入局部最优的维摆脱当前困局，修正狼群的前进方向，增强算法的全局收敛性。

（3）本文还根据梯级电站群短期水火联合经济调度问题所固有的变量之间存在一定的强耦合关系，首次提出计数惩罚法对符合自身约束但违背另一间接变量约束的决策变量进行“零容忍”惩罚处理，有效解决了常规惩罚方法难以处理变量存在耦合关系的问题，增强了解的可行性。

（4）所提方法在计算适应度前对各决策变量进行违约处理，减少了不可行解，提高了计算效率。

（5）采用改进灰狼算法能显著提高梯级电站群短期水火联合经济调度问题的经济性。

（6）本文所提算法目前仅研究解决单目标优化问题，下一阶段将研究该算法应用于多目标优化问题时是否也同样具备较好寻优性能。

［1］PIEKUTOWSKI M,LITWINOWICZ T,FROWD R J.Optimal short-term scheduling for a large-scale cascaded hydro system[J].IEEE Transactions on Power Systems.1994,9(2):805-811.

［2］BRANNLUND H,BUBENKO J A,SJELVGREN D,et al.Optimal Short Term Operation Planning of a Large Hydrothermal Power System Based on a Nonlinear Network Flow Concept[J].IEEE Transactions on Power Systems.1986,1(4):75-81.

［3］TANG J,LUH P B.Hydrothermal scheduling via extended differential dynamic programming and mixed coordination[J].IEEE Transactions on Power Systems.1995,10(4):2021-2028.

［4］LIU C,SHAHIDEHPOUR M,WANG J.Application of augmented lagrangian relaxation to coordinated scheduling of interdependent hydrothermal power and natural gas systems[J].Iet Generation Transmission&Distribution.2010,4(12):1314-1325.

［5］HOTA P K,BARISAL A K,CHAKRABARI R.An improved PSO technique for short-term optimal hydrothermal scheduling[J].Electric Power Systems Research.2009,79(7):1047-1053.

［6］RASOULZADEH-AKHIJAHANI A,MOHAMMADIIVATLOO B.Short-term hydrothermal generation scheduling by a modified dynamic neighborhood learning based particle swarm optimization[J].International Journal of Electrical Power&Energy Systems.2015,67:350-367.

［7］AMJADY N,SOLEYMANPOUR H R.Daily Hydrothermal Generation Scheduling by a new Modified Adaptive Particle Swarm Optimization technique[J].Electric Power Systems Research.2010,80(6):723-732.

［8］WANG Y,ZHOU J,MO L,et al.Short-term hydrothermal generation scheduling using differential real-coded quantum-inspired evolutionary algorithm[J].Energy.2012,44(1):657-671.

［9］LU Y,ZHOU J,QIN H,et al.An adaptive chaotic differential evolution for the short-term hydrothermal generation scheduling problem[J].Energy Conversion&Management.2010,51(7):1481-1490.

［10］LAKSHMINARASIMMAN L,SUBRAMANIAN S.Short-term scheduling of hydrothermal power system with cascaded reservoirs by using modified differential evolution[J].IEE Proceedings-Generation,Transmission and Distribution.2006,153(6):693-700.

［11］LAKSHMINARASIMMAN L,SUBRAMANIAN S.A modified hybrid differential evolution for short-term scheduling of hydrothermal power systems with cascaded reservoirs[J].Energy Conversion&Management.2008,49(10):2513-2521.

［12］FANG N,ZHOU J,ZHANG R,et al.A hybrid of real coded genetic algorithm and artificial fish swarm algorithm for short-term optimal hydrothermal scheduling[J].International Journal of Electrical Power&Energy Systems.2014,62(11):617-629.

［13］WANG Y,ZHOU J,MO L,et al.A clonal real-coded quantum-inspired evolutionary algorithm with Cauchy mutation for short-term hydrothermal generation scheduling[J].International Journal of Electrical Power&Energy Systems.2012,43(1):1228-1240.

［14］SINHA N,CHAKRABARTI R,CHATTOPADHYAY P K.Fast evolutionary programming techniques for shortterm hydrothermal scheduling[J].Electric Power Systems Research.2003,66(2):97-103.

［15］BHATTACHARJEE K,BHATTACHARYA A,DEY S H N.Real coded chemical reaction based optimization for short-term hydrothermal scheduling[J].Applied Soft Computing.2014,24(1):962-976.

［16］ROY P K.Teaching learning based optimization for short-term hydrothermal scheduling problem considering valve point effect and prohibited discharge constraint[J].International Journal of Electrical Power&Energy Systems.2013,53(1):10-19.

［17］郭壮志，吴杰康，陈少华，等.基于改进类电磁机制的水火电力系统短期优化调度[J].电工技术学报.2014,29(12):188-199.

［18］吴杰康，唐利涛，黄奂，等.基于遗传算法和数据包络分析法的水火电力系统发电多目标经济调度[J].电网技术.2011,35(5):76-81.

［19］吴杰康，陆文玲.基于效益分析的水火电力系统短期优化调度[J].电网技术.2009(18):25-31.

［20］杭乃善，郭小璇，郑斌，等.基于互补机制的水火电力系统短期节能发电调度[J].电网技术.2012,36(9):107-114.

［21］Mirjalili S,Mirjalili S M,Lewis A.Grey Wolf Optimizer[J].Advances in Engineering Software.2014,69(3):46-61.

［22］孟安波，胡函武，刘向东.基于纵横交叉算法优化神经网络的负荷预测模型[J].电力系统保护与控制.2016,44(7):102-106.

［23］龙文，赵东泉，徐松金.求解约束优化问题的改进灰狼优化算法[J].计算机应用.2015,35(9):2590-2595.

［24］徐达宇，Renping Liu.基于改进自组织临界优化的元启发式灰狼优化算法[J].计算机应用.2016,36(6):1588-1593.

［25］殷豪，周玉龙，孟安波.二进制纵横交叉算法在配电网重构中的应用[J].电网技术.2016,v.40;No.386(1):270-275.

Optimization method of short-term hydro and thermal power system combined economic dispatching in cascade hydropower stations

LIN Yicheng，MENG Anbo,CHEN Yunlong
(School of Automation,Guangdong University of Technology.Guangzhou Guangdong 510006,China)

Aiming at the problem of short-term hydro and thermal power system combined economic scheduling optimization for multi-constraint,nonlinear and non-differentiable cascade power station groups,on the basis of the standard gray wolf optimizer(GWO)algorithm,puts forward the optimization method of short-term hydro and thermal power system combined economic dispatching for cascade power station groups based on an improved gray wolf algorithm to deal with this complex optimization problem.The algorithm corrects the forward direction of the wolves by integrating the longitudinal cross operation to improve the global convergence.Using a new constraint processing method solves the strong coupling relation variable default problem which the traditional balance constraint cannot deal with,improves the computational efficiency of the algorithm.The simulation result shows that this optimization method not only overcomes the defects of standard GWO,but also has obvious advantages in solving the quality,precision,convergence and stability.

cascade power station groups;short-term hydro and thermal power system combined economic dispatching;improved grey wolf optimizer(GWO)algorithm;count and elimination;the longitudinal cross

10.3969/j.issn.1672-3643.2017.05.001

广东省科技计划项目（2016A010104016）；广东电网公司科技项目（CCDKJQQ20152066）。

2017-07-25

林艺城（1991），男，硕士研究生，研究方向为人工智能在电力系统中的应用。

TM727

A

1672-3643（2017）05-0001-10

有效访问地址：http://dx.doi.org/10.3969/j.issn.1672-3643.2017.05.001