超临界压力下自然循环的稳定性研究
章明德,匡 波,张项飞
(1.上海交通大学核科学与工程学院,上海 200240;2. 苏州热工研究院有限公司,广东 深圳 518002)
超临界压力下自然循环的稳定性研究
章明德1,匡 波1,张项飞2
(1.上海交通大学核科学与工程学院,上海 200240;2. 苏州热工研究院有限公司,广东 深圳 518002)
针对典型的超临界压力下自然循环回路,建立模型,分别采用基于延拓的非线性数值算法和基于频域法的matlab程序计算并判断回路的静态和动态稳定性;使用无量纲相似准则数对加热段入口温度、回路当量直径及加热段进出口局部阻力进行了参数效应分析。结果表明:静态不稳定主要发生在加热段入口温度较低的工况;回路当量直径和加热段出口局部阻力对静态稳定性影响不显著;而增大加热段入口局部阻力提升静态稳定性;动态不稳定主要发生在加热功率较高的工况,增大加热段入口局部阻力或在一定范围内增大直径可以提高回路动态稳定性;增加加热段出口局部阻力降低回路动态稳定性。使用抽样方法,在回路系统参数的可能选取范围内,综合研究了回路参数对稳定性影响,在无量纲参数空间表示计算结果,分别得到无量纲参数空间内的静态不稳定域和动态不稳定域。
超临界压力;自然循环;静态稳定域;动态稳定域;无量纲
超临界水堆(Supercritical Water Reactor,SCWR)是第四代核能系统国际论坛(Generation IV International Forum,GIF)推荐的六种第四代核能系统中唯一的水冷反应堆。其与现有的第二、三代水冷反应堆有良好的技术继承性。同时,超临界水堆还具有热效率高、经济性好,结构简单、安全性高等优点,因而受到广泛关注。
在超临界压力下,流体的比热、热容、密度、黏度等物性在拟临界点附近发生剧烈的变化,使其具有特有的传热流动特性,进而显著影响超临界压力下水系统的特性。
目前一些SCWR设计采用非能动安全系统,基于自然循环方式是其中一个重要选项。如果系统发生静态或动态不稳定现象,有可能影响SCWR的运行及安全特性,所以研究超临界压力下自然循环的不稳定性对于SCWR非能动安全系统的设计至关重要。
本文针对超临界压力下自然循环单通道回路,基于延拓的非线性数值方法,分析其静态稳定性特点;相应地,采用频域法计算分析系统动态稳定性特点;进一步地,通过数值计算及无量纲分析,探讨部分参数的不稳定性影响,并研究两种不稳定性在影响参数空间的分布规律。
1 超临界压力自然循环水动力模型的求解与静态计算程序的验证
本文针对如图1所示的典型自然循环回路进行流动稳定性研究,回路由下水平段、水平与竖直加热段、上升段、上水平段、水平与竖直冷却段、稳压器和下降段等构成。分析回路热工水力特性时,主要采用这样的简化假设:(1) 一维的自然循环流动;(2) 不计回路中因摩擦等造成的热效应,且不计流体轴向导热;(3) 加热总功率等于冷却总功率,且加热/冷却段热负荷均匀。
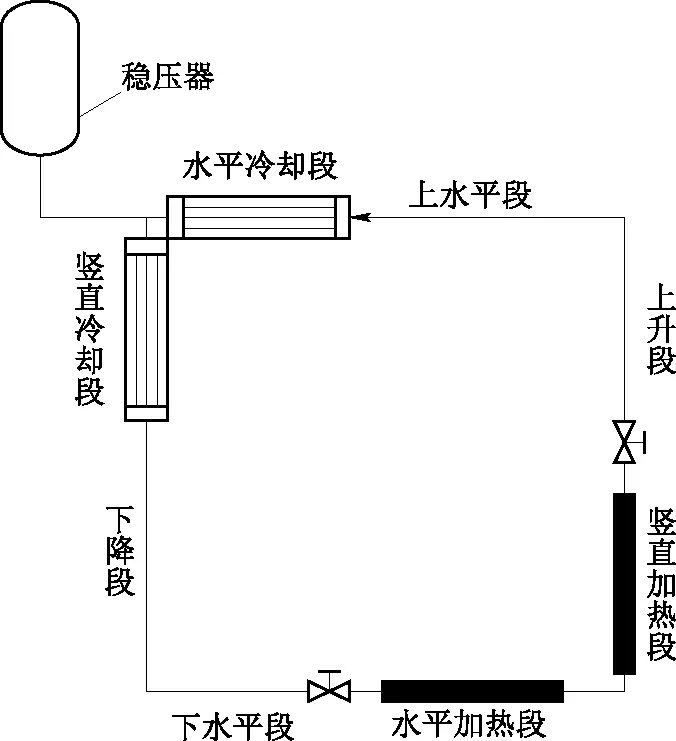
图1 典型的超临界自然循环回路Fig.1 Schema of typical natural loop under supercritical pressure
1.1 模型求解与系统静态不稳定特性
典型自然循环回路稳态热工水力行为的基本控制方程如下:
质量方程:

(1)
动量方程:
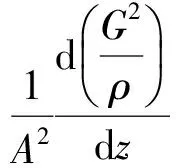
(2)
能量方程:
(3)
式中:G——回路循环流量;z——沿回路方向的一维坐标;A——流道截面积;ρ——流体密度;P(z)——回路中沿z方向的压力分布;g——重力加速度;gsinθ——重力加速度沿流动方向的分量;f(z)——沿z的阻力(包含沿程摩擦阻力ffr和局部阻力fl);q′(z)——z处加热或冷却线功率;Lc——冷却段长度;Lh——加热段长度。
将动量方程(2)沿回路积分,有:
-∮loopρgsinθdz=∮loopfdz
(4)
式(4)即回路的驱动力-阻力方程,自然循环水动力分析的核心问题是在质量方程和能量方程的约束下,求解驱动力阻力方程:
Λ(G,Q)=Fdvive(G,Q)-Fresist(G,Q)=0
(5)
对回路进行节点划分,并将Fresist表示成沿程摩擦阻力和局部阻力两部分,得到控制方程的离散化形式:
Gi=G
(6)
(7)
Gi(hi-hi-1)=q′Δz
(8)
式中:ξfr——沿程阻力系数;
ξl——局部阻力系数。
本文使用Kondrat’ev关联式计算绝热段沿程阻力系数,以Filonenko关联式计算非绝热段沿程阻力系数,详见[1]。
本文以基于延拓的非线性数值算法[2]求解驱动力-阻力方程[式(5)],获得系统各个参数条件下驱动力-阻力方程(进而得到系统的功率-流量关系)的解图,通过解图在不同区域中解的性质(单解、多解)识别出该系统参数下是否发生静态不稳定(流量漂移),其中驱动力-阻力方程或功率-流量关系多解区即为静态不稳定区。
1.2 验证
为验证模型与数值程序分析的可靠性,本文对清华大学3m×3m的超临界自然循环水回路的水动力循环特性进行计算。该回路下水平段和数值加热段内径为8mm,其他段内径32mm,回路相关参数详见[3]。计算结果和实验数据的对比如表1所示。本文共对[3]中四种工况进行了数值计算,结果显示,计算值相对于试验值的最大误差不超过2%,说明本文回路驱动力-阻力模型与分析、解图计算以及相应的非线性数值求解算法可靠与可信。

表1 计算值与实验值的对比
2 超临界压力下自然循环静态稳定性的参数敏感性影响与稳定域
2.1 超临界压力下自然循环水动力特性模型的无量纲化
基于系统模型及其静态特性的数值计算,都立国等[4]、张项飞等[5]都探讨了超临界压力下自然循环回路在一些参数工况条件下的水动力特性及参数效应。然而这些结果只能是初步演示系统稳态热工水力特性与特点,尚不能一般性地给出系统的参数影响规律,以及系统不稳定域分布。Ambrosini等[6,7]提出类似于两相流动不稳定性的无量纲分析,基于次拟临界数Nspc和拟临界转变数Ntpc等无量纲数,分析加热通道中超临界流体流动不稳定特性,值得借鉴。
本文从无量纲化的控制方程组出发,基于模化相似准则,结合模型的数值求解,在无量纲坐标下更一般性地研究超临界压力下自然循环水动力特性影响因素及静态不稳定域。
为此,定义以下无量纲数:
式中:pc——拟临界点物性;0——参考点物性(加热段入口为参考点);v——流体特征体积;L——回路总长度;Lh——加热段长度;u——流体流速;β——等压热膨胀系数。
将上述无量纲数代入自然循环回路控制方程组,可得如下相应的无量纲控制方程组:
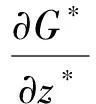
(9)
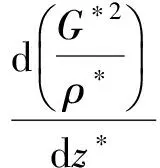
(10)

(11)
考虑上面的式子中模型与原型相比各项系数相等,即可得到相应的无量纲模化准则:(1) 拟临界转变数Ntpc:表征自然循环回路的加热特性;(2)傅鲁德数Fr:表征驱动力(浮力)与重力之比;阻力数Nf表征沿程阻力与重力之比,再加上局部阻力的影响;进一步地,可定义驱动力-阻力数Ndf,它表征驱动力、阻力和重力间的相对关系:

(12)
此外,考虑到表征加热段加热特征的需要,还定义了:(3)次拟临界数Nspc,它反映加热段入口处流体物性与该压力下拟临界物性的差异。显然,Ntpc、Nspc和Ndf既囊括了超临界压力下流体在拟临界点附近的物性特征,也涵盖了控制该自然循环回路循环流动所遵循的规律,所以这三个无量纲数可用于表征系统不稳定区域在参数空间内的分布。
2.2 超临界压力下自然循环水动力特性的参数影响
采用前述自然循环回路,本文数值计算了该典型回路的水动力特性,回路尺寸及节点划分由表2给出。

表2 回路尺寸与节点划分
2.2.1 加热段入口温度的影响
改变加热段入口温度而计算得到超临界压力下(这里为25MPa)自然循环流量-功率曲线结果如图2所示。可以看到,在一定入口温度范围内,随着入口温度降低,回路循环流动从静态稳定(无多解区)向静态不稳定(有多解区)过渡,存在一个“界限入口温度”(简称“界限温度”,即图2中的395K)。当加热段入口处温度小于界限温度时(如360K),自然循环系统可能出现流量漂移,超过这一温度,静态流量漂移现象消失。

图2 不同加热段入口温度的流量-功率曲线Fig.2 Mass flow rate vs. heating power of different inlet temperatures
由图2还可看到,随着加热功率Q增加,回路循环流量G先增至最大值Gm,然后减小。静态不稳定现象(即功率-流量关系的多解区)可能发生在Gm之后区域。Gm反映了回路的最大输热能力,其后的多解区将出现静态不稳定性,可能出现循环流量陡然跌落(流量漂移),对设备系统输传热不利,应尽量避免。
将超临界压力下自然循环静态流动特性的计算画在Ntpc-Nspc平面上(如图3所示),可以看到,在一定压力(这里25MPa)下各状态点所连成的曲线为界限温度点分成静态稳定与不稳定两段。稳定段为Nspc和Ntpc较小的部分,而不稳定段则为Nspc和Ntpc较大的部分。也就是说,加热段入口温度越高(Nspc越低),加热功率越低(Ntpc越低),则系统越趋于静态稳定。
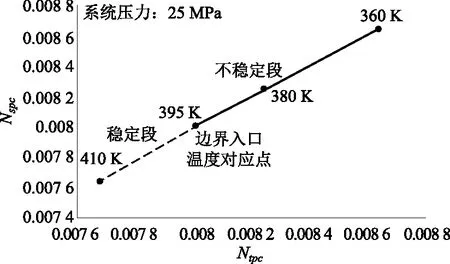
图3 不同入口温度的拟临界转变数和次拟临界数Fig.3 Ntpc vs. Nspc of different inlet temperatures
2.2.2 回路当量直径的影响
对于上述典型的自然循环回路,分别取当量直径为12mm、16mm、20mm、24mm、28mm,计算可得在25MPa系统压力下,相应的“界限温度”分别是395K、392K、390K、388K和386K。不同管径的Ntpc的变化幅度约为0.0002,而不同加热段入口温度的Ntpc的变化幅度约为0.002,Ntpc随管径变化幅度仅为随温度变化幅度的10%。可知不同加热段管径的“界限温度”和拟临界转变数变化范围均较小,所以认为回路流道当量直径对于静态稳定性的影响较小。
2.2.3 加热段进出口局部阻力的影响
本文分别在加热段入口和出口设置局部阻力,分析加热段进出口局阻的影响。在系统压力25MPa,入口温度380K时,分别设置局阻系数为0、5与10。则分别相应于加热段进、出口处不同局阻的计算结果如图4所示。

图4 不同局部阻力系数的功率-流量图Fig.4 Mass flow rate vs. heating power of different local resistance(a)入口局部阻力系数;(b)出口局部阻力系数
计算结果表明,加热段入口处局阻增加,会降低回路的循环流量与对应的加热功率,此时回路的自然循环能力降低;但是加热段入口局阻增加又会改善回路静态稳定特性,最大流量点之后流量随功率增加而降低的变化幅度明显放缓,这使得设备热负荷不至于由于流量降低增加过快,这对安全传热有好处。
而增加加热段出口处局阻,最大自然循环流量及相应的加热功率也会降低;且对于相同局阻,出口段局阻使最大自然循环流量及相应加热功率变小的幅度,明显大于在入口段局阻;但并不会改善回路的静态稳定特性。
2.3 静态稳定特性的无量纲稳定域
为一般性地考察超临界压力下自然循环静态不稳定性的发生条件,量化表征在一定范围内参数对静态稳定性的影响规律,本文选取典型自然循环回路结构(即图1中简化回路的形式),在一般运行的参数范围内(见表3),分析其稳定域分布。涉及的参数变量包括:回路高度、加入段长度、加热段进出口局阻、流道尺寸以及加热段入口温度等。因这些参数综合影响静态稳定特性,且参数组合数量巨大,本文在一定的参数范围内运用特定的分层抽样方法[拉丁超立方抽样(LHS)],抽取参数组合(目前本文取实验装置热工回路实际可能的参数范围,见表3;且设各参数为平均分布),以这些参数组合值作为计算输入,由此了解回路静态稳定特性,并以无量纲参数空间中回路的稳定域分布来反映。

表3 静态稳定域参数选取范围
在上述各参数范围内抽样选取200个参数组合,经计算,系统共在106个参数组合下发生静态不稳定。相应的静态稳定域在无量纲参数空间内的分布如图5所示。图中三角形标记代表不稳定对应的参数组合,圆圈标记表示稳定回路对应的参数组合。可以看到,回路发生静态不稳定的点位于无量纲空间内次拟临界数Nspc较大和拟临界转变数Ntpc较大的区域,相应于加热段入口温度与加热功率较高的区域,所以认为静态不稳定的主要影响因素是入口温度;虽然驱动力和阻力都是影响回路静态稳定性的重要因素,而Ndf囊扩了驱动力、阻力和重力三个因素,其反映了三者的相对关系,随工况的变化较复杂,静态稳定性在驱动力-阻力数Ndf上的分布未表现出明显的分野。
3 超临界压力下自然循环动态稳定性影响参数的无量纲分析与稳定域
3.1 超临界压力下自然循环动态稳定性判识

图5 静态稳定域的无量纲空间分布Fig.5 Distribution of static stability regime in dimensionless space(a) 静态稳定域随次拟临界数和拟临界转变数的分布;(b) 静态稳定域随驱动力-阻力数的分布
除静态稳定性外,超临界压力下自然循环水回路也会在静态工作点(定态点)处呈现不同的动态流动特性,特别地,一定条件下还会发生流动的动态不稳定性。超临界压力下自然循环流动的动态特性及其稳定性受动态控制方程组控制。采用与前类似的无量纲数,可得超临界压力下自然循环的无量纲动态控制方程组如下:
质量方程:

(13)
动量方程:
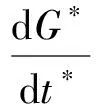
(14)
能量方程:
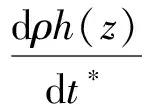
(15)
上述控制方程组最终可示为如下统一形式:
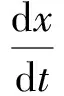
(16)
式中,A——系数矩阵;x——回路的状态参数;μ——其他系统参量;f(x,μ)——矢量场的映射函数。
由控制理论中稳定性相关原理[8],判识一定态点(Q0,G0)附近的动态稳定性,需求解系统在该点对小扰动的响应。稳定性判识方法是对定态点x0施加小扰动δx,得到扰动响应方程:
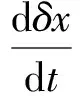
(17)
然后,由Laplace变换求解特征方程,若最大特征根的实部小于0,则流动在(Q0,G0)附近稳定,否则发生动态不稳定现象。
根据此频域法判识稳定性原理,编写了计算判识自然循环流动动态稳定性的程序,图6给出在25MPa下,加热段入口焓为800kJ/kg时(入口温度458K),一典型超临界压力下自然循环回路流动稳定性判识的结果。可以看到,对给定回路,存在一个发生动态不稳定性的“界限加热功率Qc与对应循环流量Gc,当加热功率高于该“界限功率”时,系统最大特征根实部大于0,开始出现流动的动态不稳定现象。
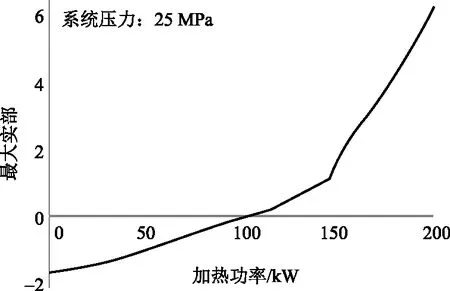
图6 不同加热功率的最大特征根实部Fig.6 Maximum real part of characteristic roots
3.2 超临界压力下自然循环流动动态稳定特性的参数影响
3.2.1 加热段入口焓的影响
对上述同样的回路,以不同加热段入口焓,计算得到其对界限加热功率Qc的影响(如图7所示)。可以看到,界限加热功率随入口焓增加先减小后略有增大。用Nspc和Ntpc表示,可得到图8所示的Nspc-Ntpc无量纲平面内动态不稳定边界。与静态不稳定仅发生在最大循环流量点之后某个很窄区域不同,动态不稳定在最大循环流量点前后区域都可能发生;入口焓(在压力一定时,即对应一定入口温度)越高,越有可能发生。
3.2.2 回路当量直径的影响
分别取当量直径8mm、10mm、12mm、14mm、16mm、18mm、20mm,计算不同直径的“界限加热功率”对应的Ntpc,如图9所示,发现Ntpc随着管径的增加先增加后减小,Nspc-Ntpc无量纲参数平面内对应的动态稳定区面积先增大后减小。

图7 不同入口焓的界限加热功率Fig.7 boundary power of different inlet enthalpies
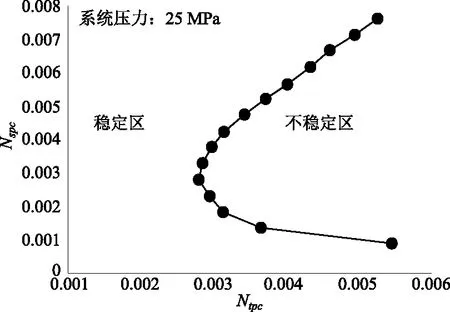
图8 无量纲参数表示的动态不稳定边界Fig.8 Stability Boundary presented by dimensionless parameters

图9 Ntpc随当量直径的变化Fig.9 Ntpc vs. diameter
3.2.3 加热段进出口局部阻力的影响
分别在加热段进出口分别设置局部阻力系数0、1、3、5,对比界限加热功率点和最大循环流量点,如表4所示。可知,加热段入口局部阻力越大,“界限加热功率”与最大循环流量功率之比Qc/Qm越大,动态不稳定的起始发生点后移,回路的动态稳定性增强;加热段出口局部阻力越大,Qc/Qm越小,动态不稳定的起始发生点前移,回路的动态稳定性减弱。
3.3 动态稳定特性的无量纲稳定域分布
为一般性地、量化地考察表征诸影响因素对超临界压力下自然循环动态不稳定性发生的影响,类似于静态不稳定域研究,在一定参数范围内随机抽取参数组合,综合分析动态稳定域在参数空间中的分布规律。本文选取如表5所示的范围进行计算参数组合的抽样,共抽取200组参数组合。计算得到图10所示的系统回路动态稳定性在无量纲参数空间内分布规律。其中,三角形标记代表不稳定点对应的参数组合,圆圈标记表示稳定点对应的参数组合。可以看到,超临界压力下自然循环流动发生动态不稳定性发生的区域主要集中在无量纲空间拟临界转变数Ntpc相对较大区域,即对应于加热功率较高的工况。

表4 动态不稳定边界点随局部阻力系数的变化

表5 动态稳定域参数选取范围

图10 动态稳定域的无量纲空间分布Fig.10 Distribution of dynamic stability regime in dimensionless space(a) 动态稳定域随次拟临界数和拟临界转变数的分布;(b) 动态稳定域随驱动力-阻力数的分布
4 结论
本文针对超临界压力下典型自然循环,采用非线性数值方法,判别自然循环静态不稳定特性及相关参数影响规律;同时运用频域法,分析动态不稳定特性及参数影响规律;此外,在无量纲参数空间内,综合研究相应的静态和动态不稳定域分布;主要结论有:
(1) 超临界压力下自然循环有一个最大循环流量Gm,相应加热功率为Qm。当功率Q大于Qm时,可能出现静态不稳定。在系统压力与回路结构给定的情况下,存在一个“界限入口温度”,当加热段入口温度小于该温度,可能出现静态不稳定。综合而言,静态不稳定性区域在三维无量纲空间中集中分布在次拟临界数Nspc和拟临界转变数Ntpc都较大的区域。
(2) 在系统压力与回路结构给定的情况下,存在一个“界限加热功率”Qc,当加热功率大于该功率时,将出现动态不稳定;Qc可能大于Qm,也可能小于Qm。综合而言,动态不稳定性区域在三维无量纲空间中集中分布在拟临界转变数Ntpc较大的区域。
(3) 主要参数对稳定性的影响:
对于静态稳定性,增加回路当量直径,提高回路自然循环能力但对稳定性影响较小;增大加热段入口处局部阻力提升回路静态稳定性;增大出口处局部阻力对静态稳定性影响不显著。
对于动态稳定性,在一定范围内,稳定性随当量直径的提高而增强;增大加热段入口处局部阻力提升回路动态稳定性;增大出口处局部阻力不利于回路动态稳定。
[1] Igor Pioro,Romney B. Duffey,Tyler J. Dumouchel. Hydraulic resistance of fluids flowing in channels at supercritical pressure[J]. Nuclear Engineering and Design,2004,231:187-297.
[2] 库克切克,马克雷. 分岔理论和耗散结构的计算方法[M]. 北京:科学出版社,1990.
[3] Yu Jiyang,Che Shuwei,Li ran, et al. Analysis of ledinegg flow instability in natural circulation at supercritical pressure[J]. Progress in Nuclear Energy,2011,53:775-779.
[4] 都立国,匡波,顾汉洋,等.超临界压力水循环系统非线性水动力特性研究[J]. 核动力工程,2009,30(2):21-26.
[5] 张项飞,匡波,胡尚武,等.超临界压力下自然循环的静态特性[J]. 电力与能源,2012,33(3):245-250.
[6] Debrash Seth Kofi,Ambrosini Walter,Chen Yuzhou. Discussion on the stability of natural circulation loops with supercritical pressure fluids[J]. Annals of Nuclear Energy,2013,54:47-57.
[7] Ambrosini Walter,Sharabi Medhat. Dimensionless parameters in stability analysis of heated channels with fluids at supercritical pressures[J]. Nuclear Engineering and Design,2008,238:1917-1929.
[8] 王永骥,王金城,王敏. 自动控制原理[M]. 北京:化学化工出版社,2015.
StudyontheStabilityofNaturalCirculationUnderSupercriticalPressure
ZHANGMing-de1,KUANGBo1,ZHANGXiang-fei2
(1.School of Nuclear Science and Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.Suzhou Nuclear Power Research Institute,Shenzhen of Guangdong Prov. 518002,China)
A typical hydrodynamic natural circulation loop under supercritical pressure is modeled to analyze the instability behavior. The static stability is calculated through a nonlinear numeric algorithm while the dynamic stability is calculated through a program based on frequency domain method. The results are presented in the form of dimensionless numbers. Influential parameters and their impacts on instability are calculated and discussed. The major factors include inlet temperature,diameter of the loop and local resistances at the inlet and outlet of heating section. According to the results,static instability phenomenon is observed when the inlet temperature of heating section is relatively low. Diameter of the loop and local resistance at the outlet of heating section have relatively little influence on the static stability while increasing local resistance at the inlet helps to stabilize the loop to the static instability aspect. Dynamic instability is observed when the heating power is relatively high. Local resistance at the inlet of heating section helps to stabilize the loop while local resistance at the outlet makes the loop dynamically instable. The increase of diameter in a certain rage can also improve the dynamic stability. According to practical conditions of engineered test facilities of natural circulation,the possible ranges of affecting parametric factors are proposed. Sets of parameter combinations are acquired through a stratified sampling method,namely LHS(Latin Hypercube Sampling),for stability calculation input. And as a result of instability calculations,a static stability regime and a dynamic stability regime of are preliminarily figured out and studied.
Supercritical pressure;Natural circulation;Static stability regime;Dynamic stability regime;Dimensionless
2017-09-11
章明德(1992—),男,江苏人,硕士研究生,从事反应堆热工水力及安全分析研究工作
匡 波:bkuang@sjtu.edu.cn
TL33
A
0258-0918(2017)06-0920-09

