数学解题中对化归思想的运用

◎张雯倩

数学解题中对化归思想的运用

◎张雯倩

数学学习是为了将理论知识和思维方式使用在实际中，这是高中学习阶段中十分关键的一门学科。我们在对其进行学习的时候，需要将相关的知识点有效地运用在解题中，这样才达到了学习的真正目的。化归思想是我们进行数学解题时常用的一种思想，其能够让复杂的问题变得简单化。本文就在实际例题的基础上，详细地阐述化归思想在数学解题中的实际运用。

和初中数学相比，高中数学涵盖范围更广，其知识更加深入。我们在学习时总是感到其存在一定的难度，对有些概念知识无法进行全面的掌握，这样就让我们进行解题时存在阻碍。而将化归思想使用在数学解题中，能够让题目更加简单，进而提升我们的解题效率。

化归思想在数学解题中的作用

在化归思想中的化就是变化原问题，转化原问题；而归则是变化、变换原问题。这是一种在高中数学解题中常用的方式。从具体的情况来看，化归思想能够把复杂的问题进行有效的变换转化，使其成为更加简单的问题；把难度高的问题经过变换转化成容易问题；把未能够解决的问题经过变换转化为已解决的问题。在这其中也可以是形式上的转换。例如命题之间的转化、数与形的转化、空间向平面的转化以及多元向一元转化等等，这些都是转化思想具体体现。我们在学习数学的时候，要将相关的知识和解题方式合理的使用在解题过程中，在解题中将化归思想溶入进去，进而掌握更多的学习与解题技巧。在对数学题进行解答的时候，我们经常会遇到一些直接求解困难的问题，经过观察、分析以及联想等相关的思维过程，或者依据已存在的学习经验，选用合理的方法进行变换，把原来问题转化成新问题。经过对新问题求解，进行实现解决原问题的目的，这种思想方式是化归与转化思想的核心。在不断的学习与练习过程中，我们可加强对化归思想的运用，使其融入到解题思路中，进而有效的提升自己的解题效率。

化归思想在数学解题中的具体运用

在常量问题中的运用

在对高中数学进行学习的时候，我们已经习惯与把x当做任何方程式中的变量，这是一种固定性的思维。但是在某些问题中，将x当做变量的思维会让解题过程遇到阻碍。所以我们要在数学解题中灵活的运用化归思想，把式子中的变量当做常量，把常量作为变量，以此开阔自己的解题思路。就常量和变量进行转化的问题，将下面这道问题作为例子：

例题1：目前已知实数p满足|p|≤2，其中包含有p的不等式x2+px+1＞2x+p恒成立，求出x取值范围。

解析：我们在解答这道题目的时候，极易将题目认为含有变量x和常量p的不等式求解，若是使用这种思想进行解题，则就会存在很大的难度。若是使用化归思想，把式子中的x作为常量，把p当做变量，则就能够让问题更加简单。其具体过程是把原式子化为有关p的一元一次不等式p（x-1）+（x-1）2＞0，然后得出f（p）=p（x-1）+（x-1）2。这样就能够把原式子转换成为一元一次不等式，之后解答出x＜1。经过对这个例题的解答，我们就能够知道把常量问题转换成为变量能够更加轻松地解题。

在几何问题中的运用

将化归思想使用在几何相关的问题中，使用分割、变形以及展开等相关方式，绘制辅助线对空间平面图形进行处理，进而把立体问题化归于平面问题，这是我们在解答立体几何问题时常使用的方式。

例题2：就图1所示，正三棱锥P-ABC中，各个棱商都是2，其中E为侧棱PC的重点。现在有一只蚂蚁在A点出发，经过侧面PAB与侧面PBC到E点，试着求出蚂蚁走过的最短距离。

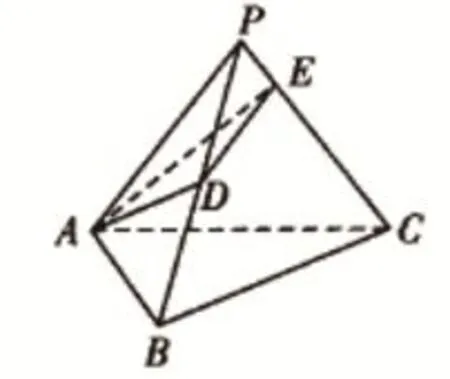
图1

解析：在解答这个问题的时候，我们都知道平面上两个点距离最短。在对三棱锥中两个点最短距离进行求解时，可以将图形展开，这是将立体几何化作平面问题的基础，经过展开之后如图2。

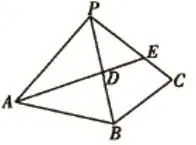
图2

经由平面中两点距离最短可知，其中最短距离是线段AE，在三角性PAE中，PA=2，PE=1，且∠APE=，由余弦定理获得AE=。通过这个问题的解答我们就能够知道将立体图展开，其实际上能够让空间图形中一些不容易发现的几何体出现，将相关的元素位置关系与数量关系呈现出来。

在函数问题中的运用

函数是高中数学知识中关键的构成部分，将化归思想使用在函数解题中能够衍生出几种方式。其一，函数中动和静的转化，使用化归思想把处在静态的量构成动态的函数形式，依据函数运动特点对实际例题进行解答。

解析：我们在解答这道题目的时候，就能够使用函数中动静相互转换的形式进行解答，将这两个数量的函数进行构建，经过对比函数图象的模式，最后得出这个结果。还有则是函数中数与形以及转换成为根的解题方式，这些都是将化归思想使用在函数中的常用方式。

数学的学习能够有利于我们思维逻辑的培养，将相关的理论知识使用在解题过程中能够提高自己运用知识的能力。作为数学解题中常用的一种思想方式，化归思想能够有效的简化数学难题，开拓我们的的解题思路，进而正确有效的解答题目，提升自己数学学习能力。

长沙市麓山国际实验学校）