粒子群蚁群融合算法的火灾救援路径研究
李怡弘,裘 炅
(杭州电子科技大学 计算机学院,浙江 杭州 310018)
粒子群蚁群融合算法的火灾救援路径研究
李怡弘,裘 炅
(杭州电子科技大学 计算机学院,浙江 杭州 310018)
为获取最优的救援路径,以提高救援的有效性和实时性,文中提出了一种粒子群蚁群融合算法。该算法在分析影响路径选择因素的基础上,运用模糊数学中的层次分析法评定了道路的权重,建立了消防灭火救援模型;使用粒子群算法快速获取次优解,将此次优解作为蚁群算法的初始信息素增量,并将求解出各段路径权重矩阵引入到优化后的蚁群算法状态转移概率的求解模型中来,再利用这种改进后的状态转移规则,且考虑行车速度时变性的基础上求解出模型的最优解。实验结果表明,该方法可以完成最佳救援路径的规划。
粒子群算法;蚁群算法;融合算法;优化;救援路径
火灾危害严重,且随着社会经济的发展,火灾事故发生概率递增,严重的威胁着公共安全和人们的生命财产安全[1]。当火灾发生时,救援时间是影响火灾救援工作的关键因素[2],而消防车辆到达现场所需时间与其所选择的路径是有紧密联系的。因此,如何合理规划救援路径就显得尤为重要。目前,常用的路径规划方法有:蚁群算法、遗传算法、神经网络算法、粒子群算法等智能仿生法[3]。不同的路径规划方法有着各自的优缺点:遗传算法全局搜索能力强,但算法容易“早熟”,陷入局部最优,且算法编程实现比较复杂,搜索时间较慢[4];神经网络法具有高度的并行性,收敛速度快,但是其求解速度慢且在求解过程中需要非常详尽的数据才能实现路径规划[5];蚁群算法是一种全局启发式的算法,具有良好的信息反馈机制,可以分布式并行计算,且启发式搜索能力较强,但是由于初始信息素匮乏,使得初期运算速度慢[6];粒子群算法概念简单、易于实现,需调整参数较少,初期收敛速度快,具有较强的全局搜索能力,但后期局部搜索能力差,易陷入局部最优[7]。
基于上述描述,本文提出将粒子群蚁群融合算法作为火灾救援路径规划的求解算法。融合算法结合粒子群算法初期易收敛、搜索速度快和蚁群算法搜索精度高的优势,从算法的效率和求解质量上都有了很大的提高。针对实时的交通路况,本文引入道路权重的概念,根据路程距离长度、道路交通量、道路路面状况和天气状况四个因素[8]采用层次分析法获取各个路段的权重,将此作为融合算法中路径选择的依据。最终算法结合火灾发生时刻各段道路的实时行车速度,找到一条时效性最高的灭火救援路径。本文充分考虑了在火灾发生时刻影响消防车辆调度的一些客观因素,并在算法求解时结合调度高时效性的特性。因此,该方案具有一定的现实参考意义。
1 相关问题概述及模型建立
1.1 基于层次分析法的道路权重评定
本文采用定性与定量相结合的层次分析法AHP(Analytic Hierarchy Process)来确定各个影响因子的权重。首先将交通流量、路径距离、道路等级、天气状况作为路段权值的4个影响因子,结合AHP原理构造一个2层结构:目标层Z和准则层A。如图1所示,Z层的权重用W表示,A层的权重分别用w1,w2,w3,w4表示。
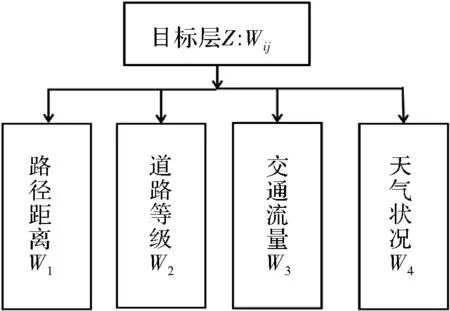
图1 路段权重因子模型
然后根据文献[9]以及AHP计算步骤可计算得出各个影响因子的权重即w1,w2,w3,w4的值为W=(0.5848 0.1320 0.1320 0.1513)。
1.2 数学模型建立
1.2.1 基本假设
(1)已知消防站点(消防车辆出发点)和火灾现场的具体位置;
(2)对于消防车辆,在消防站(车辆起始点)出发时无停顿时间,即消防车辆充足,接到调度指令立即出发;
(3)本文讨论的火灾救援只讨论从单一起点(消防站点)到单一目的地(火灾现场)问题;
(4)消防车辆在行驶过程中,整个区域内的设施固定,即建筑物位置、大小,道路位置等保持不变;
(5)本文不考虑从接到火灾报警到调动消防人员的过程;
(6)行驶速度不考虑车辆行驶的方向,即正向和反向是一致的;
(7)在已经划分好的时间段内,消防车辆的在设定的路段内速度不变。
1.2.2 建立数学模型
本文研究的目标是:如何在火灾发生后以时间为优化目标找到一条从消防站点到达火灾现场的最优路径。假设有向图G(V,E),V代表有向图G中路径上的节点集,即V={v1,v2,…,vn},v1,v2,…,vn代表了G中的建筑物,本文规定,v1代表消防站点,vn代表火灾现场;E代表有向图G中节点之间的路径集,E⊆V×V表示可行路径总和,设置R为v1到vn的所有可行路径总和,R∈E;P为其中的某一条路径,P∈R;(vi,vj)∈E代表从节点i到节点j之间的路程,e(vi,vj)=ωij代表节点i到节点j之间的权值。ωij的计算可结合上一节AHP中各个影响因子权值的评定,得到
ωij=tij+sij/(vij×ω1)(ω2×rij+ω3×fij+ω4×wij)
(1)
其中,w1,w2,w3,w4为AHP中获得的各因素的权重系数;sij代表vi到vj之间的距离;vij代表v1到vn之间的平均速度;r、f、w分别代表道路等级、交通流量和天气因子。tij表示从vi到vj之间所需的时间。由于不同时间内通过某一路段的速度不一样,为了更加准确贴近实际情况,增加算法可靠性,本文以天为划分的粒度,将一天24 h分为几个时间段来分别表示当前时段内的速度情况:T0 其中,lij代表v1到vn距离的长度。 设ω(P)为v1到vn所有路段的权值总和,即有 ω(P)=∑ωiji,j∈(1,…,n) (2) 因此,要求找到一条从消防站v1到火灾现场vn的路径使得式(3)成立 (3) 道路的权值越小,救援时间就越短,图2为救援路径规划模型。 图2 救援路径规划模型图 粒子群优化算法[10](Particle Swarm Optimization,PSO)首先初始化一群随机粒子,然后通过多次循环迭代搜索到最优粒子。在每次迭代过程中,粒子先获取个体极值pbesti(到目前为止粒子自身搜索到的最优位置)和全局极值gbesti(到目前为止粒子群中搜索到的最优位置),然后利用式(4)和式(5)更新每个粒子的速度和位置,从而引导粒子向最优解方向移动 (4) (5) 蚁群优化算法ACO[11](Ant Colony Optimization)是由意大利学者Dorigo M提出的一种模仿蚂蚁觅食的新兴群智能算法。一群蚂蚁在寻找食物的过程中,沿途中会释放一种叫做信息素的化学物质。一条路径上经过的蚂蚁越多,该路径上留下的信息素也越多,其他蚂蚁能感知这种信息素并朝信息素较浓的位置移动。信息素越浓的路径,蚂蚁选择的概率越大,最终蚂蚁找到到达食物的最短路径。ACO算法用于求解组合优化问题时有两大步骤:路径构建和信息素更新。本文就这两大步骤分别对算法进行优化。 2.2.1 概率选择机制优化策略 在构建路径时,蚂蚁利用状态转移规则来选择下一个节点[12]。基本蚁群算法中蚂蚁选择下一个节点是依据四周路径上信息素的浓度[13],失去了探索新路径的可能,因此,本文在原有的概率选择机制基础上,新增一种“随机”方式,这样不仅能有效避免算法陷入局部最优,而且也更加符合蚂蚁个体的行为。并且,在此基础上引入本文中所述的道路权重概念,得到新的概率选择机制优化策略如式(6)所示 (6) 其中,[ωij]代表路径i和j之间的权重;q是在0~1区间内随机获取的值;q0和q1都是设定好的在区间0~1之间的固定值。文中设置q0=0.6,q1=0.8。 概率选择机制优化策略的设计在一定程度上增加了解空间的多样性,从而提高了蚂蚁找到最优路径的概率,而且引入道路权重后的概率选择机制将实时道路情况作为路径选择的参考指标,对算法在合理性和效率上都有一定的优化作用。 2.2.2 信息素更新机制 本文提出的信息素更新机制包括两个方面:动态局部更新和带调节因子的全局更新。 动态局部更新:由于ACO算法全局更新信息素机制在蚂蚁寻径过程中具有一定的时延性[14],因此,本文提出一种新的动态局部更新机制,该机制打破ACO算法中一次迭代结束后再更新所有路径上的信息素的方式,而采用“走一步,更新一次”的策略,更新为式(7)~式(9)。 τij(t+1)=(1-ξ)τij(t)+ξΔτij (7) (8) (9) 在上述公式中:蚂蚁数量为m,Q为常数;ξ为局部信息素挥发因子,蚂蚁k在迭代中已走过节点数为x;蚂蚁k在迭代中已走过节点间距离为dl;Lz为m只蚂蚁在迭代中走过的总距离。 动态局部更新机制保证了若蚂蚁经过某路径时信息素时实时更新,为后期蚂蚁的搜索提供了一定的指导性,减少了蚂蚁的搜索时间,提高了算法性能。 带调节因子的全局更新:传统ACO算法的全局更新机制无法加快收敛速度从而提高搜索效率[15]。因此,本文提出一种带调节因子的信息素更新机制。首先,蚂蚁在完成一次迭代后,对迭代过程中找到的所有路径根据路径长度进行排序,然后将排序得到的中间值作为标准,判断该路径是否需要更新信息素。更新信息素公式为 (10) (11) (12) 在式(10)~式(12)中,θk为调节因子;Lk为所有蚂蚁在迭代中走过的总距离;Lmid所有蚂蚁在迭代中走过的距离的中间数值;Lbest为所有蚂蚁在迭代中的最优路径长度。 新的全局更新策略的思想是使“优的路径更优,差的路径更差”,迅速将蚂蚁集中在较优路径上,加快了算法的收敛速度,减少搜索时间。 本文先使用PSO快速找到一条次优路径,并将此次优解作为ACO的初始信息素增量,然后根据式(15)得到ACO的信息素初始分布量,最后采用优化后ACO对路径寻优,以此得到最优路径 τs=τc+τp (13) 在式(15)中,τp为PSO初次寻优后得到的解转化为的信息素增加值;τc为融合前的蚁群算法的初始值常量;τs为蚁群算法搜索前的信息素初始值。 图3 融合算法流程图 算法实现步骤: 步骤1PSO和 ACO参数初始化。设置算法中参数的初始值,其中令时间t=0;循环次数Nc=0;最大循环次数设为NCmax;初始化信息量τij(0)=τ0; 步骤2获取粒子适应度值。根据适应度函数计算出每个粒子的适应度值,并以此为依据来判断该粒子是否为当前最优粒子; 步骤3更新pbest个体极值。将pbest值与每个粒子在步骤2中获得的个体适应度值比较,若粒子的适应度值>pbest值,则将该适应度值作为最新的pbest值保存,否则,则pbest值保持不变; 步骤4更新gbest全局极值。将gbest值与步骤2中获得的全局适应度值比较,若粒子的适应度值大于gbest值,则将该适应度值作为最新的gbest值保存,否则,gbest值保持不变; 步骤5更新速度V与位置x。根据式(4)~式(6)更新每个粒子的速度与位置; 步骤6返回步骤2,继续执行,直到算法达到最大迭代次数或输出最优解,此时执行步骤7; 步骤7利用PSO得到的最优路径,根据式(13)进行ACO的信息素初始化; 步骤8首先设蚂蚁的数量m,并放置在起始点。然后将这个起始点位加入到最新禁忌表tabu(s)中,其中tabu(s)里存放着蚂蚁已经过的点位,表示不可行节点; 步骤9判断蚂蚁的数量,如果>0,则执行步骤10;否则,跳转至步骤15; 步骤10增加蚂蚁数目k=k+1; 步骤11首先获取下一步可行节点集,然后根据公式(8)的状态转移规则来计算每一个可行节点的概率值,选择概率最大的节点,并将此节点加入到tabu(s)中; 步骤12更新蚂蚁数目; 步骤13判断蚂蚁的状态。如果k 步骤14局部更新。只要蚂蚁移动一步,即根据式(7)~式(9)进行局部范围内的信息素更新,并执行步骤9; 步骤15全局更新。当蚂蚁完成一次迭代后,计算本次所有路径中最优解的路径长度,并根据式(10)~式(12)更新所有路径上信息素浓度。与此同时,根据迭代次数判断是否要结束算法,当NC 步骤16得到算法的最优解,输出对应路径,至此,算法结束。 为了验证优化后粒子群蚁群融合算法的效果,进行了仿真实验。蚁群参数分别为m=100,Nmax=50,α=1,β=2,Q=100,挥发率ρ= 0.1,信息素初始值为10。粒子群的参数分别为: 粒子数目30。 最大迭代次数为50,c1=c2= 2,w=0.9,Vmax=10。 本文使用图5中的路网图进行描述。其中,A~R节点代表建筑物,1~28代表两节点之间的可行路径。假定该区域只有一个已知位置的消防站点A,当地图中Q位置发生火灾时(假定有且只有该位置发生火灾),A点接到火警后,立刻出发前往火灾现场。因此,此时的目标为:在满足行车速度时变性的情况下,找到一条用时最少的救援路径。 图4 路网图 为证明不同救援时刻(即路段权重不同)情况下对救援路径选取是有一定影响的,假定选择两个不同时刻从消防站点出发。首先,获取各段道路的权重,根据AHP中获取的路径距离、交通流量、道路等级、天气状况的权重向量与有关数据(假定该交通网中的所有路径均为宽柏油路,天气为晴天)根据式(1)计算得到每一段路径的权重值,图5为A时刻获得的权重值,图6为B时刻获得的权重值。 图5 路段各个道路权重值 图6 路段各个道路权重值 然后,采用融合算法求解最优路径。将上一步计算得到的上述各个路段的权重量引入优化后粒子群蚁群融合算法作为算法中的蚂蚁路径选择时的状态转移概率,得到实时路况下的最优路径。图5情况下得到的最优路径为:A-C-H-L-O-Q;用时9.8 min;权值为47。图6情况下得到的最优路径为:A-C-H-K-Q;用时11.4 min;权值为52。以上结果证明:在不同时刻,由于不同路段的权重不同而导致所选择的救援路径不同,符合实际情况。 本文研究的重点是解决火灾救援时如何在行驶速度时变和各种交通实况下,以时间为优化目标找到一条从消防站点到达火灾现场的最优路径,为此提出了行车速度时变条件下消防灭火救援模型,在融合算法基础上实现了交通实况下火灾救援路径规划,从而保 证了救援路径的时效性。主要研究成果如下:(1)改进了蚁群算法。引入实时动态更新局部信息素与路径优劣排序为依据更新全局信息素相结合的方式替代原有的信息素更新机制;在路径概率选择机制中引入“随机”概率以增加算法的全局搜索能力,并且引入AHP中获得的路径权重结合实时交通速度计算得到的权值作为概率选择的依据;(2)将粒子群算法与优化后的蚁群算法融合。融合算法将PSO得到的次优解作为ACO的初始信息素分布增量,提高了算法的效率和求解精度。 [1] 傅智敏.我国火灾统计数据分析[J].安全与环境学报,2014(6):341-345. [2] 王江波,苟爱萍.火灾中高层住宅小区疏散及救援风险分析[J].消防科学与技术,2015,(01):117-119. [3] 夏劲松. 基于蚁群粒子群算法融合的移动机器人路径规划研究[D].广东:广东工业大学,2012. [4] 雷玉梅.基于改进遗传算法的大规模TSP问题求解方案[J].计算机与现代化,2015(2):34-37. [5] 唐禹.一种路径规划问题的蚁群算法研究[D].哈尔滨:哈尔滨工程大学,2013. [6] Jose B Escario,Juan F Jimenez,Jose M Giron-Sierra.Ant colony extended:experiments on the traveling salesman problem[J].Expert Systems with Applications,2015,42(7):390-410. [7] 李擎,张超,陈鹏.一种基于粒子群参数优化的改进蚁群算法[J].控制与决策,2013(6):873-878,883. [8] 谈晓勇,林鹰.基于混沌蚁群算法的应急救援车辆调度优化[J].计算机应用研究,2014(9):2640-2643. [9] 周东健,张兴国,马海波,等.基于栅格地图-蚁群算法的机器人最优路径规划[J].制造业自动化,2014(5):1-3,10. [10] 张万绪,张向兰,李莹.基于改进粒子群算法的智能机器人路径规划[J].计算机应用,2014(2):510-513. [11] Santos L,Coutinho-Rodrigues J,Current J R.An improved ant colony optimization based algorithm for the capacitated arc routing problem[J].Transportation Research Part B:Methodological,2010,44(2):246-266. [12] 张晨,游晓明.基于栅格模型机器人路径规划的量子蚁群算法[J].电子科技,2016,29(7):1-3,7. [13] 张兴国,周东健,李成浩.基于粒子群-蚁群融合算法的移动机器人路径优化规划[J].江西师范大学学报:自然科学版,2014(3):274-277. [14] 杜博,夏春蕾,戴曙光.融合改进蚁群和粒子群算法的路径搜索应用[J].电子科技,2016,29(9):4-6,135. [15] 叶仕通,万智萍.一种基于改进全局信息素更新效率的蚁群算法及仿真[J].计算机应用与软件,2014(1):176-179. The Particle Swarm Optimization Algorithm Merged with Ant Colony Optimization Algorithm of Fire Rescue Way Research LI Yihong,QIU Jiong (School of Computer Science,Hangzhou Dianzi University,Hangzhou 310018,China) To obtain the optimal relief path, improve the effectiveness of the rescue and the real time,so a particle swarm ant colony fusion algorithm is put forward. The major thinking of the optimization is that on the basis of analyzing the factors influencing the path choice, using the analytic hierarchy process of fuzzy mathematics to evaluate the weight of the road, establish the fire fighting rescue model; Then use the particle swarm algorithm quickly get optimal solution,and take the solution as the initial pheromone increment of ant colony algorithm,put the solved each path weight matrix is introduced into the particle swarm ant colony algorithm to solve the model of state transition probability, then use this improved state transition rules, and consider the traffic speed to obtaine the optimal path of the model.Finally, the experimental results show that this method can accomplish the best relief path planning. particle swarm optimization; ant colony optimization; fusion algorithm; optimize ;the relief path 2017- 03- 01 浙江省科技计划项目(GK090910001) 李怡弘(1991-),女,硕士研究生。研究方向:消防物联。裘炅(1973-),男,博士,副教授。研究方向:消防物联。 TP311.5 A 1007-7820(2018)01-058-05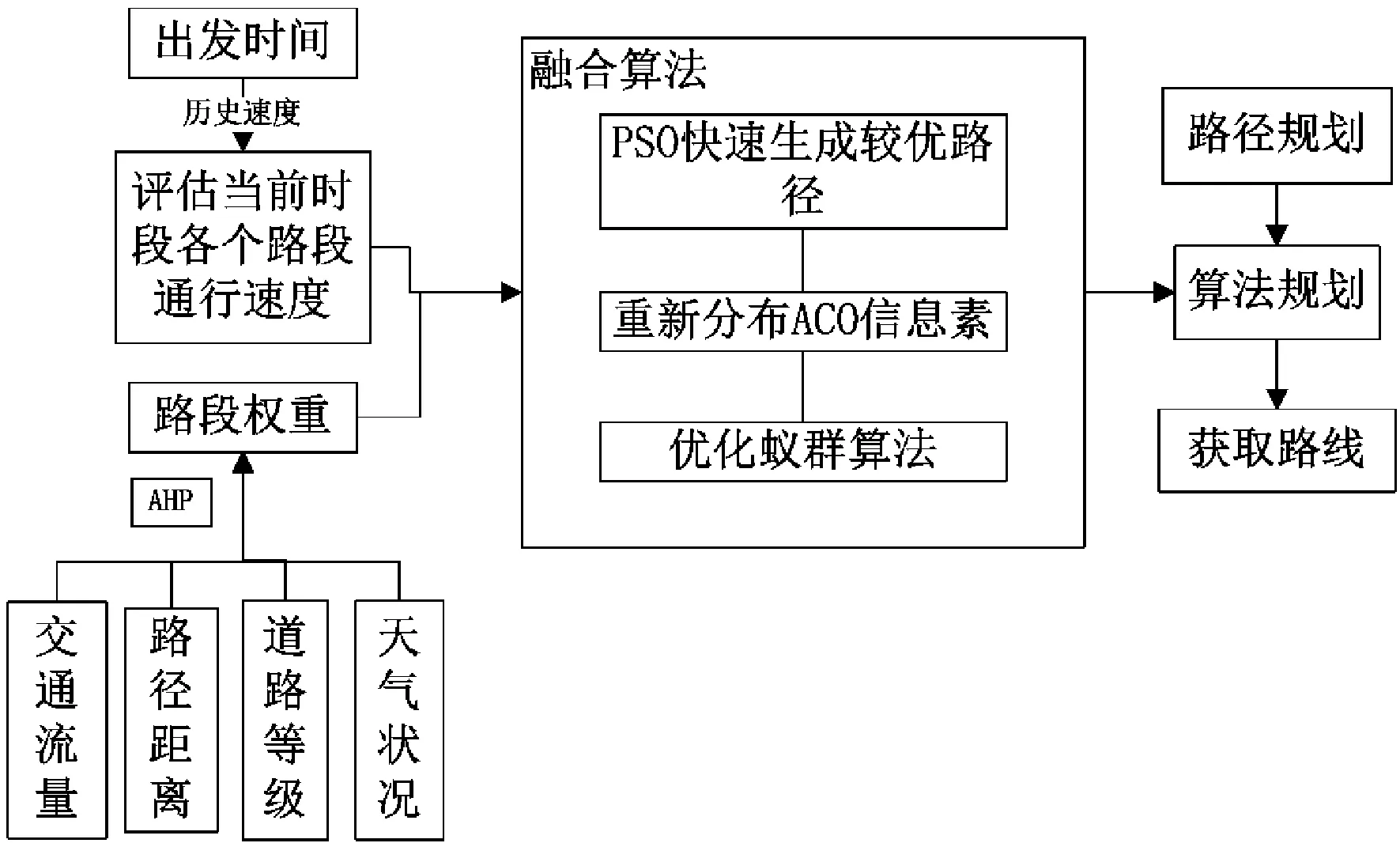
2 相关算法概述
2.1 粒子群优化算法基本原理
2.2 蚁群算法基本原理及优化
3 改进的粒子群蚁群融合算法实现
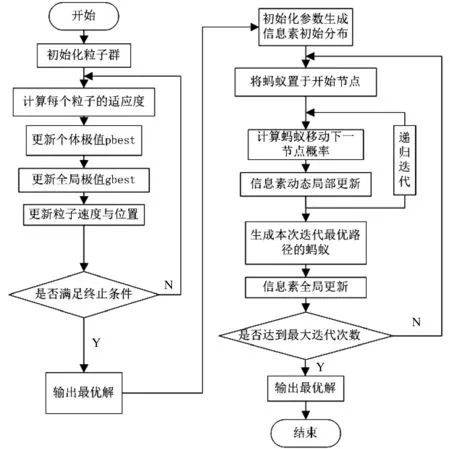
4 仿真结果

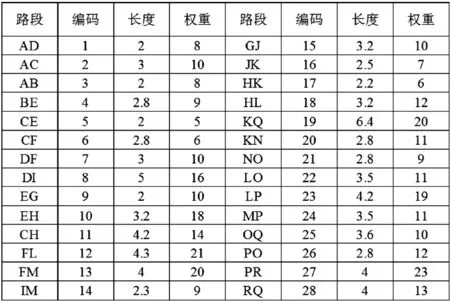
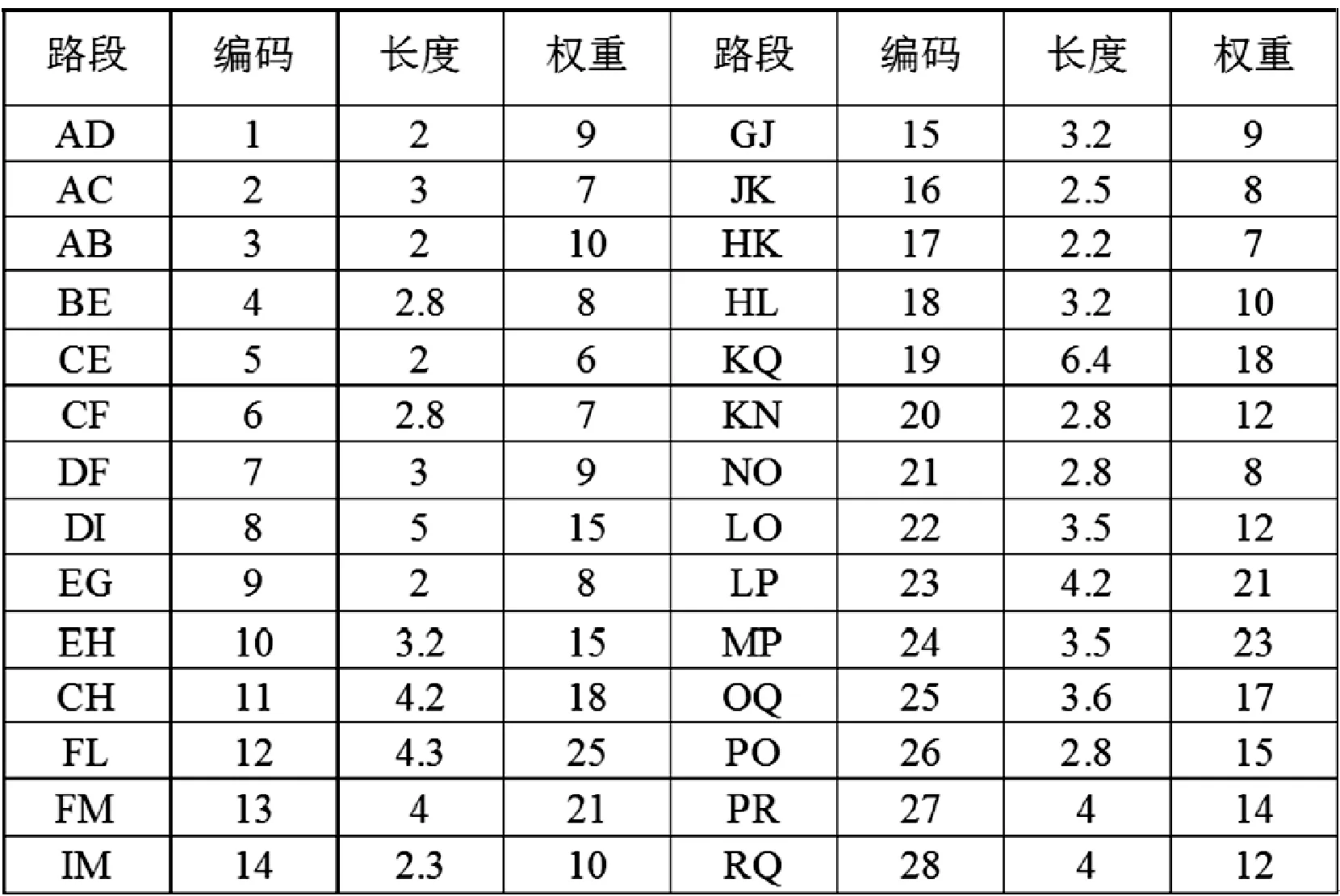
5 结束语

