并行人工蜂群算法研究
梅 凯,火久元,常扣扣
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
并行人工蜂群算法研究
梅 凯,火久元,常扣扣
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
针对人工蜂群算法在处理高维度问题时收敛速度慢的问题,利用OpenMP多线程技术和规约机制,并根据已改进的观察蜂来选择雇佣蜂的方式,提出了基于OpenMP的并行人工蜂群算法(PCABC)。仿真实验分别在问题维度为100和200下进行来评估算法性能,在4个逻辑处理器环境下,基于静态调度的并行人工蜂群算法的加速比最高可以达到3.95,效率可达98.65%。实验结果表明,PCABC并行人工蜂群算法在处理高维度复杂函数时,收敛速度和算法运行时间都有较大的提升。
人工蜂群算法;人工蜂群算法改进;群体智能;并行化;OpenMP并行处理
人工蜂群算法[1]是一种新兴的群智能优化算法,由土耳其学者Karaboga在2005年提出,它具有设置参数少、易于实现、计算简单等优点,特别适合工程应用[2]。文献[3]将人工蜂群算法与其他其它群智能算法(遗传算法[4]、粒子群算法[5]等)进行了比较,证明人工蜂群算法的性能要接近甚至优于其他算法。文献[6]将人工蜂群算法进行了改进并应用到语音识别模型中,识别结果显示了人工蜂群算法及其改进的人工蜂群算法具有良好的性能。文献[7]通过引入基于引导素的化学通信方式,提出了一种基于引导素更新和扩散机制的人工蜂群算法,并将改进后的算法应用在0-1多维背包问题上。文献[8]将人工蜂群算法做了改进并应用到人工神经网络中,优化了网络的均方误差函数。但是标准的人工蜂群算法在解决高维函数优化时,收敛速度较慢,算法运行时间较长。为此,本文经过深入研究,并结合文献[9]中已改进的观察蜂来选择雇佣蜂的方式,提出了并行人工蜂群算法(PCABC)算法,很好地解决了这一问题。
1 人工蜂群算法原理
在人工蜂群算法中,蜜源被抽象成待优化问题的解,蜜源的收益率(蜜源浓度、离蜂巢的距离等)越好,表示解的质量越好。蜜蜂被分为3种类型:雇佣蜂、观察蜂和侦查蜂。进化迭代主要由这3种蜜蜂完成:(1)雇佣蜂在其记忆的花蜜源附近进行局部随机搜索,同时将蜜源信息传递给观察蜂;(2)观察蜂从中选择较优的蜜源,然后在这些蜜源周围做进一步的搜索;(3)侦察蜂对长期得不到更新的蜜源进行更新。
ABC算法的具体步骤如下:
(1)算法初始化:算法在给定的取值范围内按照式(1)随机产生n个食物源信息
xij=r·(maxj-minj)+minj
(1)
式中,r为(0,1)之间的随机数,maxj和minj为第j维取值的上限和下限;
(2)计算每个食物源的适应度值;
(3)雇佣蜂更新食物源:雇佣蜂在食物源附近按照式(2)搜索新蜜源,比较新旧食物源的优劣,若新食物源优于旧食物源,则用新的食物源信息覆盖旧食物源信息,否则保留旧的食物源,局部寻优次数加1
(2)
其中i≠j,r为[-1,1]之间的随机数;
(4)观察蜂更新食物源:观察蜂根据雇佣蜂的舞蹈信息,按照轮盘赌方式选择食物源,并在其附近按式(2)搜索新蜜源。并根据贪婪选择的方式确定保留的蜜源。若蜜源没有被更新,则局部寻优次数加1。观察蜂选择蜜源的概率按照式(3)进行计算
(3)
(5)侦察蜂更新食物源:抛弃停滞次数达到 的食物源,并按照式(1)在给定的取值范围内随机生成新的食物源;参数 的作用是使长期得不到更新的引领蜂获取重生[10];
(6)达到最大循环次数:判断算法是否达到算法预定的最大循环次数MaxCycle,是则算法结束,否则转步骤(3)进行下一次迭代。
2 并行人工蜂群算法
2.1 人工蜂群算法并行性分析
群体智能算法是基于种群行为对给定的目标进行寻优的启发式搜索方法,其寻优过程体现了随机、并行和分布式等特点[11],所以群体智能算法适合做并行化计算。人工蜂群算法作为一种群体智能算法,具有天然的并行性。可以设想,在真正的大自然中,所有的蜜蜂进行花蜜源搜索的时候,都是各自完成各自范围的搜索任务,独立地把花蜜源的信息带到蜂巢,这是明显的并行性特征。同样,当蜜蜂将自己的信息带回蜂巢进行信息共享的时候,其他的蜜蜂也没有因此而停止对各自蜜源的搜索,这也是天然并行性的体现[12]。可以认为根据蜂群采蜜行为设计的人工蜂群算法也有并行性。图1所示为蜜蜂采蜜过程的示意图。
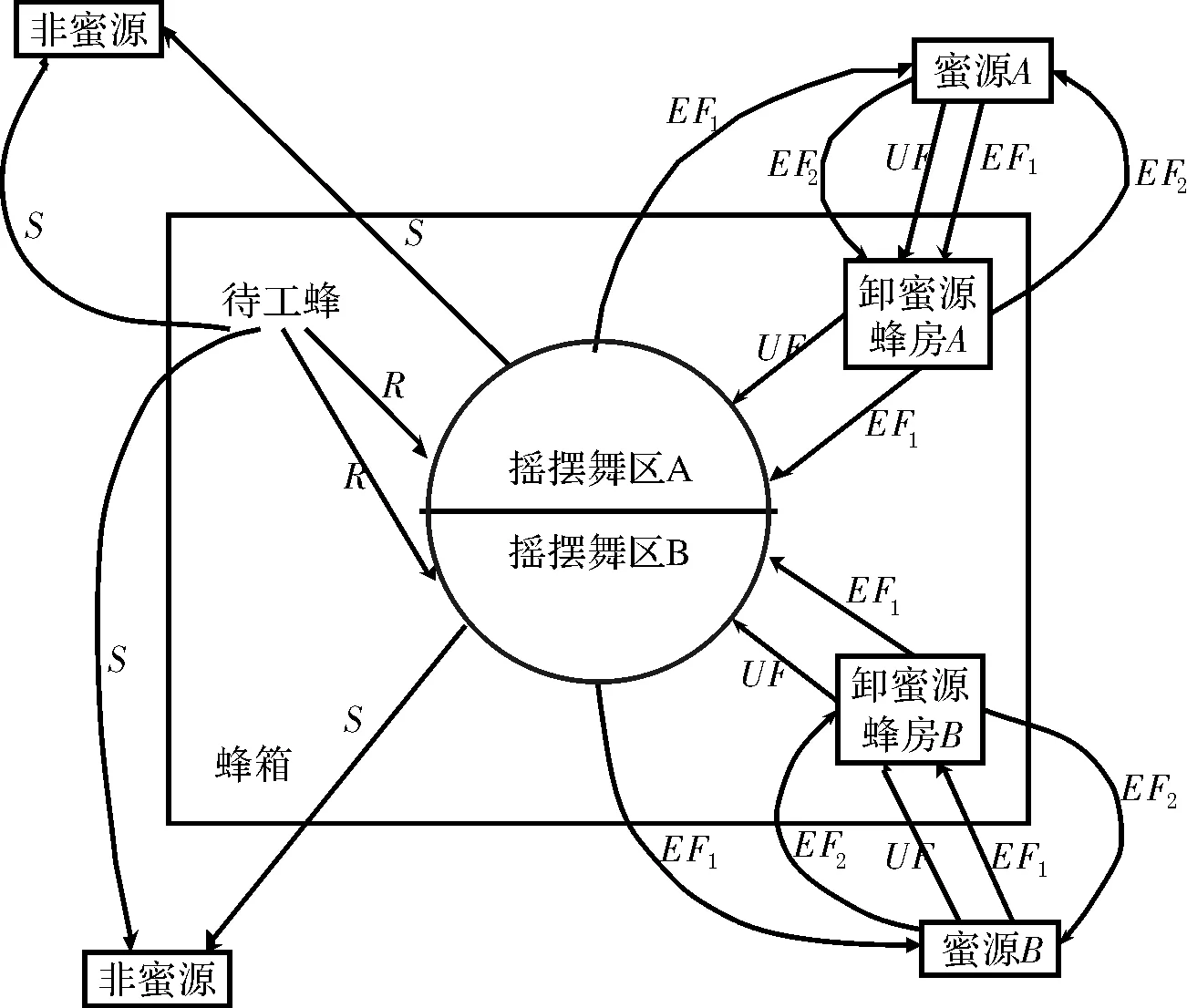
图1 蜜蜂采蜜过程
2.2 OpenMP
按存储方式对并行计算机进行分类[13],并行计算机可以简单分为共享式内存和分布式内存。共享内存就是多个核心共享一个内存,一般的大型计算机结合分布式内存和共享内存结构,在每个计算节点内是共享内存,节点间是分布式内存,如图2所示。
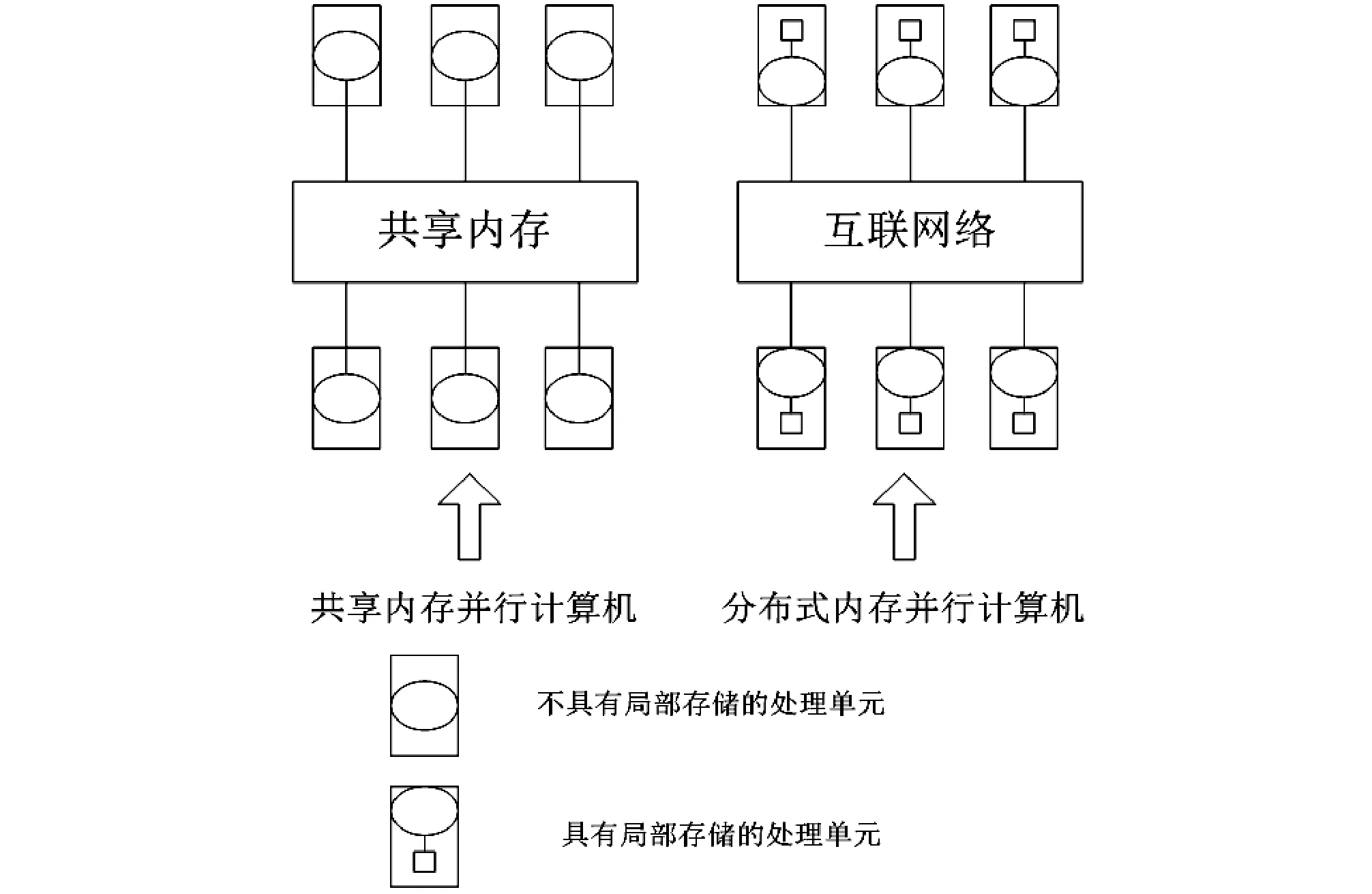
图2 按存储方式对并行计算机进行分类
OpenMP(Open Multi-Processing)是一种基于共享内存编程模型的并行化技术,它基于编译制导,具有简单、移植性好、可扩展性高以及支持增量并行化开发等优点,已经成为共享存储系统中的并行编程标准。
1.2.6 疼痛护理:对于患者术后出现疼痛的情况,若患者属于轻度疼痛,嘱患者使用呼吸方法进行肢体放松的训练:呼吸时深而慢,呼吸频次控制在10次/min,每次进行15 min左右的锻炼。或应用音乐疗法,嘱患者听轻快舒缓的音乐,以患者术后疼痛。若患者疼痛剧烈,根据实际情况,遵医嘱按时使用镇痛药物。
OpenMP有3大组成要素:环境变量、编译制导指令、API函数。实验中,主要设置两个环境变量的值:OMP_NUM_THREADS和OMP_SCHEDULE。OMP_NUM_THREADS环境变量用于设置并行域中的线程个数,本文将其设为omp_get_num_procs()函数的返回值。omp_get_num_procs()函数的作用是返回系统中处理器的个数。本文所做实验中,omp_get_num_procs()函数的返回值为4。在OpenMP中,OMP_SCHEDULE环境变量对应3种循环并行化调度类型:静态调度、动态调度和指导调度[14],size参数为3种调度类型的可选参数。
2.3 并行人工蜂群算法具体实现
实验考虑到OpenMP特性和实验环境,采用不改变蜂群算法基本结构,保持只有一个种群的主从式并行模型,耗时多的计算适应度函数部分[15-16]采用多线程并行执行。
本文设计的并行人工蜂群算法(PCABC)的流程图如图4所示,主要包括以下步骤:
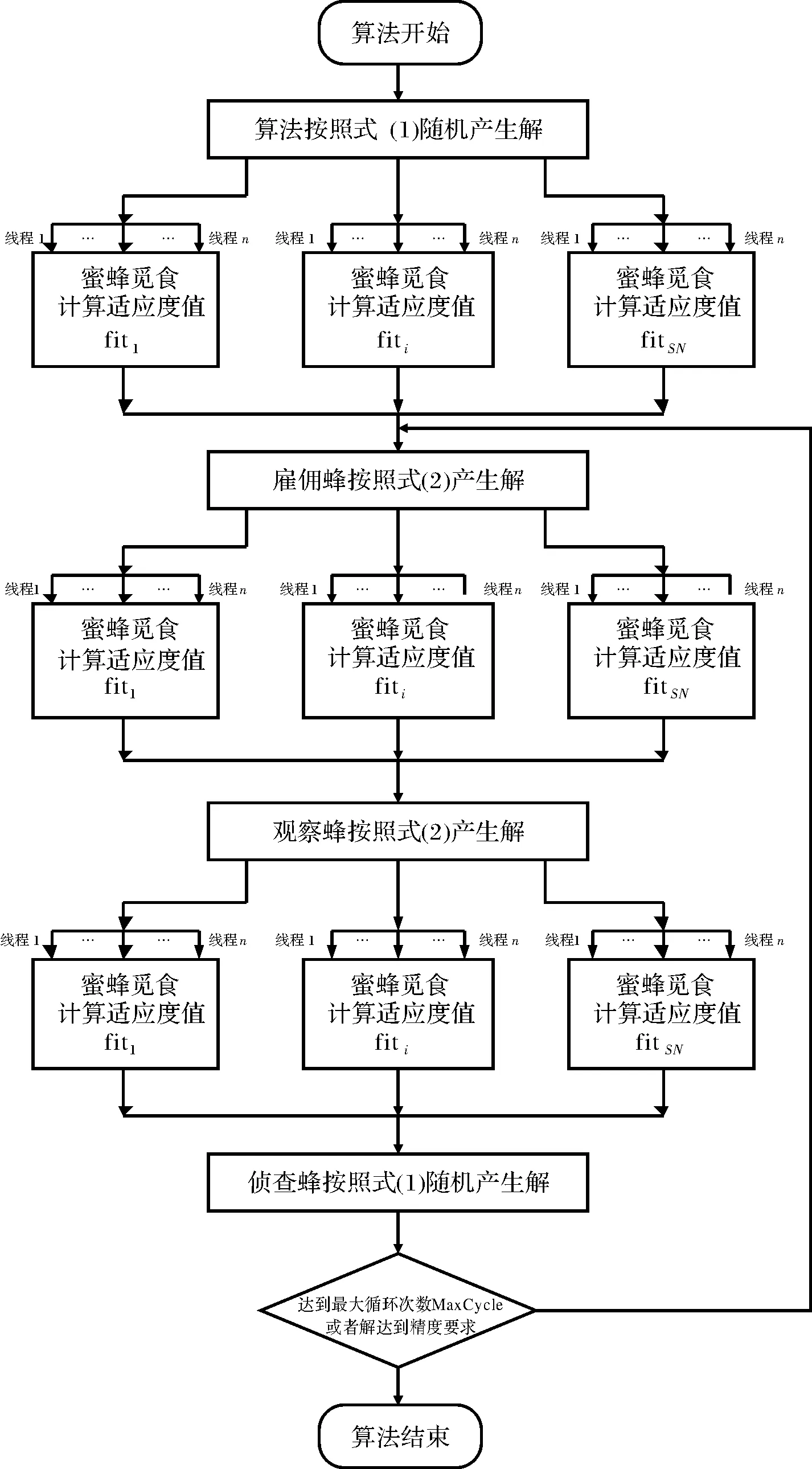
图3 并行人工蜂群算法示意图
(1)算法初始化:主线程完成算法的初始化,初始化食物源个数FN,最大迭代次数MaxCycle,最大局部探优次数Limit,优化空间维度D,在给定的取值范围内按照式(1)随机产生FN个食物源信息;
(2)计算每个食物源的适应度值:算法进入并行区,并行计算每个食物源的适应度值,本文采用4个线程并行计算,并使用OpenMP规约机制[14]对并行结果进行汇总,计算完成后,算法退出并行,回到主线程继续执行步骤(3);
(4)观察蜂更新食物源[9]:观察蜂根据雇佣蜂跳的“摇摆舞”信息,按照轮盘赌方式选择食物源,并在其附近按式(4)搜索新蜜源。算法进入并行区,并行计算新蜜源的适应度值,并使用OpenMP规约机制对并行结果进行汇总,计算完成后,算法退出并行,回到主线程中,根据贪婪选择方法确定保留的食物源
(4)
(5)侦查蜂更新食物源:主线程抛弃停滞次数达到Limit的食物源信息,并按照式(1)在给定的取值范围内随机生成新的食物源;
(6)达到最大循环次数:主线程判断算法是否达到预定的最大循环次数MaxCycle,是则算法结束,否则转步骤(3)进行下一次迭代。
3 实验及结果分析
3.1 实验平台及参数
实验在Inter(R) Core(TM) i3CPU M 370、主频2.4 GHz,内存4 GB,4个逻辑处理器的个人电脑上进行,操作系统是Windows 10,基于Visual Studio 2010编程工具,C++语言实现,采用OpenMP多线程并行编程技术。本文将已改进的观察蜂来选择雇佣蜂的人工蜂群算法记为CABC,标准人工蜂群算法的并行化算法记为PABC,将并行的CABC算法记为PCABC。
仿真实验中,蜜蜂种群大小SN=80,食物源个数FN=SN/2,问题维数分别取D=100和D=200,最大循环次数MaxCycle=10 000,最大局部寻优次数Limit取值按公式0.25×NP×D[17]计算,算法独立运行30次,选取OpenMP静态调度进行实验。本文的所有实验均在没有设置size参数的条件下进行。实验选取4个基准函数进行对比测试。
(1)f1:Sphere函数
Sphere函数是连续的单峰函数,各分量在xi=0(i=1,2,…,n)时达到最小值0[12];
(2)f2:Rosenbrock函数
Rosenbrock属于一种单峰函数里比较复杂的病态函数,其全局最优点位于一个平滑、狭长的抛物线型山谷内,搜索的过程中比较难辨别方向,也极难找到全局最小点,通常用来评价算法的执行效率[9]。Rosenbrock函数在xi=1(i=1,2,…,n)时达到最小值0。
(3)f3:Rastrigin函数
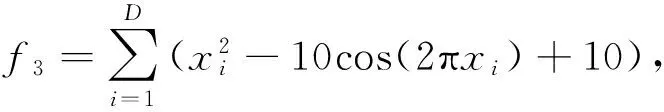
Rastrigin函数为多峰函数,在定义域范围内大约存在10n(n为问题的维数)个局部极小点,是典型的非线性多模态函数,峰形呈高低起伏不定跳跃性的出现,所以一般的优化算法很难搜索到全局最优值[9]。Rastrigin函数在xi=0(i=1,2,…,n)时达到最小值0。
(4)f4:Griewank函数
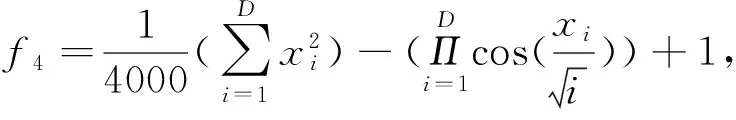
Griewank函数也为典型的非线性多模态函数,含有大量的局部极值点,数目与问题的维度有关,随着函数维度的增加,极值点的个数会成指数倍数增长,整个
函数具有广阔的搜索空间。所以Griewank函数通常被认为是一般的优化算法比较难处理的复杂多模态优化问题[9]。Griewank函数在xi=0(i=1,2,…,n)时达到最小值0。
在处理Griewank函数时,考虑到Griewank是在Sphere函数的基础之上增加了cos函数,之后的实验结果证明了在D=100维和D=200维时,Sphere函数的并行效果并不好,所以在这里本文只对Griewank函数的后半部分做了并行的规约操作。
3.2 实验结果及分析
D=100维下的并行化实验结果如表1所示,实验设置的参数为:蜜蜂种群数量SN=80,食物源数量FN=SN/2=40,问题维度D=100,最大循环次数MaxCycle=10 000,最大局部寻优次数Limit=0.25×NP×D[17]=2 000,算法独立运行30次。
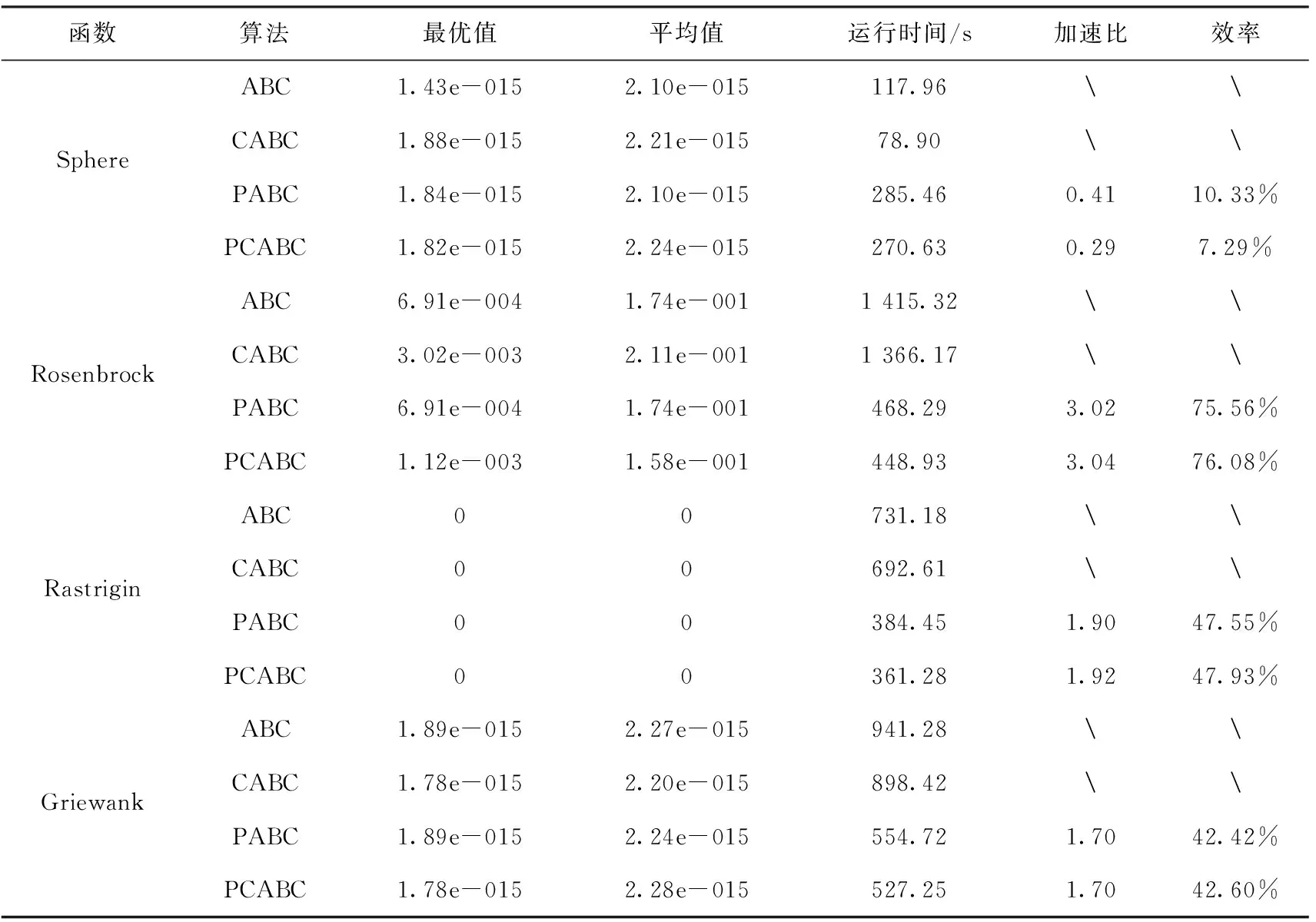
表1 D=100维下的并行化实验结果
D=200维下的并行化实验结果如表2所示,实验设置的参数为:蜜蜂种群数量SN=80,食物源数量FN=SN/2=40,问题维度D=200,最大循环次数MaxCycle=10 000,最大局部寻优次数Limit=0.25×NP×D[17]=4 000,算法独立运行30次。
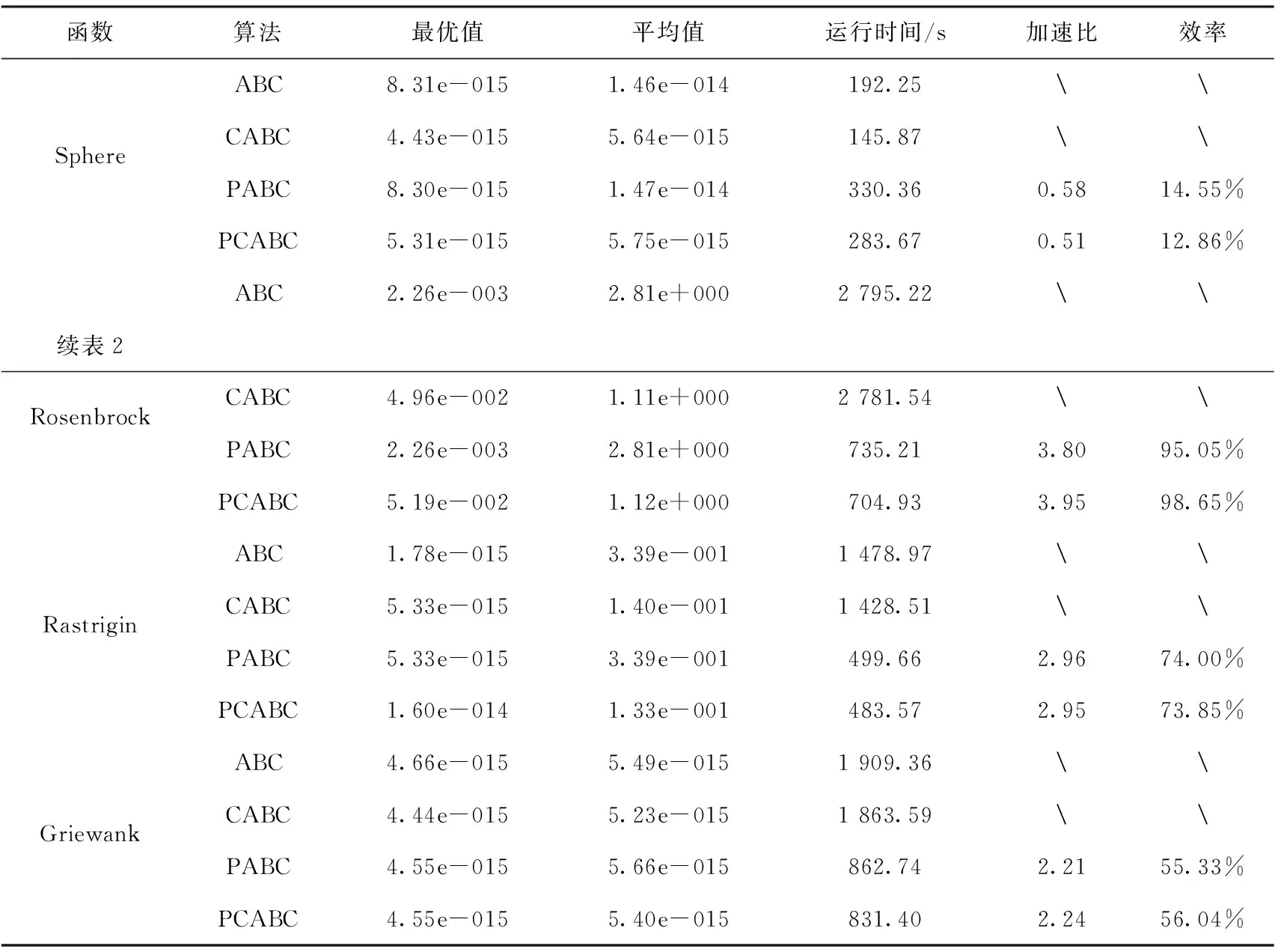
表2 D=200维下的并行化实验结果
3.3 结果分析
分析1通过表1和表2的实验数据,不难发现,除了相对简单的Sphere函数,在D=100维和D=200维时,PABC算法和PCABC算法均比ABC算法和CABC算法的运行时间少,对于简单的Sphere函数,并行时间反而比串行时间长,这是因为并行运算有创建线程、同步线程和销毁线程的时间,当计算量比较少时,这部分的时间就变为主要的消耗时间。
分析2通过对比表1和表2的数据,可以发现,随着维度的增加,算法的运行时间越长,加速比和效率越大,且加速比向4靠近(在本文所做实验中,逻辑处理个的个数是4),但是都小于4。PCABC算法对Sphere函数的优化精度略有提高,但是收敛时间较标准人工蜂群算法长,PCABC算法对Rosenbrock函数和Rastrign函数的优化精度略低于标准人工蜂群算法,但是算法运行时间远远少于标准人工蜂群算法,这说明PCABC算法对Rosenbrock函数和Rastrign函数在优化精度和优化时间上达到了权衡,PCABC算法对Griewank函数的优化精度和优化时间均优于标准人工蜂群算法。
分析3对比表1和表2可以发现,问题的维度越大,算法收敛的时间越长。并行PABC算法和PCABC算法总体收敛速度要优于串行ABC算法和CABC算法,这是因为,PABC算法和PCABC算法采用了OpenMP并行机制,在相同的时间内,可以做更多的运算工作。PCABC算法的收敛速度要稍优于PABC算法,CABC算法的收敛速度要稍优于ABC算法,这是因为CABC算法和PCABC算法能够保证当前获得的最优解引导种群进化,使算法逐渐收敛到全局最优解。
4 结束语
针对人工蜂群算法在处理高维复杂问题时收敛速度慢的问题,本文提出的基于OpenMP的采用主从并行模型的并行人工蜂群算法PCABC能够以较快的速度收敛。实验结果证明,在高维度复杂函数的情况下,PCABC算法相对于标准人工蜂群算法在运行时间和收敛速度上都有较大的提升,这是因为PCABC算法对耗时多的计算适应度函数的部分做了并行处理,大幅提升了算法的运行时间和收敛速度,同时PCABC算法利用式(4),保证算法当前获得的最优解引导种群进化,进一步加速了算法的运行时间和收敛速度。本文对人工蜂群算法的研究方法同样适用于研究其他群智能算法。下一步工作将是分析并行人工蜂群算法size参数和其他并行化调度类型对并行人工蜂群算法收敛的影响。
[1] Karaboga D.An idea based on honey bee swarm for numerical optimization[M]. Erciyes:Erciyes University,2005.
[2] 毕晓君,王艳娇.加速收敛的人工蜂群算法[J].系统工程与电子技术,2011(12):2755-2761.
[3] Karaboga D,Akay B.A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation,2009,214(1):108-132.
[4] Holland J H.Adaptation in natural and artificial systems[M].Ann Arbor, MI:University of Michigan Press,1975.
[5] Kennedy J, Eberhart R.C.Particle swarm optimization[C].MI,USA:1995 IEEE International Conference on Neural Networks,1995.
[6] 宁爱平.人工蜂群算法及其在语音识别中的应用研究[D].太原:太原理工大学,2013.
[7] 魏红凯.人工蜂群算法及其应用研究[D].北京:北京工业大学,2012.
[8] 王允霞.蜂群算法的研究及其在人工神经网络中的应用[D].广州:华南理工大学,2013.
[9] 何鹏.人工蜂群算法研究[D].上海:华东理工大学,2014.
[10] 袁亚杰.一种改进的人工蜂群算法[J].中国科技信息,2011(24):102-103.
[11] 刘丽丽.基于智能算法的网络入侵检测技术研究[D].南京:江南大学,2009.
[12] 江铭炎,袁东风.人工蜂群算法及其应用[M].北京:科学出版社,2014.
[13] 都志辉.高性能计算并行编程技术[M].北京:清华大学出版社,2001.
[14] 罗秋明,明仲.OpenMP编译原理及实现技术[M].北京:清华大学出版社,2012.
[15] Parpinelli R S,Beritez C M V,Lopes H S.Parallel approaches for the artificial bee colony algorithm[M].UK:Swarm Intelligence,2011.
[16] 徐昆.群智能算法及其并行计算技术的研究与应用[D].济南:山东大学,2014.
[17] M Subotic,M Tuba,N Stanarevic.Parallelization of the Artificial Bee Colony (ABC) algorithm[C].Weston DC:Wseas International Conference on Nural Networks &Wseas International Conference on Evolutionary Computing &Wseas International Conference on Fuzzy Systems,2010.
A Parallel Approach for Artificial Bee Colony Algorithm
MEI Kai,HUO Jiuyuan,CHANG Koukou
(School of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
Aiming at the slow convergence speed of artificial bee colony algorithm in dealing with high dimensional problems, this paper uses OpenMP multi-threading technology and regulation mechanism, and according to the improved way onlooker bees choose employed bees, a parallel artificial bee colony algorithm(PCABC) based on OpenMP is proposed. Simulation experiments are performed to evaluate the performance of the algorithm under three different types of cyclic parallel scheduling types of OpenMP. In the 4 core processor environment, the speedup of parallel artificial bee colony algorithm based on static scheduling can reach to 3.95, the efficiency can reach to 98.65%.The experimental results show that the PCABC parallel artificial bee colony algorithm has higher lifting speed and running time when dealing with high dimensional complex functions.
artificial bee colony algorithm;improved artificial bee colony algorithm;swarm intelligence;parallelism; OpenMP parallel processing
2017- 03- 14
国家自然科学基金(61462058);甘肃省自然科学研究基金计划(1606RJZA004);2016年赛尔网络下一代互联网技术创新项目(NGII20160111)
梅凯(1989-),男,硕士研究生。研究方向:智能计算、并行计算等。火久元(1978-),男,博士,副教授。研究方向:智能计算、并行计算、数据挖掘等。
TP31
A
1007-7820(2018)01-020-06

