水位下降对平山水库黏土心墙坝渗流场和稳定性影响分析

(吉安市水利水电规划设计院， 江西 吉安 343000)

水位下降对平山水库黏土心墙坝渗流场和稳定性影响分析

胡淑娟

(吉安市水利水电规划设计院， 江西 吉安 343000)

本文以平山水库黏土心墙坝为例，计算得到了库水位从校核洪水位下降至正常蓄水位和死水位，坝体内部浸润线分布和上下游坝坡的最小安全系数。结果表明：随着库水位下降，浸润线也逐渐降低，心墙内浸润线由直线变为折线；校核洪水位时最大渗流速度可达0.4503m/d；上下游坝坡的最小安全系数随水位降低而减小，但均满足规范要求；水位下降导致心墙与上游坝体交界处的剪应变范围增大，并有向上游坝坡扩展的趋势。

土石坝；心墙；浸润线；渗流；变应变

1 工程概况简介

平山水库位于县城西南3km处的平山河中游，河流全长约28km，流域面积为556km2，控制流域面积431km2。水库大坝校核洪水位高程116m，正常蓄水位112.6m，死水位103.8m，总库容约2亿m3，水库有效库容1.15亿m3，库容系数为0.575，属于大(二)型水库，主要建筑物为2级，次要建筑物为3级，临时性建筑物级别为4级。

大坝坝顶高程为2825.2m，最大坝高为75.2m，属高坝，坝顶宽度为10m。根据规范规定与实际结合，上游坝坡上部取2.5，下部取3.0，下游自上而下均取2.5，下游在2800m、2775m高程处各变坡一次。在坝坡改变处，尤其在下游坡，设置2m宽的马道(戗道)汇集坝面的雨水，防止冲刷坝坡，并同时兼作交通、观测、检修之用。枢纽建筑物平面布置见图1。

筑坝土料主要有黏土、壤土和少量坡土，其各项性能参数见表1。

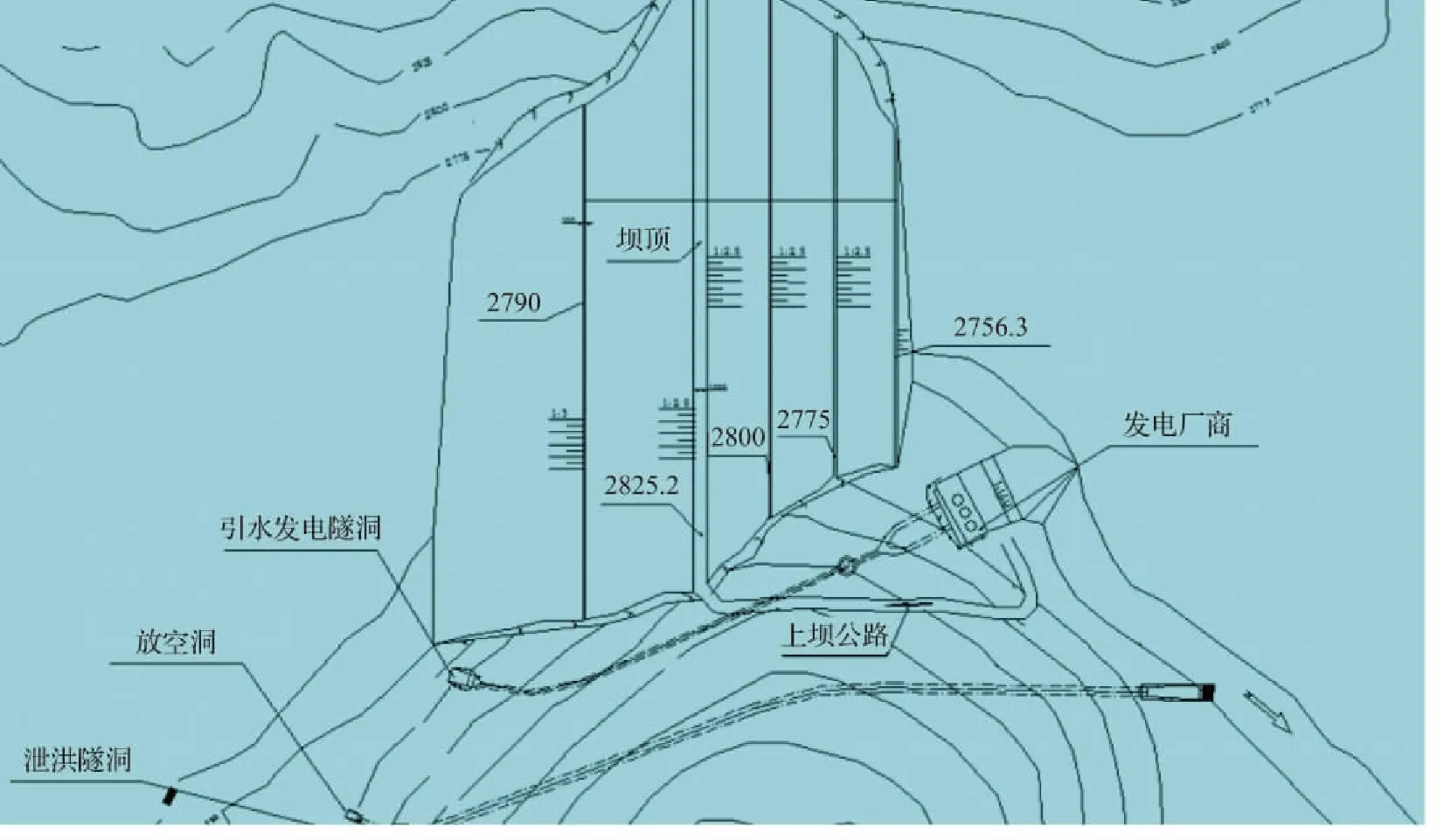
图1 枢纽建筑物平面布置

筑坝材料浮容重γ′/(KN/m3)湿容重γ/(KN/m3)土粒比重GS干容重γd/(KN/m3)孔隙率n/(%)内摩擦角/φ粘聚力c/(kPa)渗透系数K/(cm/s)黏土13191262163019°401×10-7壤土141782601583222°141×10-5坡土1518627316639828°751×10-3

由于当地雨量分布极为不均，干旱和洪涝灾害时有发生，水库大坝常处于水位骤变的运行工况，对坝体的稳定性产生很大影响。为此，本文基于坝体渗流和稳定基本理论，对土石坝在不同水位下的浸润线和稳定性进行定量分析，计算结果可为水库的调控提供依据，保障大坝和下游的安全。

2 渗流计算原理

2.1 渗流基本理论

土是一种三相多孔介质，其孔隙在空间上相通。在饱和土中，水充满整个孔隙，当土中不同位置存在水位差时，土中水就会在水位能量作用下，从水位高(即能量高)的位置向水位低(即能量低)的位置流动。则液体(如土中水)从物质微孔(如土体孔隙)中透过的现象称为渗透，流体在孔隙介质中的流动即为渗流。由于渗流骨架的岩土性质与其中流体的性质较为复杂，所以常用平均概念和综合性的参数代表其渗流性质。[1-3]

a.渗流基本定律——达西定律

最早，法国工程师达西(H.Darcy)[4-5]在垂直圆管中装砂进行渗透试验，试验结果证明，渗透量Q除与断面面积A直接成正比外，正比于水头损失hw，反比于渗径长度L，引入决定土粒结构和流体性质的一个常数k，则

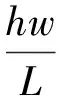
(1)

式中k——反映土的透水性质的比例系数，称为渗透系数。

达西渗透定律为：

(2)

上式表明在均质孔隙介质中渗流流速与水力梯度的一次方成比例并与土的性质有关。但是，达西渗透定律仅在一定范围内才能使用，即流体做层流运动时方可，在水利工程中，除了堆石坝、堆石排水体等大孔隙介质中的渗流为湍流之外，绝大多数渗流均属于层流范围。

b.二维渗流的连续性方程

当渗流场中水头及流速等渗流要素不随时间改变时，这种渗流为稳定渗流。对稳定渗流场中任意点A处的以微小单元，面积为dxdz，厚度为dy=1，在x和z方向各有流速vx和vz。单位时间内流入这个微小单元体的渗流量为dqe，则

dqe=vxdz×1+vzdx×1

(3)

单位时间内流出这个微小单元体的渗水量为dq0，则

(4)

假定水体不可压缩，则根据水流连续原理，单位时间内流入和流出微小单元体的水量应该相等，即

dqe=dq0

(5)

由上得到二维渗流连续方程：

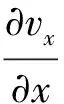
(6)

c.二维渗流的基本微分方程

假设液体和固体骨架都不可压缩，于是，可得到不可压缩介质中的渗流基本微分方程，也称为稳定渗流微分方程：根据达西渗透定律，对于各向异性土：

(7)

(8)

式中kxkz——表示x和z方向的渗透系数；

h——测管水头。

由上述可得：在二维平面渗流的情况下，均匀各向异性土体的渗流基本微分方程为:

(9)

对于各向同性的均质土，kx=kz，则可得到著名的拉普拉斯方程，也是平面稳定渗流的基本微分方程：

(10)

d.渗流有限元分析的基本方法

有限元法是数值计算方法中应用最广的一种，其基本方法是将连续的求解区域离散化为一组有限的、且按一定方式相互连接在一起的单元组合体，利用每一个单元内假设的近似函数来分片地表达整个求解域上待求的未知场函数。并通过插值函数计算出各个单元内场函数的近似值，进而得到整个求解域上场函数的近似值。显然，随着单元数目的增加，或单元自由度的增加及插值函数精度的提高，解的近似程度将不断改进，只要计算满足设置的收敛要求，近似解将最终收敛于精确解。

2.2 稳定基本理论

稳定分析是确定大坝剖面安全的主要依据，对大坝的经济性和安全性具有重要影响。摩尔—库仑理论是目前应用最为广泛的屈服准则，在工程上采用的土坡稳定分析方法，主要是建立在极限平衡理论基础上，假设达到极限平衡状态时，土体将沿某一滑裂面产生剪切破坏而失稳，滑裂面上各点，土体均处于极限平衡状态，满足摩尔—库仑强度条件。[6～8]

Fenenius根据在瑞典岸边发生的圆弧滑动破坏，首次提出了瑞典条分法基本概念。除了假定滑裂面是个圆柱面外，还假定不考虑土条两侧的作用力，安全系数定义为每一土条在滑裂面上所提供的抗滑力矩之和与外荷载及滑动土体在滑裂面上所产生的滑动力矩和之比。瑞典法的推导通常采用总应力法，同样可用有效应力法(考虑孔隙水压力)计算并按定义的安全系来推导公式。为了考虑条间力的作用，可假定每一土条两侧作用力的合力方向均和该土条底面平行，因此在进行土条底部法线方向力的平衡时，可以不予考虑。安全系数计算公式：

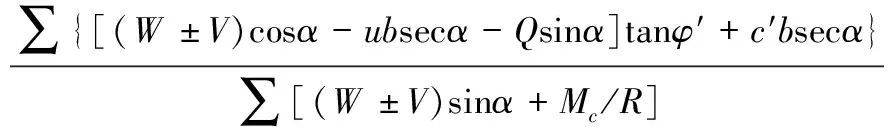
(11)

式中W——土条重量；

Q、V——分别表示水平和垂直地震惯性力(向上为正，向下为负)；

u——作用土条底面的孔隙压力；

α——条块重力线与通过此条块底面中点的半径之间的夹角；

b——土条宽度；

c′、φ′——土条底面的有效应力抗剪强度指标；

Mc——水平地震惯性力对圆心的力矩；

R——圆弧半径。

3 计算结果及分析

3.1 渗流分析

土石坝的渗流计算主要是确定坝体的浸润线的位置，为坝体的稳定分析和布置观测设备提供依据，以便选取适合的控制措施。对河床中间典型断面进行渗流计算，计算主要针对校核洪水位、正常蓄水位及死水位的工况进行，计算模型如图2所示。

通过对不同特征水位下心墙坝进行稳定渗流计算，得到了校核洪水位、正常蓄水位和死水位下土石坝坝体内的浸润线分布，如图3所示。分析可以发现：在校核洪水位时，位于心墙内的浸润线近乎为直线，心墙右侧浸润线水平分布；当水位下降至正常蓄水位时，上游水平面与心墙相隔有一定距离，坝体内浸润线变化不大；而当水位下降至死水位时，上游水平面与心墙之间的距离大大增加，心墙上游和下游的浸润线均与两侧水平面相接，呈水平分布，而心墙内浸润线表现为折线，连接上游段较缓，连接下游段斜率更大，说明设置的心墙能有效降低浸润线的高度，提高了坝体的抗渗性能。

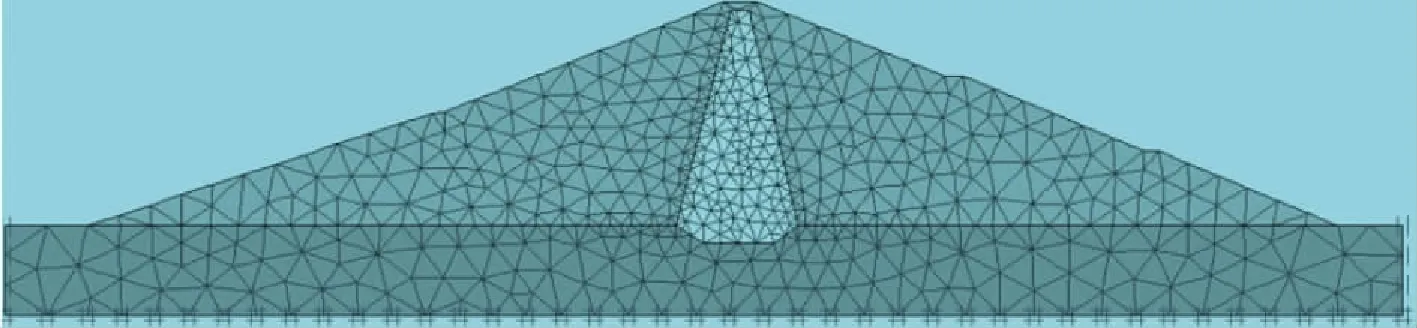
图2 心墙坝网格模型及边界条件设置

图3 不同特征水位坝体浸润线分布

此外，根据土石坝渗流计算结果，统计得到了3种不同特征水位下下游溢出点高程和最大的渗流速度，计算结果见表2。分析可见，随着水位的降低，下游溢出点高程也随之下降，而最大的渗流速度在校核洪水位工况时最大，为0.4503m/d，在正常蓄水位时最大渗流速度减小至0.2647m/d，库水位降低至死水位时最大渗流速度为0.2866m/d。3种水位下出现最大渗流速度的位置均位于浸润线出口部位，如图4为正常蓄水位时渗流速度分布，可见渗流主要发生在浸润线出口。

表2 大坝渗流计算成果

注坝基高程2750m

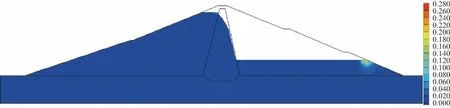
图4 正常蓄水位时渗流速度分布(m/day)

3.2 稳定性分析

心墙坝的上下游坝坡滑动时形成折线滑动面，根据有效应力原理，土体的有效应力等于总应力与孔隙水压力的差值，所以部分浸水的非黏土坝坡，由于水位上下的土料容重不同，有水时内摩擦角φ和黏聚力c值也有所降低，此时坝坡失稳时最可能的滑动面近乎折线。[9-10]在滑动面上抗剪强度的发挥是一样的，安全系数的表示方式为：

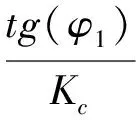
(11)

式中φ1、φ2、φ3——实验得到的抗剪强度指标，由c和φ确定。

分别采用极限平衡法(瑞典条分法)和强度折减法定量计算了不同特征水位下，上下游坝坡的最小安全系数，稳定计算成果见表3。

根据计算成果表可看出：采用极限平衡法和强度折减法计算的最小安全系数Kmin均满足规范值要求[11]，其中极限平衡法计算的Kmin值稍小，偏于安全，但相差不超过0.02，下文分析以极限平衡法为准。

表3 大坝上下游坝坡稳定计算成果

由于上游坝坡较缓，在校核洪水位时，最小安全系数Kmin=1.40，随着水位下降，Kmin值也逐渐减小，在死水位时仅有1.33，但大于规范规定值1.25。下游坡情况类似，Kmin值也随水位的降低而逐渐减小，在校核洪水位时Kmin=1.49，在死水位时为1.42，下游坡的最小安全系数均大于相同工况的上游坡，表明上游坡是坝体稳定性的关键部位，应重点关注。

此外，图5给出了3种水位下土石坝内部的剪应变分布，剪应变反映了坝体在剪切力作用下所产生的相对形变量。分析可知，在校核洪水位时坝体发生剪应变的部位主要位于心墙底部偏上游位置，此时上游坡的稳定性良好；当水位下降至正常蓄水位时，发生剪应变的部位主要位于心墙与上游坝体的交界处，分布范围有限；而当水位下降至死水位时，心墙与上游坝体的交界处发生剪应变范围有所增大，存在往上游坡扩展的趋势，虽并未贯通，但不利于坝坡的稳定性。剪应变的变化趋势与表3坝坡的稳定性计算结果相符，即水位下降时土石坝的整体稳定性降低。

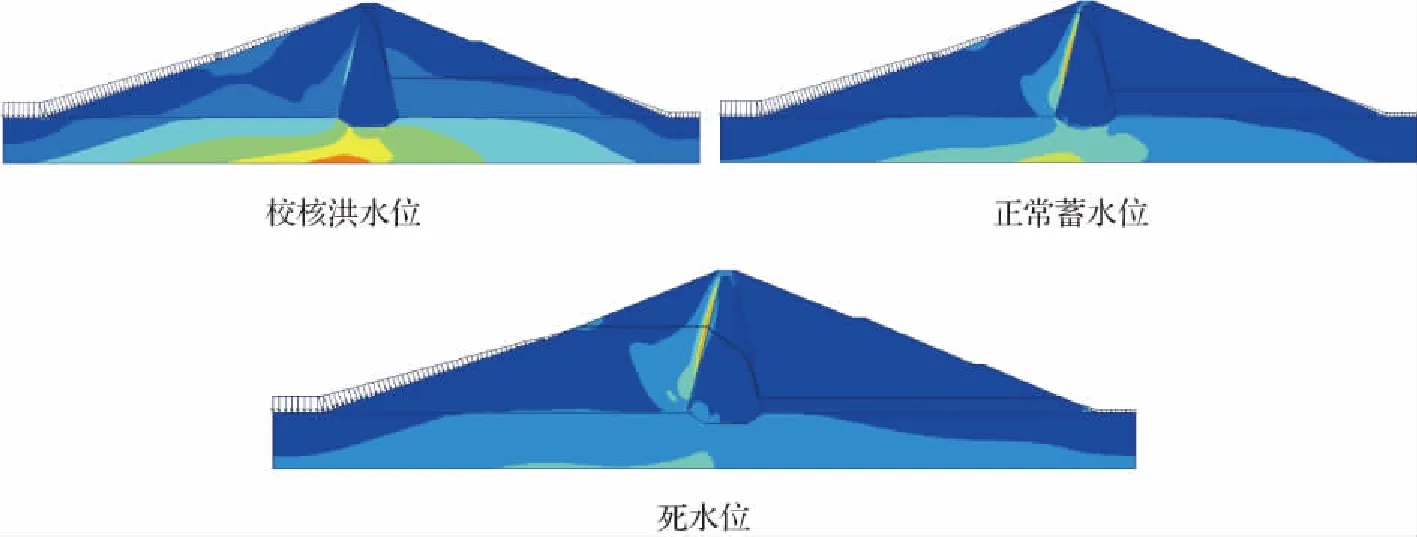
图5 不同特征水位坝体剪应变

4 结 论

本文基于渗流计算基本理论，计算了库水位下降过程中，各特征水位坝体内部浸润线、坝坡最小安全系数和坝体内部剪应变的变化规律。得到以下结论：

a.库水位下降导致上下游浸润线位置也逐渐降低，心墙内浸润线由直线变为折线。

b.随着水位的降低，下游溢出点高程也随之下降，而最大的渗流速度在校核洪水位工况时最大，为0.4503m/d，在正常蓄水位时最大渗流速度减小至0.2647m/d，库水位降低至死水位时最大渗流速度为0.2866m/d。3种水位下出现最大渗流速度的位置均位于浸润线出口部位。

c.上下游坝坡的最小安全系数Kmin随水位降低而减小，且上游坡稳定性小于下游坡，但均满足规范要求。

d.水位下降会造成心墙与上游坝体交界处的剪应变范围增大，并有向上游坝坡扩展的趋势。

[1] 王复来,陈洪天. 土石坝变形与稳定分析[M]. 北京:中国水利水电出版社,2008.

[2] 郑颖人. 岩土塑性力学的新进展—广义塑性力学[J].岩土工程学报, 2003, 25(1): 1-10.

[3] 黄传志. 土体极限分析的基本方程与广义极限平衡法[J]. 岩土力学, 2007,28(10):2127-2132

[4] 毛昶熙. 渗流计算分析与控制[M] . 北京:中国水利水电出版社, 2003.

[5] 赵振兴,何建京.水力学[M]. 北京:清华大学出版社,2010: 410-411．

[6] 徐中华,王卫东. 敏感环境下基坑数值分析中土体本构模型的选择[J]. 岩土力学,2010,31(1): 258-264

[7] DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis in limit design [J]. Quarterly of Applied Mathematics, 1952, 10(2): 157-165.

[8] 李宗坤, 何芳婵, 王建有,等. 基于ANSYS的土石坝施工过程仿真分析[J]. 人民黄河,2007,29(8):59-60

[9] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京：中国水利水电出版社，1980.

[10] 郑颖人, 赵尚毅, 张鲁渝. 用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10): 57-62.

[11] SL 274—2001碾压式土石坝设计规范[S]. 北京：中国水利水电出版社,2001.

AnalysisonwaterlevelfallingonPingshanReservoirclaycorewalldamseepagefieldandstability:

HU Shujuan

(Ji’anWaterConservancyandHydropowerPlanningandDesignInstitute,Ji’an343000,China)

In the paper, Pingshan Reservoir clay core wall dam is adopted as an example on the basis of basic theory of seepage in order to further study the influence of water level falling on earth rock dam seepage field and stability, the dam internal seepage line distribution and the minimum safety coefficient on the upstream and downstream dam slopes are obtained by calculation when the reservoir water level is decreased from checked flood water level to normal storage water level and dead water level. The results show that the seepage line is also gradually decreased with the decrease of reservoir water level, and the seepage line in the core wall is changed from a straight line to a folded line, and the maximum seepage speed during flood water level checking can be up to 0.4503m/d. The minimum safety coefficient on the upstream and downstream dam slopes is reduced with water level reduction, but they all meet the requirements in the specification. The shearing strain scope in the intersection between the core wall and the upstream dam is increased with water level reduction, and it has the trend of expansion to upstream dam line.

earth rock dam; core wall; seepage line; seepage; shear stress

10.16616/j.cnki.11- 4446/TV.2017.012.014

TV641.2

A

1005-4774(2017)012-0054-06