带滑移铰空间机器人运动规划的混合优化策略1)

姚其家 戈新生

(北京信息科技大学机电工程学院，北京100192)

带滑移铰空间机器人运动规划的混合优化策略1)

姚其家2)戈新生3)

(北京信息科技大学机电工程学院，北京100192)

研究了自由漂浮带滑移铰空间机器人非完整运动规划的最优控制问题，提出一种由高斯伪谱法求解可行解与直接打靶法求解最优解相结合的混合优化策略.首先，根据多体系统动力学理论建立空间机器人的动力学模型，给定系统的初始和目标位形，将空间机器人运动规划问题描述成博尔察(Bolza)型最优控制问题；然后，利用高斯伪谱法将最优控制问题离散为非线性规划问题，求解在较少勒让德--高斯 (Legendre--Gauss,LG)点时状态变量和控制变量对应的可行解；最后，在LG点处离散控制变量，作为直接打靶法的初值，利用序列二次规划算法求解空间机器人系统的优化运动轨迹和最优控制输入.通过数值仿真，系统优化运动轨迹光滑平稳，最优控制输入也能很好地满足各种约束条件，仿真结果验证了该混合优化策略的鲁棒性和有效性.

运动规划，空间机器人，滑移铰，高斯伪谱法，最优控制

随着航天技术的不断发展，空间机器人在人类的太空活动中扮演越来越重要的角色.自由漂浮是空间机器人常用的工作模式，由于机械臂与载体之间的动力学耦合作用，可以通过机械臂的关节运动实现载体的姿态改变，从而使载体和机械臂同时到达期望姿态.空间机器人系统的动量矩守恒方程不可积，使系统具有非完整约束的性质，大大增加了空间机器人系统的控制难度.

近年来，国内外学者对空间机器人的动力学与控制问题进行了广泛的研究，主要集中在运动规划、主动控制、轨迹跟踪和构型优化等方面[112].这些研究大都是针对带转动铰的空间机器人系统展开的.需要指出的是，尽管带转动铰的空间机器人具有更好的灵活性，但同时这类空间机器人系统的工作空间中存在着大量动力学奇点[1]，相比之下，滑移铰具备某些转动铰所没有的良好运动学性能[13].因此，对带滑移铰空间机器人系统的研究便显得十分必要，相关的研究工作还相对较少.陈力等[13-14]对带滑移铰空间机器人进行动力学建模，得到系统的广义雅可比(Jacobian)矩阵以及动力学方程，设计了一种自适应与鲁棒混合控制方案,对带滑移铰空间机器人进行轨迹跟踪.厉虹等[15]将带滑移铰空间机器人的姿态运动规划问题转化为非线性规划问题，再利用遗传算法进行求解.该方法具有很好的全局搜索能力，但存在早熟收敛等遗传算法的固有缺陷.郭益深等[16]基于双向逼近的李雅普诺夫(Lyapunov)方法，讨论了自由漂浮带滑移铰空间机器人的运动规划问题.使用该方法得到的控制方程存在病态域，在实际操作中需要对控制方程的参数进行修正.

本文研究带滑移铰空间机器人系统非完整运动规划的最优控制问题，提出一种高斯 (Gauss)伪谱法和直接打靶法相结合的混合优化策略.首先，利用动量及动量矩守恒关系，建立空间机器人系统的动力学模型，给定系统的初始和目标位形，选择机械臂各关节的耗散能作为优化性能指标，将空间机器人运动规划问题描述成博尔察(Bolza)型最优控制问题；然后，利用高斯伪谱法将连续的最优控制问题离散为非线性规划问题，选取较少的勒让德--高斯(Legendre--Gauss,LG)点，求解状态变量和控制变量的可行解，可行解的求解采用串行优化策略；最后，在 LG点处利用线性插值离散控制变量，作为直接打靶法的初值，利用序列二次规划 (sequential quadratic programming,SQP)算法求解空间机器人系统的优化运动轨迹和最优控制输入.文末给出仿真算例.

1 动力学建模

作平面运动的带滑移铰三刚体空间机器人系统如图1所示.系统由自由漂浮的载体B0、机械臂前杆B1和末杆 B2组成，其中，分体 B0和B1之间通过转动铰联结，B1和B2之间通过滑移铰联结.

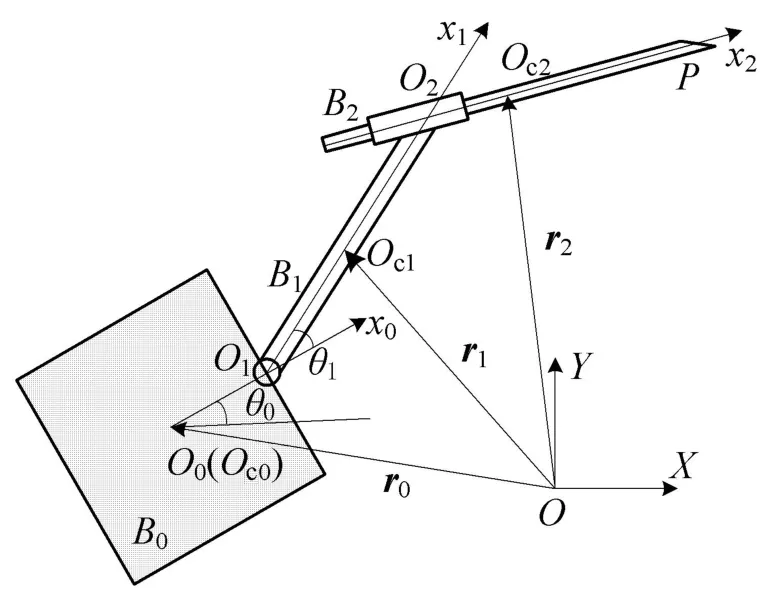
图1 带滑移铰空间机器人系统

以系统总质心 O为原点建立惯性坐标系 OXY. 建立分体 Bi(i=0,1,2)的连体坐标系Oi−xiyi，其中，O0与B0的质心Oc0重合，O1为联结分体B0和B1的转动铰中心，O2为联结分体B1和B2的滑移铰中心.设O1沿x0轴与O0之间的距离为l0，Bi(i=1,2)沿其连体坐标系xi轴的长度为li(i=1,2).各分体的质量和中心转动惯量分别为 mi和 Ii(i=0,1,2)，m 为系统的总质量.x0轴相对 X 轴的转角为θ0,x1轴相对x0轴的转角为θ1，x2轴相对x1轴的转角为θ2，这里θ2为常值.设B2末端点P沿x2轴与O2之间的距离为x′.作平面运动的带滑移铰空间机器人系统具有3个自由度，选择 θ0,θ1和 x′作为系统的广义坐标.根据图示几何关系，各分体质心Oci(i=0,1,2)相对系统总质心O的位置矢量ri表示为

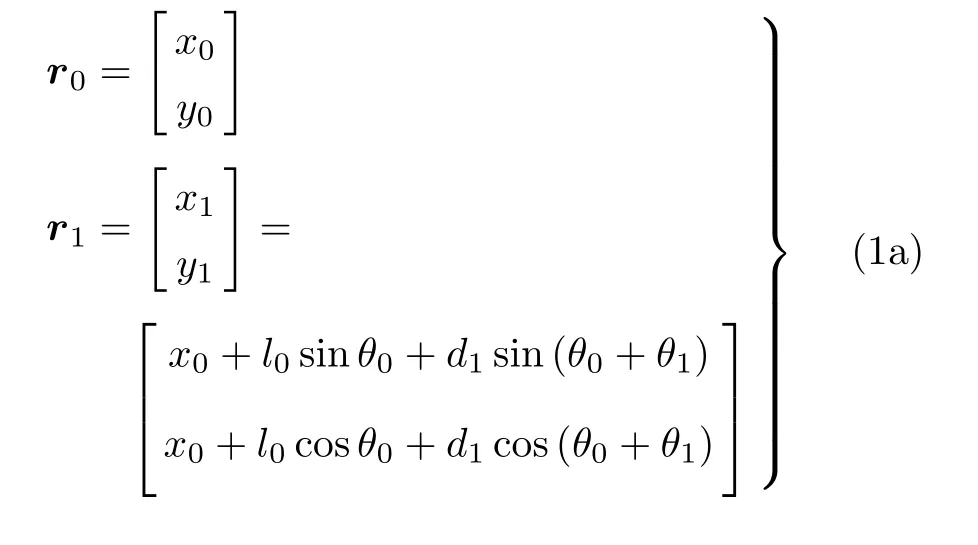
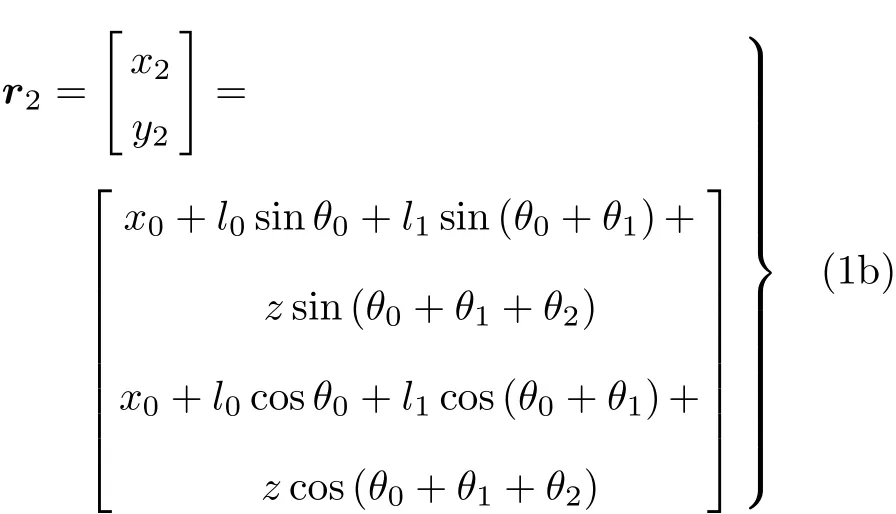
式中，d1=l1/2，z=x′−l2/2.根据系统质心运动定理和式(1a)和式(1b)可得

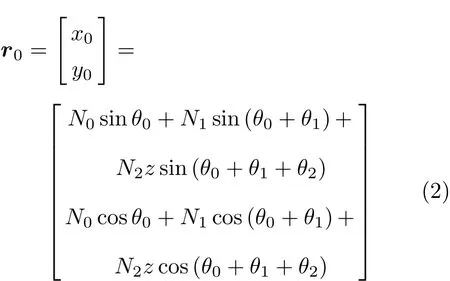
式中，N0= −(m1l0+m2l0)/m,N1= −(m1d1+m2l1)/m,N2=−m2/m.将式 (2)代入式 (1)消去x0和 y0,得到 ri的最终表达式.再对时间求导，得到各分体质心Oci相对系统总质心O的速度˙ri(i=0,1,2)的表达式.

设系统的初始动量矩为零，根据系统动量矩守恒关系，有

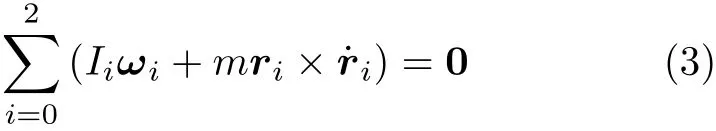
式中，ωi(i=0,1,2)为分体 Bi的绝对角速度,大小如下

将ri和˙ri的最终表达式和式(4)代入式(3)，得到空间机器人系统的动力学方程

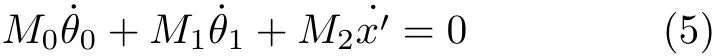
式中，M0，M1和 M2为 θ0，θ1和 x′的函数，具体表达式参见附录1.

2 最优控制方法

2.1 最优控制问题

不失一般性，将空间机器人系统运动规划问题描述为Bolza型最优控制问题.定义系统的位形x=[θ0,θ1,x′]T为状态变量.由于载体的位置和姿态均不受控，选择空间机器人的关节速度˙θ1和˙x′作为系统的控制变量，即系统的状态方程由式(5)得到

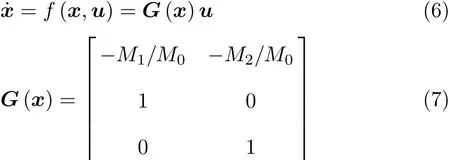
根据最小能量控制原理，选择空间机器人系统各关节的耗散能作为最优控制指标，相应的目标函数表示为

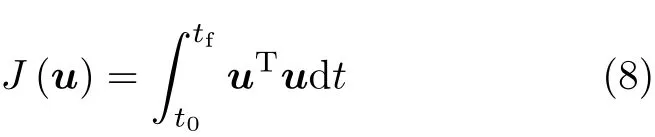
边界条件约束包括空间机器人系统运动过程初末端的位形约束和控制输入约束

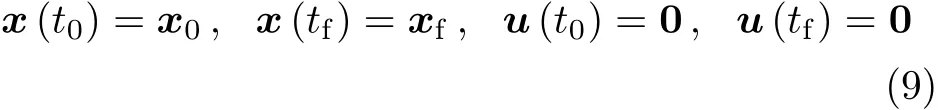
在实际操作中，还需考虑空间机器人系统关节变量的变化范围以及控制输入受限等不等式路径约束

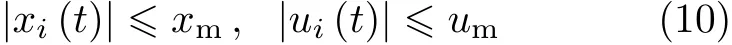
式中，xm和um分别表示空间机器人系统关节变量和控制输入的上界.

2.2 高斯伪谱法

高斯伪谱法是一种直接优化方法，采用全局插值多项式在LG点近似状态变量和控制变量，将连续的最优控制问题转化为代数约束形式的参数优化问题，即非线性规划问题[17].

最优控制问题的时间区间为[t0,tf]，而采用高斯伪谱法需要将时间区间转换到[−1,1]，对时间变量t作如下变换

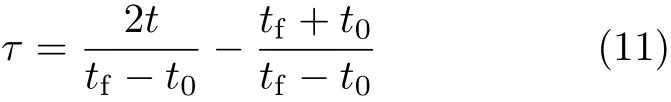
取 K 个 LG 配点 τi(i=1,2,···,K)以及 τ0= −1作为离散节点，构成K+1个拉格朗日插值多项式的基函数 Li(τ)(i=0,1,···,K) 来近似状态变量，即

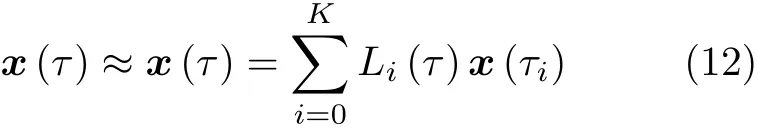
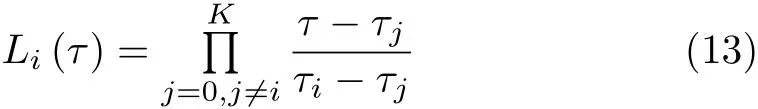
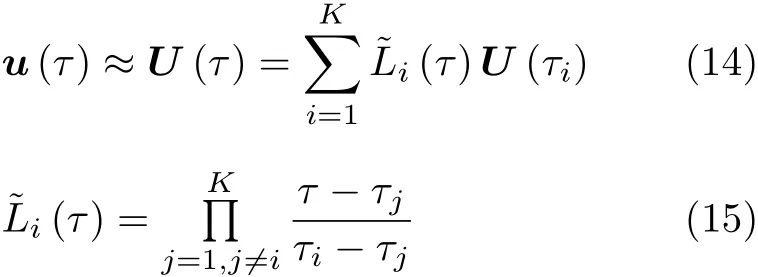
将终端状态表示成离散状态变量和控制变量的积分形式，再利用高斯积分近似可得

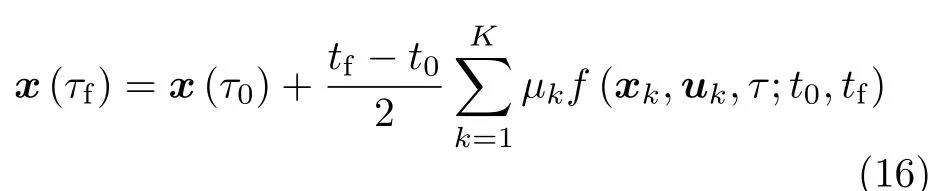
状态方程的导数用式(12)的导数作近似处理，即

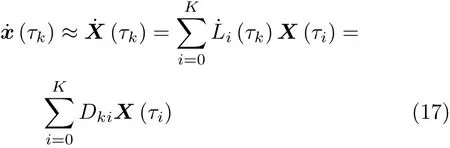
式中，微分矩阵D∈RK×(K+1)由式(18)确定[18]

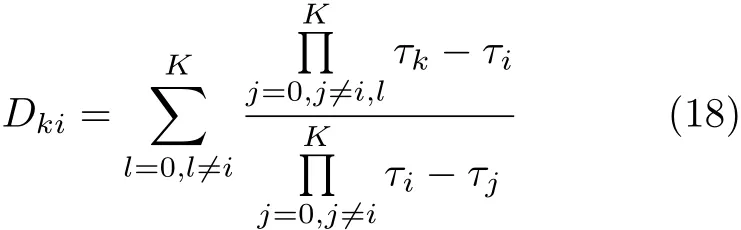
将式(17)代入状态方程(6)得到状态方程在配点处的离散表达形式

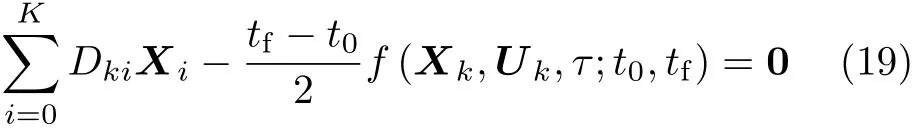
式中，k=1,2,···,K.Xk≡ X(τk)，Uk≡ U(τk).

用高斯积分近似最优控制问题中目标函数式(8)的积分项，得到离散形式的近似目标函数为

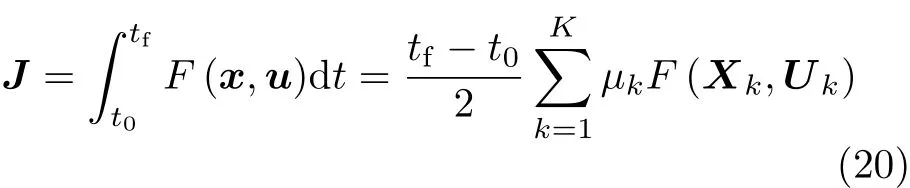
2.3 直接打靶法

直接打靶法是一种仅离散控制变量的直接优化方法[19].它将连续时间离散为K段以离散时间节点上相对应的控制变量

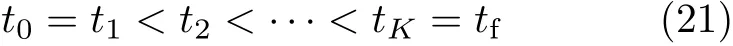
为设计变量，给定一组设计变量的值，通过插值获取相邻节点之间的控制变量的值，再代入状态方程积分得到状态变量，进而求解目标函数和约束条件.

通过上述过程，将空间机器人系统最优控制问题离散为代数约束形式下的非线性规划问题，即：通过求解离散控制变量y，使得性能指标(20)最小，并满足状态约束方程(19)、终端状态约束(16)、边界条件约束(9)和不等式路径约束(10).非线性规划问题采用SQP算法进行求解，SQP算法通过MATLAB软件包SNOPT实现.

2.4 混和优化策略

利用高斯伪谱法求解最优控制问题，若LG点选取较少，则得到的结果精度较差.若LG点选取较多，则设计变量的数目庞大，计算量成倍增长.如果变量初值选取不当，往往会使问题收敛不到可行解或陷入局部最小化而得不到全局最优解.针对这一问题，本文只利用高斯伪谱法生成可行解.

首先选取较少的LG点K，利用高斯伪谱法将空间机器人系统姿态最优控制问题转化为非线性规划问题，利用SQP算法求解状态变量和控制变量的可行解.高斯伪谱法可以在较少的节点获得较高的精度，且此时需要赋初值的设计变量较少，操作比较方便.

对于可行解的求解，采用从可行解到近似最优解的串行优化策略[20].首先不考虑实际性能指标，将等式约束变换后作为目标函数，求得可行解；然后将可行解作为初值，代入原有控制问题求得近似最优解.这种方法可使程序更有效地收敛.

利用选取的 LG点将时间离散，将相邻的 LG点之间的时间再 N 等分，整个运动过程离散为(K+1)N段.将得到的 (K+1)N个控制变量的值作为直接打靶法的初值，利用SQP算法求解精度更高的最优解.LG点处的控制变量的初值通过高斯伪谱法得到，等分点处的控制变量的值通过三次样条函数插值求得.

混合优化策略结合了高斯伪谱法和直接打靶法的优点，对变量初值不敏感，收敛速度快，并且具有很高的求解精度.图2给出了空间机器人系统混合优化策略的具体流程.

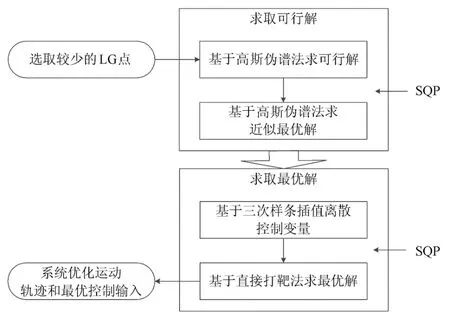
图2 混合优化策略具体流程

3 数值仿真

以带滑移铰空间机器人的运动规划问题作为仿真算例.系统的质量几何参数分别为：l0=0.5m，l1=1m，l2=1m，θ2= π/3；m0=30kg，m1=1kg，m2=1kg；I0=2.340kg·m2，I1=0.084kg·m2，I2=0.072kg ·m2.

算例 1 空间机器人系统载体 B0由初始位形 π/9逆时针转到终端位形 5π/6，机械臂前杆 B1由初始位形 π/18逆时针转到终端位形 2π/9，末杆B2由初始位形 0.48m 沿滑移铰运动到终端位形−0.45m，即空间机器人系统的初始和终端位形分别为

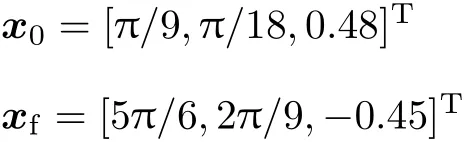
计算采用前文所述的混合优化策略，选取LG节点个数 K=6，利用高斯伪谱法计算可行解，在相邻的LG点处将轨道离散为5段，即取N=4，利用直接打靶法计算最优解，设置仿真时间t=1.5s.仿真结果如图 3和图 4所示.图 3为空间机器人位形θ0，θ1和x′的优化轨迹，轨线光滑平稳，并且满足空间机器人初末位置的位形约束.从图中还可以看出，载体姿态角θ0从初始姿态沿顺时针运动到−π，再沿逆时针运动到达末端指定姿态，机械臂关节角θ1从初始姿态沿逆时针运动到近π/3，再沿顺时针运动到达末端指定姿态.将本文仿真结果与文献[16]采用双向逼近方法得到的结果进行比较，θ0和θ1的运动轨迹基本一致，也说明本文提出的混合优化策略是可行的.图4为空间机器人关节最优控制输入规律，最优控制输入满足控制输入限制，且初始和终端时刻控制输入均为0.

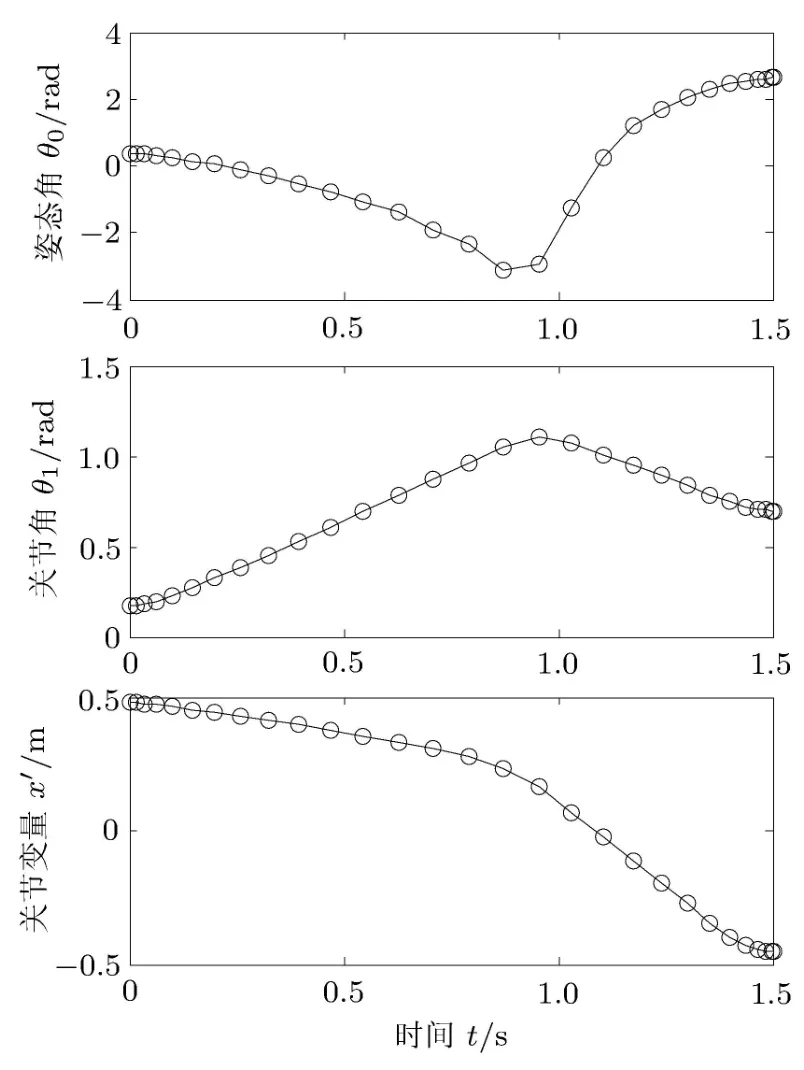
图3 空间机器人优化运动轨迹(算例1)

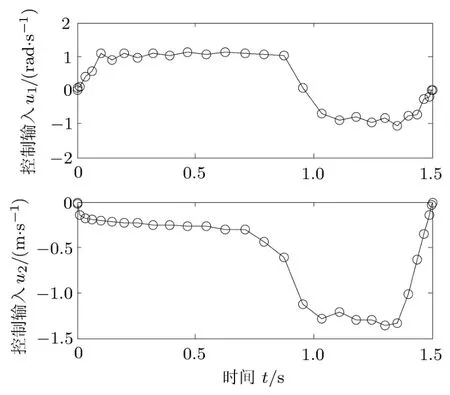
图4 空间机器人最优控制输入(算例1)

混合优化策略采用 MATLAB编程，计算在CPU为2.5GHz/Core i3，内存4.0G的windows 10计算机上进行，整个优化过程用时90s左右，目标函数最优值J=2.766.表1给出了选取5组不同初值时，最优解相关参数的变化情况.其中，初值是采用MATLAB的随机函数在约束区间内随机生成的.

表1 不同初值下的最优解相关参数

从表1可以看出，每次最优解的求解采取不同的随机初值，优化性能指标J的变化幅度不大，由此可见，本文提出的混合优化策略具有很好的鲁棒性.

算例 2 空间机器人系统载体B0的初始和终端位形保持π/2不变，机械臂前杆B1由初始位形π/18逆时针转到终端位形 π/9，末杆 B2由初始位形0.30m沿滑移铰运动到终端位形−0.20m，即空间机器人系统的初始和终端位形分别为

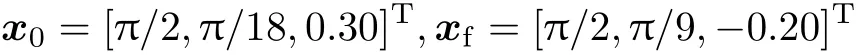
仿真结果如图5和图6所示.图5为空间机器人系统优化运动轨迹，其中，载体姿态角θ0和机械臂关节角θ1的变化趋势与算例1基本相同.图6为空间机器人系统关节最优控制输入.整个优化过程用时75s左右，目标函数最优值J=2.919.从仿真结果可以看出，以关节角速度作为控制输入信号，空间机器人系统的姿态和运动都是可控的，且优化运动轨线和最优控制输入都能很好地满足空间机器人系统的运动要求.

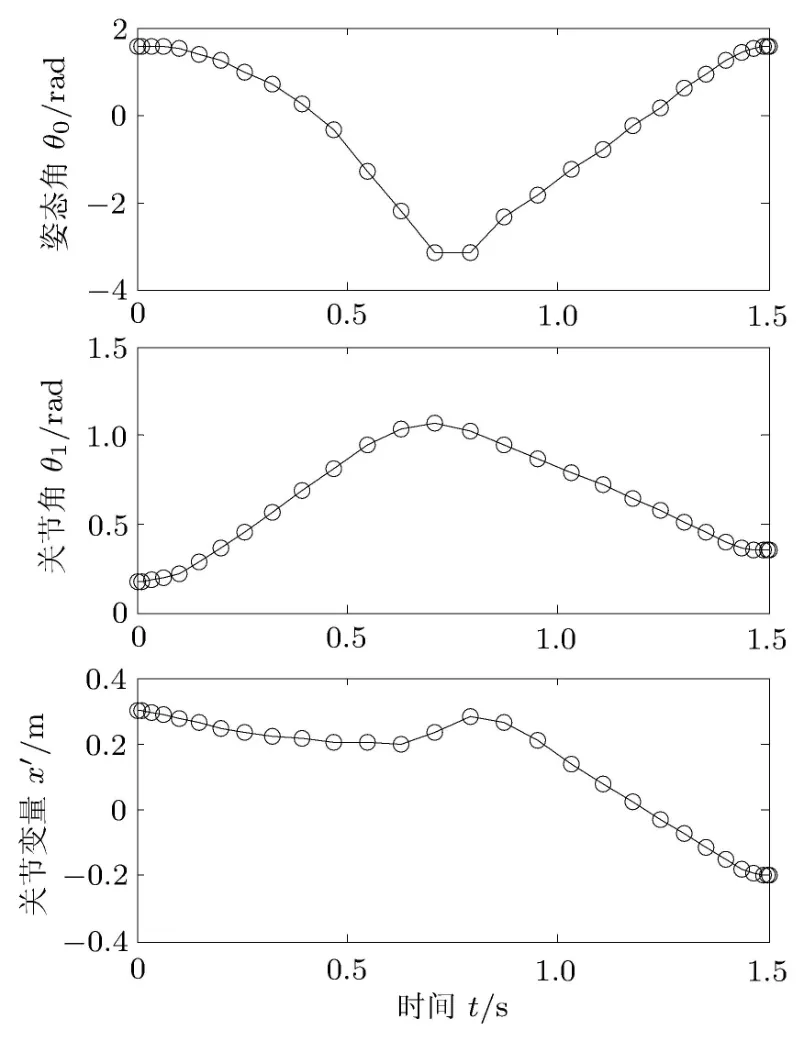
图5 空间机器人优化运动轨迹(算例2)

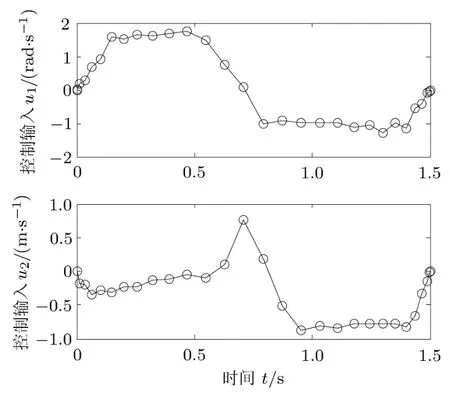
图6 空间机器人最优控制输入(算例2)

4 结论

本文结合高斯伪谱法和直接打靶法研究了带滑移铰空间机器人的姿态运动规划问题.仿真结果表明，空间机器人系统优化运动轨迹光滑平稳，控制输入能够很好地满足各种约束条件，混合优化策略对初值具有很好的鲁棒性.尽管本文工作针对空间机器人系统非完整运动规划问题展开，但提出的基于高斯伪谱法和直接打靶法的非完整系统运动规划数值方法也为其他优化控制问题提供了一种求解思路.

1 Dubowsky S,Papadopoulos EG.The kinematics,dynamics and control of free- flying space robotic systems.IEEE Transactions on Robotics and Automation,1993,9(4):531-543

2 Boning P,Dubowsky S.A kinematic approach to determining the optimal actuator sensor architecture for space robots.The International Journal of Robotics Research,2011,30(9):1194-1204

3 Kumar A,Pathak PM,Sukavanam N.Trajectory control of a two DOF rigid- flexible space robot by a virtual space vehicle.Robotics and Autonomous Systems,2013,61:473-482

4 Pisculli A,Felicetti L,Gasbarri P,et al. A reactionnull/Jacobian transpose control strategy with gravity gradient compensation for on-orbit space manipulators.Aerospace Science and Technology,2014,38:30-40

5 Ulrich S,Sasiadek JZ,Barkana I.Nonlinear adaptive output feedback control of flexible-joint space manipulators with joint stiffness uncertainties. Journal of Guidance,Control,and Dynamics,2014,37(6):1961-1975

6 Nanos K,Papadopoulos E.Avoiding dynamic singularities in Cartesian motions of free- fl oating space manipulators.IEEE Transactions on Aerospace and Electronic Systems,2015,51(3):2305-2318

7 Rybus T,Seweryn K,Sasiadek JZ.Control system for free floating space manipulator based on nonlinear model predictive control(NMPC).Journal of Intelligent and Robotic Systems,2017,85:491-509

8戈新生,陈凯捷.自由漂浮空间机器人路径优化的Legendre伪谱法.力学学报,2016,48(4):823-831

9廖一寰,李道奎,唐国金.基于混合规划策略的空间机械臂运动规划研究.宇航学报,2011,32(1):98-103

10徐文福,王学谦,薛强等.保持基座稳定的双臂空间机器人轨迹规划研究.自动化学报,2013,39(1):69-80

11戴巧莲,陈力.基于干扰观测器的柔性关节空间机器人退步自适应控制.力学与实践,2016,38(4):386-390

12郭闻昊,王天舒.空间机器人捕获目标星碰撞前构型优化.宇航学报,2015,36(4):390-396

13陈力,吴文龙,刘延柱.带滑移铰空间机械臂的分解运动速度控制.力学与实践,2000,22(6):28-31

14陈力.带滑移铰空间机器人惯性空间轨迹跟踪的鲁棒混合自适应控制.工程力学,2004,21(3):174-179

15厉虹,胡兵.带滑移铰空间机械臂的非完整运动规划遗传算法.微计算机信息,2006,22(4):177-179

16郭益深,陈力.带滑移铰空间机械臂运动规划的双向逼近方法.力学与实践,2006,28(1):28-31

17唐国金,罗亚中,雍恩米.航天器轨迹优化理论、方法及应用.北京:科学出版社，2012

18 Benson DA.A Gauss pseudo spectral transcription for optimal control.[PhD Thesis].Cambridge:Massachusetts Institute of Technology,2005

19雍恩米,陈磊,唐国金.飞行器轨迹优化数值方法综述.宇航学报,2008,29(2):397-406

20易中贵,戈新生.自由下落猫姿态最优控制的混合优化策略.力学学报,2016,48(6):390-397

附录1

式(5)中M0，M1和M2的具体表达式为

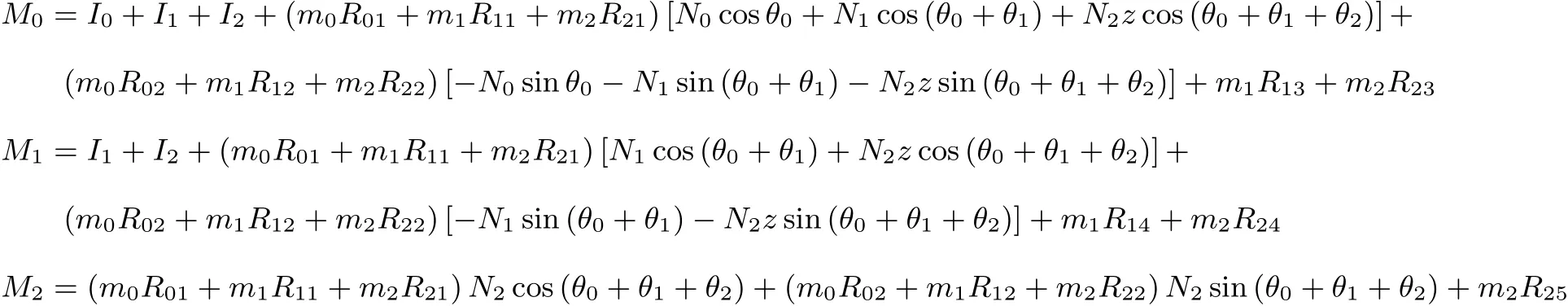
式中，N0，N1和N2的表达式参见正文公式(2)，其余参数的表达式如下

HYBRID OPTIMIZATION STRATEGY FOR MOTION PLANNING OF SPACE ROBOT SYSTEM WITH PRISMATIC JOINT1)

YAO Qijia2)GE Xinsheng3)
(School of Mechanical&Electrical Engineering，Beijing Information Science&Technology University，Beijing 100190，China)

This paper studies the optimal control of the nonholonomic motion planning for the free- floating space robot with prismatic joint.A hybrid optimization strategy based on the Gauss pseudospectral method(GPM)and the direct shooting method(DSM)is proposed.First,a dynamics model for the space robot is established based on the multibody dynamics theory.For a given initial and final configurations,the motion planning problem is described as an optimal control problem in the Bolza form.Then,the continuous optimal control problem is transformed into a nonlinear programming problem based on the GPM.With fewer Legendre--Gauss (LG)points,the feasible solution of the state variables and the control variables can be obtained.Finally,the control variables are discretized at the LG points and used as the initial values of the DSM,the optimal trajectory and the optimal control inputs are obtained by the sequential quadratic programming(SQP)algorithm.As shown by the numerical simulation,the optimal trajectory of the system is stable with no detours,and the control inputs match the various constraints under actual conditions.The results indicate that the hybrid optimization strategy is effective with a good robustness.

motion planning,space robot,prismatic joint,Gauss pseudospectral method,optimal control

2017–04–12收到第1稿，2017–07–04 收到修改稿.

1)国家自然科学基金资助项目(11472058).

2)姚其家，硕士研究生，主要从事航天器姿态动力学与控制的研究.E-mail:qijia-yao@126.com

3)戈新生，通讯作者，博士，教授，主要从事多体系统动力学的教学和科研工作.E-mail:gebim@vip.sina.com

姚其家,戈新生.带滑移铰空间机器人运动规划的混合优化策略.力学与实践,2017,39(6):566-572

Yao Qijia,Ge Xinsheng.Hybrid optimization strategy for motion planning of space robot system with prismatic joint.Mechanics in Engineering,2017,39(6):566-572

TP241

A

10.6052/1000-0879-17-122

(责任编辑:周冬冬)