基于位移不连续模型的多裂缝应力干扰极限距离计算
闫相祯, 董 卫, 樊 恒, 闫怡飞, 许建国,4
(1.中国石油大学油气CAE技术研究中心,山东青岛 266580; 2.中国石油大学机电工程学院,山东青岛 266580;3.西安石油大学电子工程学院,陕西西安 710000; 4.中国石油吉林油田分公司,吉林松原 138000)
基于位移不连续模型的多裂缝应力干扰极限距离计算
闫相祯1, 董 卫2, 樊 恒3, 闫怡飞2, 许建国1,4
(1.中国石油大学油气CAE技术研究中心,山东青岛 266580; 2.中国石油大学机电工程学院,山东青岛 266580;3.西安石油大学电子工程学院,陕西西安 710000; 4.中国石油吉林油田分公司,吉林松原 138000)
利用MTS试验装置对“R13区块”的致密砂岩岩心进行小试样试验,获得“R13区块”致密砂岩的岩石力学参数(弹性模量、泊松比等)。忽略地层内水力裂缝面的不规则性,将其简化为互相平行的光滑裂缝面。考虑到地层在裂缝面的不连续性,将裂缝视为连续地层的内部不连续边界,采用位移不连续理论建立边界元模型,研究多裂缝系统周围的地层应力分布和不同簇数、不同布缝方式下的裂缝群缝间应力干扰的极限距离。结果表明,人工多裂缝的出现明显改变了裂缝周围应力场的分布,裂缝群簇数越多影响距离越大,但簇数的增加对影响距离的改变逐渐趋于平缓,呈对数增长,而段内裂缝间距(20~30 m)的改变基本不影响应力干扰的极限距离。基于位移不连续理论的边界元模型能够准确地计算裂缝群周围地层应力场分布和裂缝群缝间应力干扰极限距离。
多裂缝; 应力干扰; 位移不连续理论; 极限距离
作为低渗透油气井增产的主要措施,水平井分段多簇压裂技术越来越受到重视。近几年川庆钻探、勘探开发研究院、吉林油田自主研发了水平井裸眼分隔器分段压裂工具,现场成功试验百余口井,已发展成为水平井分段压裂改造的主体技术[1];同时,对水平井分段压裂技术机制的研究也成为了重要课题。大量的现场和室内试验研究表明[2-10],油气井压裂后,人工裂缝的存在能改变近井地带地应力的大小和方向。随着水平井压裂段数和簇数的增加,缝间应力干扰受到重视,合理地利用缝间应力干扰可以改变裂缝起裂方向,提高储层改造效果,但同时也会因为缝间的应力干扰形成局部高应力,影响储层改造[11-13]。为优化水平井段的段间距和簇间距,须对地层人工裂缝群周围应力场的分布进行细致研究。笔者通过对R13区块致密砂岩岩心进行力学试验,获得R13区块岩石的力学参数,采用位移不连续理论计算该区块分段压裂产生的裂缝群对地应力分布影响的极限距离。
1 岩心力学试验

图1 MTS岩石试验系统Fig.2 MTS rock-testing system
为准确获取R13区块致密砂岩的岩石力学参数,利用MTS试验系统(图1)对R13区块的致密砂岩岩心进行了常规力学试验。根据国际岩石力学学会(ISRM)推荐的方法,将钻取岩心制成直径为25 mm,高为50 mm的圆柱型试件,如图2所示。其端面不平行度不超过0.05 mm,直径误差不超过0.3 mm,尺寸测量精度为0.1 mm。根据油藏埋深地应力选取围压为35 MPa。绘制R13区块岩心应力-应变曲线如图3所示。

图2 砂岩岩心试件Fig.2 Specimens of sandstone cores
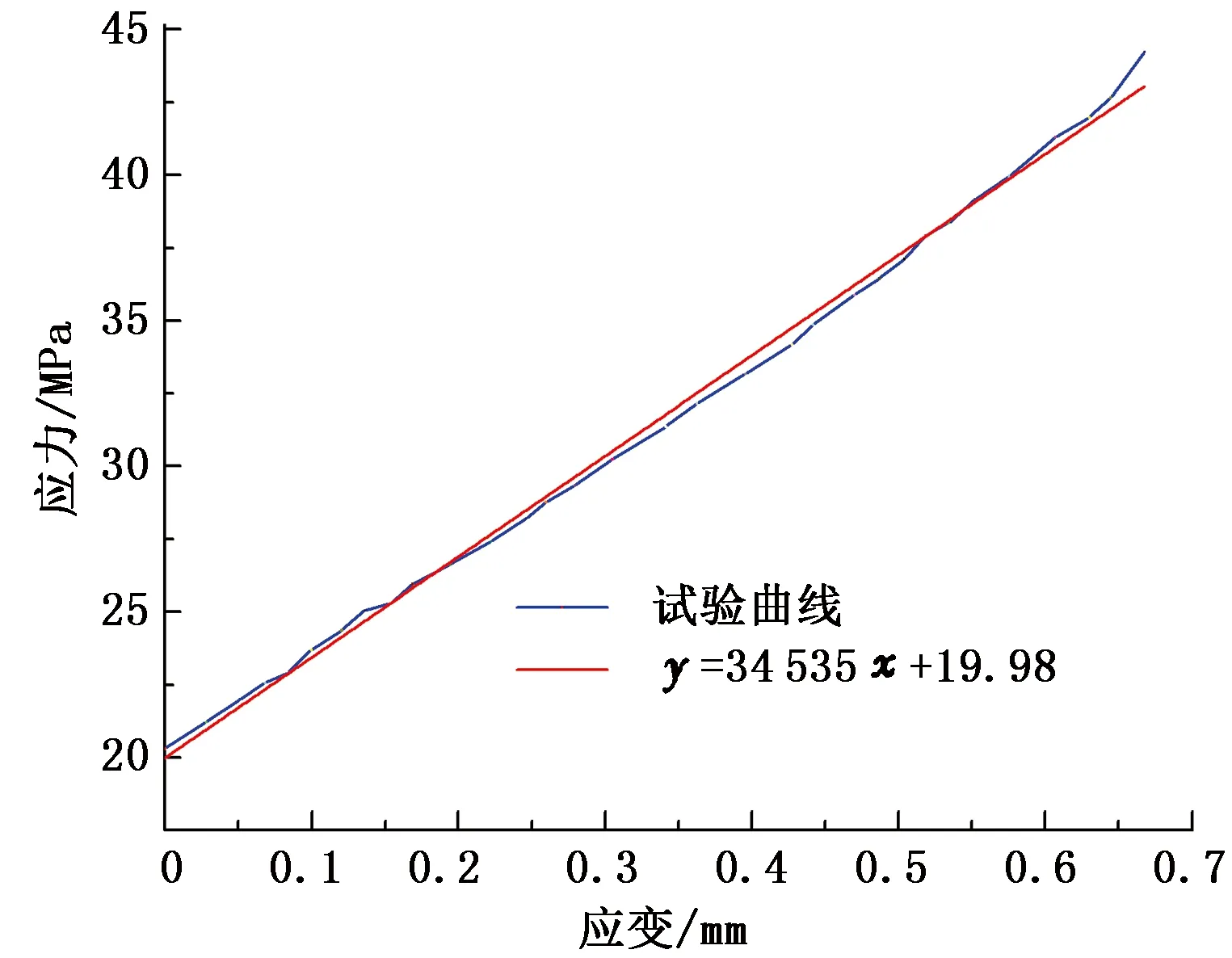
图3 砂岩岩心应力-应变曲线Fig.3 Stress-strain curves of sandstone
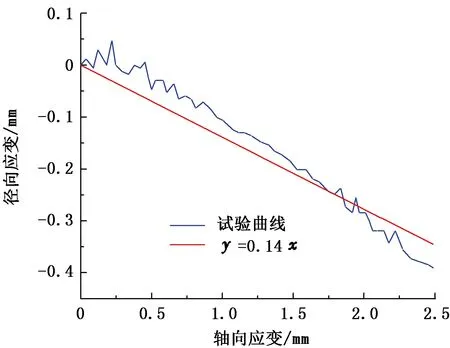
图4 径向-轴向应变曲线Fig.4 Radial-axial strain curves
通过岩心力学试验,对试验结果进行线性拟合,试验结果如图3、 4所示。图中蓝色线表示试验数据,红色直线为线性拟合结果。R13区块的岩心弹性模量为34.6 GPa,泊松比为0.14。通过力学试验得到R13区块的岩石力学参数,为后续裂缝应力干扰极限的研究提供了基础数据。
2 位移不连续理论基本解
位移不连续法是由美国学者Crouch于1973年在国际岩石力学会议上第一次提出,并给出了位移不连续理论的二维解[14-16]。迄今为止,已有大量的学者运用位移不连续理论进行岩石力学问题的研究[17-18]。Kresse和Wu等[19-20]采用改进的二维位移不连续法研究裂缝扩展问题。
当进行水力压裂时,地层中会出现水力裂缝,裂缝的上下表面间会发生相对位移和错动,即为所说的位移不连续量。故而将裂缝的两个面视为地层内部的不连续边界。建立长为2l的不连续单元如图5所示。裂缝面x与y方向的不连续量分别用Dx、Dy表示,相对的单个面的位置则用u(x,0-)、u(x,0+)、u(y,0-) 、u(y,0+)表示。裂缝面的位移不连续量可以表示为
Dx=ux(x,0-)-ux(x,0+),
Dy=uy(y,0-)-uy(y,0+),|x|≤l.
(1)
式中,正号表示上表面,负号表示下表面;裂缝张开Dy为负。
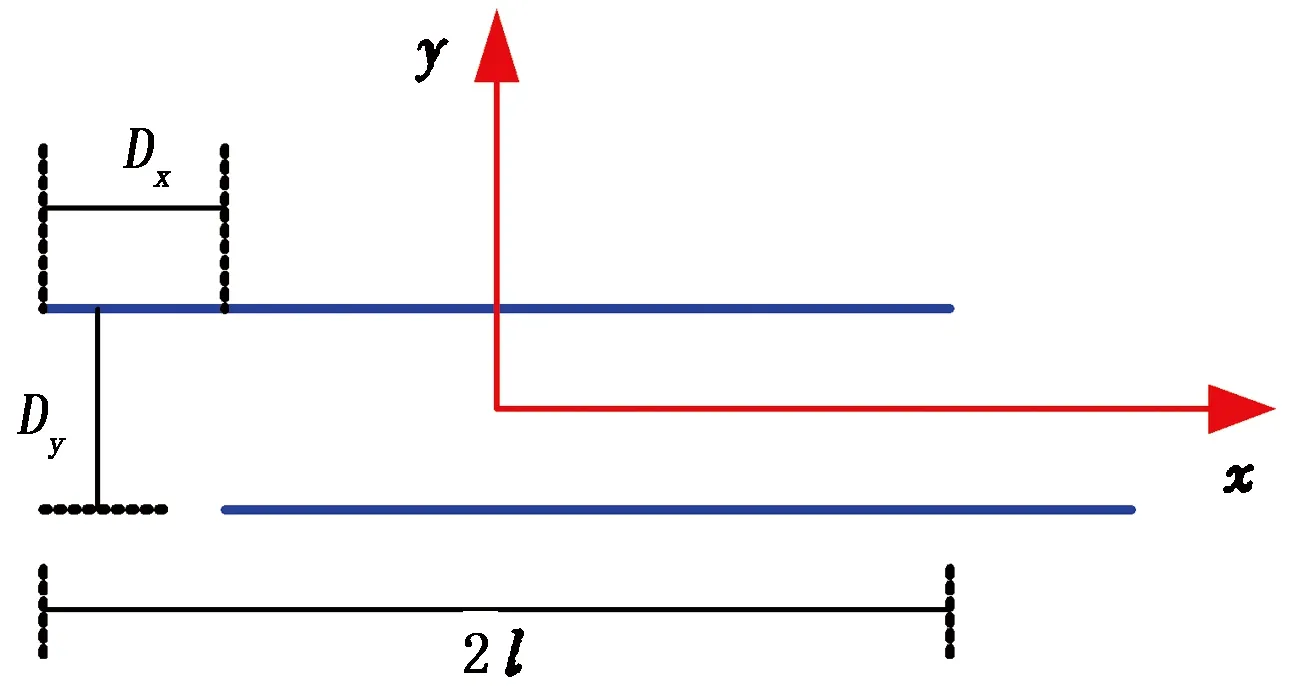
图5 二维位移不连续单元Fig.5 Two-dimensional displacement discontinuity element
Crouch和Starfied给出了计算位移和地应力的计算公式[15]如下:
(2)
式中,ux为水平位移;uy为垂直位移;Dx为切向不连续位移;Dy为法向不连续位移。
f是与点的位置坐标有关的函数,表述为
(3)
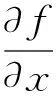
(4)
(5)
(6)
(7)
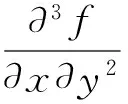
(8)
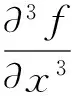
(9)
则x与y方向的应力及剪应力表达式为
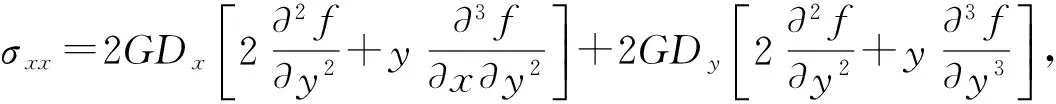
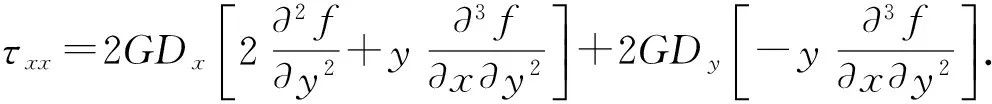
(10)
3 R13区块裂缝群间应力影响范围分析
依据位移不连续原理,采用R13区块的岩心试验结果,对R13区块的裂缝间应力干扰进行了研究。
3.1 模型建立
水平井每段簇数分别为2、3、4、5、6簇。图6为多裂缝压裂过程的产层受力示意图。模拟计算中,产层模型尺寸取800 m×400 m,裂缝长度为100 m,井眼位置位于裂缝中间;AB、CD加载最大水平主应力σH;AB、BC边加载最小主应力σh;初始地层压力为p0。
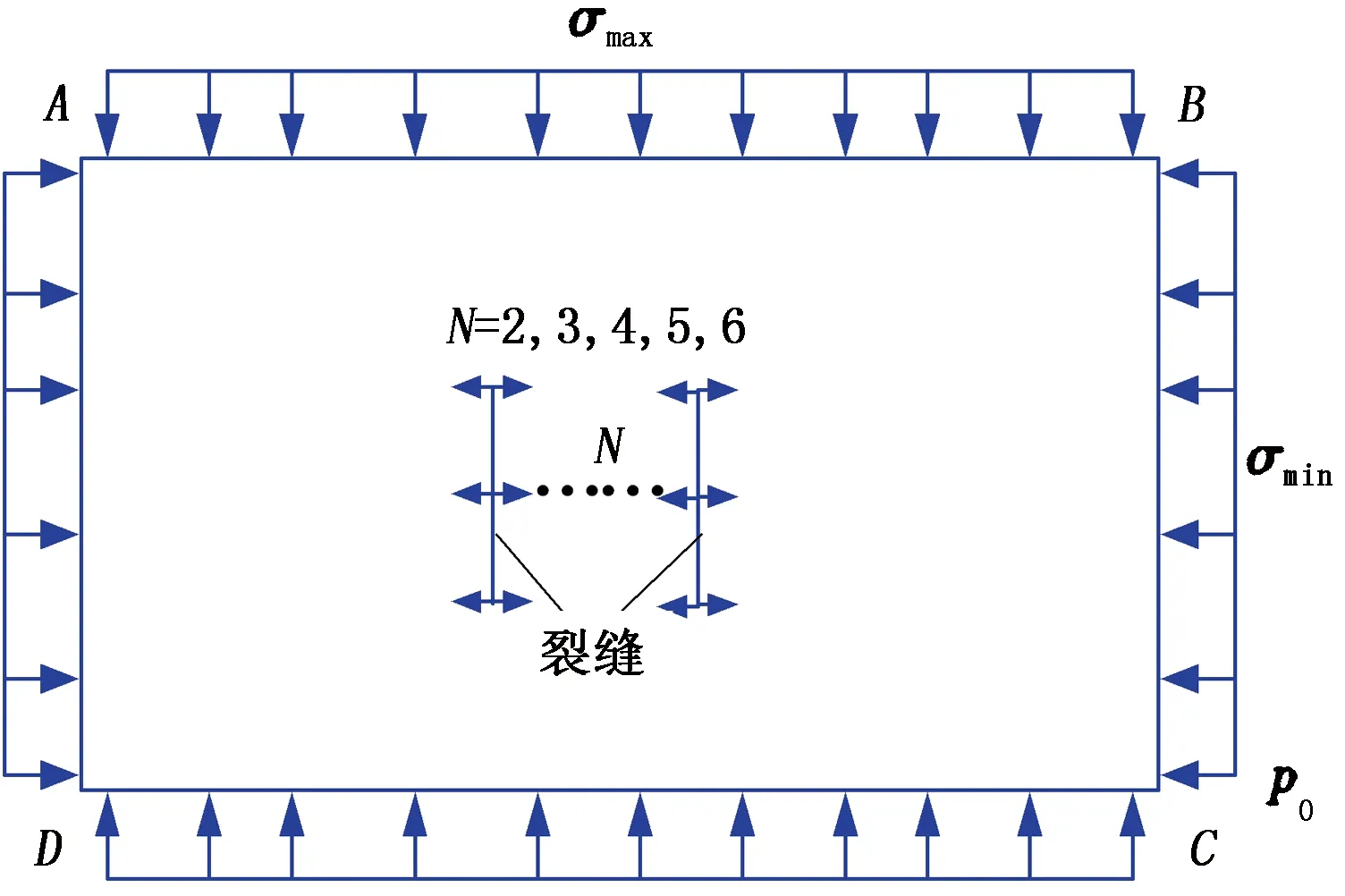
图6 地层受力示意图Fig.6 Diagram of strata stress
有限元模型尺寸为600 m×1 000 m,裂缝长度为100 m,最大、最小水平地应力分别为24 和20 MPa,砂岩弹性模量为34.6 GPa,泊松比为 0.14,地层孔隙压力为19 MPa,地层孔隙度为9%。结合水平井压裂射孔工具,簇间裂缝间距取25 m。
3.2 计算结果分析
为更直观地看出地层应力改变区域,将计算结果制成云图如图7、8所示。结合工程实际,当应力改变值小于5%时,认为地层应力值未发生变化,即为图中蓝色区域。
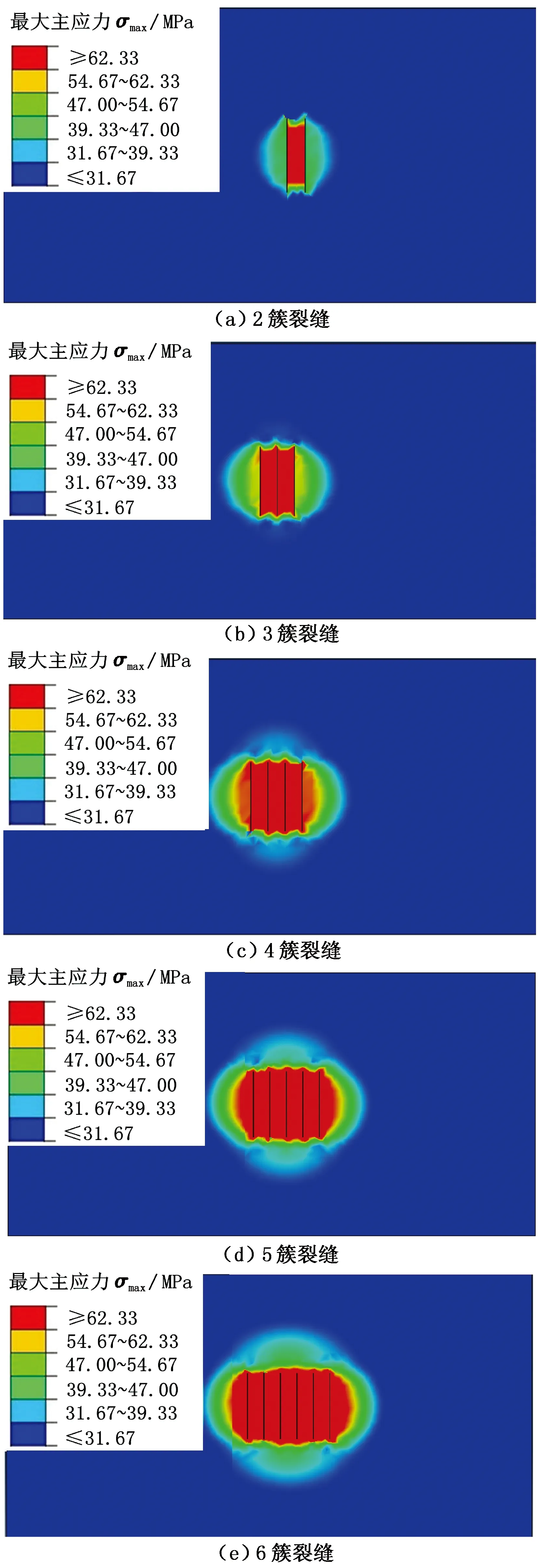
图7 不同簇数下地层最大主应力云图Fig.7 Maximum main stress nephogram under different clusters
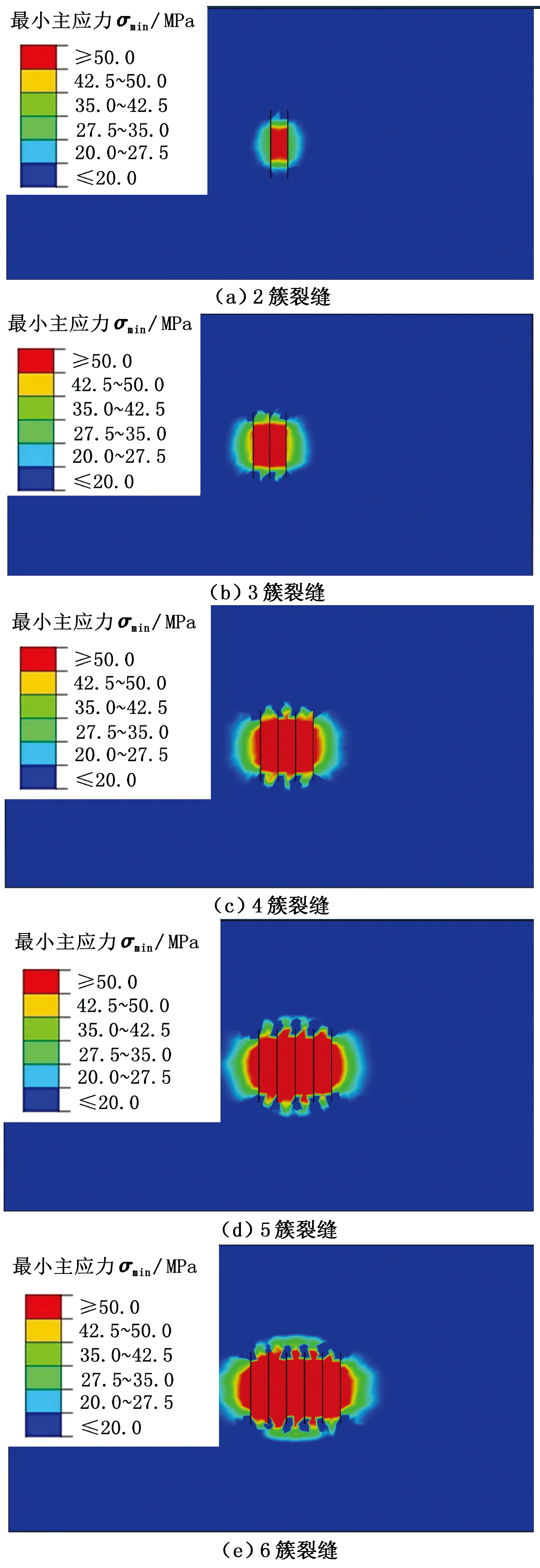
图8 不同簇数下地层最小主应力云图Fig.8 Minimum main stress nephogram under different clusters
从图7和图8可以得出,最大主应力和最小主应力的影响范围均随着压裂簇数的增加而增加。将图中数据提取作成曲线如图9所示。由图9可以看出,在裂缝簇数小于等于4时应力影响范围随着簇数增加,增加较快,当裂缝簇数大于4时增加较慢;垂直于裂缝方向的影响距离要大于平行于裂缝延伸方向的。改变簇间距(30 m)进行了相同的处理方法,得到的曲线与图9和图10基本一致。
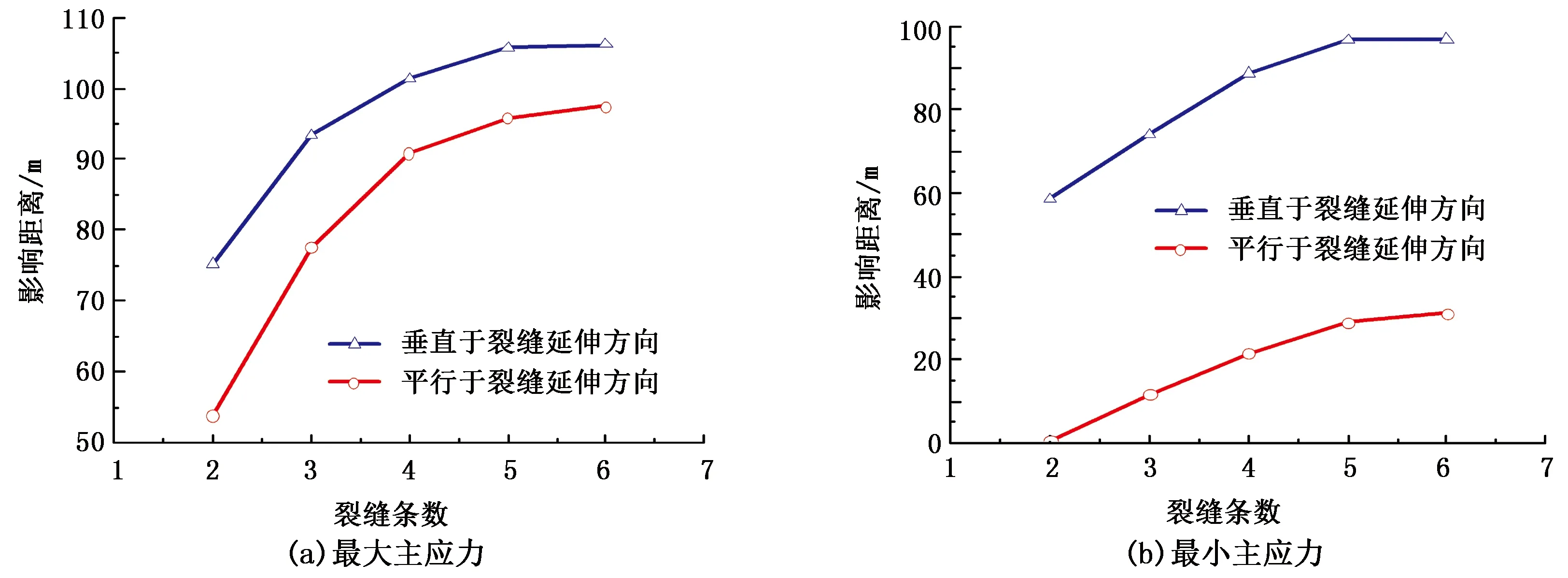
图9 不同压裂簇数下最大和最小主应力影响范围Fig.9 Reach of maximum and minimum principal stresses with different fracturing cluster number
4 不同布缝方式下的应力干扰极限距离
针对油田现场的情况,采取了两种布缝方式(第一种是垂直于裂缝延伸方向,第二种是平行于裂缝延伸方向)见图10。
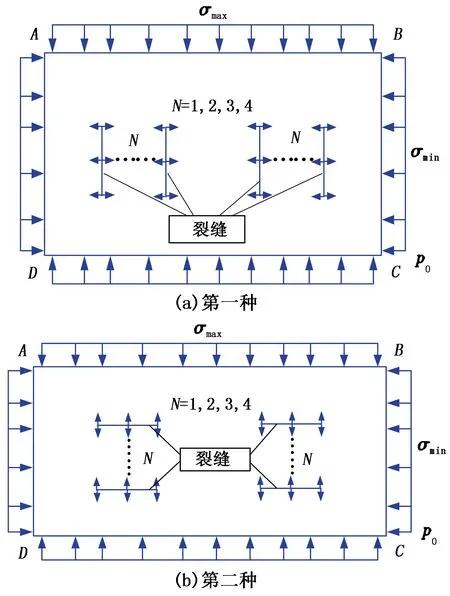
图10 第一种和第二种布缝方式示意图Fig.10 Diagrams under the first and the second decorate fractures
根据图10的布缝方式,分别建立计算模型,将计算结果列于表1、2,表中数据为缝长的倍数。从表中可以看出,每个裂缝群簇数越多应力影响极限距离越长,但增加逐渐放缓;最大主应力要比最小主应力的影响范围大;水平井间距应小于表中给出的极限距离,以利于形成缝网。

表1 第一种布缝方式下不同簇数下缝间应力干扰极限距离Table 1 Seam stress interference limit distance of different clusters under the first decorate fractures

表2 第二种布缝方式下不同簇数下缝间应力干扰极限距离Table 2 Seam stress interference limit distance of different clusters under the second decorate fractures
对比这两种布缝方式的计算结果可以看出,第一种布缝方式应力的影响极限距离明显大于第二种布缝方式下的极限距离,因此在实际生产中建议采用第一种布缝方式,以利于形成缝网。
5 结 论
(1)由于人工裂缝的存在,明显改变了裂缝周围地层应力场分布。采用位移不连续法得到的计算模型可以较好地计算裂缝地层应力分布。
(2)每个裂缝群内簇数越多应力影响距离越长,但增加逐渐放缓,当簇数大于4时,应力影响的极限距离增加速率接近于0。
(3)最大主应力比最小主应力的影响范围大;
簇间距对应力干扰距离基本无影响。
(4)第一种布缝方式的影响极限距离大于第二种布缝方式的,实际生产中建议采用第一种布缝方式,以利于缝网形成。
[1] 王峰,刘长宇,张应安,等.水平井丛书——吉林油田第四分册[M]. 北京:石油工业出版社,2012.
[2] 岳迎春,郭建春.重复压裂转向机制流-固耦合分析[J].岩土力学,2012,33(10):3189-3193.
YUE Yingchun, GUO Jianchun. Fluid-solid coupling analysis of reorientation mechanism of refracturing[J]. Rock and Soil Mechanics,2012,33(10):3189-3193.
[3] 张广清,陈勉,赵艳波.新井定向射孔转向压裂裂缝起裂与延伸机制研究[J].石油学报,2008,29(1):116-119.
ZHANG Guangqing, CHEN Mian, ZHAO Yanbo. Study on initiation and propagation mechanism of fractures in oriented perforation of new wells[J]. Acta Petrolei Sinica, 2008,29(1):116-119.
[4] 陈勉.页岩气储层水力裂缝转向扩展机制[J].中国石油大学学报(自然科学版),2013,37(5):88-94.
CHEN Mian. Re-orientation and propagation of hydraulic fractures in shale gas reservoir[J]. Journal of China University of Petroleum(Edition of Natural Science), 2013,37(5):88-94.
[5] 周健,陈勉,金衍,等.压裂中天然裂缝剪切破坏机制研究[J].岩石力学与工程学报,2008,27(S1):2637-2641.
ZHOU Jian, CHEN Mian, JIN Yan, et al. Mechanism study of shearing slippage damage of natural fracture in hydraulic fracturing[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(S1):2637-2641.
[6] 陈勉,周健,金衍,等.随机裂缝性储层压裂特征实验研究[J].石油学报,2008,29(3):431-434.
CHEN Mian, ZHOU Jian, JIN Yan, et al. Experimental study on fracturing features in naturally fractured reservoir[J]. Acta Petrolei Sinica, 2008,29(3):431-434.
[7] ROUSSEL N P, SHARMA M M. Quantifying transient effects in altered-stress refracturing of vertical wells[J]. SPE Journal, 2010,15(3):770-782.
[8] SIEBRITS E, ELBEL J L, HOOVER R S, et al. Refracture reorientation enhances gas production in Barnett shale tight gas wells[R]. SPE 63030, 2000.
[9] 曲占庆,田雨,李建雄,等.水平井多段分簇压裂裂缝扩展形态数值模拟[J].中国石油大学学报(自然科学版),2017,41(1):102-105.
QU Zhanqing, TIAN Yu, LI Jianxiong, et al. Numerical simulation study on fracture extension and morphology of multi-cluster staged fracturing for horizontal wells[J] Journal of China University of Petroleum(Edition of Natural Science), 2017,41(1):102-105.
[10] 闫相祯,李向阳.基于裂缝干涉模型的非常规油气井压裂优化设计软件的开发与应用[J].中国石油大学学报(自然科学版),2013,37(5):120-128.
YAN Xiangzhen, LI Xiangyang. Development and application of unconventional oil & gas well fracturing optimization design software based on fracture network interference model[J]. Journal of China University of Petroleum(Edition of Natural Science), 2013,37(5):120-128.
[11] 赵金洲,许文俊,李勇明,等.低渗透油气藏水平井分段多簇压裂簇间距优化新方法[J].天然气工业,2016,36(10):63-69.
ZHAO Jinzhou, XU Wenjun, LI Yongming, et al. A new method for cluster spacing optimization of multi-cluster staged fracturing in horizontal wells of low-permeability oil and gas reservoirs[J]. Natural Gas Industry, 2016,36(10):63-69.
[12] CIPOLLA C L, WARPINSKI N R, MAYERHOFER M J. Hydraulic fracture complexity: diagnosis, remediation, and explotation[R]. SPE 115771,2008.
[13] 赵金洲,陈曦宇,刘长宇,等.水平井分段多簇压裂缝间干扰影响分析[J].天然气地球科学,2015,26(3):533-538.
ZHAO Jinzhou, CHEN Xiyu, LIU Changyu, et al. The analysis of crack interaction in multi-stage horizontal fracturing[J]. Natural Gas Geoscience, 2015,26(3):533-538.
[14] CROUCH S L. Solution of plane elasticity problems by the displacement discontinuity method: I infinite body solution[J]. International Journal for Numerical Methods in Engineering, 1976,10(2):301-343.
[15] CROUCH S L, STARFIELD A M, RIZZO F J. Boundary element methods in solid mechanics [M]. George: Allen & Unwin, 1983.
[16] 王飞,董越鹏,黄醒春.弹性层状半平面的位移不连续基本解[J].上海交通大学学报,2009,43(10):1675-1680.
WANG Fei, DONG Yuepeng, HUANG Xingchun. Displacement discontinuity fundamental solutions for a layered elastics half-plane[J].Journal of Shanghai Jiaotong University, 2009,43(10):1675-1680.
[17] OLSON J E, TALEGHANI A D. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures[R]. SPE 163982, 2009.
[18] CHENG Y. Mechanical interaction of multiple fractures--exploring impacts of the selection of the spacing/number of perforation clusters on horizontal shale-gas wells[R]. SPE 125769, 2012.
[19] WU R, KRESS O, WENG X. Modeling of interaction of hydraulic fractures in complex fracture networks[R]. SPE 152052, 2012.
[20] KRESSE O, WENG X, GU H, et al. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations[J]. Rock Mechanics and Rock Engineering, 2013,46(3):555-568.
Criticaldistanceofstressshadowofmultiple-cracksbasedondisplacementdiscontinuitymodel
YAN Xiangzhen1, DONG Wei2, FAN Heng3, YAN Yifei2, XU Jianguo1,4
(1.CAETechnologyResearchCenter,ChinaUniversityofPetroleum,Qingdao266580,China;2.CollegeofMechanicalandElectronicEngineeringinChinaUniversityofPetroleum,Qingdao266580,China;3.CollegeofElectronicEngineering,XianShiyouUniversity,Xian710000,China;4.PetroChinaJilinOilfieldCompany,Songyuan138000,China)
A small specimen test is conducted in MTS to get the elastic modulus and Poissons ratio of tight sandstone core in R13 field. The irregularity of hydraulic crack surface is ignored, and the cracks are simplified as smooth and parallel to each other. Considering the discontinuity of the multi-cracks, they are treated as discontinuous boundaries of the continuous stratum. Then the displacement discontinuity method is used to construct a boundary element model, which is applicable to calculate the distribution of stress around the multi-crack system, and determine the critical distance of the crack swarmsstress shadow with different clusters and different ways of cloth sewn. The results show that the appearance of artificial multiple-cracks has significantly changed the distribution of stress field around the cracks. The more the cluster number, the longer the distance takes effect. But the influence of the cluster number increasing on the distance becomes smaller, taking on a logarithmic tendency. However, the change of crack spacing between 20 and 30 meters, in a single stage has little influence on the critical distance of stress shadow. This study indicates that the boundary element model based on the displacement discontinuity theory can accurately predict the distribution of the stress field around the multiple-cracks and the critical distance of the crack swarmsstress shadow.
multiple-cracks; stress shadow; displacement discontinuity method; critical distance
2017-03-28
国家自然科学基金项目(51374228); 中国博士后科学基金项目(2017M612375);国家科技重大专项(2016ZX05017-003-01);中国石油天然气集团公司重点实验室项目(2016A-3905)
闫相祯(1956-),男,教授,博士生导师,研究方向为油气工程力学。E-mail:yanxzh@163.com。
樊恒(1987-),男,讲师,博士,研究方向为油气工程力学与安全。E-mail:fanheng1@126.com。
1673-5005(2017)06-0140-07
10.3969/j.issn.1673-5005.2017.06.017
TE 357
A
闫相祯,董卫,樊恒,等. 基于位移不连续模型的多裂缝应力干扰极限距离计算[J].中国石油大学学报(自然科学版), 2017,41(6):140-146.
YAN Xiangzhen, DONG Wei, FAN Heng, et al. Critical distance of stress shadow of multiple-cracks based on displacement discontinuity model[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(6):140-146.
(编辑 沈玉英)

