孔板对水槽内流场影响规律

林日亿， 郭 彬, 李晓辰, 徐伟栋, 唐 振

(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.中国石油大学山东省油气储运安全省级重点实验室,山东青岛 266580)

孔板对水槽内流场影响规律

林日亿1,2， 郭 彬1, 李晓辰1, 徐伟栋1, 唐 振1

(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.中国石油大学山东省油气储运安全省级重点实验室,山东青岛 266580)

为了在室内试验台上模拟海洋海流横向冲刷海洋立管，采用水槽内加孔板结构模拟海洋平流。为获取稳定、均匀的平流场，利用FLUENT软件进行水槽内孔板均流流场数值模拟，选用标准κ-ε紊流模型分析孔板孔径、厚度、位置及布置层数等因素对孔板后流场的影响，并优化孔板结构。结果表明：未安装孔板时，在整个水槽内出现射流且有扩散的趋势，但射流并不能带动水槽内全部流体，仅有部分流体有速度，在水槽上、下两端会有漩涡及回流产生，速度分布不均匀。布置3块厚度为0.2 m的孔板且板与板之间的间隔为0.3 m，按照第一块板距离进口截面0.2 m布置且中间孔孔径设计为0.03 m时能够获得较为合理的均匀流场。

孔板; 数值模拟; 计算流体力学; 均匀流场

近年来,对深海石油和天然气的开采与日俱增,海洋立管作为深海石油开采中不可或缺的一个部件,因海流冲刷而设计和建设技术难度大[1]。为研究海洋立管流动规律,试验室内用均流孔板模拟海洋流场,通过水槽研究孔板对流场的影响规律。对于流场的研究,数值模拟相比于实验研究来说具有经济、高效的特点[2],尤其利用计算流体力学(CFD)通用软件后,避免了复杂的编程工作,已成为数值模拟研究流场的有力工具[3]。孔板水流是典型的分离流动,流场高度不均匀,且具有很高的紊动性,分区特性也很明显[4]。在孔口和靠近壁面位置,会伴随有漩涡和回流的出现[5]。朱孟府等[6]和过小玲等[7]选用标准κ-ε湍流模型对孔板的水力特性进行了研究,Yakhot等[8]从理论上导出了κ-ε模型,并用理论分析的方法确定了κ-ε模型中的参数。进行数值模拟时,对标准κ-ε、RNG、RSM三种湍流模型进行比较,表明标准κ-ε湍流模型是更合适的湍流模型[9],Singh等[10]以及Werth等[11]则分别用数值模拟和实验的方法对孔板流量计进行了研究。综上所述,国内外的学者对孔板的研究主要集中在湍流模型的选择、孔板流量计以及孔板的水力特性方面,对孔板的均流作用研究甚少。笔者在室内试验台基础上,通过FLUENT软件开展水槽内孔板均流流场的数值模拟,选用标准κ-ε紊流模型,使用SIMPLEC算法进行计算,分别对孔板孔径、厚度、位置及布置层数等影响因素进行模拟,分析这几种因素对流场的影响,优化孔板结构。

1 物理数学模型

1.1 物理模型

模拟海水平流水槽内充满水,水自左侧口流入,经水槽从右侧口流出(图1)。综合孔板位置、孔径、板数等因素的影响,在水槽内进行孔板布置,最终使流经最后一块孔板后的流场达到均匀。

图1 水槽模型Fig.1 Flume model

计算水槽模型如图1所示,其主要尺寸:长L=5 m,高H=1.3 m,厚δ=0.3 m,进出口直径d=0.2 m,进出口截面为a=0.3 m的正方形截面,顶面长L′=4 m,模型上下左右前后均对称。

1.2 数学模型

1.2.1 控制方程和湍流模型

对于所有的方程,均用FLUENT解质量守恒和动量守恒方程[12],计算控制方程选用连续性方程和动量方程,湍流模型选择标准k-ε双变量湍流模型,因其适用性强,求解稳定,精度也能满足要求。壁面函数的选择保持为标准k-ε湍流模型默认的壁面函数,即标准壁面函数,流动为定常流动,考虑重力。

(1) 质量守恒方程。质量守恒方程又称为连续性方程,其形式为

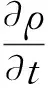
(1)

式中,ρ为流体的密度,kg/m3;ui为流体的速度,m/s。

该方程是质量守恒方程的一般形式,适用于可压缩流动和不可压缩流动。源项Sm是从分散相中加入到连续相的质量, 也可以是任何的自定义源项[13]。

(2) 动量守恒方程。在惯性坐标系下,i方向的动量守恒方程为

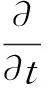
(2)

式中,p为静压力,Pa;τij为应力张量,kg/(m·s2);ρgi和Fi分别为i方向上的重力体积力和外部体积力,kg/(m2·s2)。

Fi包含了其他的模型相关源项,如多孔介质和自定义源项[13]。

1.2.2 控制方程离散

选用SIMPLEC算法进行计算,SIMPLEC算法收敛速度快且计算结果准确,使用Green-Gauss Node Based方法进行迭代,相比于Green-Gauss Cell Based求解更精确且能够最小化伪扩散,压力的离散采用Standard格式,适用性广,其余均采用二阶迎风格式,求解精度高。

2 模 拟

2.1 计算域和计算网格

采用的计算域为如图1所示的水槽模型,计算域网格图以及局部加密图如图2所示。

2.2 边界条件

入口边界为速度入口,大小设置为1.5 m/s,给定湍流强度和水力直径,分别为3.3%和0.2 m,出口边界设为压力出口,出口压力设置为大气压。

2.3 网格独立性检验

以进出口压差为考核依据对网格进行独立性考核,如图3所示。

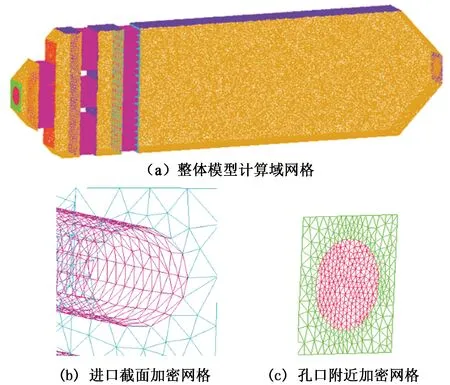
图2 模型网格图Fig.2 Model grid graph

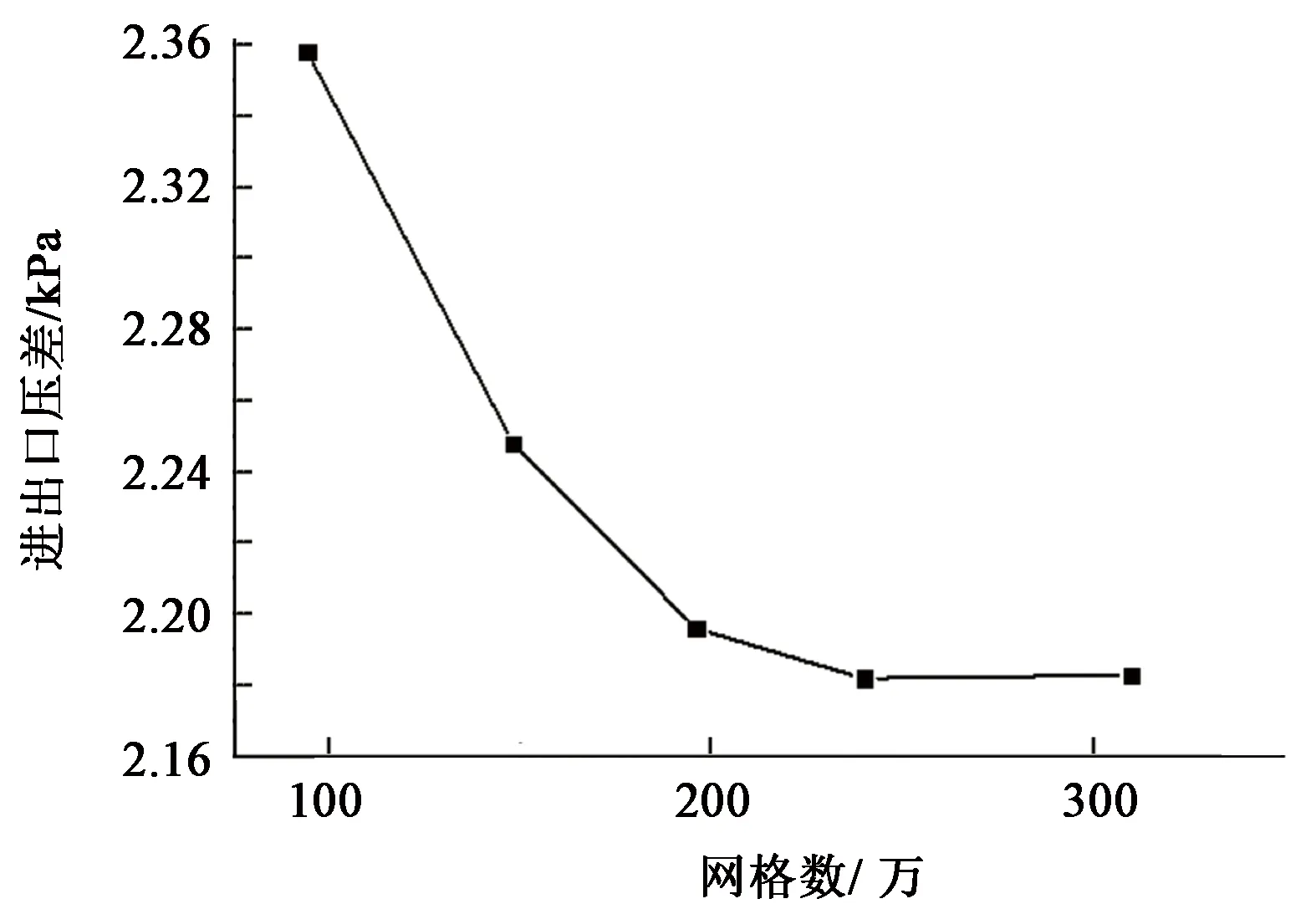
图3 网格独立性考核Fig.3 Grid independence assessment

由图3可以看出,随网格数增加,进出口压差减小;当网格数为240万时,曲线趋于平稳,之后随网格数增加,进出口压差稳定,因此选取240万网格进行计算。

3 结果分析与讨论

3.1 单层孔板时流场的影响因素

3.1.1 位置布置

针对第一块孔板选取3种不同的布置位置,距离入口分别为20、30、40 cm,对应的速度沿高度分布如图4所示。

由图4可以看出,在高度为-1.26 ～-1.0 m内,3种情况均产生回流,且集中在底部,板后回流区产生的位置与文献[14]中结果一致。对比3条曲线,距离进口20 cm时,进口射流扩散范围广,回流速度较其余两种情况小,因此20 cm的情况更优。

3.1.2 孔 径

针对第一块板中间位置孔分别选取3种不同孔径:2、3和4 cm。3种情况下速度沿高度方向分布如图5所示。

由图5可以看出,孔径为2 cm时,水槽两端射流流速大,中间流速小,说明2 cm的孔径较小,射流主要从水槽两端流过;孔径为3 cm时,中间流速大,水槽底部有回流产生,说明在回流区对应位置产生了低压区[15];孔径为4 cm时,速度峰值增大,但峰值较窄,上下两端有回流产生,因此,孔径为3 cm时最优。

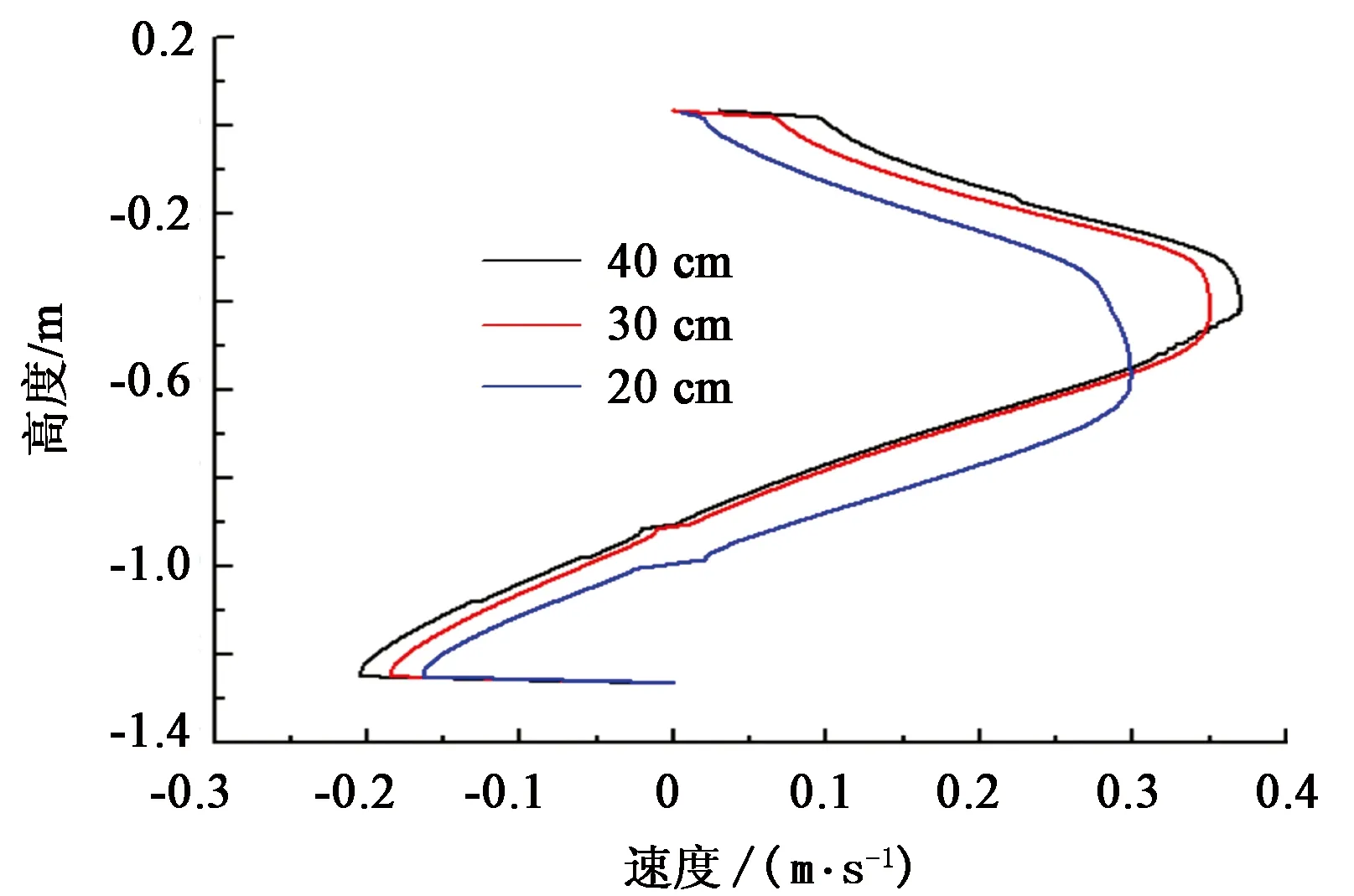
图4 不同布置位置下高度方向速度分布Fig.4 Velocity distribution of height direction under different arrangement positions

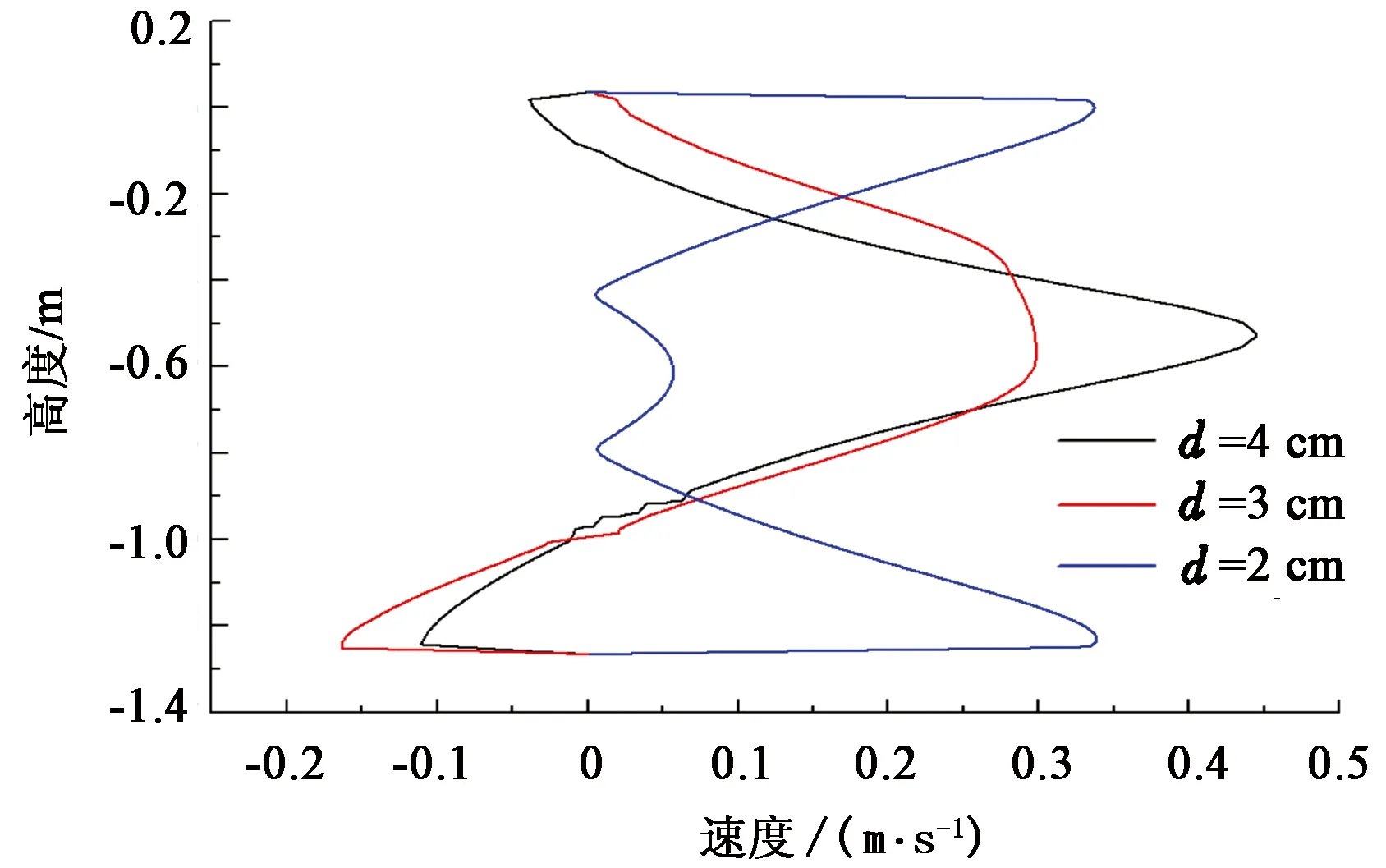
图5 不同孔径下高度方向速度分布Fig.5 Velocity distribution of height direction under different aperture

3.1.3 厚 度

不同厚度时高度方向速度分布如图6所示。

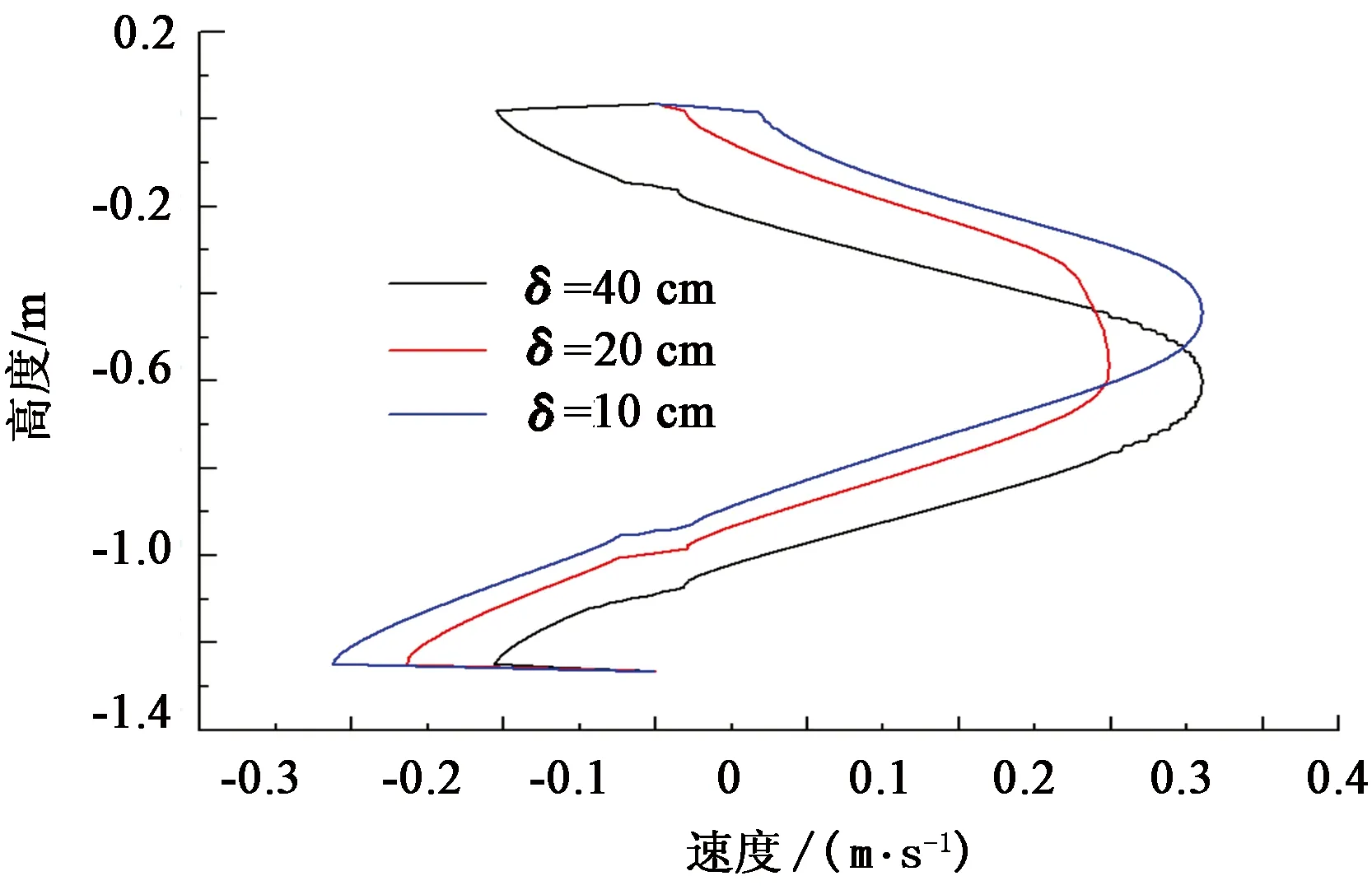
图6 不同厚度时高度方向速度分布Fig.6 Velocity distribution of height direction under different

由图6可以看出,不同厚度间差别较小,底部均产生回流,速度峰值及高度稍有差别,相比来说,厚度为20 cm时回流量小,速度峰值的位置也靠近中间,因此选择厚度为20 cm的孔板。

3.2 多层孔板时流场的影响因素

3.2.1 布置层数

不加孔板和加孔板后的流场分布如图7所示。

由图7可以看出,流场均匀性方面,加入孔板相比于未加入孔板,进口射流得到扩散,随布置层数的增多,进口射流进一步扩散至整个水槽,加人3块孔板后,水槽内流场均匀化。图7(a)中,上下两端流体速度小,接近于零,进口射流在黏性力作用下速度会逐渐减小,在靠近出口处,因出口截面收缩,速度会急剧增大;进口射流速度大,两端速度小,速度不均导致水槽内产生漩涡,进而在上下两端靠近壁面处有回流产生;图7(b)中,加入第一块孔板,核心区自孔口开始,逐渐收缩,主流区内径向流速梯度接近为零,剪切应力也很小[14];加入两层孔板后,射流扩散至整个水槽,仅有个别位置速度较小,回流区消失,符合前述文献研究:随孔板数增加,回流区减少[14]。加入3块孔板后,速度分布均匀化,满足设计要求。

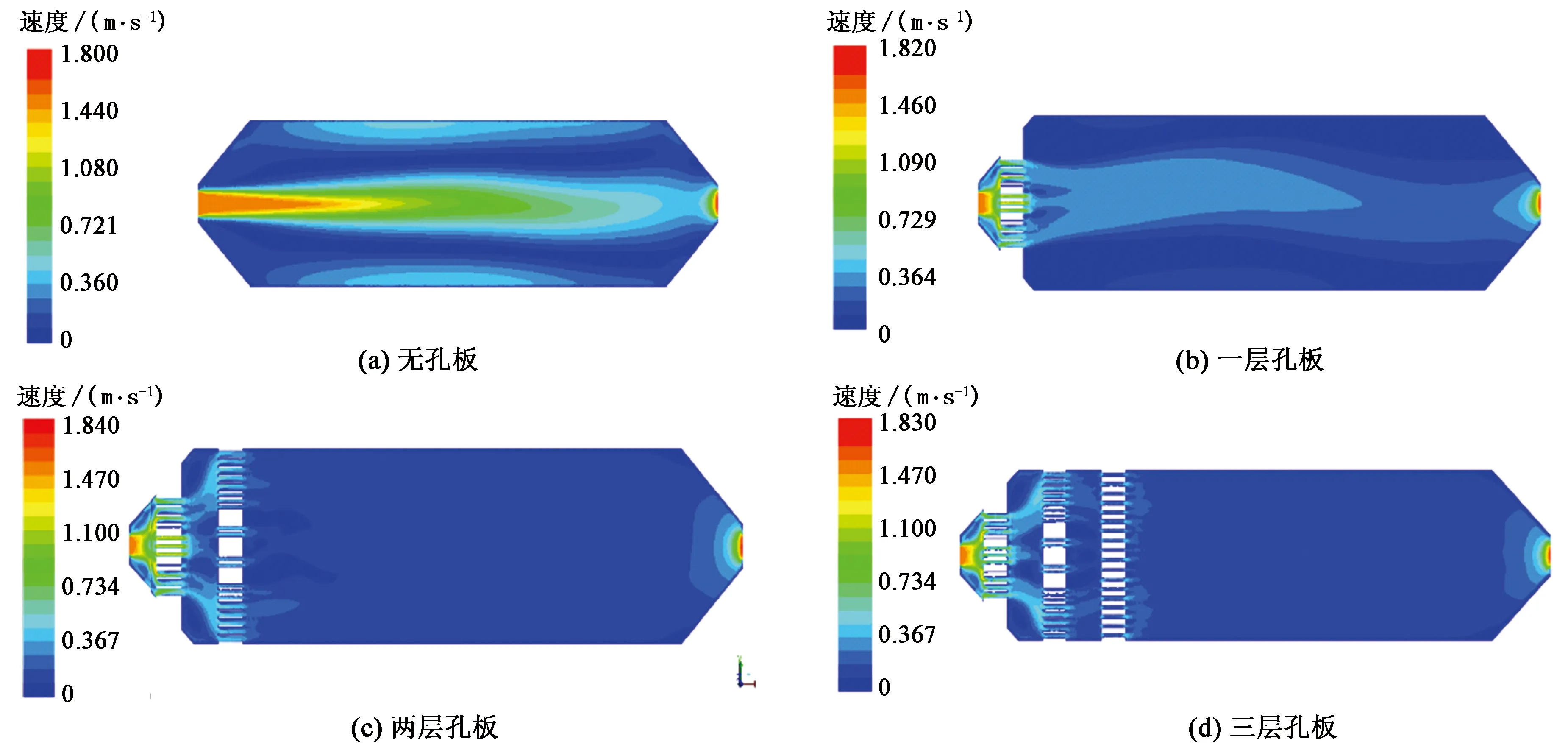
图7 XOY截面速度分布云图Fig.7 Velocity distribution cloud map of XOY section

沿长度方向速度变化曲线如图8所示。由图8可以看出,在接近出口位置,速度均有一个急剧回升。不加孔板时,轴线位置速度大,变化剧烈;加入孔板后,速度变化平稳。加入两块孔板,相较于一块孔板速度更加稳定,但在前期速度会出现波动,综上所述,加入3块孔板是最为理想的布置方式。

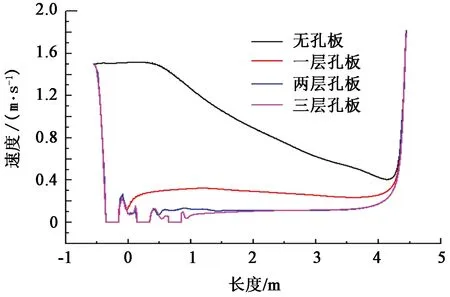
图8 沿长度方向速度变化曲线Fig.8 Curve of velocity along length direction

3.2.2 布置方式

针对第3块孔板选取两种不同的分布方式:顺排和叉排。两种情况下速度分布如图9所示。

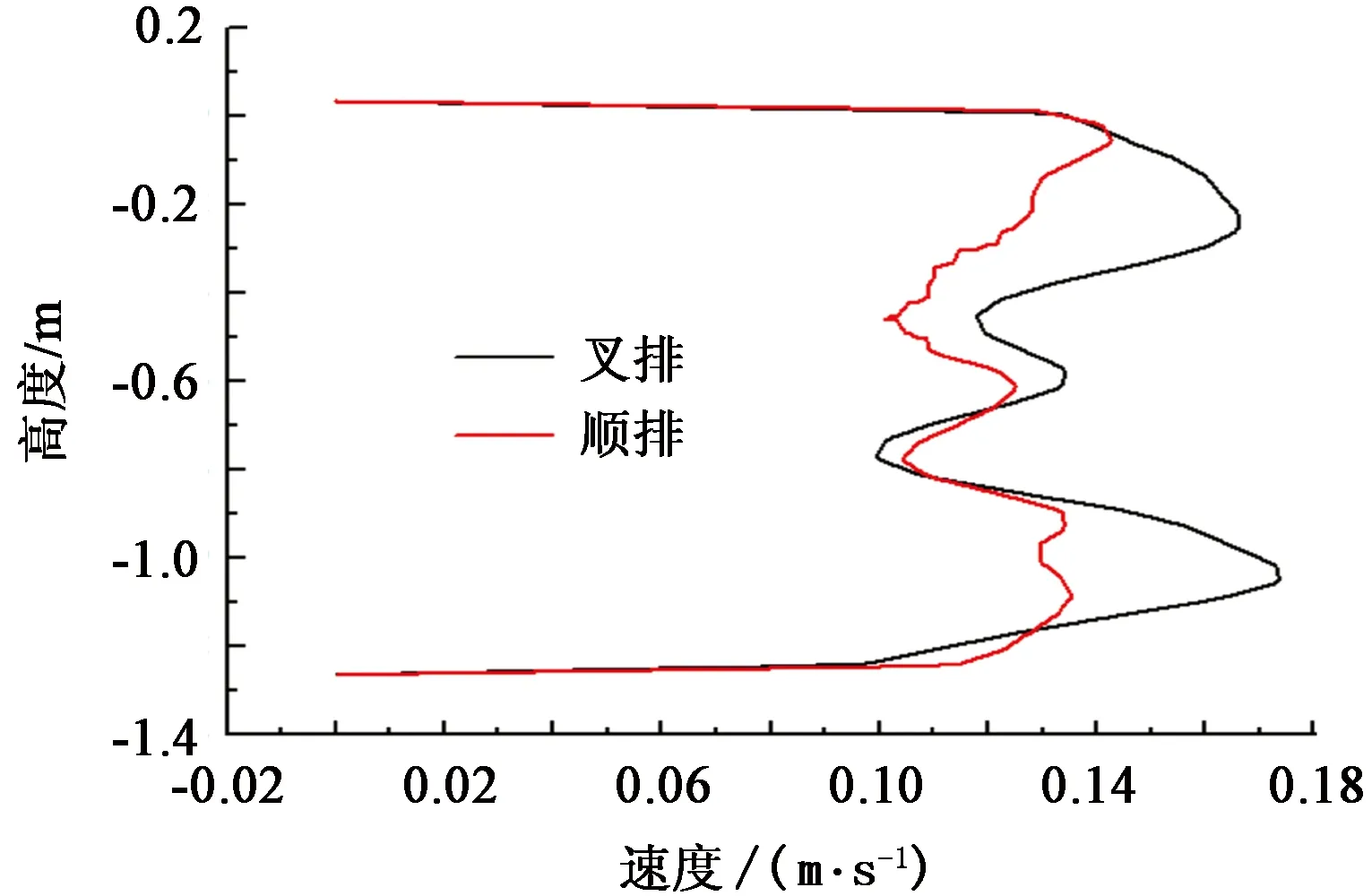
图9 不同分布方式时高度方向速度分布Fig.9 Height direction velocity distribution in different distribution modes

由图9可以看出,两种布置方式下速度沿高度方向均有波动,从波动幅度上来说,顺排布置时,最大速度约为0.14 m/s,最小速度为0.1 m/s;叉排布置时,最大速度约为0.176 m/s,最小速度约为0.098 m/s,因此顺排的布置方式波动幅度相对较小,且从整个高度范围内的速度分布来看,顺排布置下流场更加稳定。

3.2.3 孔眼结构

3块孔板孔眼结构布置如图10所示。由图10可以看出,第一块孔板孔眼分布有两个特点:一是中间分布稀,两端分布密;二是中间孔径小,两端孔径大,目的是将进口射流打散。射流经过第一块孔板后,由图7(b)所示,速度仍集中于中间位置,加入第二块孔板,孔眼结构见图10(b),目的将射流进一步扩散至整个水槽,流向两端。经过两块孔板后的流场如图7(c)所示,仅有个别位置不均匀;为进一步使流场均匀,加入如图10(c)所示的第三块孔板,加入3块孔板后,流场均匀。

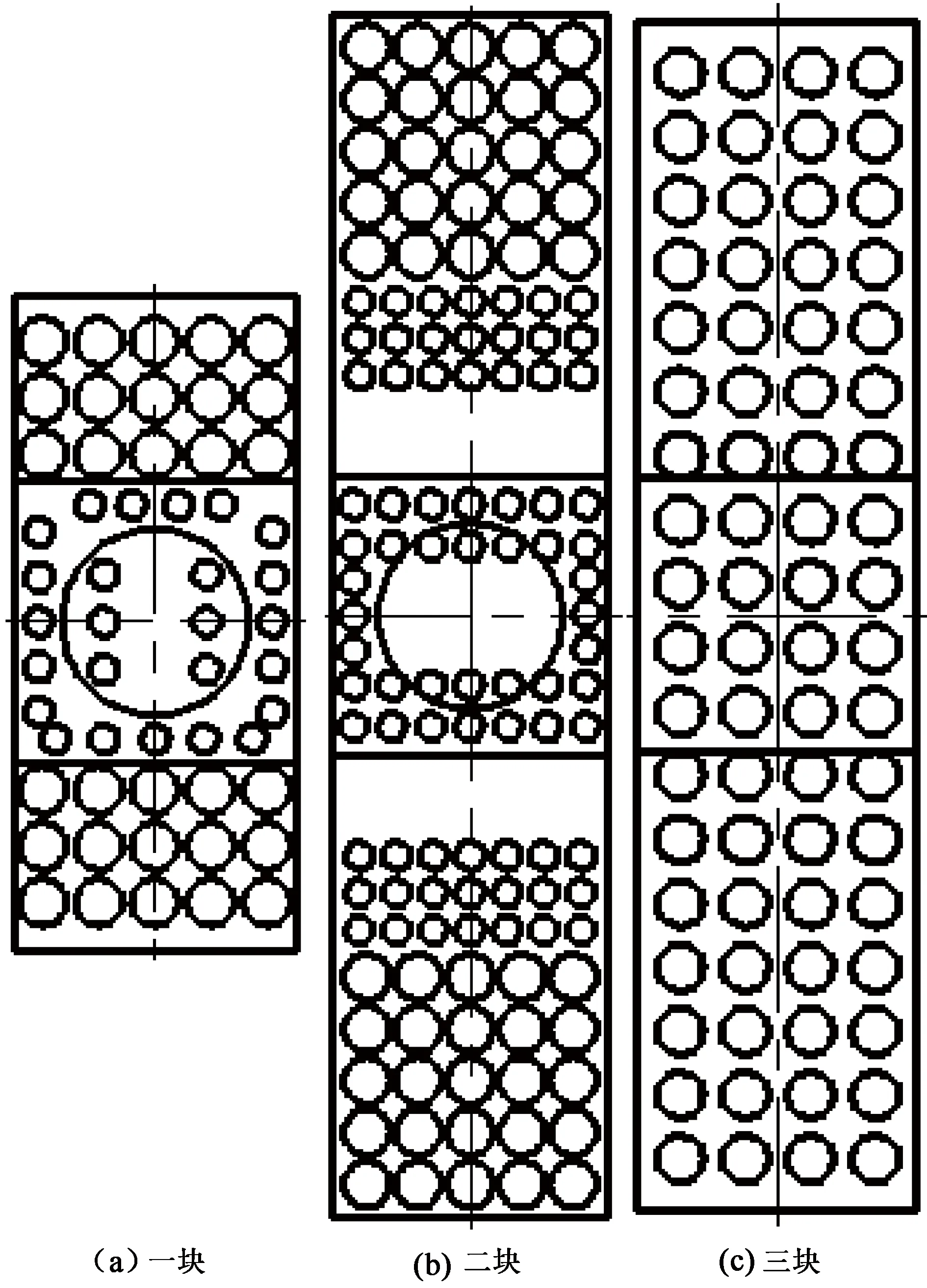
图10 三块孔板孔眼结构布置Fig.10 Three-plate hole structure layout

4 结 论

(1)未安装孔板时,在整个水槽内出现射流且有扩散的趋势,但射流并不能带动水槽内全部流体,仅有部分流体有速度,在水槽上、下两端会有漩涡及回流产生,速度分布不均匀。

(2)相比于位置、厚度等因素,孔径对流场的影响最明显。

(3)孔板结构优化后可实现最佳均匀平流,孔板结构参数为:布置3块间隔0.3 m、厚度为0.2 m的孔板,第一块板距离进口截面0.2 m,前两块板中间孔孔径设置为0.03 m。

[1] DENG Y, HUANG W,ZHAO J. Combined action of uniform flow and oscillating flow around marine riser at low Keulegan-Carpenter number[J]. Ocean University, 2014,13(3):390-396.

[2] SALAH-ADDIN B, AL-OMARI K K, et al. Soot processes in a methane-fueled furnace and their impact on radiation heat transfer to furnace walls [J].International Journal of Heat and Mass Transfer, 2001,44(13):2567-2581.

[3] 于娟.挥发分、CO 火焰与碳粒燃烧的相互作用及其模化[D]. 上海:上海交通大学,2002.

YU Juan. Study and modelling on the interaction of volatile flame,CO flame and char particle combustion[D]. Shanghai:Shanghai Jiaotong University,2002.

[4] 才君梅,马俊,张子冀.孔板流场的二维激光测速试验研究[J]. 水力发电学报, 1999,4:52-58.

CAI Junmei, MA Jun, ZHANG Ziji. An experimental research on the flow field of orifice plate by using the 2-dimension LDV system[J]. Journal of Hydroelectric Engineering,1999,4:52-58.

[5] 杨永刚.方形孔口多孔板水力空化反应器的试验研究与数值模拟[D]. 杭州:浙江工业大学,2012.

YANG Yonggang. Experimental study and numerical simulation of hydrodynamic cavitations reactor with multi-square-hole orifice plates[D]. Hangzhou: Zhejiang University of Technology,2012.

[6] 朱孟府,苗秀娟,邓橙,等.不同孔分布孔板的水力空化效果的数值模拟[J].轻工机械,2012,30(4):8-12.

ZHU Mengfu, MIAO Xiujuan, DENG Cheng, et al. Numerical simulation of hydrodynamic cavitations effect of orifice plate with different layout[J]. Light Industry Machinery,2012,30(4):8-12.

[7] 过小玲,金保升,沈丹,等.装有多孔板的脱硫喷淋塔流场数值模拟研究[J]. 锅炉技术,2007,38(6):5-9.

GUO Xiaoling, JIN Baosheng, SHEN Dan, et al. Flow simulation for FGD spray scrubber with porous plate[J]. Boiler Technology,2007,38(6):5-9.

[8] YAKHOT V, ORZAG S. Renormalization group analysis of turbulence: basic theory[J].Journal of Scientific Computing, 1986,1(1):3-51.

[9] AI W, ZHOU Q J. Hydraulic characteristics of multi-stage orifice plate[J]. Journal of Shanghai Jiaotong University(Science), 2014,19(3):361-366.

[10] SINGH V K, THARAKAN T J. Numerical simulations for multi-hole orifice flow meter [J]. Flow Measurement and Instrumentation, 2015(45):375-383.

[11] WERTH D E, KHAN A A, GREGG W B. Experimental study of wall curvature and bypass flow effects on orifice discharge coefficients [J]. Experiments in Fluids, 2005,39(3):483-489.

[12] 韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M]. 北京:北京理工大学出版社,2004.

[13] 杨肖曦,李松岩,林日亿,等.泡沫流体携砂能力的数值模拟[J]. 中国石油大学学报(自然科学版),2006,30(3):89-96.

YANG Xiaoxi, LI Songyan, LIN Riyi, et al. Numerical simulation for prop-carrying capacity of foam fluid[J]. Journal of China University of Petroleum (Edition of Natural Science),2006,30(3):89-96.

[14] 钟伟.流量测量节流装置的流场数值模拟与实验研究[D]. 南京:南京航空航天大学, 2007.

ZHONG Wei. Numerical simulation and experimental study on measuring the flow field of throttling device[D]. Nanjing:Nanjing University of Aeronautics & Astronautics, 2007.

[15] 郭婷婷,李雪梅,格日勒,等.电站挡风抑尘板后流场特性的数值研究[J].电站系统工程,2009,25(2):7-10.

GUO Tingting, LI Xuemei, GE Rile, et al. Numerical simulation on flow characteristics of porous wind fences[J].Power System Engineering,2009,25(2):7-10.

Influencelawsofporeplatesonbasininternalflowfield

LIN Riyi1,2, GUO Bin1, LI Xiaochen1, XU Weidong1, TANG Zhen1

(1.CollegeofPipeline&CivilEngineeringinChinaUniversityofPetroleum,Qingdao266580,China;2.ShandongProvincialKeyLaboratoryofOil&GasStorageandTransportationSafety,ChinaUniversityofPetroleum,Qingdao266580,China)

In order to simulate the situation how the vertical tube is washed by the seawater inside the tube, this study is aimed to simulate the ocean advection by using the pore plate structure in a flume.To obtain the stable and uniform velocity field, the FLUENT software is used to simulate the stable velocity field by using the pore plate structure in a flume. The standardκ-εturbulent model is adopted to analyze the pore diameter, thickness, position and arrangement layers of the pore plate, then the structure of the pore plate is optimized. The simulation results show that, when the orifice plate is not installed, there is a trend of jet and diffusion in the whole tank, but the jet does not drive all the fluid in the tank. Only part of the fluid has the velocity, in the water tank, the lower end has whirlpool and reflux generation, and the velocity distribution is not uniform. It is more favorable to obtain the uniform flow field with three pore plates whose thickness is 0.2 m, where the interval between them is 0.3 m,the first pore plate is set to 0.2 m away from the inlet, and the diameter of the hole on the first pore plate is set to 0.03 m.

pore plate; numerical simulation; computational fluid mechanics; uniform flow field

2016-09-30

“十三五”国家科技重大专项(2016ZX05012-002-005);中央高校基本科研业务费专项(15CX05002A)

林日亿(1973-),男，教授,博士,研究方向为热力采油和热能利用。E-mail:linry@upc.edu.cn。

1673-5005(2017)06-0154-06

10.3969/j.issn.1673-5005.2017.06.019

TE 952

A

林日亿,郭彬,李晓辰,等. 孔板对水槽内流场影响规律[J]. 中国石油大学学报(自然科学版), 2017,41(6):154-159.

LIN Riyi, GUO Bin, LI Xiaochen, et al. Influence laws of pore plates on basin internal flow field [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(6):154-159.

(编辑 沈玉英)