一种基于邻域作用力的三维网格平滑方法
王海起, 彭佳琦, 王 艺, 董倩楠, 车 磊, 龚蔚青
(1.中国石油大学地球科学与技术学院,山东青岛 266580; 2.中国石化石油勘探开发研究院,北京 100083)
一种基于邻域作用力的三维网格平滑方法
王海起1, 彭佳琦1, 王 艺1, 董倩楠1, 车 磊1, 龚蔚青2
(1.中国石油大学地球科学与技术学院,山东青岛 266580; 2.中国石化石油勘探开发研究院,北京 100083)
针对以不规则六面体为基元的三维网格模型在对三维区域边界表达时存在锯齿现象,在保持原有网格拓扑结构不变的情况下,提出一种基于离散属性数据的邻域网格相互作用力平滑方法。受磁铁“同性相斥”物理特性的启发,将三维网格模型共用顶点的邻域网格体元素根据属性值划分为不同的体块,体块之间具有相斥的作用力,根据体块对顶点的作用合力方向和大小确定网格顶点平滑移动的方向和距离。实际应用表明平滑存在着“拐点”现象,平滑系数取值接近拐点时平滑效果较好,取值偏大或偏小评价指标性能下降。
六面体网格; 锯齿效应; 三维平滑; 邻域网格; 作用力
真三维地质体建模的模型体元通常采用六面体、四面体、棱柱体等[1],其中,六面体网格具有组织形式规则、网格单元数量及重划分次数较少、计算效率高等优点,在三维地质体、油藏体建模中应用广泛,并被大多数商业油藏建模和数值模拟软件所支持[2-4]。然而,这种源自矩形网格的体模型在对三维区域边界进行离散化网格表达时存在锯齿效应。高精度的精细地质模型可以降低锯齿效应的影响、提高表征精度,但即使对于一个中等规模的油藏体,精细的地质表征往往具有百万级甚至千万级的网格规模,受限于实际实现技术,精细地质模型和油藏数值模拟器可以支持的网格规模之间存在着较大差距,对三维网格进行粗化就是将精细地质模型粗化到油藏数值模拟器能够接受的网格规模[5]。然而粗化后的网格六面体体元较大,对圈闭、油层等区域边界的表达由于锯齿效应的存在不符合实际的地质现象,影响模型的描述精度、可视化效果及后期模拟计算的准确性。对于六面体模型边界锯齿现象,可以采用边界网格重构或加密方法解决[6],这种方式可以构造出精细的边缘形状,达到了精细的平滑效果,但对于油藏模型组织结构来说,这种方法打乱了原有结构的规则行列网格检索方式,为查找和数值模拟计算增加了难度。另一种解决途径通过适当移动六面体的顶点进行平滑,这种方式只能进行粗略的平滑,难以刻画精细的边缘形状,但保留了原有的网格组织形式,网格数和顶点数均没有发生改变。针对锯齿平滑问题,笔者提出一种邻域网格作用力平滑算法,考虑到实际应用中油藏模型并不需要特别精细地刻画边缘,同时要保持网格原有的三维拓扑结构,平滑采用网格顶点位置自适应优化方式,根据不同属性值体块之间的相互作用力,确定顶点平滑移动的方向和距离。
1 三维平滑算法
对于网格平滑,经典的平滑算法包括Laplacian平滑、Taubin平滑、平均曲率法等。Laplacian平滑的核心是将网格内部节点的位置移动到与该节点共面节点组成的多面体的体心处,算法简单[7]。Taubin算法在Laplacian算法的基础上引入了滤波器及权系数,可抑制拉普拉斯算子引起的变形收缩[8]。平均曲率法则遵循曲面曲率变化均匀即为光滑的原则[9]。上述方法各有优缺点[9],不少学者亦在此基础上进行了大量的优化改进,但是对于三维油藏网格模型,这些平滑方法在应用时会产生一些问题。
三维油藏网格模型不同于其他建筑或工具的三维模型。图1所示为某工程零件的三维六面体网格模型,这类模型所有网格属性相同,只需对表面因形状产生的锯齿进行平滑。油藏网格模型表面并不需要平滑,模型内部因为网格属性值不同产生的锯齿现象需要平滑,若分别将相同属性值的网格提取出来对表面进行平滑,平滑后的拓扑关系可能被破坏。
综上,如何能借助六面体网格模型三维点阵的查找优势,避免破坏原有的网格结构,又能保证网格之间的三维拓扑关系,是三维油藏模型平滑的关键问题。
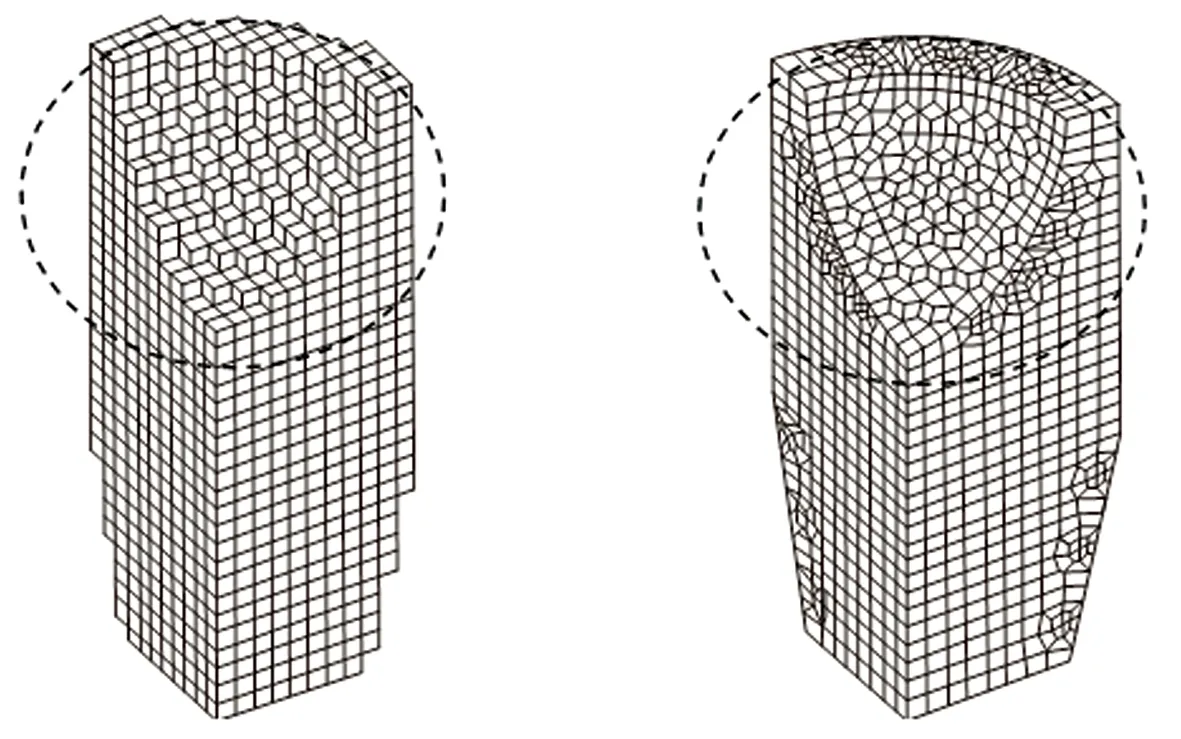
图1 六面体网格边界重构加密Fig.1 Boundary reconstruction and densification of hexahedral meshes
2 邻域网格作用力平滑算法
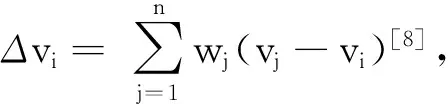
在三维网格平滑中,对上述平滑思路进行扩展,以顶点周围共用该顶点的8个邻域网格体组成平滑窗口,将网格体划分为不同的体块,不同体块对顶点相斥作用力的大小度量了顶点平滑移动的不同权重,所有体块作用力的合力决定了顶点最终移动的距离和方向。
以图2为例阐述算法的主要思路,设顶点v周围8个网格体的离散属性值代表不同的沉积微相类型,如用1、2、3分别代表坝主体、坝缘、前三角洲类型,相同的属性值指示相同的沉积微相类型,据此可将8个邻域网格体划分为3个体块B1、B2、B3,分别代表上述3种微相类型。为了便于展示,图2中将顶点v与邻域网格单元拉开了距离。
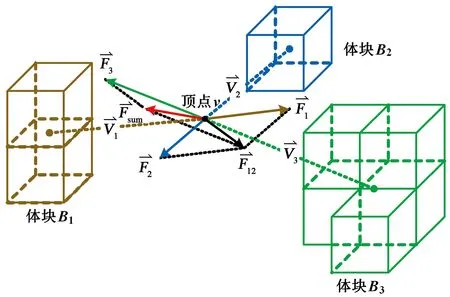
图2 邻域作用力示意图Fig.2 Schematic of neighborhood forces
将每个体块看作磁铁的“同极”,各同极对顶点v具有相斥的作用力,作用力采用基于重力模型改进的空间相互作用力SIM模型(spatial interaction model)进行度量[10-11]。设体块Bk的质量为Mk,顶点v质量为Mv,体块Bk对顶点v的相斥作用力向量Fk大小为
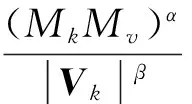
(1)
式中,G、α分别为引力常数和质量指数,这里可取1;Vk为体块Bk中心与顶点v连线向量,体块中心可取几何中心或质心,|Vk|为向量模,表示体块Bk与顶点v的距离;β为距离指数,亦可取1。
Fk方向由Vk确定,图2中3个体块对顶点v的作用力F1、F2、F3大小分别由式(1)确定,方向分别由向量V1、V2、V3确定,则合力Fsum实际上是3个作用力向量之和。
对于每个Fk,取G=α=β=1,由运动定律F=ma可知顶点v的加速度向量ak大小为
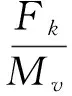
(2)
ak方向同样由Vk确定。借鉴万有引力搜索算法GSA(gravitational search algorithm)的处理方式[12],在不考虑初始速度和时间的前提下,加速度ak代表了顶点v在作用力Fk作用下的移动偏移量Δdk,则在合力Fsum作用下总的移动偏移量为各向量Δdk之和。
上述公式亦说明Δdk大小与体块Bk的质量Mk成正比,与距离|Vk|成反比。将每个网格单元的质量简单地视为1,则Δdk大小实际上与体块Bk包含的网格单元个数nk成正比,表明当体块包含的网格单元较多时,对顶点的作用力较大,顶点移动距离较长,如图2中的体块B3;反之,则对顶点的作用力较小,顶点移动距离较短,如体块B2。
对三维区域边界的锯齿进行平滑处理,目的是降低边界表达的噪声,使其符合实际的地质现象。对于有些顶点,例如断层、尖灭等,是不需要进行平滑处理的。当顶点需进行平滑处理时,其邻域的各体块总是将顶点外推,目的是使体块尖锐、锯齿状的边界面和边界点趋向光滑,这与地层分界面的连续性是一致的,只不过质量较大的体块将顶点外推的作用力较大,质量较小的体块将顶点外推的作用力较小,不同方向、大小的作用力形成合力最终将顶点推到相对平衡的位置,既降低了边界的锯齿效应,又保持了网格的稳定性。
综上,算法的主要思路可概括为:将共用同一顶点的8个邻域网格体划分为不同的体块,每个体块包含具有相同属性类型的网格。将每个体块看作磁铁的“同极”,同极之间具有相斥的作用力,顶点移动的方向为体块作用力的方向,移动的距离以作用力的大小作为权重,作用力大则移动距离大,作用力小则移动距离小。所有体块合力的方向和大小决定了顶点最终移动的方向和距离。
通过该方法以顶点邻域八网格体为平滑窗口,依次遍历各顶点,若某顶点邻域八网格体具有相同属性值,则认为该顶点邻域区域具有均质性,不需要平滑。
下面对网格体块分布的几种具体情况进行图示分析:
(1)顶点邻域八网格存在两种不同属性值,如图3(a)所示,黄色网格个数为1,绿色网格个数为7,左图为原始结构,中图黄绿箭头为两种力的作用方向,红色箭头为合力的作用方向,右图为顶点沿合力方向平移后的效果。
(2)顶点邻域八网格存在4个黄色网格和4个绿色网格,如图3(b)所示,上下两侧的作用力相互抵消,不需要平滑。
(3)顶点邻域八网格存在3种不同属性值,作用力效果与平滑效果如图3(c)所示。
(4)如图3(d)所示的5×5网格中心存在一凸起网格,左图红色箭头示意各顶点的移动方向,右图为顶点移动平滑后的效果。
(5)在剖面情况下,图4左图为处理前的网格,红色箭头示意相应顶点移动的方向,右图为顶点移动后的网格,可以看出,该方法同样也适用于二维网格的平滑。
对于共用顶点的八网格,若体块包含的网格数较少,例如只有1个网格,如图3(a)所示的黄色网格,则意味着该网格是孤立的,是一个凸起,需要平滑凸起边界;反过来看,绿色网格的数量较多,可以看作成包围趋势,则意味着绿色网格存在一个凹陷,需要平滑凹陷边界。在本文提出的算法中,借助“同性相斥”的作用力思想,给网格数量较多的体块一个较大的力,给网格数量较少的体块一个较小的力,从而合力的方向和大小决定了顶点移动的方向和距离,这种方法的结果也符合前述的平滑规律。
对于具有更多属性值的网格、或者属性值交错散乱分布的情况,如图5所示,每个网格几乎都相当于一个异变(凸起或凹陷),这种情况一般不需要进行平滑处理,应保持其原有的特征。对应到本文的方法,若属性分布散乱,则会产生四面八方的力,这些力互相抵消或完全抵消,则顶点仅需做细微的移动、或不移动,因此在复杂情况下,本文的方法也符合一般的平滑规律。实际上,在油藏模型中,地质属性的分布是有一定规律的,属性在一个顶点周围散乱分布的情况较为少见。
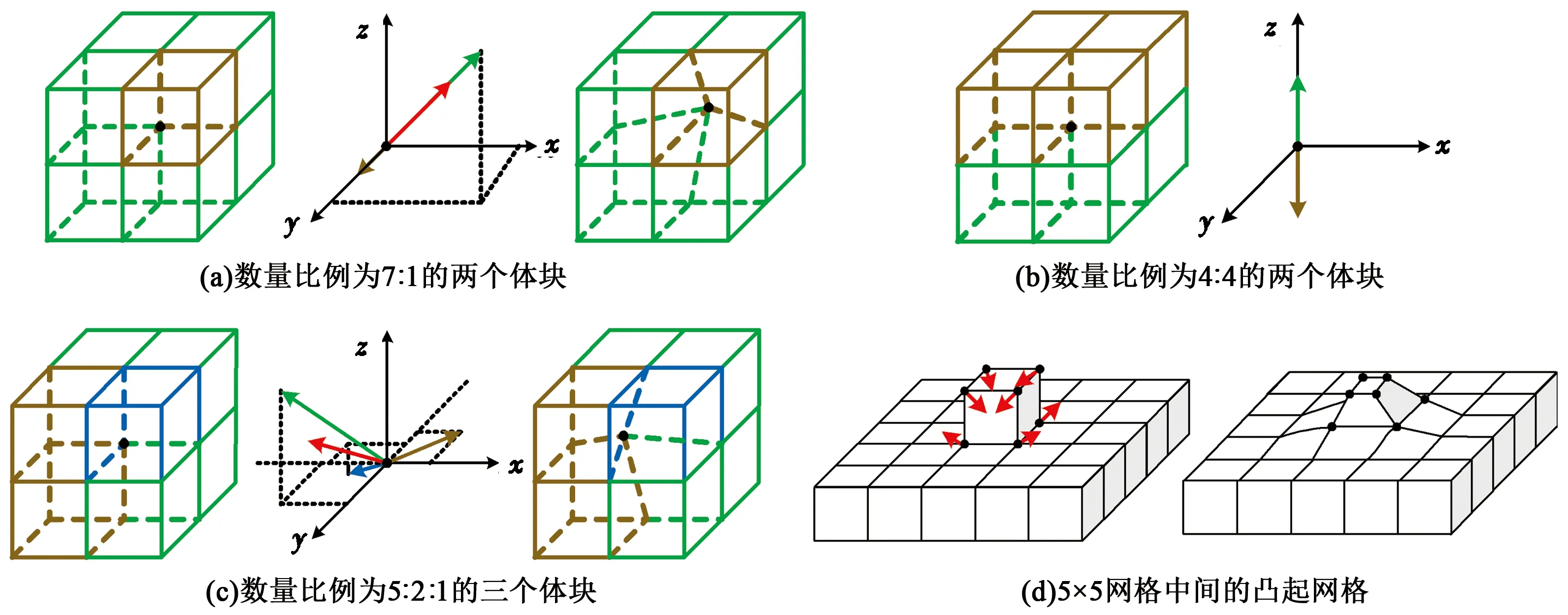
图3 不同体块的作用力平滑Fig.3 Smoothing based on forces of different blocks
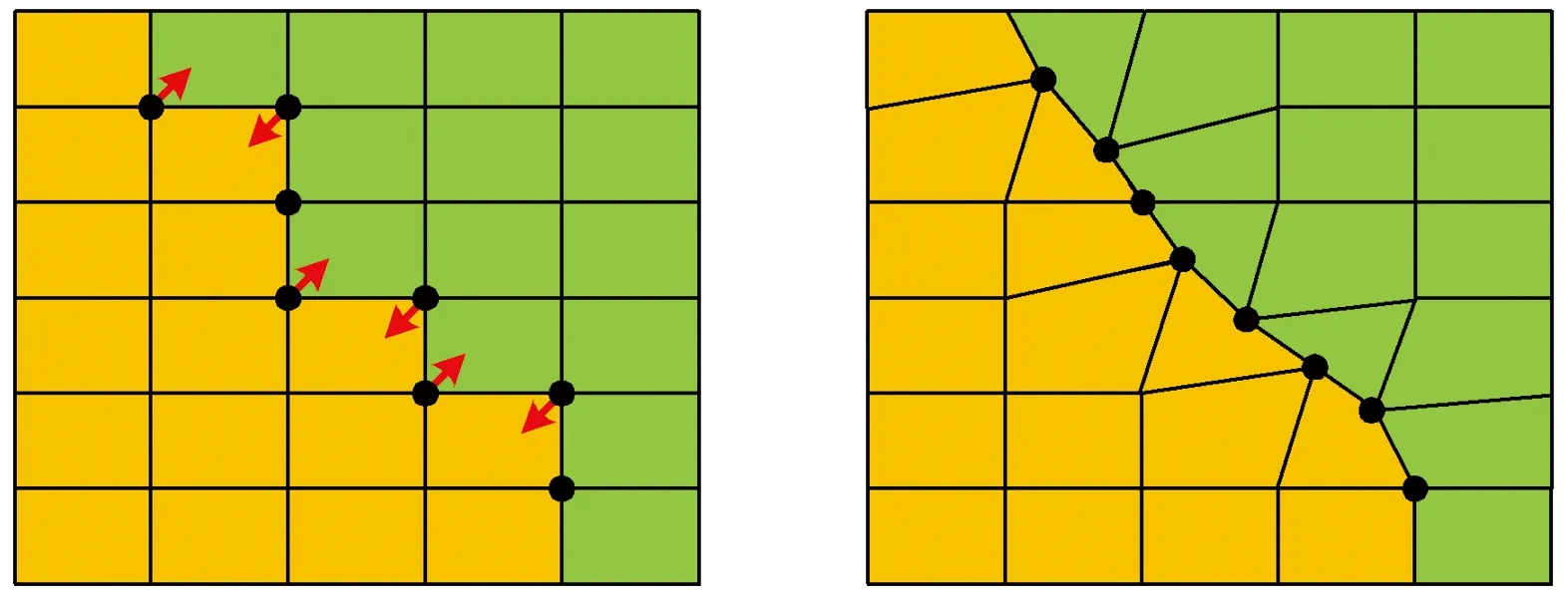
图4 剖面情况下两种属性的平滑效果Fig.4 Smoothing effect of two attributes in a profile view
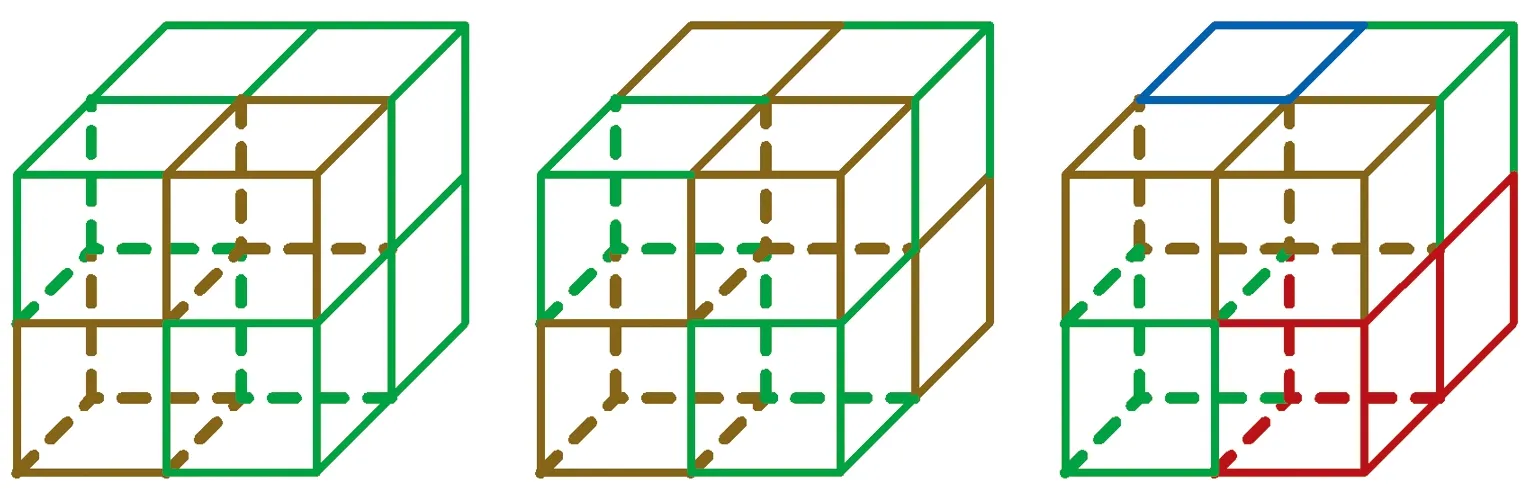
图5 邻域网格的其他体块分布情况Fig.5 Distributions of other blocks for eight-neighbor meshes
3 平滑算法流程
在油藏模型中,有些不需要平滑的特殊点,如图6的示意图中,模型边界的角点、边点不需要进行平滑;带有断层特征的点不需要进行平滑;另外一些具有特殊意义的特征点,例如特殊底层的尖灭,应在平滑处理前由地质工程师进行交互操作,圈定或输入一些特征点或特征区域,避免平滑时被破坏。遍历网格逻辑IJK顶点时,判断其是否为特征点,若不是特征点,则进行平滑处理。
平滑算法的具体流程如下:
(1)根据网格IJK集合及顶点索引集合依次遍历三维模型每个顶点,及共用该顶点的邻域网格;对于每个顶点,进行下面(2)~(9)步处理。
(2)设遍历的当前顶点v坐标为(xv,yv,zv),则①若顶点为边界面上的点,统计顶点邻域网格在边界面上的属性值分布情况,若属性值不相同,在二维面上采用(3)~(9)步进行顶点移动平滑;②若顶点为三维模型的角点或边点,则不进行平滑处理;③若顶点为被标注过的特征点,则不进行平滑处理;④若顶点在模型内部,且邻域网格属性值均相同(无效网格亦被看作一种网格属性值),则认为是均质的,不需要处理;⑤若顶点在模型内部,且邻域网格属性值不相同,则进行(3)~(9)步处理。
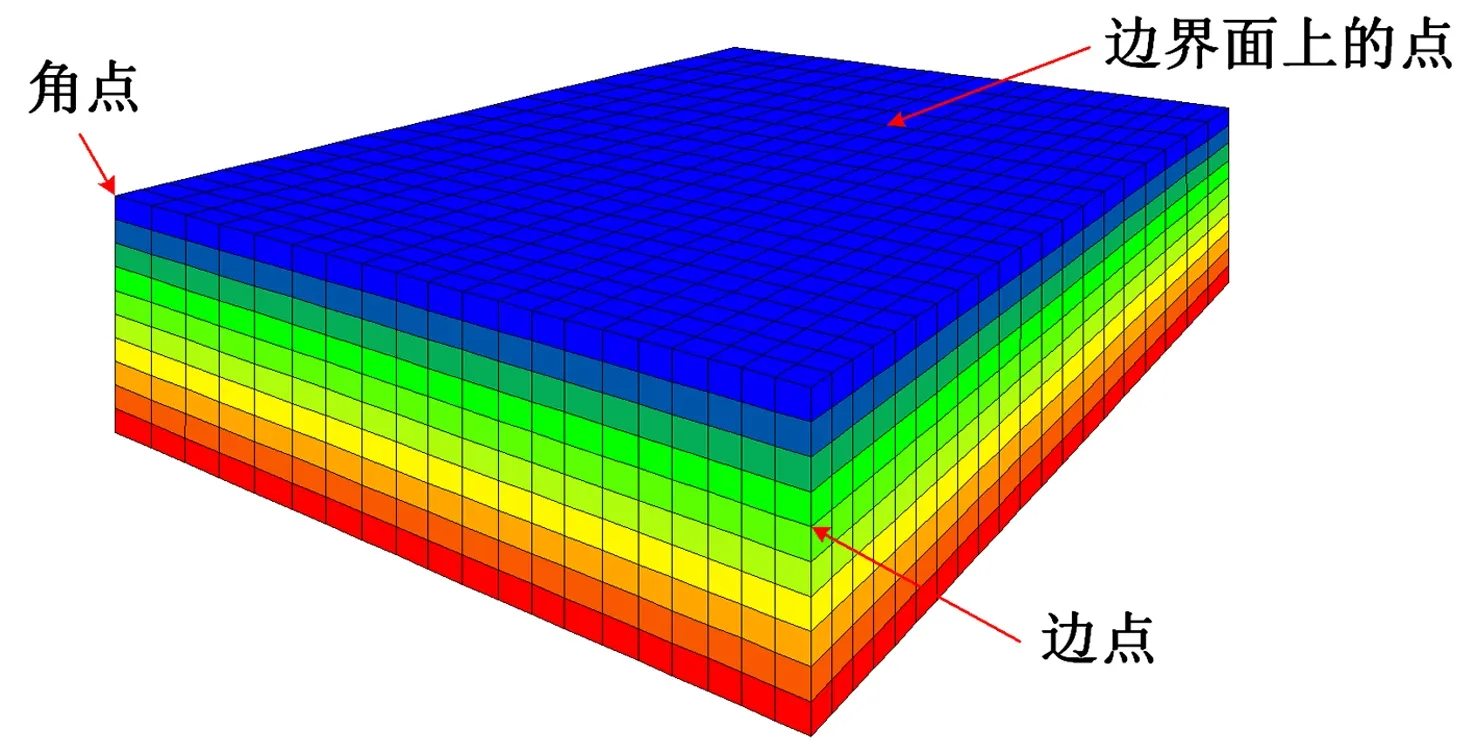
图6 三维模型表面顶点不同位置分布示意图Fig.6 Distribution schematic of different positions of surface vertexes of 3D model
(3)计算当前顶点各邻域网格质心坐标。将每个六面体邻域网格单元视为均质,设网格单元各顶点的坐标为(xi,yi,zi),其中i=1,2,…,8,i为顶点序号,网格单元质心坐标为(xc,yc,zc),质心计算公式为
(3)
(4)计算体块质心坐标。将属性值相同(将无效网格看作同一类属性值)的邻域网格看作一个体块,则顶点(xv,yv,zv)的8个邻域网格单元可分为多个体块{Bk}。
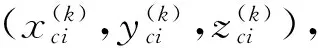
(4)
(5)计算体块Bk对当前顶点作用力的方向向量。利用体块质心与当前顶点(xv,yv,zv)的连线确定方向向量Vk,计算公式为
Vk=(Xk-xv,Yk-yv,Zk-zv).
(5)
(6)计算体块Bk对当前顶点作用力的移动距离。将体块Bk包含的每个网格单元质量视为1,体块质量即为体块包含的网格单元个数nk。体块质量大,则对顶点的作用力大,顶点移动距离长;反之,则作用力小,顶点移动距离短。
对于六面体模型,任一顶点(xv,yv,zv)的邻域网格单元个数最多为8个,当所有邻域网格均属于同一个体块时,则意味着邻域网格属性值均相同,邻域网格单元是均质的,顶点不需要进行平滑处理,即前述第(2)步中④ 说明的情况,因此体块Bk的最大质量为7,则nk/7可以作为相对于最大质量作用的最长移动距离,体块质量为nk时的移动距离权重。设六面体网格对角线长度Ldiag为顶点移动距离的上限,则顶点(xv,yv,zv)在体块Bk作用下的移动距离Δdk(Δdk为移动偏移向量Δdk的数值)可表达为
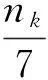
(6)
式中,γ为平滑系数,用于对最大移动距离进行约束。
(7)根据体块Bk的方向向量Vk、移动距离Δdk,则在体块Bk作用下顶点(xv,yv,zv)的移动距离向量为
(7)
其中
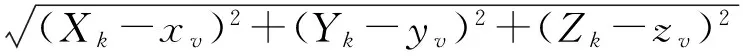
(8)所有体块{Bk}合力作用下的移动分量为
(8)
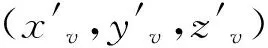
(9)
算法流程如图7所示。
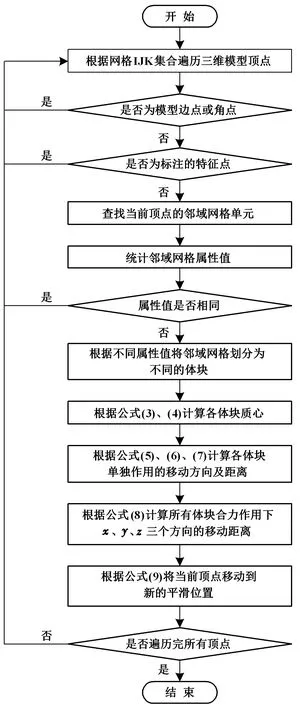
图7 平滑算法流程Fig.7 Flow chart of smoothing algorithm
4 算法分析及应用
4.1 平滑系数γ分析
当邻域网格划分为体块后,公式(8)中每个体块的质心位置(Xk,Yk,Zk)、方向向量Vk、包含的网格个数nk及网格对角线长度Ldiag都是确定的,因此平滑系数γ的选择对平滑效果至关重要。
对于三维地质体平滑,当遇到“凸起”或“凹陷”时,需要对其平滑,而不是将其完全“削掉”或“填平”,故对顶点移动时,应小于网格对角线长度的一半。直观上理解,如图8所示的二维规则网格,当移动距离约为对角线长度的1/4时,恰好将斜边平滑近似为一条直线,较为符合常理。
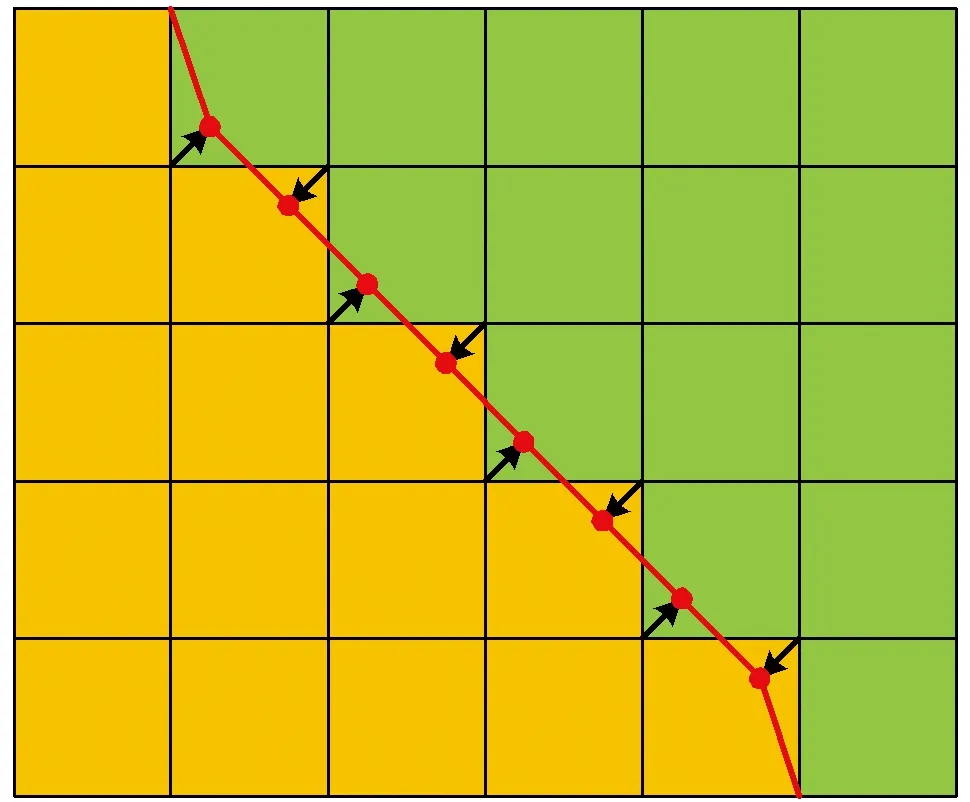
图8 两种属性交界的斜边平滑Fig.8 Hypotenuse smoothing of borderlines of two attributes
为了确定最佳平滑系数,对γ不同取值的平滑结果进行比较,评价指标为平滑顶点与体块分界面上所有相邻顶点连线形成的夹角余弦值的平均值。
图9为二维视角下两个邻域体块分界线上的平滑顶点与处于分界线上的相邻顶点形成的向量夹角及相应的余弦值。
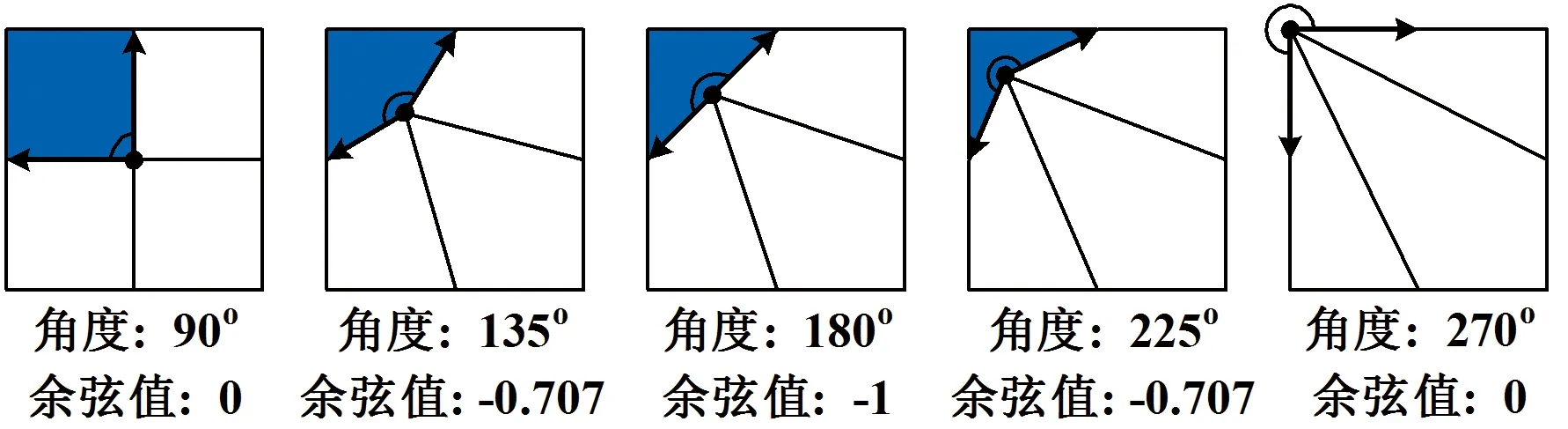
图9 不同夹角对应的余弦值Fig.9 Different angle and its cosine
从图中可以看出,两向量夹角越接近于180°,即夹角连线越接近于直线,余弦值越接近于-1,平滑效果越好。
三维视角下,对于分界面上的平滑顶点,需要分别计算与XOY、XOZ、YOZ三个剖面上处于分界线上的相邻顶点连线形成的向量夹角余弦值,取其平均值作为评价指标评价整体的平滑效果,其值越接近于-1,平滑效果越好。
采用的测试网格为二维规则格网,网格划分为63×63,网格大小为1 m×1 m×1 m,平滑系数γ不同取值的平滑效果及评价指标变化情况分别如图10、图11所示。
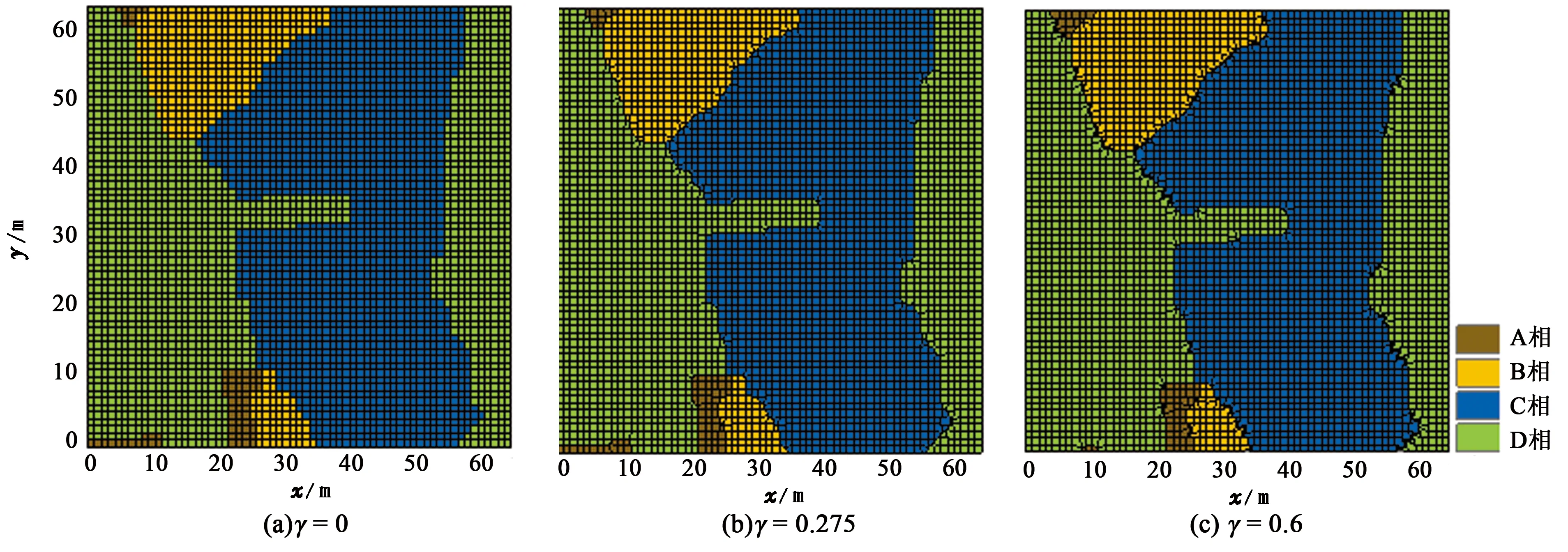
图10 不同平滑系数γ的平滑效果Fig.10 Smoothing effect of different smoothing factor γ
分析平滑效果及变化曲线图,平滑系数γ为0表示没有进行平滑,如图10(a)所示;随着γ值逐渐增大,平滑发生作用,评价指标也趋向-1;当平滑系数γ增大到某个值(本算例为0.275)时,曲线到达拐点位置,评价指标达到最为接近-1的值(本算例为-0.3013),此时平滑效果最好,如图10(b)所示;之后,随着γ取值继续增大,平滑性能下降,从图10(c)可以看出,边界出现过度平滑现象。
对规则六面体格网,采用其他算例进行相同的计算,最佳平滑系数(曲线拐点位置)变化不大,γ基本在0.26~0.29变化。对比实际图形可发现,当区域边界出现较多的连续台阶状锯齿现象时,如图12(a)所示,拐点位置更接近于γ=0.26;当区域边界出现较多的直角转弯现象时,如图12(b)所示,拐点位置更接近于γ=0.29。实际应用中,对于规则六面体格网,可针对实际模型进行计算以确定最佳的平滑系数γ值,也可简单地取区间[0.26, 0.29]中值0.275为γ近似值。
对于不规则六面体网格,由于实际地层分界面和地质模型的多样性,上述的区间并不适用,需针对具体情况进行计算以获取最优的γ值。但拐点现象是存在的,因为评价指标为平滑顶点与相邻顶点连线形成的夹角余弦值或余弦平均值,夹角总是在[0, 360°]之间变化,其余弦曲线总是具有拐点位置(图9)。
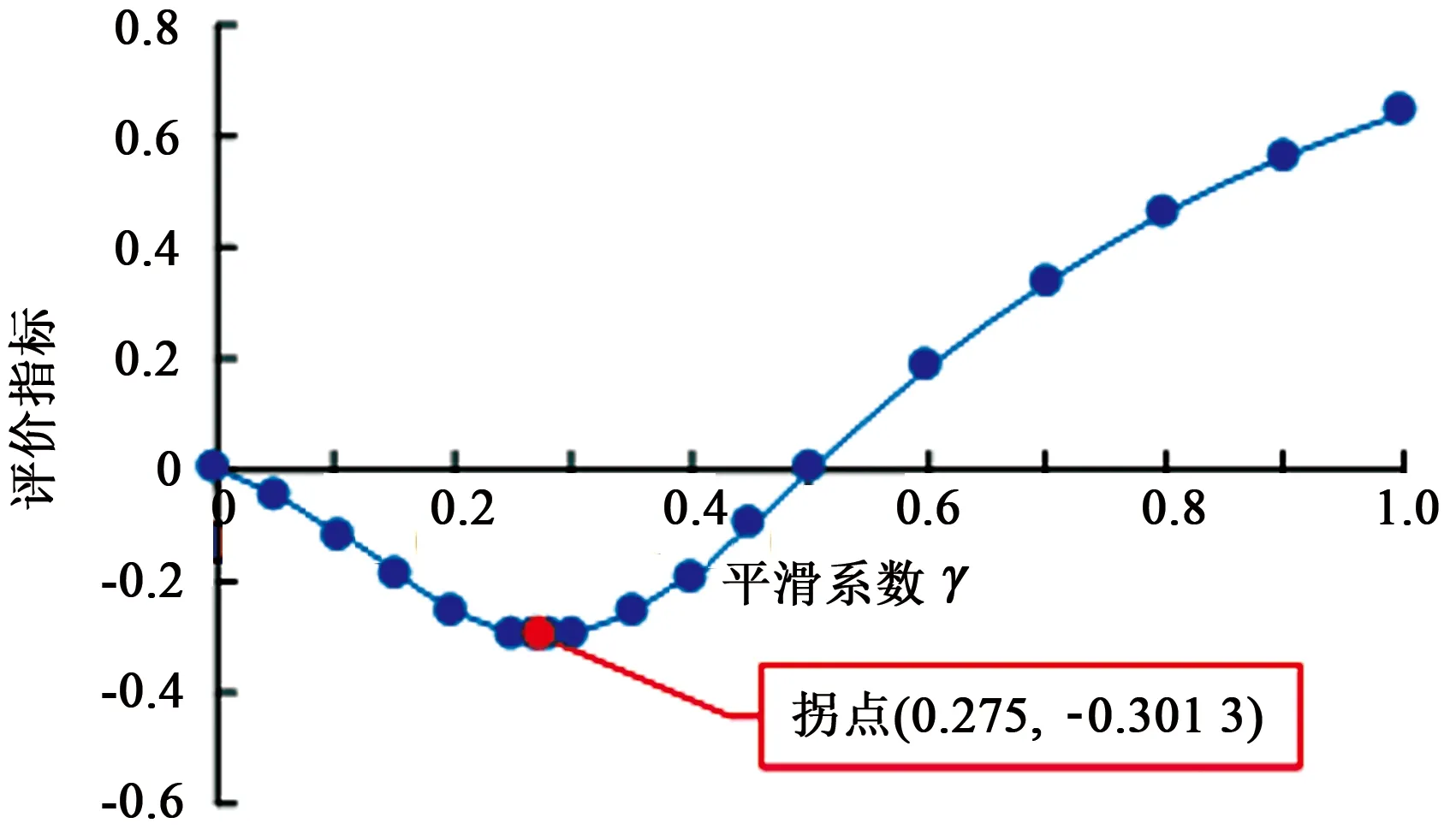
图11平滑系数和评价指标的关系曲线Fig.11 Curve between smoothing factor and evaluation index
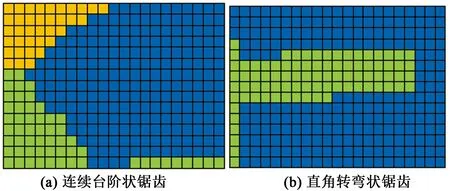
图12 两种锯齿现象Fig.12 Two kinds of jaggies
4.2 算法应用
采用C++及OSG(OpenSceneGraph)三维引擎,以自主研发的Simtools油藏模拟分析软件为平台,对基于邻域网格作用力的三维网格平滑方法进行了实现,并加载了实际的三角洲沉积相数据,加载数据的网格规模为97×105×8,网格平均大小为200 m×200 m×30 m。图13~15分别为平滑前后俯视图效果对比、俯视图局部细节对比及剖面效果对比,可以看出,通过对沉积相边界的平滑处理,模型的可视化效果有了较大的改善。
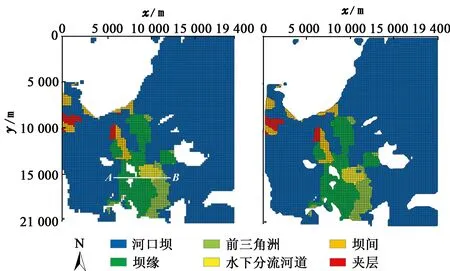
图13 平滑前后俯视图效果对比Fig.13 Effect contrast of top view before and after smoothing
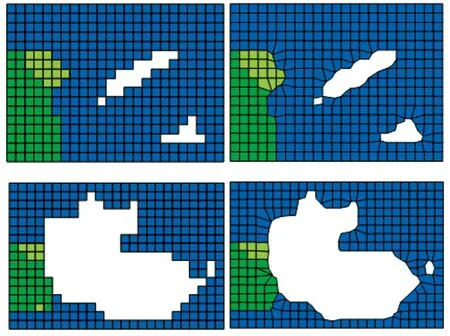
图14 平滑前后局部细节对比Fig.14 Local details contrast of top view before and after smoothing
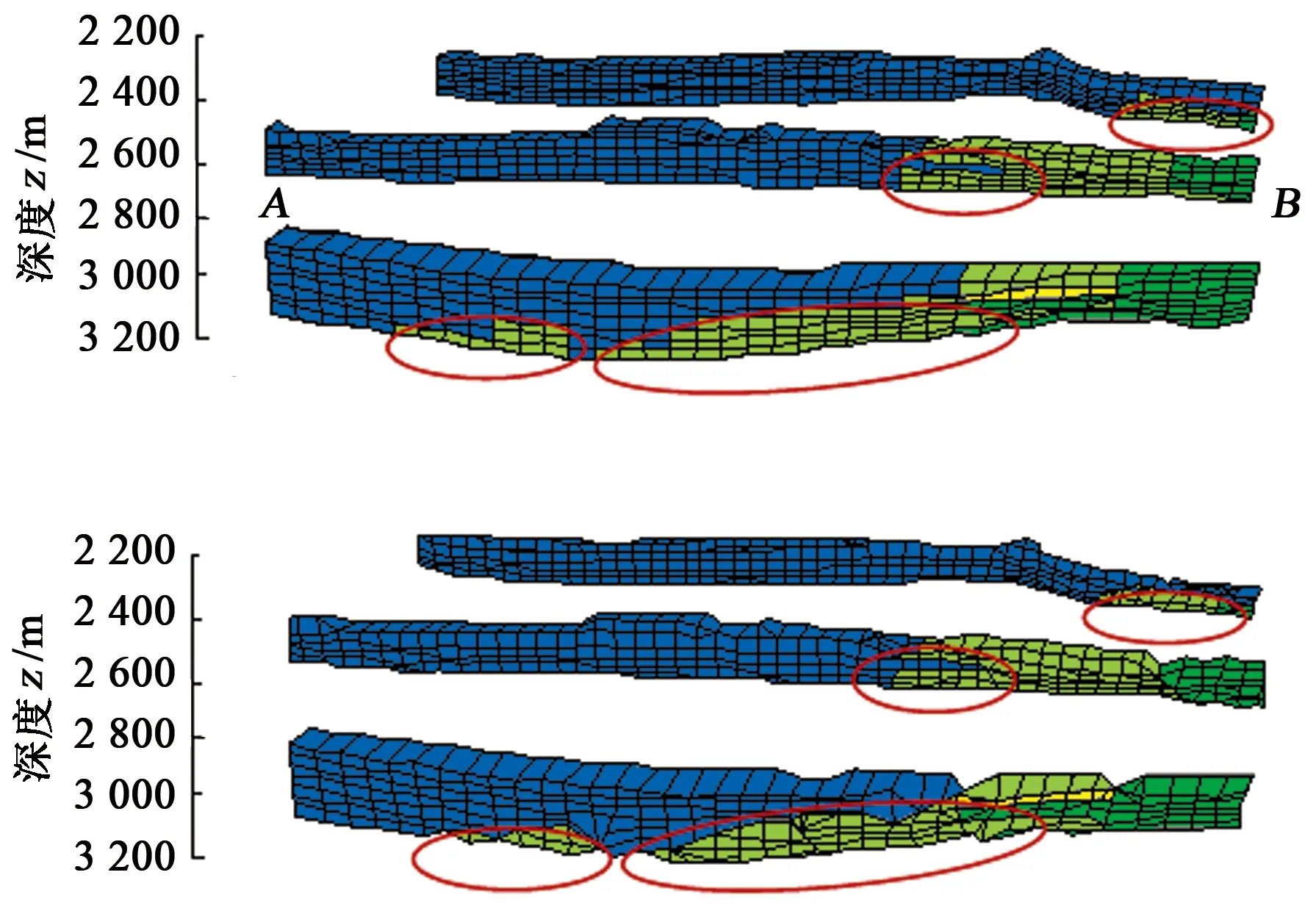
图15 平滑前后三维模型部分剖面对比Fig.15 Part profile contrast of 3D model before and after smoothing
5 结束语
基于邻域网格作用力的三维网格体平滑方法,充分利用六面体网格数据组织形式,以IJK对顶点及其邻域网格进行遍历,简单、快速。算法对需平滑顶点的邻域网格根据属性值划分为不同的体块,根据体块对顶点的作用合力方向确定顶点平滑移动的方向,通过移动方向的邻域网格对角线长度限制顶点移动的最大距离,使顶点平滑距离不超出邻域网格的范围,从而在平滑过程中完全保持了网格原有的拓扑关系。本方法基于“互斥作用力”的平滑思路不仅可以用于六面体网格的二、三维平滑,也可以推广到其他类型基元构成的三维模型,如四面体网格、三棱柱网格等。三维地质体、油藏体模型使用的角点网格需对尖灭、缺失、断层等地质现象建模,导致网格模型存在着无效网格或邻域网格不共点等复杂情况。下一步工作将具体分析特殊情况下邻域网格的查找方式,对三维网格体平滑方法进行完善和优化。
[1] 武强,徐华.三维地质建模与可视化方法研究[J].中国科学(D辑):地球科学,2004,34(1):54-60.
WU Qiang, XU Hua. On three-dimensional geological modeling and visualization[J]. Science in China(Ser D): Earth Sciences, 2004,47(8):739-748.
[2] 赵永军,舒晓,胡勇,等.一种复杂曲流带储层三维构型建模新方法[J].中国石油大学学报(自然科学版),2015,39(1):1-7.
ZHAO Yongjun, SHU Xiao, HU Yong, et al. A new 3D architecture modeling method of complex meander belt reservoir[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015,39(1):1-7.
[3] 林承焰,董春梅,任丽华,等.油藏描述技术发展及启示[J].中国石油大学学报(自然科学版),2013,37(5):22-27.
LIN Chengyan, DONG Chunmei, REN Lihua, et al. Development of reservoir characterization and its stimulation[J]. Journal of China University of Petroleum (Edition of Natural Science), 2013,37(5):22-27.
[4] 毛小平,张志庭,钱真.用角点网格模型表达地质模型的剖析及在油气成藏过程模拟中的应用[J].地质学刊,2012,36(3):265-273.
MAO Xiaoping, ZHANG Zhiting, QIAN Zhen. Analysis of geological model expressed by corner point grid model and application in process of simulation of hydrocarbon accumulation process[J]. Journal of Geology, 2012,36(3):265-273.
[5] 刘慧卿,马代鑫,张松亭.精细油藏描述数据的粗化方法研究[J].石油大学学报(自然科学版),2003,27(6):36-38.
LIU Huiqing, MA Daixin, ZHANG Songting. Up-scaling technique for handling data of fine reservoir description[J]. Journal of the University of Petroleum, China (Edition of Natural Science),2003,27(6):36-38.
[6] KWAK D Y, IM Y T. Remeshing for metal forming simulations-Part II: three-dimensional hexahedral mesh generation[J]. International Journal for Numerical Methods in Engineering, 2002,53(11):2501-2528.
[7] HENGL T. A practical guide to geostatistical mapping[M].Amsterdam: University of Amsterdam, 2009:117-128.
[8] 李光明,田捷,何晖光,等.基于距离均衡化的网格平滑算法[J].计算机辅助设计与图形学学报,2002,14(9):820-823.
LI Guangming, TIAN Jie, HE Huiguang, et al. A mesh smoothing algorithm based on distance equalization[J]. Journal of Computer-Aided Design & Computer Graphics, 2002,14(9):820-823.
[9] 佟一飞.基于顶点扩散的三维网格平滑技术研究[D].大连:辽宁师范大学,2008.
TONG Yifei. Research on the smoothing techniques for 3-D mesh based on vertex diffusion[D]. Dalian: Liaoning Normal University, 2008.
[10] KIM M, LEE J. A data transformation method for visualizing the statistical information based on the grid[J]. Journal of Korea Spatial Information Society, 2015,23(5):31-40.
[11] KORDI M, FOTHERINGHAM A S. Spatially weighted interaction models (SWIM)[J]. Annals of the American Association of Geographers, 2016,106(5):990-1012.
[12] RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm[J]. Information Sciences, 2009,179(13):2232-2248.
A3Dmeshessmoothingmethodbasedonneighborhoodforces
WANG Haiqi1, PENG Jiaqi1, WANG Yi1, DONG Qiannan1, CHE Lei1, GONG Weiqing2
(1.SchoolofGeosciencesinChinaUniversityofPetroleum,Qingdao266580,China;2.SINOPECResearchInstituteofPetroleumExploration&Development,Beijing100083,China)
Hexahedral meshes are widely used to build three-dimensional (3D) geological and reservoir models. However, this voxel model, derived from rectangular grid, has jagged effects when modeling the boundary of a 3D region, which is not consistent with actual geological phenomena. To address the jagged-edge phenomena, under the condition of keeping original topology structure invariable, a smoothing algorithm is proposed based on the forces of neighborhood meshes. The algorithm is inspired by "poles repel" derived from physical properties of a magnet, and the neighboring meshes of a smoothed vertex are divided into different blocks according to their attributes. The blocks have repulsive force. The direction and magnitude of resultant force determine the vertex direction and distance of smoothing movement. The practical application shows that there is an inflection point for smoothing performance and the smoothing performs better when the smoothing coefficient closes to the inflection point; or conversely, the performance is decreasing when smoothing coefficient is away from the inflection point.
hexahedral mesh; jagged effect; 3D smoothing; neighborhood mesh; force
2017-02-02
国家自然科学基金项目(41471322); 山东省自然科学基金项目(ZR2012DM010)
王海起(1972-), 男, 副教授, 博士, 研究方向为地理信息系统与数字油田。E-mail: wanghaiqi@upc.edu.cn。
1673-5005(2017)06-0080-08
10.3969/j.issn.1673-5005.2017.06.009
TP 391.9
A
王海起,彭佳琦,王艺,等.一种基于邻域作用力的三维网格平滑方法[J].中国石油大学学报(自然科学版),2017,41(6):80-87.
WANG Haiqi, PENG Jiaqi, WANG Yi, et al. A 3D meshes smoothing method based on neighborhood forces[J].Journal of China University of Petroleum(Edition of Natural Science), 2017,41(6):80-87.
(编辑 修荣荣)

