探索关系 相互转换

仇招成

在丰富的图形世界里，“点”的灵动轻盈成就柔和的曲线之美，“线”的柔美形态造就“面”的恢弘大气，点、线、面的完美集成构就“体”的不同性格：可以刚硬、可以柔美、可以开放、可以封闭……在此，让我们一起来回顾三视图的解题要点.

例1 （2017·扬州）经过圆锥顶点的截面的形状可能是（ ）.

例2 （2004·宿迁）图1是一块带有圆形空洞和方形空洞的木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（ ）.

【解析】因圆锥顶点到底面圆周上任一点的连线段（母线）相等，故例1中B正确.

根据三视图知识，圆柱的主视图（左视图）是矩形，可以堵住方形空洞，圆柱的俯视图是圆，可以堵住圆形空洞，故例2中B正确.

【说明】三视图就是主视图、左视图、俯视图的总称.一个视图只能反映物体的一个方位的形状，不能完整反映物体的结构形状.

一个平面与一个几何体相交所截得的图形叫做截面.截面的形状随截法的不同而改变，一般的截面与几何体的几个面相交就得到几条交线，截面就是几边形.

三视图和截面在方法、角度上是不同的.我们需要根据具体要求来确定平面图形的“形状”.

（1）写出这个几何体的名称；

（2）任意画出这个几何体的一种表面展开图；

（3）若俯视图中正三角形的边长为4cm，左视图中长方形的高为10cm，求这个几何体的侧面积.

【解析】（1）只有棱柱的主视图和左视图才能出现长方形，根据俯视图是三角形，可得到此几何体为三棱柱；

（2）应该会出现3个长方形，2个三角形；（图略）

（3）侧面积为3个长方形，计算出一个长方形的面积，乘3即可（3×10×4=120cm2）.

【说明】以“简单几何体的三个视图”为中心，我们通过想象、模拟、分析、推理，感受三视图与简单几何体之间的相互转化，体验二维与三维空间相互转换关系.我们除了要关注“形状”“位置”（方位）外，还需关注“数量”关系，即主视图和俯视图的长相等；主视图和左视图的高相等；左视图和俯视图的宽相等.

例4 把边长为2cm的6个相同正方体摆成如图3的形状.

（1）画出该几何体的主视图、左视图、俯视图；

（2）试求出其表面积；

（3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的左视图和俯视图不变，那么最多可以再添加__________个小正方体.

【解析】（1）

（2）计算出三视图（平面图形）的面积和，然后乘2，再加2个正方形的面积（从三个方向都看不见的部分）即可：2×[2×2×（4+3+5）]+2×2×2=104cm2.

（3）利用左视图和俯视图不变，得出可以添加小正方体的位置.故最多可以再添加2个小正方体.

【说明】几何体的三视图从微观和局部反映了几何体的结构和大小，对于简单的几何体或组合体的表（侧）面积，可利用三视图中隐含的几何条件，直接计算几何体表面的所有平面图形的面积和即可（注意：避免重复计算和漏算）.

一般来说，已知三视图可以确定一个几何体，但已知两个视图不一定能确定几何体.在三个视图中，俯视图最重要，它可以直接确定底层有几个正方体，再由主视图、左视图确定几层数及每层的个数.具体方法如下：

（1）由俯視图、左视图（主视图）来确定小正方体个数：

以例4第（3）问为例：①先复制一张俯视图，俯视图的左方（下方）标注左视图（主视图）所看到的小正方体的最高层数；将这些数字填入所在行（列）的每一个方格，则可得到这个几何体所需最多的小正方体的块数；②将每行（列）上数字只留一个，其余的均改为1，这样就可以确定最少需要的小正方体的块数.

（2）由主视图、左视图来确定小正方体个数：

还是以例4的主视图、左视图为例：

①先根据主视图和左视图确定俯视图最大是2×3的方格；

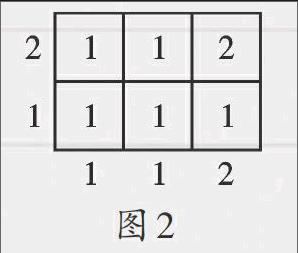
在方格下方、左方分别标上主视图、左视图所看到的小正方体的最高层数.然后，在方格中填入所在行、列上的较小数字，那么就可以确定这个几何体所需最多小正方体的块数（如图2所示）.

②在方格中寻找所在行和列方向上的数字一样的方格，取相同的数字填入方格，这样就可以确定最少需要的小正方体的块数（如图3所示）.

（作者单位：江苏省南京市第二十九中学初中部）endprint