立体织机打纬机构动力学方程的对称性解法

郑明亮



立体织机打纬机构动力学方程的对称性解法

郑明亮

（浙江理工大学 机械与控制学院，浙江 杭州 310018）

曲柄滑块式打纬机构广泛应用于立体织机平行打纬中，对其进行全面深入准确的动力学特性研究，将有助于提升织机整体性能，提高生产效率。本文主要基于Lie对称性理论精确计算了立体织机打纬机构的动力学方程，以此克服位置非线性数值分析以及与设计参数定量显示关系的困难。首先，在考虑打纬机构的非线性几何约束，依据分析力学方法建立了两自由度打纬机构动力学模型；其次，运用首次积分法得到机构性能指标打纬力的解析动态响应曲线，并进行了连续性局部参数灵敏度分析；最后，实际算例表明用对称性理论研究机构非线性动力学特性，方法新颖，适用范围广，结果可靠准确，本文的研究内容也为织机打纬机构更精确地动态优化设计和先进控制奠定了理论基础。

打纬机构；非线性约束；Lie对称性；打纬力

0 引言

立体织造技术是一种新型纺织技术，它使纱线在三维空间中沿着多个方向分布并相互交织在一起形成不分层的整体结构，由它作为碳纤维增强体制成的复合材料具有一系列优异的性能[1-2]，近年来在航空、汽车、能源、航天、运动器材、交通等许多领域得到飞速发展。打纬运动是三维立体织造中非常重要的核心环节，它的设计将会影响引纬机构、开口机构，还直接关系到碳纤维织物的形成。现有碳纤维立体织机打纬机构普遍采用的是的曲柄滑块装置同步驱动钢筘垂直入纬，实现平行打纬[3-5]，通过控制曲柄滑块机构伺服电机的输入参数实现变打纬力输出，可适应不同层数、不同规格立体织物的打纬力需求。在织造过程中，打纬力必须大于打纬阻力，才能顺利完成打纬运动动作。因此，打纬力的精确计算和校核是设计打纬机构的基础和关键[6-7]。建立打纬机构动力学模型并利用现代分析力学方法开展研究，对于改善织机织造工艺性能有重要意义。

目前对织机打纬机构的研究仅停留在简单动力学建模和运动学研究上，或者应用虚拟软件对机构进行动态建模获取其动态性能指标。无论理论求解和软件仿真计算都多以数值手段为主，即采用数值积分方法，计算系统的动力学响应，从而分析系统中存在的运动现象和力学特性[8-13]。而在机构动力学方程方程精确解析解求方面一直很少有文献涉及，由于困难重重，尚处于起步阶段。Lie对称性理论在处理线性和非线性、常系数和变系数微分方程的问题都是等同的，它和其他的现代分析方法一起，是求常-偏微分方程的解析解的最可能统一的通用工具，可以用来进行大范围的全局动力学研究，且计算过程易于程序化特点[14]。国内外关于利用Lie对称性方法解析研究立体织机打纬机构动力学还未有报道。本文基于Lie对称性方法对打纬机构的动态性能响应进行研究，进而指出系统参数对机构动态特性的影响，为实现打纬机构的优化设计和合理控制策略提供理论依据。

1 动力学系统的Lie对称性理论

设完整约束非奇异力学Lagrange系统以广义加速度形式的微分方程为：

引进时间和坐标的特殊无限小变换：

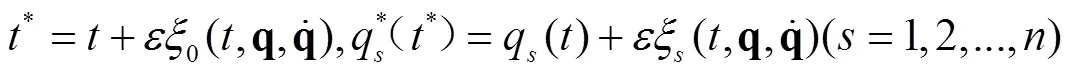
微分运动方程的Lie对称性是指方程(1-1)在上述无限小变换（2）下形式不变[15]，即：

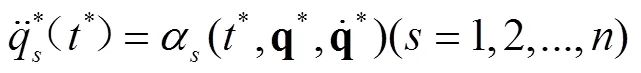
上式也可以表述成Lie对称性确定方程：

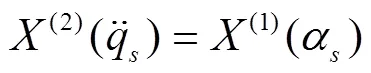
Lie确定方程(1-4)展开形式为：

微分方程群分析是用来寻找微分方程的对称性，连续变换的对称性都对应着一条守恒定律，一个守恒量对应一个首次积分，进而系统微分方程达到降阶和约化，守恒律在微分方程的可积性、线性化、运动常数方面有重要作用。Lie对称性在一定条件下可直接导致新型守恒量，再结合初始条件，从而很容易解出原高阶系统的精确响应解。

成立，则系统Lie对称性对应的守恒量表达式为[15]：

2 立体织机打纬机构动力学模型

普通织机主要用于织造平面织物，钢筘的运动轨迹为圆弧，属于摆动打纬，很难将立体织物的数根纬纱同时打入织口，并使每根纬纱所受到的打击力相等，因此，对立体织物的平行打纬动作需要使用前后往复运动规律，借用普通织机打纬运动设计思想，根据机构学当四杆机构中有一连杆为曲柄，另一连杆相对机架作往复移动而成为滑块时，四杆机构就变成曲柄滑块机构，选择对心曲柄滑块式立体织机打纬机构作为研究对象，如图1。

图1 打纬机构的三维实体图

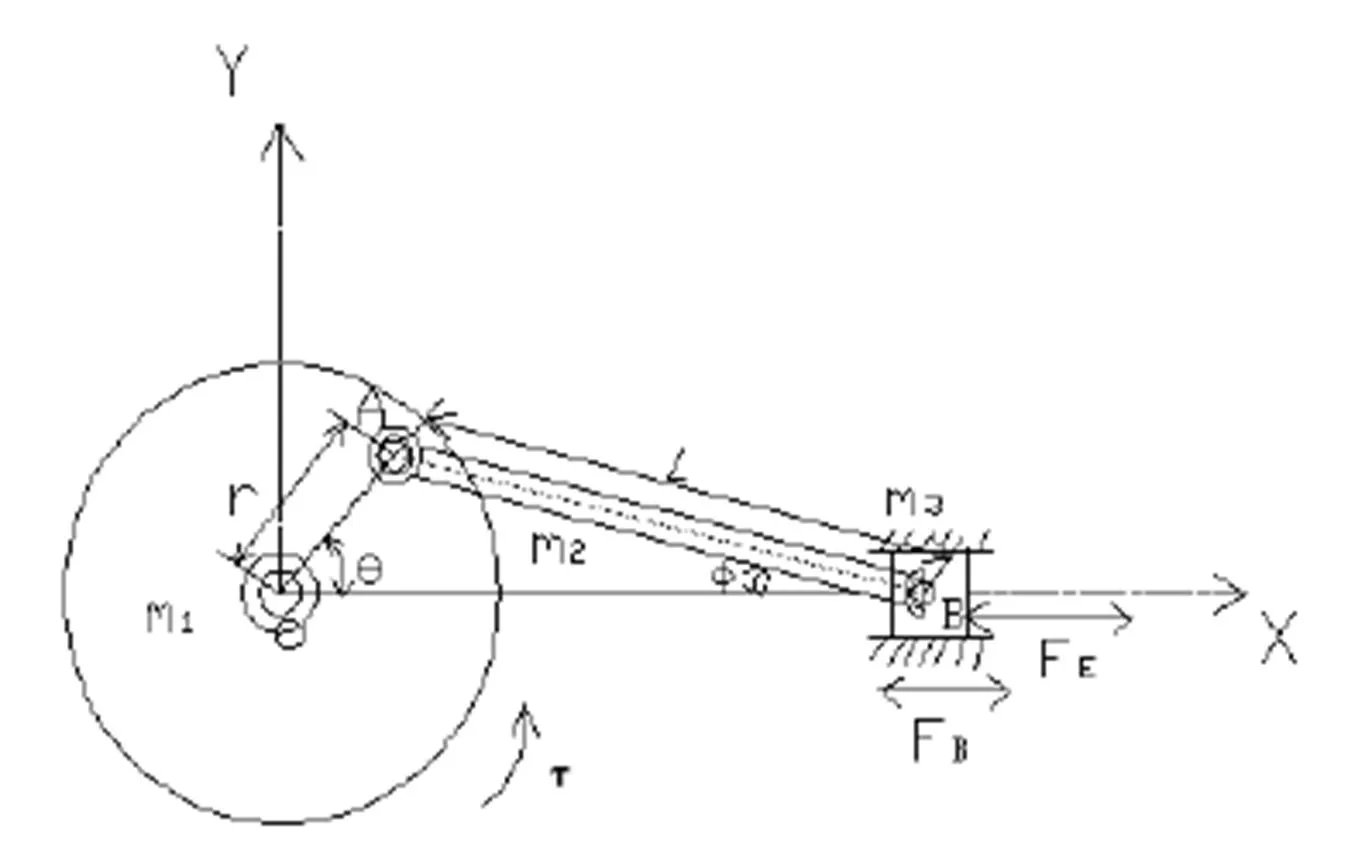
图2 曲柄滑块打纬机构示意图

当织机运转速度不是很高时，可以将打纬机构的所有构件看作刚性体，同时考虑到本文是首次用力学系统的对称性理论去分析机械多体系统的动力学特性，解析求解微分方程的自由度不应过多，本着能说明问题和方法的可行性原则，所以本文暂时不考虑织机打纬机构运动副间隙、构件的弹性变形以及机电耦合等因素。其机构示意图如图2所示。

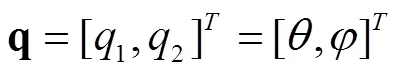
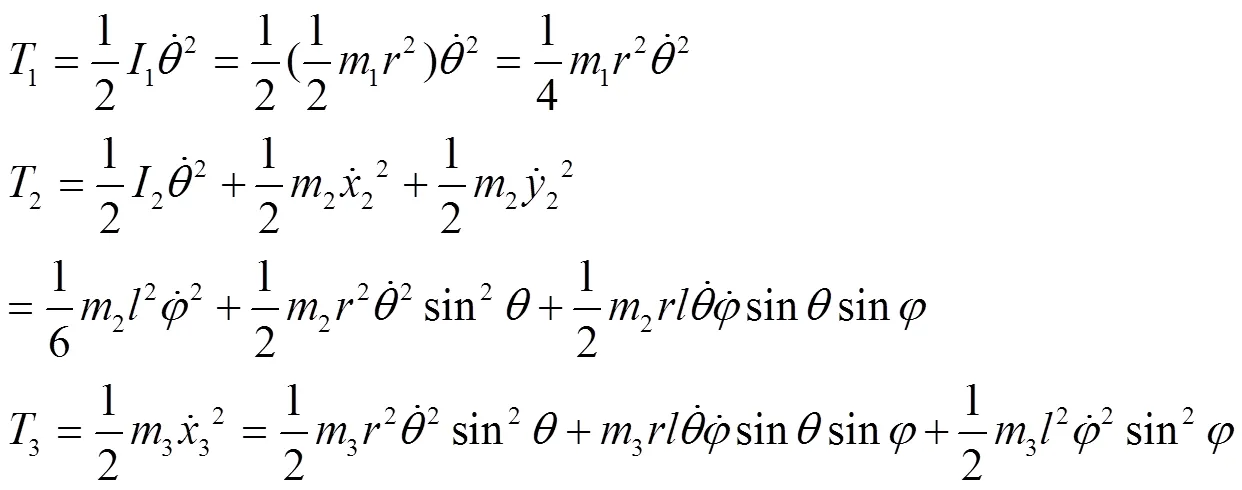
转盘，连杆和滑块的重力势能分别为：

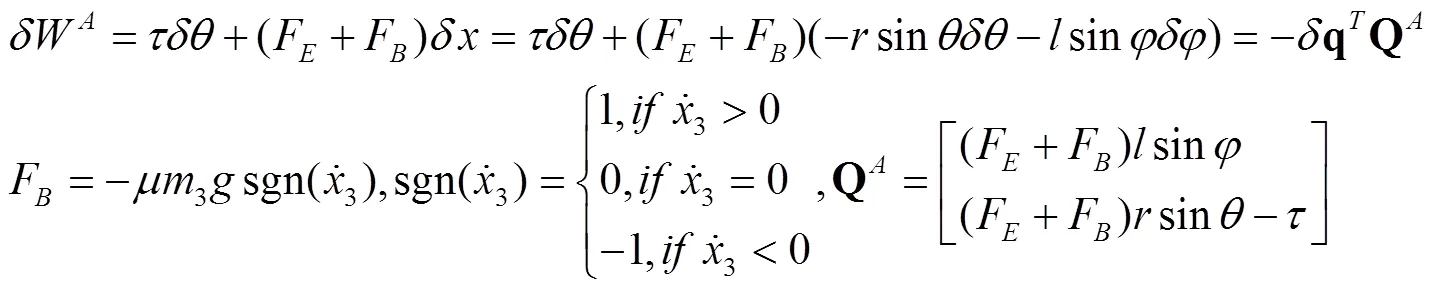
由矢量封闭三角形可知，机构有以下明显非线性几何约束条件：

整理式(14)可得到多体动力学欧拉-拉格朗日方程：

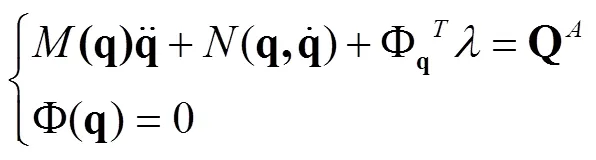
其中

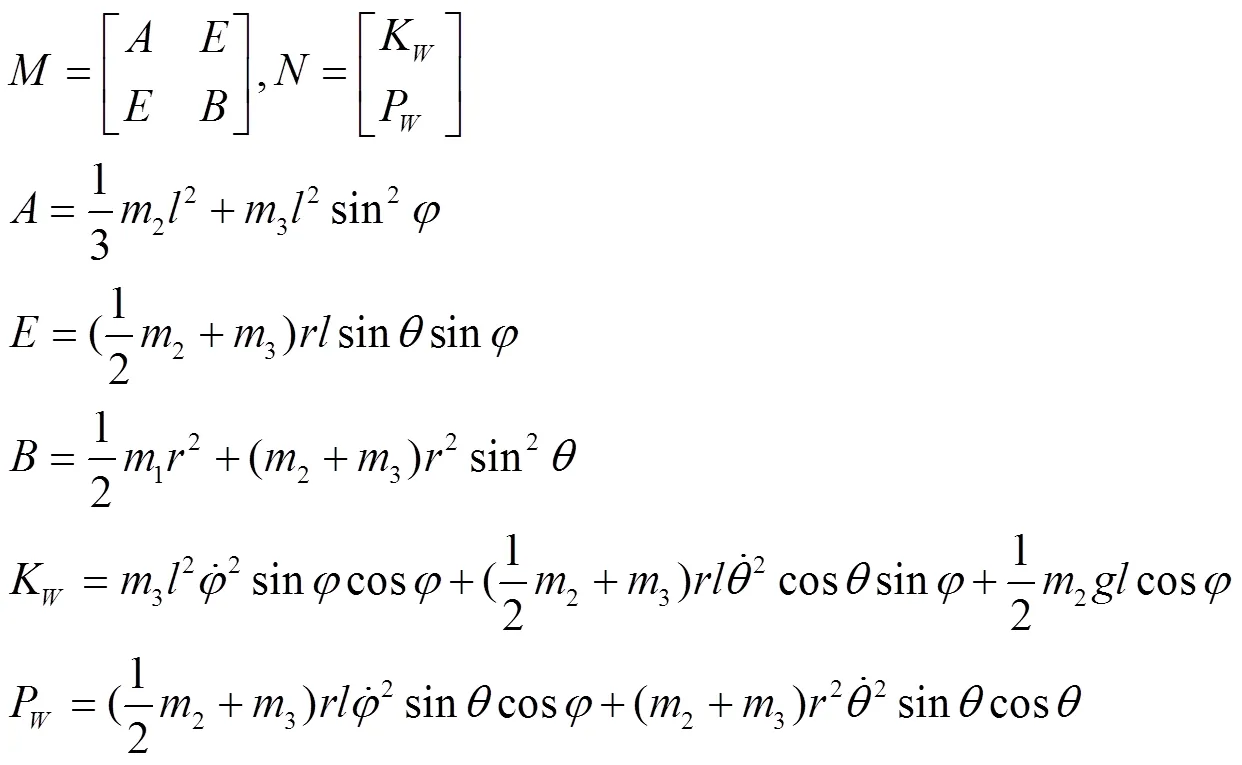
3 打纬机构的动态特性分析

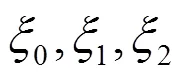
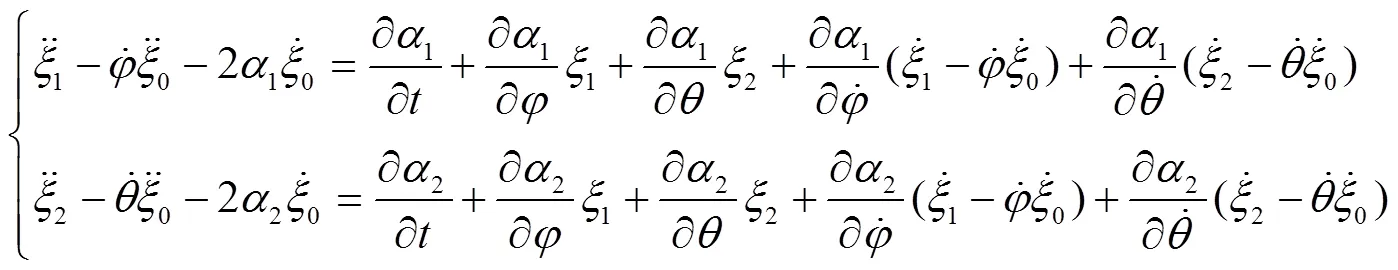
上述方程的解将非常困难，为此我们从系统本身的一些具体特性出发，易知此约束系统有广义能量守恒，显然易得到：

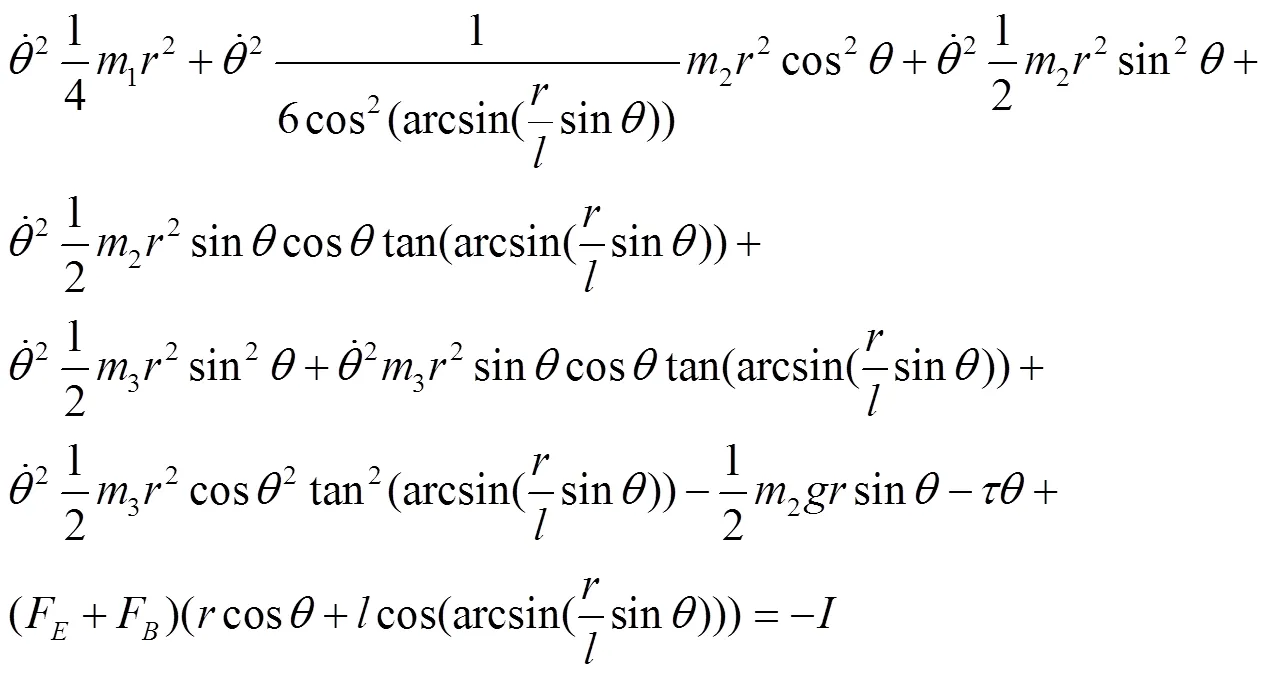
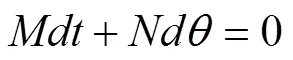
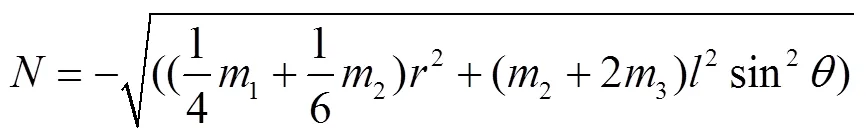
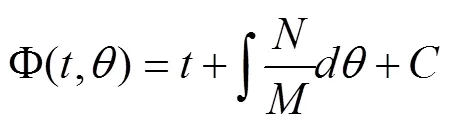
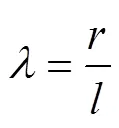
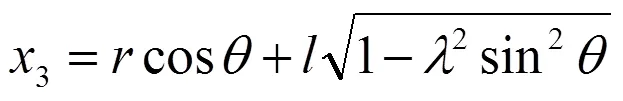
惯性打纬力计算公式如下：

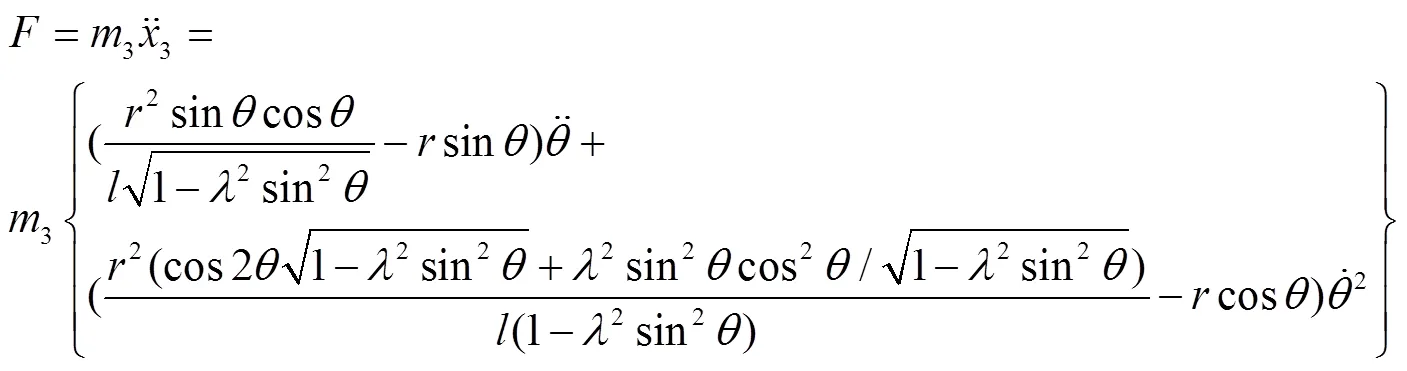
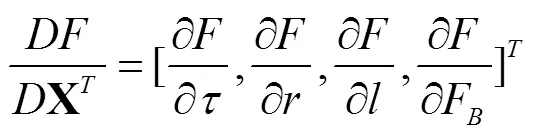
对于具体的织机结构模型，可以进一步计算打纬性能指标对设计参数的灵敏度数值大小。

4 实际例子说明

以普通某型立体织机为例进行打纬机构的动力学特性分析，打纬过程中钢筘所受的打纬阻力基本由两部分构成：一是纬纱在运动过程中与经纱摩擦所受的摩擦阻力，二是经纱对纬纱的弹性阻力打纬阻力由经纱、纬纱之间的摩擦阻力和弹性阻力组成，大小主要取决于纱线种类、经纱张力、经纱角、纬密、经密和幅宽等因素，计算过程复杂，计算详细可参见文献[16]。打纬阻力和驱动力精确数值一般由试验系统，系统具体设计参数示于表1中：

表1 曲柄滑块机构的相关设计参数

图3 曲柄转角变化曲线图

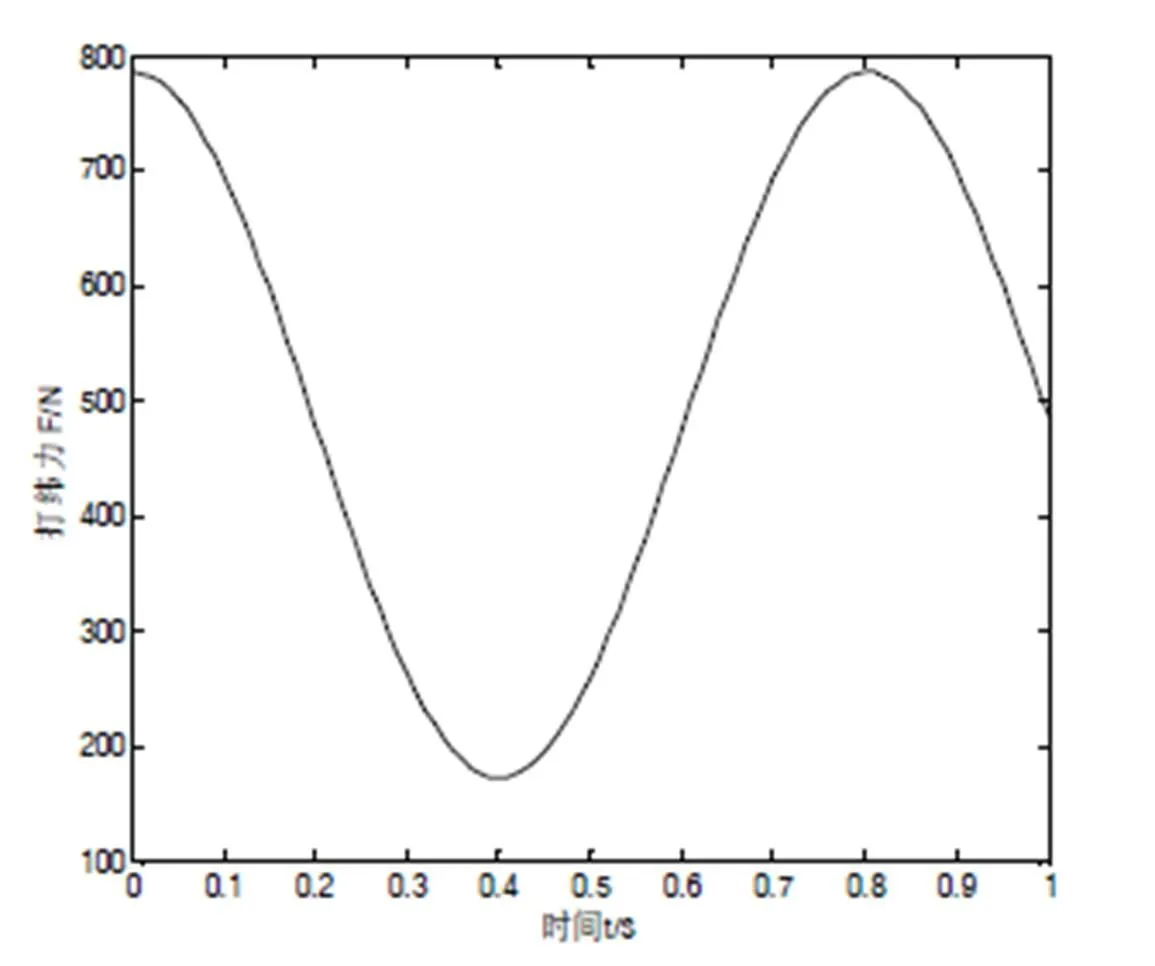
图4 打纬力变化曲线图

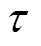
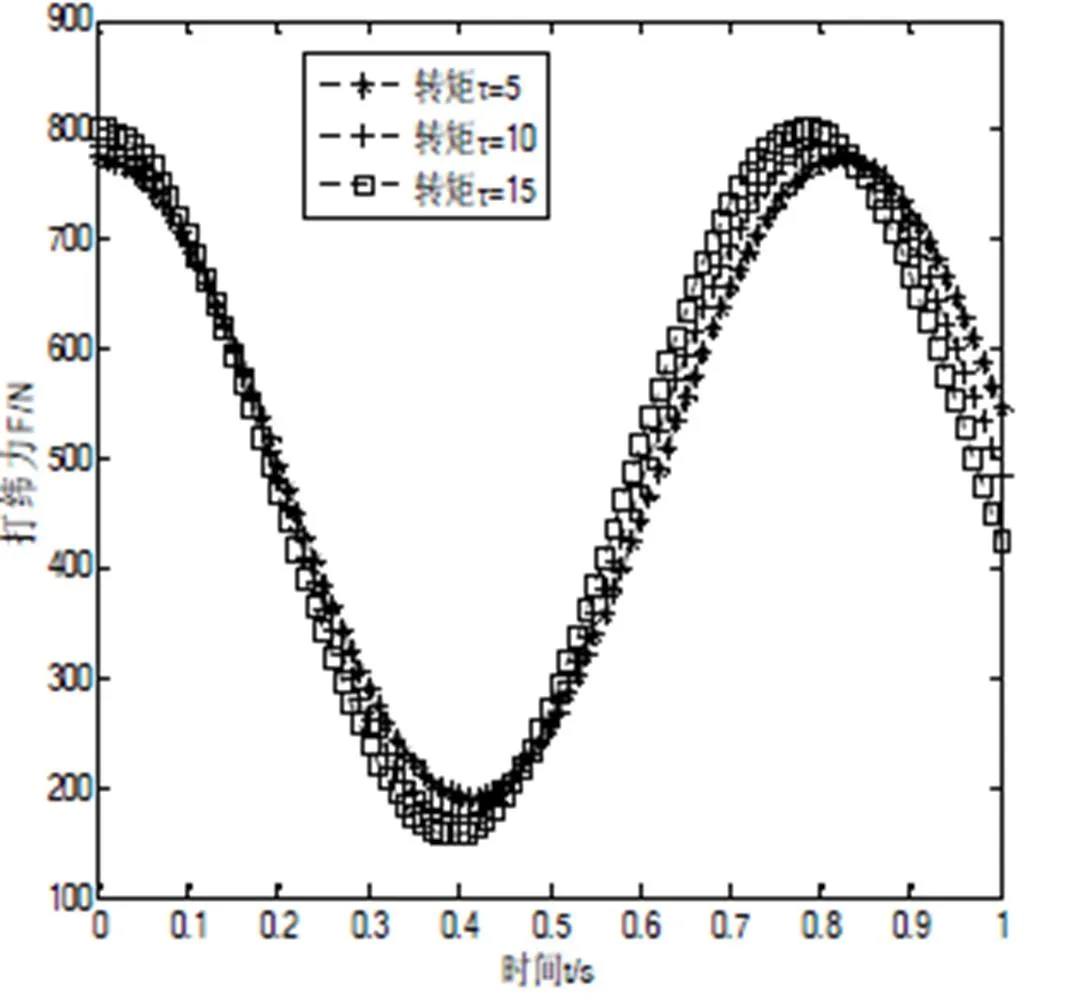
图5 打纬力与驱动力矩变化图

图6 打纬力与尺寸比变化图

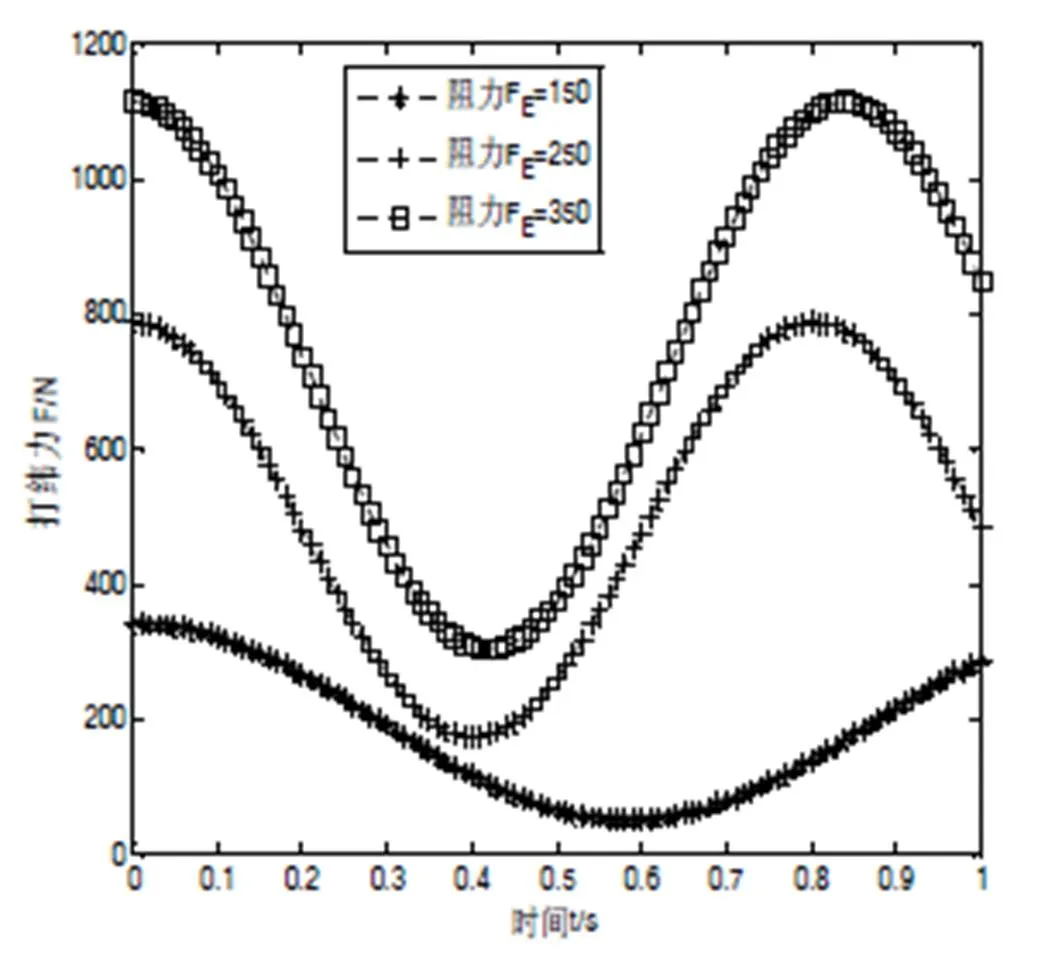
图7 打纬力与阻力变化图

图7基本可表明，尺寸比和打纬阻力的作用足以影响打纬性能，尺寸长度比与打纬性能关影响系最明显，打纬阻力影响也是较明显的，转矩对机构加速度影响不明显。因此，单纯增加打纬机构电机驱动来提升动态性能的方式并非行之有效的方法，应综合考虑织机转速、结构尺寸、织物种类并结合打纬机构其他方向变形带来的影响来综合参数匹配。

5 结语

本文应用分析力学方法建立了立体织机打纬机构系统两自由度动力学模型，用Lie对称法计算了系统机构精确的动态性能指标打纬力变化规律曲线，并指明了一些设计参数对其变化的影响关系。结果表明，Lie分析方法对于求解非线性方程具有良好的扩展性，是高效、准确的，可以为含复杂因素的打纬机构动力学特性提供有用的分析工具。同时，本文的内容也为打纬机构打纬力的精确控制方法和结构优化提高奠定了基础。

[1] 杨建成, 姜海涛, 蒋秀明. 碳纤维立体织机打纬机构运动特性仿真[J]. 天津工业大学学报, 2016，6(3): 83-88.

[2] 姚孟利. 研究碳纤维立体织造装备为发展纤维增强复合材料提供技术保障[J]. 纺织机械, 2012，(3): 2-5.

[3] 李佳. 立体织机经纱系统和打纬机构的设计[D]. 上海: 东华大学, 2013.

[4] 姜海涛. 碳纤维立体织机打纬机构优化与工艺研究[D]. 天津: 天津工业大学, 2015.

[5] 张立泉. 三维机织结构设计和织造技术的研究[J]. 玻璃纤维, 2002，(2): 3-7.

[6] MASC'HINENWESEN V D F. Development of the weaving machine and 3D woven spacer fabric structures for lightweight composites materials[D]. Dresden: Technische Universitat Dresden, 2007.

[7] UOKARNESHANA N, ALAUIRUSAMYB R. Weaving of 3D fabrics: A critical appreciation of the developments[J]. Textile Progress, 2009, 41(1): 1-58.

[8] YAN H S, YEH C C. Integrated kinematics and dynamic designs for variable-speed plate cram mechanisms [J]. Journal of Mechanical Engineering Seience, 2011, 225(1):194-203.

[9] 金玉珍, 胡小冬. 喷气织机打纬机构及墙板的振动特性[J]. 纺织学报, 2016, 7(37): 132-138.

[10]陈静, 冯志华. 喷气织机四连杆打纬机构动态响应的数值解[J]. 苏州大学学报(自然科学版), 2006, 2(22): 48-51.

[11]金国光, 秦凯旋，等. 剑杆织机柔性从动件共轭凸轮打纬机构动力学分析[J]. 纺织学报, 2016, 5(37): 137-142.

[12]魏展, 金国光，等. 高速共轭凸轮打纬机构柔性动力学分析[J]. 机械工程学报, 2017, 3(53):81-90.

[13]孙中奎, 冯志华，等. 喷气织机六连杆打纬机构动态特性分析与优化[J]. 苏州大学学报(工科版), 2011, 4(31):48-51.

[14]田畴. 李群及其在微分方程中的应用[M]. 北京：科学出版社, 2003.

[15]梅凤翔. 李群和李代数对约束力学系统的应用[M]. 北京：科学出版社，1999.

[16]吴强, 李佳, 陈革. 立体织造打纬阻力的计算[J]. 东华大学学报(自然科学版), 2013, 5(39): 614-617.

Symmetry Solution of Dynamic Equations of Weft Beating Mechanism of Stereo Loom

ZHENG Ming-liang

(School of mechanical engineering, Zhejiang Sci-Tech University, Hangzhou Zhejiang 310018, China)

The slider crank beating up mechanism is widely used in the parallel beating up of three dimensional looms. It is helpful to improve the overall performance of the loom and increase the production efficiency by studying the dynamics characteristics comprehensively and accurately. In this paper, the dynamic equations of the weft beating mechanism of a solid loom are calculated accurately based on the Lie symmetry method, in order to overcome the difficulty of the position nonlinear numerical analysis and the quantitative display of the design parameters. First, considering the nonlinear geometric constraint of beating up mechanism, a dynamic model of two degree of freedom beating up mechanism is established according to the analytical mechanics method; secondly, the analytical dynamic response curve of beating force of mechanism performance index is obtained by the first integral method, and the continuous local parameter sensitivity analysis is also carried out; finally, the practical example shows that the theory of symmetry can be used to study the nonlinear dynamic characteristics of mechanisms. The method is novel, applicable to a wide range, reliable and accurate. The research content of this paper lays a theoretical foundation for more accurate dynamic optimization design and advanced control of loom beating up mechanism.

beating up mechanism; nonlinear constraint; Lie symmetry; beating force

Th122.0322

A

2095－414X(2017)06－0037－07

郑明亮（1988-），男，博士研究生，研究方向：机械振动与动力学控制.