基于Abaqus的橡胶扭振减振器胶圈失效分析
胡鸿飞,郭一鸣,肖祖玉,甘新刚
(1.湖北汽车工业学院 汽车工程学院,湖北 十堰 442002;2.湖北广奥减振器制造有限公司,湖北 十堰 442000)
基于Abaqus的橡胶扭振减振器胶圈失效分析
胡鸿飞1,郭一鸣1,肖祖玉2,甘新刚2
(1.湖北汽车工业学院 汽车工程学院,湖北 十堰 442002;2.湖北广奥减振器制造有限公司,湖北 十堰 442000)
运用Abaqus对不同厚度的橡胶圈在不同鼓形结构的减振器下的压入力、压脱力和滑移扭矩进行了仿真试算,并做实验得到实测值,确定了摩擦系数。基于正交试验设计,探讨了鼓形长度、鼓形高度及橡胶圈压缩比对压入力、压脱力、滑移扭矩大小的影响程度,对解决生产实践中的橡胶圈失效问题具有一定的指导意义。
有限元分析;正交试验设计;橡胶圈失效
发动机曲轴系统产生扭转振动,内因是轴系本身具有惯性且有弹性,而外因是作用在轴系上周期性变化的激振力矩[1]。当激振频率与轴系固有频率相同时,就会产生共振现象,通过安装橡胶扭振减振器以改变轴系的固有频率是发动机减振问题最直接有效的方法。橡胶扭振减振器是扭振减振器的一种,这类减振器可利用橡胶弹性产生的反力矩抵消一部分振动力矩,还可利用橡胶的内部阻尼来消耗振动能量。橡胶圈是橡胶扭振减振器的重要部件,橡胶圈失效是近年来市场上经常出现的问题。失效原因分为2种情形:在压装过程中,由于减振器内部鼓形结构不合理或轮毂与惯量环间的间隙太小(压缩比相对太大),压入时会导致橡胶圈破损失效;在发动机工作过程中,发动机附件大转矩和发动机扭转激励的长期作用下,减振器的轮毂和橡胶圈之间会产生滑移失效,惯性环和轮毂之间易产生横向振动,会引起非周期性的横向拉力,进而导致橡胶圈脱落失效[2]。在减振器装机前,通常进行静扭矩试验和压脱试验来确定其滑移扭矩和压脱力是十分必要的,但对不同结构参数的样件都进行实验测试耗费财力物力。
经长期的生产实践发现,橡胶圈压缩比的选择以及减振器结构的设计可直接影响橡胶圈是否失效。前人研究了橡胶圈形状对滑移扭矩的影响[3],未能系统地研究减振器的结构与橡胶圈压缩比对减振器性能的影响。为探讨各因素对减振器性能的影响,文中基于正交试验设计法用有限元软件对某型号橡胶扭振减振器橡胶圈的压入力、压脱力以及滑移扭矩进行仿真计算,并对结果进行分析。
1 橡胶扭振减振器结构
橡胶扭振减振器由惯量环、轮毂、橡胶圈组成。其中轮毂与发动机曲轴刚性连接,惯量环通过皮带与发动机前端附件相连,将发动机产生的扭矩传递到空调压缩机、水泵轮等附件装置。橡胶圈被机械力压入轮毂与惯量环的间隙中,利用橡胶圈的超弹性与粘弹性对发动机轴系进行减振。

图1 某型号橡胶扭振减振器
橡胶圈的形状分为中间凸出圆柱形(鼓型)和简单圆柱形(直筒型),已有研究表明[4],鼓形橡胶扭振减振器所能提供的压脱力与滑移扭矩比直筒型橡胶扭振减振器要大得多。文中研究鼓形长度、鼓形高度、橡胶圈压缩比对胶圈的压入力、压脱力及滑移扭矩的影响。

式中:δ表示橡胶圈的压缩比;C1表示压入轮毂和惯量环间隙前的橡胶圈厚度,大小为6.8mm;C2表示压入后的橡胶圈厚度,大小为3.81mm。某型号橡胶扭振减振器内部结构图如图2所示:鼓长A为25.65mm;鼓高B为3mm。

图2 某型号橡胶扭振减振器内部结构简图
2 有限元分析
2.1 橡胶超弹性本构模型
假设橡胶为连续变形体,工程中常用唯象理论来准确描述橡胶的变形[5],唯象模型的建立,关键在于构造合适的应变能密度函数。目前广泛应变能密度函数有2种,即基于应变不变量I1、I2、I3的应变能密度函数和基于主伸长比λ1、λ2、λ3的应变能密度函数[6]。应变不变量和主伸长比之间存在如式(2)所示的关系:

式中:主伸长比λi与主应变εi之间的关系为

根据式(2)~(3)可推导各本构模型的应变能密度函数。有限元软件中常用的本构模型有Mooney-Rivlin、Neo-Hookean以及Yeoh等。
在Abaqus中以一个适当的应变能密度函数对实验得到的应力-应变数据拟合,并将拟合得到的有关参数作为有限元分析的输入,进而预测要设计橡胶部件的力-位移曲线,其中Mooney-Rivlin模型最为常用,其应变能密度函数表达为[7]

式中:U为应变能密度;C10和C01为材料参数;I1和I2为第1~2阶应变不变量。
2.2 材料参数的确定
橡胶圈在压装的过程中,惯量环、轮毂以及导套相对于胶圈的变形很小,可忽略不计,所以这些金属件被设置为解析刚体,不必赋予材料属性。需要确定的是橡胶材料超弹性本构模型的参数C10和C01,可通过平面拉伸、单轴压缩实验得到[8]。当压缩比(该型号减振器为44%)确定时,不同硬度的橡胶C10和C01取值不同。压装前,硬度为65 HA的橡胶圈先放入 60°~80°的热水中加热3~5 min,使其变软,硬度约为60 HA,如图3所示。对橡胶圈进行压脱破坏和滑移破坏实验时,胶圈硬度为65 HA,C10和C01的值由胶圈供应商提供。

图3 橡胶圈加热前后的压力对比
基于Abaqus计算压入力时,输入材料参数C10为0.142 1,C01为0.287 6,计算压脱力和滑移扭矩时,输入材料参数C10为0.161 6,C01为0.324 6,橡胶密度为1.2-9t·mm-3。
2.3 质量放大系数的确定
基于Hypermesh对橡胶圈进行网格划分,其中网格大小设置为1.5×1.5,节点数为35 520,网格数为29 040。网格类型设置为C3D8R,一阶减缩积分单元,该单元存在沙漏问题,当系统伪应变能与内能之比不大于10%时,计算所得结果精度较高。
橡胶圈压入问题是一个准静态问题,当系统动能与内能之比在10%以内时,才能较准确地模拟准静态过程。在保证精度的前提下,引入质量放大系数可以有效地减少计算时间,当质量放大系数太大时,太多的动态因素对求解结果的精度影响过大,质量放大系数太小时,求解时间太长[4]。当质量放大系数分别为500、2 500和5 000时,系统伪应变能、系统动能与系统内能的比值曲线如图4所示:质量放大系数为2 500时,系统伪应变能与内能之比以及系统动能与内能之比均满足要求,所以质量放大系数取2 500。

图4 能量比值曲线图
2.4 摩擦系数的确定
基于Abaqus计算压入力、压脱力及滑移扭矩时,由于实际工况下接触条件复杂,摩擦系数难以确定,故暂均设为0.12,引进对比实验确定摩擦系数。假定摩擦初始系数为k0,仿真计算得到压入力F0,实测得到压入力F,摩擦系数k由式(5)确定[2]:

2.5 有限元求解
首先基于UG进行几何建模,将胶圈的模型导入Hypermesh,将其他部件的模型导入Abaqus;然后基于Hypermesh给胶圈划网格并导入到Abaqus中,赋予胶圈的材料属性,将轮毂、惯量环和压块设置为解析刚体,设置分析步、载荷步提交Job文件进行计算。
胶圈厚度为6.8mm,胶圈内径为142.3mm,胶圈高度为34.5mm,压缩比为44%,减振器鼓形高度为3.00mm,鼓形长度为25.65mm,计算出的压入力为34 548.3 N,压脱力为21 061.6 N,滑移扭矩为1 081.25 N·m。
3 对比实验
3.1 实验测量
减振器的扭转破环实验装置为沈阳机械制造厂制造的静扭试验机(图5)。实验前左臂与右臂平衡,两臂臂长均为1 m且两端均无配重。将样件固定在中间位置,左端无配重,右边加配重直至减振器滑移失效,此时右端配重155 kg,承受的扭矩峰值为1 519 N·m,且撤出配重后,胶圈无法恢复到初始状态。
图6所示为济南试验机厂制造的液压式万能试验机,用该装置对相同的另一个样件进行压脱破坏实验,压头处装附有传感器,传感器与显示控制器相连,可以测得压脱样件时压力为100.8 kN。
图7所示装置为合肥神舟液压机有限公司制造的液压机,用该液压机对橡胶圈进行压装实验,先将橡胶圈放入50°~80°的热水中加热3 min,将加热后的胶圈装在导套上,随导套压入表面附着压装油的零件里,压力表显示的读数为8.0 MPa,乘以胶圈上端面面积(受力面积),大小为26 059 N。

图5 扭转破坏实验

图6 压脱破坏实验

图7 橡胶圈的压装实验
3.2 摩擦系数的确定
按摩擦系数k0=0.12时,由Abaqus计算结果与实测结果如表1所示。由表1中数据对比可知:计算值与实测值差别太大,故摩擦系数均设为0.12时,不合理。由式(5)和表1中数据可得:压入力的摩擦系数应设为0.09,压脱力的摩擦系数设为0.57,滑移扭矩的摩擦系数设为0.17。将这3个摩擦系数分别输入到Abaqus中,对该型号减振器橡胶圈的压入力、压脱力和滑移扭矩进行再计算,得到结果如表1所示。由表1可知,用确定后的摩擦系数进行计算可以得到较理想的结果。

表1 摩擦系数计算值与实测值
4 实验设计
4.1 建立正交表
将影响胶圈失效的各因素分为3个不同的水平,如表2所示。根据正交实验法[9]可建立正交表L9如表3所示。
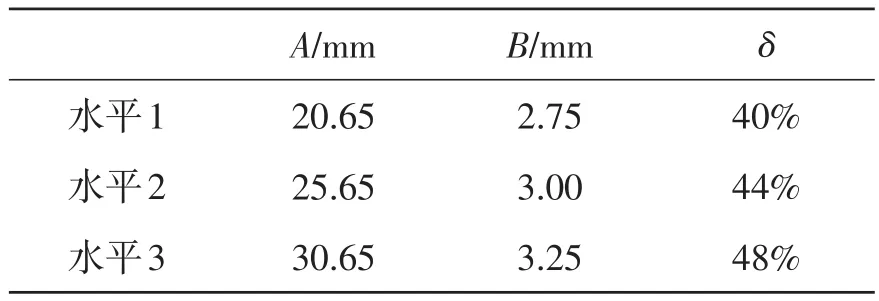
表2 各因素的水平

表3 正交表
该型号减振器胶圈的压入力为7~9 MPa,压脱力不小于45 kN,滑移扭矩不小于686 N·m。压块与橡胶圈的接触面积为3 185.2mm2,故压入力换算为22 296~28 667 N。
由表3中的计算结果可知:当鼓形长度为20.65mm,压缩比为40%,鼓形高度为2.75mm时,压入力峰值最小,表明橡胶圈在压装过程破损的可能性最小,此时压脱力和滑移扭矩均相对较小,但压脱力也达到了91.09 kN,滑移扭矩达到了1 201 N·m,均满足技术要求;当鼓形长度为20.65mm,压缩比为48%,鼓形高度为3.25mm时,压脱力最大,达到114 500 N,滑移扭矩也较大,达到1 702 Nm,满足要求,但此时的压入力太大,不宜压装;当鼓形长度为30.65mm,压缩比为48%,鼓形高度为3mm时,滑移转矩达到最大值,此时压脱力为110 570 N,但压入力达到最大29 501 N,且大于28 667 N,现有机械力压不进。
综上所述,有必要对正交表的计算结果进行极差分析,探究各因素对橡胶圈性能的影响程度。
4.2 极差分析
依据表3中相应的有限元计算结果进行基本极差分析,计算出相应的水平数、水平平均数和极差。其中
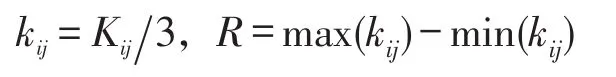
式中:R为极差;Kij为水平数;kij为水平平均数;i=1,2,3时分别表示某一因素的不同水平下的性能参数;j=1表示鼓形长度,j=2表示压缩比,j=3表示鼓形高度。
由表4可知:压缩比对压入力、压脱力和滑移扭矩的影响最为显著,但压缩比过大可能导致压装失败;对于压脱力,除压缩比以外,鼓形高度对其影响较大,通过适当增大鼓形高度来增大压脱力,以减小脱落失效的可能,对于该型号减振器,鼓形高度可取3.25mm,压脱力可达到105.67kN;对于滑移扭矩,在确定压缩比的情况下,可以通过增加鼓形长度以来增大。实验中鼓形长度取20.65mm时,滑移扭矩达到1455N·m,已满足技术要求。

表4 压入力、压脱力和滑移扭矩影响因素的极差计算
综上所述,当压缩比选定时,通过增大鼓长来增大滑移扭矩,通过增大鼓高来增大压脱力。
5 结论
基于Abaqus对某减振器的胶圈压入力、压脱力与滑移扭矩进行了试算,并通过实验对比确定摩擦系数;基于正交试验设计法,采用Abaqus仿真计算得到各因素的极差值,探讨计算结果并得出结论:1)压缩比对橡胶圈的性能影响最大;2)在压缩比选定的情况下,增大鼓长可增大橡胶圈的滑移扭矩;3)在压缩比选定的情况下,增大鼓高可增大橡胶圈的压脱力。
[1]王祺.内燃机轴系扭转振动[M].北京:国防工业出版社,1985.
[2]聂均.橡胶阻尼式扭振减振器结构性能研究[D].广州:华南理工大学,2015.
[3]上官文斌,聂均,魏玉明,等.橡胶扭振减振器滑移转矩计算方法研究[J].振动工程学报,2016(1):96-104.
[4]Belytschko T,Liu W-K,Kennedy J M.Hourglass Control in Linear and Nonlinear Problems[J].Compuer Method in Applied Mechanics and Engineering,1984(43):255-276.
[5]何平笙,杨海洋,朱平平.橡胶高弹性大形变的唯象理论[J].化学通报,2006(1):70-73.
[6]何小静,上官文斌.橡胶隔振器静态力-位移关系计算方法的研究[J].振动与冲击,2012,31(11):91-97.
[7]江丙云,孔祥宏,罗元元.ABAQUS工程实例[M].北京:人民邮电出版社,2014.
[8]杜晓泽.压入型橡胶扭振减振器性能计算与优化研究[D].广州:华南理工大学,2016.
[9]刘瑞江,张业旺,闻崇炜,等.正交试验设计和分析方法研究[J].实验技术与管理,2010,27(9):52-55.
Failure Analysis of Rubber Ring for Rubber Torsional Vibration Damper Based on Abaqus
Hu Hongfei1,Guo Yiming1,Xiao Zuyu2,Gan Xingang2
(1.School of Automotive Engineering,Hubei University of Automotive Technology,Shiyan 442002,China;2.Hubei Guang’ao Damper Manufacture Co.Ltd,Shiyan 442000,China)
The simulation trial calculation about the pressure,the pushing out force and the slip torque of rubber rings with different thickness was carried out based on Abaqus.Experiments were carried out to obtain the measured values,and the corrected coefficients of friction were determined.Based on or⁃thogonal experimental design,the influence of drum length,drum height and rubber ring compression ratio on pressure,pushing out force and slip torque were discussed.It is of guiding significance to solve the rubber ring failure in production practice.
finite element analysis;orthogonal test design;rubber ring failure
TQ336.4+1;U463.33+5
A
1008-5483(2017)04-0012-05
10.3969/j.issn.1008-5483.2017.04.003
2017-07-16
汽车动力传动与电子控制湖北省重点实验室开放基金项目(ZDK201106);十堰市科学技术研究与开发项目(20110272);湖北汽车工业学院硕士研究生创新基金资助项目(Y2016319)
胡鸿飞(1991-),男,湖北鄂州人,硕士生,从事汽车振动分析与控制方面的研究。E-mail:578678289@qq.com

