广义不变子空间的性质
李煜彦
广义不变子空间的性质
李煜彦
给出了广义不变子空间的概念,它是不变子空间的一个推广.文中讨论了广义不变子空间的交与直和,得到了判断广义不变子空间的一个方法,进而讨论了广义不变子空间与特征向量之间的关系.
向量空间;不变子空间;广义不变子空间;特征向量
不变子空间是线性变换中一个非常重要的概念,它在方程的求解、矩阵的特征根、矩阵的对角化、向量空间的直和分解等方面都有非常广泛的应用[1].近年来,有许多学者研究了不变子空间及其方法的应用.2008年,王波研究了不变子空间的性质[2];2014年,谭尚旺研究了线性变换不变子空间直和分解定理[3];2017年,张亚敏研究了广义的五阶KdV方程的不变子空间[4].这些结果都是在单个线性变换下考虑问题的.
本文以不变子空间的概念为基础,考虑在任意线性变换下研究相关问题,给出了广义不变子空间的定义,得到了广义不变子空间的性质和判断方法,讨论了广义不变子空间与特征向量之间的关系.设V是数域F上的向量空间,我们可以得到两个重要结论:①若W是V的子空间,{α1,α2,…,αr}是W的基.则W是V的广义不变子空间的充要条件是对任意σ∈S,σ(α1),σ(α2),…,σ(αr)在W中;②设dimV=n,若W是V的广义不变子空间,则对任意σ∈S,W必包含σ的一个特征向量.
1 预备知识
定义1[1]设σ是数域F上向量空间V的一个线性变换,W是V的一个子空间,若W中向量在σ下的像仍在W中,则称W是σ的一个不变子空间.
定义2[1]设V是数域F上的向量空间,σ∈L(V).若对F中的数λ,存在V的一个非零向量ξ,使得σ(ξ)=λξ,则称λ是线性变换σ的特征值,ξ称为σ的属于本征值λ的特征向量.
定义3 设S是数域F上的向量空间V的所有线性变换所成的集合,W是V的一个子空间,称W是V的广义不变子空间,如果对任意σ∈S,都有σ(W)⊆W.
显然,若W是V的广义不变子空间,则W是V的不变子空间,向量空间V本身和零子空间是V的广义不变子空间.
本文除特别说明外,FV均指的是数域F上的向量空间.S均指的是数域F上的向量空间V的所有线性变换所成的集合.
下面给出广义不变子空间若干性质和重要定理.
2 主要结果
性质1 设W1和W2是FV的广义不变子空间,则以下结论成立.
(1)W1⋂W2是V的广义不变子空间;
(2)W1⊕W2是V的广义不变子空间.
证明 (1)对任意σ∈S,因为W1和W2都是V的广义不变子空间,故有
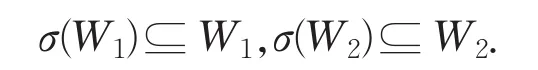
又因为σ(W1⋂W2)⊆σ(W1)且σ(W1⋂W2)⊆σ(W2),所以

从而W1⋂W2是V的广义不变子空间.
(2)容易得出σ(W1⊕W2)⊆σ(W1)⊕σ(W2)⊆W1⊕W2,即W1⊕W2是V的广义不变子空间.
根据性质1,我们容易得到下面的结论.
性质2 设W1,W2,…,Wn是FV的广义不变子空间,则以下结论成立.
下面结论将说明广义不变子空间关于子集具有遗传性质.
性质3 设V是数域F上的向量空间,X⊆Y⊆V.若X是Y的广义不变子空间,Y是V的广义不变子空间,则X是V的广义不变子空间.
证明 对任意σ∈S,有σ(Y)⊆Y.下证σ(X)⊆X.
令g=σ|Y∶Y→Y.则易知g是Y上的线性变换,且g∈S.由于X是Y上的广义不变子空间,因此g(X)⊆X,从而σ(X)=σ|Y(X)=g(X)⊆X.
下面给出一种判断广义不变子空间的方法.
定理1 设V是数域F上的向量空间,W是V的子空间,是W的基.则W是V的广义不变子空间的充要条件是对任意σ∈S,σ(α1),σ(α2),…,σ(αr)在W中.
证明 必要性.设W是V的广义不变子空间 ,则 对 任 意σ∈S,都 有σ(W)⊆W.而α1,α2,…,αr∈W,故σ(α1),σ(α2),…,σ(αr)∈W.
充分性.设ξ是W中的任意向量,则存在数域F的数k1,k2,…,kr使得
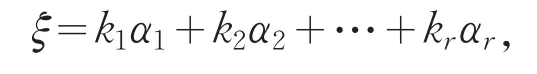
于是有
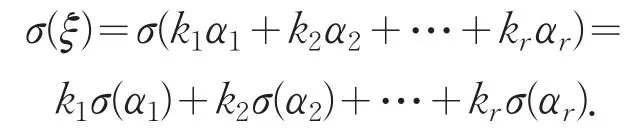
而由条件知σ(α1),σ(α2),…,σ(αr)都是W中的向量,所以σ(ξ)∈W.因此,W是V的广义不变子空间.
引理 1[5]设{α1,α2,…,αr} 是n维向量空间FV的一组线性无关的向量,那么总可以添加n+r个 向 量αr+1,…,αn,使α1,α2,…,αr,αr+1,…,αn作成V的一个基.
定理2 设V是复数域F上的向量空间,且dimV=n.若W是V的广义不变子空间,则任意σ∈S,W必包含σ的一个特征向量.
证明 令dimW=r.取W的一个基α1,α2,…,αr,由引理 1知,可以将W的基α1,α2,…,αr扩充为V的基α1,α2,…,αr,αr+1,…,αn.对任意σ∈S,由于有σ(W)∈W.所以有
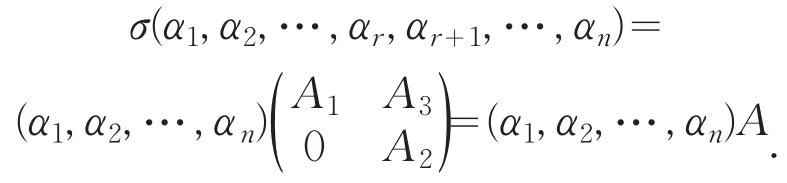

即X0是(λIn-A)X=0的非零解向量.
取α=(α1,α2,…,αr,αr+1,…,αn)X0=(α1,α2,…,αn)X01∈W,则
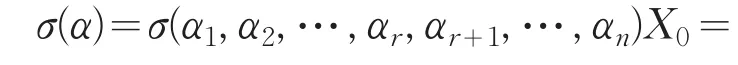

即α是σ的属于特征根λ的一个特征向量,从而结论得证.
3 结论
本文以不变子空间的概念为基础,给出了广义不变子空间的定义,讨论了广义不变子空间交、直和、遗传等性质和判断方法.得到了广义不变子空间关于交与直和都是封闭的,关于子集具有遗传性质,同时提出了广义不变子空间的一个充要条件.另外,文中还讨论了广义不变子空间与特征向量之间的关系,得出了对于数域F上n维向量空间V,若W是V的广义不变子空间,则任意σ∈S,W必包含σ的一个特征向量.
不变子空间已经有很广泛的应用,受到了许多作者的关注.关于本文定义的广义不变子空间是否有类似很好的应用将是我们后续关注的问题.
O151
A
1008-7974(2018)01-0038-03
10.13877/j.cnki.cn22-1284.2018.02.011
2017-06-14
陇南师范高等专科学校教学改革项目(JXGG201714);陇南师范高等专科学校校级科研项目(2016LSZK02002).
李煜彦,甘肃西和人,陇南师范高等专科学校数信学院讲师(甘肃 成县 742500).
[1]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京:高等教育出版社,2003.
[2]王波.不变子空间的一个性质[J].大学数学,2008,22(4):182-183.
[3]谭尚旺.线性变换不变子空间直和分解定理注[J].高等数学研究,2014,17(4):25-26.
[4]张亚敏.广义的五阶KdV方程的不变子空间[J].首都师范大学学报,2017,38(3):19-22.
[5]张禾瑞,郝鈵新.高等代数[M].北京:高等教育出版社,1983.
陈衍峰)

