基于邻居适应值的改进粒子群算法研究

李承启，龙圣杰，刘衍民*

（1.五邑大学数学与计算科学学院，广东江门529020；2.遵义师范学院数学学院，贵州遵义563006）

粒子群算法（PSO）[1]是Eberhart和Kennedy在1995年提出的，它是源于对鸟类觅食行为的模拟，具有操作简单、求解速度快等优点。与其它进化算法一样，PSO也存在容易早熟、局部寻优能力差等缺点。因此，为了提升算法的运行效率，许多学者提出了各种不同的改进策略，以克服算法存在的不足。例如，在种群拓扑结构改进领域，文献[2，3]提出了带收敛因子的局部版本的粒子群算法（CF-LPSO）和带收敛因子的全局版本的粒子群算法（CF-GPSO），文献[4]提出了局部版本的PSO（FIPS）。还有一些研究者对粒子的学习对象进行改进，如文献[5]提出了合作粒子群算法(CPSO)，文献[6]提出了全面学习粒子群算法（CLPSO），文献[7]提出了适应距离比例的粒子群算法（FDR-PSO）等，这些改进策略对于粒子跳出局部最优都有一定的效果，但是在求解精度和实现上仍有很大改进空间。

由于前面提到的改进算法存在一定的不足，本文提出了一种新的改进算法（NFPSO），该算法将种群分成三个子群，提取每个子群中最优个体，采用加权法构建具有全局代表性的最优个体。在检测函数的测试中，实验结果表明，相比基本粒子群算法NFPSO具有较好的性能，是对基本粒子群算法的一种有效改进。

1 基本粒子群算法

粒子群算法因其具有结构简单、操作方便的特点，在智能优化计算、图像识别与工程应用等领域得到广泛应用。

算法的进化方式如下：

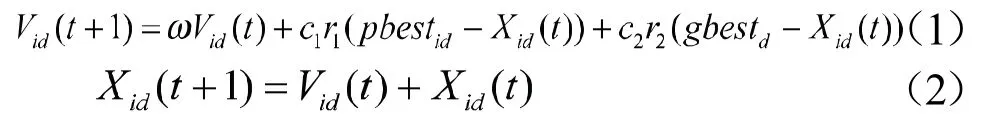
其中为i粒子的历史最

种群在进化过程中，粒子i的当前最好位置更新规则如下：

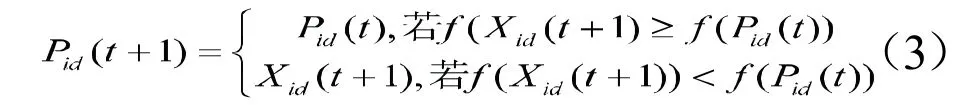
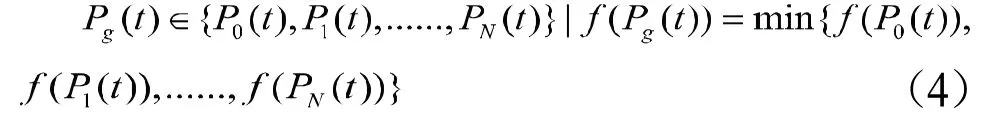
2 基于邻居适应值的改进算法

种群个体学习样本的选取是决定算法运行效率的主要因素之一[4]，而种群的拓扑结构（个体的邻居集合）决定了学习样本的选取。针对标准粒子群算法，根据种群邻居个体的不同，把标准粒子群算法分为全局版本（GPSO）和局部版本（LPSO），本文在LPSO基础上，采用把种群中每个个体的邻居平均分成三个子群，然后提取每个子群中运行最优的个体，对提取的个体按照适应值优劣进行排序，并按照个体的贡献比例，运用加权法来确定个体的学习样本。

在本文提出的改进策略中，对每个子群中对应的个体以适应值作为评价标准由优到劣进行排序。把适应值最优的个体所在的部分定义为最优俱乐部（最优运行个体用表示），适应值居中的定义为标准俱乐部（最优运行个体用表示），适应值最差的定义为最差俱乐部（最优运行个体用表示）。根据社会学理论所述：一个个体在社会中的地位和作用会随着他所处的集体不同而改变，例如：一个综合实力表现一般的人如果处在社会精英云集的集体里，他的表现可能会最差；在同类人构成的集体里，他的表现可能会较优；但在一个平庸的集体里，他的表现可能会最优。基于这一理论，将种群分成的三个子群分别类比于个体在不同环境中的表现，分别给予不同的子群不同的权重，多次仿真结果表明：三个子群的加权系数分别取0.7、0.2和0.1为最优的表现形式。综上，本文提出的速度更新公式为

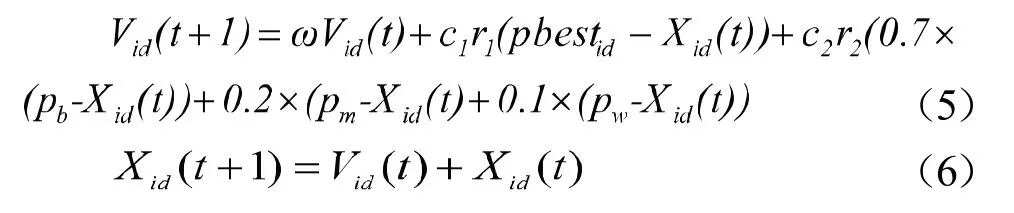
根据种群进化方程（5）和（6），NFPSO算法流程如下：

第二步：对于每个粒子，将当前的适应值与该粒子经历过的最好适应值进行比较，如果优于后者，则被当前的适应值替代；否则不变；

第四步：随机把种群邻居平均分成三个子群，确定每个子群中运行最优的个体，并将其按适应值从优到差进行排序；

第五步：根据式（5）（6）重新计算出每个粒子的速度和位置；

第六步：判断是否满足终止条件，若满足，输出最后的全局最优解和全局最优值，算法结束；若不满足，返回第二步。

3 实验结果和讨论

4.1 测试函数的选取

为测试算法的性能，选取国际上公认的六个测试函数来测试算法的运行效果，检测函数表达式如下：

（1）Sphere函数

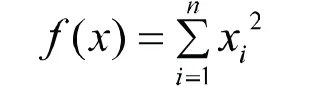
（2）Rosenbrock函数

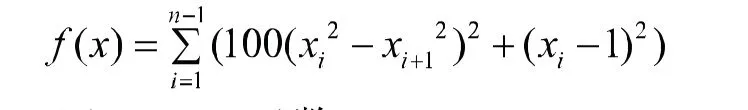
（3）Ackley函数

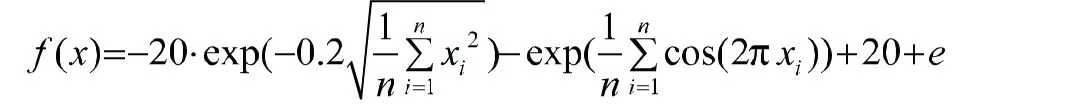
（4）Griewanks函数

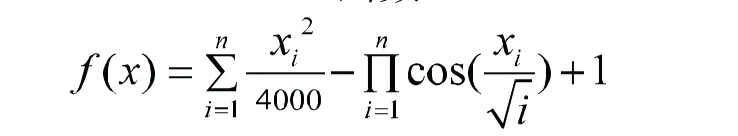
（5）Rastrigin函数

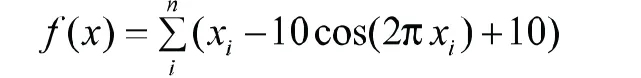
（6）Schewfel函数

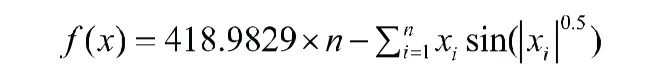
表1给出了六个检测函数的全局最优解、对应的全局最优值以及测试函数的搜索范围。

表1 测试函数的全局最优值和搜索范围

4.2 实验结果和讨论

实验设置如下：算法的种群规模为30，检测函数为30维，各种算法独立运行10次，计算次数均为3×104次，其它参数与算法提出时一致。选取国际上公认的经典改进算法CF-LPSO[2]、CF-GPSO[3]、FIPS[4]和CPSO[5]算法与本文提出的NFPSO算法进行比较。

图1给出了6个检测函数的收敛特征图，可以看出对于两个单峰函数而言，NFPSO收敛速度非常快，尤其是Sphere函数，NFPSO显著改善了运行结果，其它4种算法都陷入了局部最优。对于多峰函数而言，NFPSO算法不论在收敛速度和精度上相比其它算法也都表现出较好的运行结果。对于Rastrigin复杂多峰函数，NFPSO算法相比CF-LPSO、CFGPSO、FIPS算法表现出了极大的优势，它能有效地跳出局部最优解，预防早熟现象。

表2和表3分别给出算法在单峰和多峰检测函数下独立运行10次所得出的平均值和方差，最好结果用粗体表示。从表中可以看出，NFPSO所获结果都优于其它算法，与图1所得结论一致。这主要由于NFPSO算法采用了个体在群体中作用发挥机理，将种群中个体的信息充分利用，有效地提升了种群多样性。

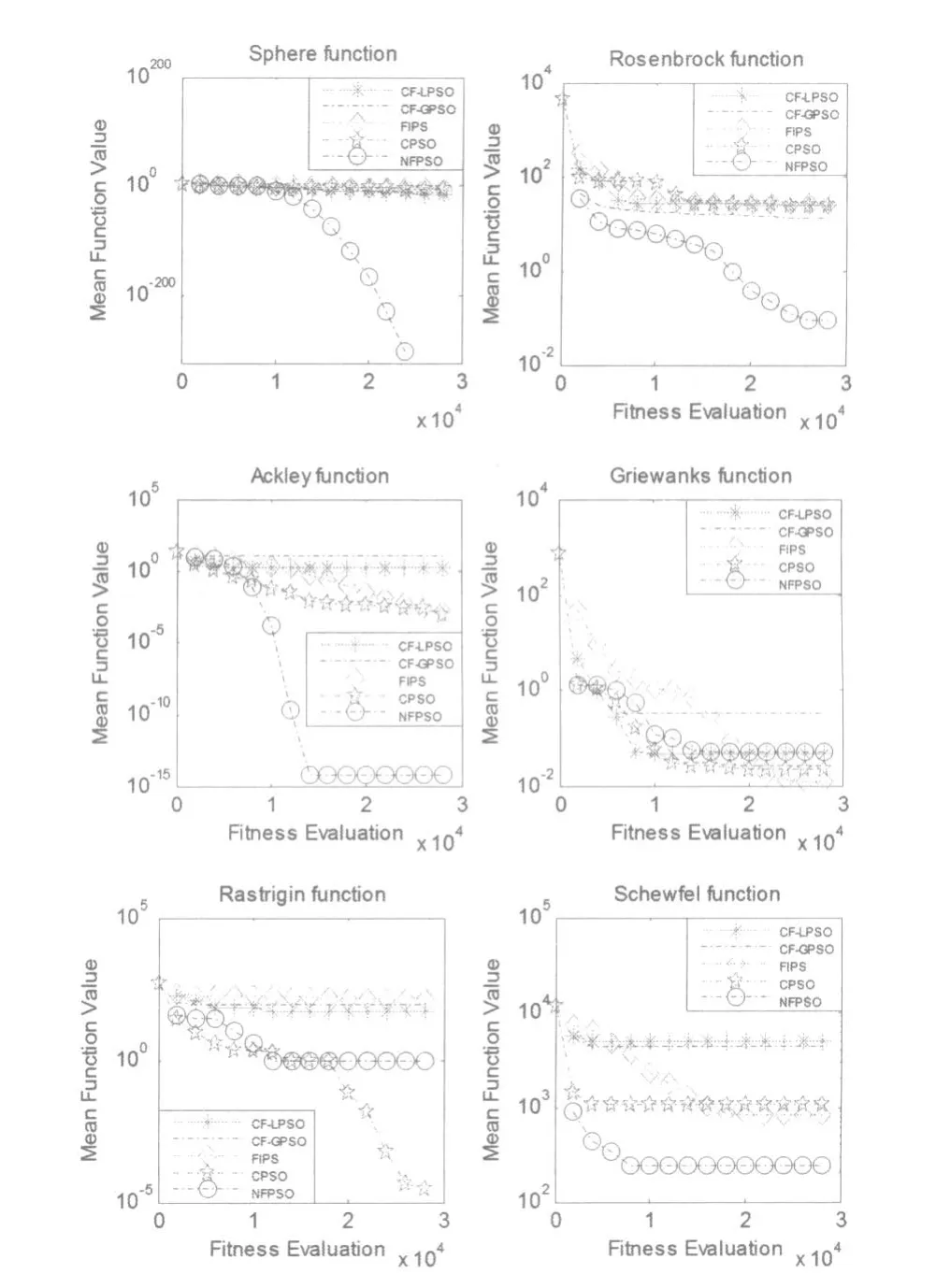
图1 检测函数的收敛特征图

表2 单峰函数在五个算法下运行10次的平均值及方差

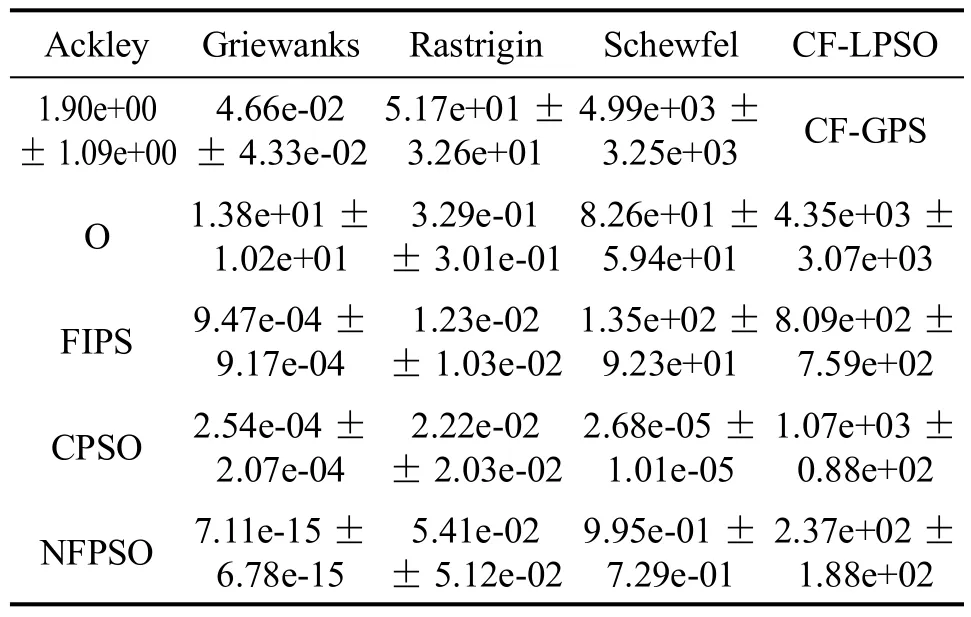
表3 多峰函数在五个算法下运行10次的平均值及方差

5 结论

本文提出了邻居适应值粒子群算法（NFPSO），借鉴了个体在集体中的作用发挥与其所处环境直接相关的社会学原理。以邻居适应值为依据，动态地构建种群最优粒子的拓扑结构，进而提升粒子之间的信息交流能力，增加种群多样性，此策略提高了算法的寻优能力。仿真实验表明，NFPSO不论是在单峰函数还是多峰函数上相比其它改进算法都表现了较优的结果。然而，粒子邻域的随机性对算法的稳定性有一定的影响，在今后的研究中将进行进一步的改进。

[1]Kennedy J,Eberhart R.Particle swarm optimization[C].IEEE International Conference on Neural Networks,Piscataway,1995.1942-1948.

[2]Kennedy J,Eberhart R.Population structure and particle swarm performance[C].Congress on Evolutionary Computation,Honolulu,2002.1671-1676.

[3]Clerc M,Kennedy J.The particle swarm-explosion,stability,and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1):58-73.

[4]Mendes R,kennedy J.The fully informed particle swarm:Simple,maybe better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210.

[5]Van dBF,Engelbrecht AP.A cooperative approach to particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2004,8(3):225-239.

[6]Peram T,Veeramachaneni K,Mohan CK.Fitness-distance-ratio based particle swarm optimization[J].Swarm Intelligence Symposium,2003,1019(1):174-181.

[7]Liang JJ,Qin AK,Suganthan PN,et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.