基于SDT和间接平差的中机身自动调姿精度分析

朱永国，张文博，刘春锋，赵爽

1.南昌航空大学 航空制造工程学院，南昌 330063 2.中航工业江西洪都航空工业集团有限责任公司，南昌 330024

基于SDT和间接平差的中机身自动调姿精度分析

朱永国1,*，张文博1，刘春锋2，赵爽2

1.南昌航空大学 航空制造工程学院，南昌 330063 2.中航工业江西洪都航空工业集团有限责任公司，南昌 330024

以4定位器式中机身调姿机构为研究对象，提出了一种飞机部件动态调姿精度的分析方法。首先，使用小位移旋量(Small Displacement Torsors, SDT)对定位器各关键公差建模，建立了定位器4层次误差SDT模型。其次，基于微分变换推导出定位器制造误差与中机身位姿误差之间的显式函数关系，给出了制造误差传递与累积系数矩阵。在此基础上，结合5次多项式轨迹规划方法，建立了单个定位器动态误差传递数学模型。然后，针对多定位器的误差耦合，综合运用间接平差法和加权最小二乘法，提出了多定位器球铰中心点动态误差耦合计算方法，并推导出了误差补偿量计算表达式。试验结果表明，依据该方法计算定位器驱动修正值，对调姿机构实施误差补偿，能较好地降低调姿误差，提高调姿部件的定位精度，为保证大部件对接装配协调准确度提供了有效途径。

飞机；装配；机身；小位移旋量(SDT)；间接平差；误差传递；误差耦合

依靠经纬仪测量，手工操作的传统飞机大部件对接装配方法已不能满足现代飞机高精度、高效、经济性等制造要求。需采用数字化对接装配系统，使飞机大部件对接装配朝着自动化和数字化的方向发展[1-3]。飞机大部件数字化对接装配系统主要由数控位置和姿态(以下简称位姿)调整机构、高精度数字化测量系统、运动控制系统等组成。其中，数控位姿调整机构往往采用三坐标POGO或定位器来实现大部件位姿的精确定位[4-7]。位姿能否精确定位既是大部件对接装配成功的关键因素，也是影响对接装配质量的重要因素。因此，需明晰调姿系统的误差源，建立位姿调整(以下简称调姿)机构的误差传递与累积计算表达式，并在装配过程实施动态误差补偿，以提高大部件的定位精度。

目前，已有不少学者对大部件调姿精度进行了研究。李晨等运用多体运动学理论对三坐标定位器式调姿机构的误差进行了分析，采用蒙特卡罗模拟法对误差分布进行了仿真[8]。郭飞燕等针对滚珠丝杠传动系统的安装误差，建立了柔性工装立柱单轴运动的定位误差模型[9]。郭志敏等研究了POGO柱受力变形引起的调姿误差[10]。朱永国等利用齐次变换矩阵分析了调姿机构各误差源与调姿部件位姿误差的关系[11-12]。以上研究成果为大部件调姿精度分析提供了基础，但仍存在以下3个亟待完善的方面：① 以往的研究没有顾及到调姿机构运动对调姿精度的影响，只进行了静态误差分析；② 以往的研究只关注于误差的传递与累积，没有提出驱动机构误差补偿的显式计算方法；③ 以往的研究仅分析了单个定位器对部件调姿精度的影响，没有给出多个定位器的耦合误差与调姿部件位姿误差之间的显式函数关系，也没有顾及到定位器球铰副中心坐标误差与调姿部件位姿误差的非线性强耦合关系。

小位移旋量(SDT)是表示刚体微小位移的6个运动分量所构成的矢量，Bourdet等首次将SDT引入到公差领域，并将其成功应用于不同类型的公差分析中[13-15]。文献[16-18]借助SDT对几何要素的形状、位置、方向和尺寸误差进行了定量的描述。工程实际中，调姿机构的制造误差均相比其几何尺寸是微小量，且调姿机构刚性大，调姿过程中受力变形相对于其几何尺寸也是微小量，因此，可以引入基于刚体假设的SDT公差建模方法进行调姿机构的误差分析。

基于以上分析，三坐标定位器式调姿机构已在飞机机身、机翼等大部件自动调姿中获得成功应用，为此，本文以中机身自动调姿机构为具体研究对象，其误差分析过程具有典型意义。引入SDT，用小位移旋量表示调姿机构制造误差；结合微分变换和5次多项式轨迹规划方法建立单个定位器动态误差的传递表达式；针对多个定位器误差耦合，引入测量学中的间接平差理论，将工艺接头球铰中心的位置坐标视为测量点，结合测量学

中的改正数计算式和加权最小二乘法，推导调姿机构动态误差耦合计算表达式，以获得装配部件位姿参数的波动区间和实时误差补偿量。

1 中机身调姿坐标系构建

图1和图2所示为三坐标定位器式中机身调姿机构，该调姿机构由4个三坐标定位器组成，利用钩头螺栓将中机身与调姿机构托架固连，定位接头与定位器通过球铰副连接，各定位器结构相同， 均由z向伸缩柱和滚珠丝杠驱动的x、y向导轨组成。中机身的位姿调整由4个定位器并联驱动。

图1 4定位器式中机身调姿机构
Fig.1Mechanism for fuselage posture adjustment with four positioners

为描述方便，建立图1和图2所示的坐标系：① 中机身坐标系Ofxfyfzf；② 定位接头坐标系Ojxjyjzj，4个定位接头坐标系分别记为Oj1xj1yj1zj1、Oj2xj2yj2zj2、Oj3xj3yj3zj3和Oj4xj4yj4zj4；③z向伸缩柱坐标系Opxpypzp，z向伸缩柱坐标系的坐标原点和定位接头坐标系的坐标原点重合，均为定位接头球铰中心点； ④x向导轨坐标系Os1xs1ys1zs1； ⑤y向导轨坐标系Os2xs2ys2zs2。各坐标系之间的位姿关系用φ、θ、ψ、x、y、z等6个参数表示。φ、θ、ψ是欧拉角，表示两坐标系之间的姿态关系，如果调姿机构没有制造误差，Opxpypzp、Os1xs1ys1zs1、Os2xs2ys2zs2之间的姿态角均为0°；x、y、z是坐标值，表示两坐标系之间的位置关系。

2 中机身自动调姿机构误差分析与建模

图3 定位器零部件形位误差
Fig.3 Shape and position errors of positioner parts

分析中机身自动调姿工艺可知，影响中机身调姿精度的因素主要包括：①调姿机构零部件制造误差；②数控驱动；③调姿机构零部件磨损；④温度变化引起的变形；⑤调姿机构受力变形。某型号飞机A类位姿测量点球形位置公差带的半径为0.3 mm[19]，与调姿精度要求相比：调姿机构零部件强度刚度均较大；装配车间内温度波动较小，温度影响可忽略不计；零部件磨损引起的误差也较小。为此，本文以调姿机构制造误差为分析对象，图3所示为影响中机身调姿精度的调姿机构零部件制造误差项。

2.1 基于SDT的调姿机构误差建模

利用基于SDT的公差建模方法，将调姿机构各零部件几何特征的形位、尺寸、装配间隙等误差统一用τ表示，τ=[dδ]T，其中，d=[dxdydz]为平动分量集，δ=[ΔθxΔθyΔθz]为转动分量集。各误差项传递时，将τ写成齐次变换矩阵：

2.2 基于SDT的零件几何特征误差累积

利用SDT的齐次变换矩阵形式，可得

(1)

(2)

(3)

结合式(1)～式(3)可知，零件装配位姿误差为零件上各几何特征SDT误差参数的对应项直接累加。

3 单个定位器误差传递与累积

3.1 定位接头

3.1.1 基于SDT的定位接头误差建模

如图3所示，将定位接头各误差项的SDT分别记为

(4)

式中：上标j表示定位接头；下标R表示圆度误差，PO表示位置度误差，RO表示圆跳动误差，TC表示球铰间隙误差，DT表示尺寸误差。

利用式(3)，可得定位接头各误差项SDT旋量参数累积表达式为

(5)

3.1.2 基于微分变换的定位接头误差传递

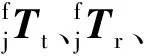
在定位接头坐标系Ojxjyjzj中，有

(6)

化简式(6)，可得

(7)

式中:

在中机身坐标系Ofxfyfzf中

(8)

整理式(8)，可得

(9)

式中:

(10)

(11)

式中:

经计算

(12)

(13)

(14)

式中：

化简式(14)，可得

(15)

(16)

3.2 z向伸缩柱和x、y向导轨

依据定位器接头误差分析方法进行z向伸缩柱和x、y向导轨的误差传递与累积。

3.2.1z向伸缩柱

将图3所示z向伸缩柱各误差项的SDT分别表示为

式中：上标p表示z向伸缩柱；下标C表示圆柱度误差；V表示垂直度误差；A表示同轴度误差。

再次利用式(3)，可得z向伸缩柱各误差项SDT旋量参数累积为

(17)

3.2.2x向导轨

将图3所示x向导轨各误差项的累积SDT分别表示为

式中：上标s1表示x向导轨；下标S表示直线度误差，F表示平面度误差，P表示平行度误差。

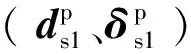
(18)

3.2.3y向导轨

将图3所示y向导轨各误差项的累积SDT分别表示为

式中：上标s2表示y向导轨。

(19)

3.3 5次多项式调姿轨迹规划

调姿过程中应避免启动和停止冲击，中机身起始位姿为标定值，终止位姿为对接装配目标位姿，因此，中机身调姿需满足以下约束条件：① 起始速度、终止速度分别为“0”；②起始加速度、终止加速度分别为“0”；③ 调姿初始位姿Xs=[xsyszsφsθsψs]T，调姿终止位姿Xe=[xeyezeφeθeψe]T。由调姿约束条件可知，调姿轨迹规划有6个约束，可用5次多项式实现调姿过程中的轨迹拟合：

f(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(20)

式中：a0～a5为多项式系数，t表示时间。利用约束条件求解式(20)，可得中机身运动轨迹方程为

(21)

式中：t0为调姿初始时间；te为调姿终止时间。

利用式(21)，可求得定位接头球心Pi的坐标为

Pi=RPfi+Po

(22)

式中：Pfi为定位接头球心在坐标系Ofxfyfzf中的坐标；Po为坐标系Ojxjyjzj相对于坐标系Ofxfyfzf的位置；R为旋转矩阵。

利用式(22)，可求得定位器各局部坐标系的位置坐标

(23)

3.4 单个定位器误差传递与累积

3.4.1 单个定位器4层次误差传递与累积

联立式(14)、式(17)～式(19)，可求得单个定位器各零部件制造误差引起的中机身调姿累积误差为

(24)

式中：df=[dfxdfydfz]、δf=[ΔθfxΔθfyΔθfz]分别为中机身位置误差和姿态误差。

由于伸缩柱坐标系Opxpypzp原点与定位接头坐标系Ojxjyjzj重合，经简单计算可得

(25)

(26)

3.4.2 误差分析

从式(26)可看出中机身位姿误差与单个定位器制造误差的关系为：①中机身姿态误差仅与各误差项的姿态误差相关，与位置误差无关，姿态误差的传递系数为各误差项所在坐标系相对于中机身部件坐标系的齐次变换矩阵；②中机身位置误差与各误差项的位置、姿态误差均有关。

由式(26)可知，df、δf均为各误差项SDT的线性累加。如果定位器为批量生产，各误差项为相互独立的正态分布，df、δf也应服从正态分布。则df、δf的数学期望E((df)T)、E((δf)T)计算表达式为

根据多个观测值线性函数的协方差阵计算方法[20]，df、δf的协方差阵D((df)T)、D((δf)T)计算表达式为

式中：D((dj)T)、D((dp)T)、D((ds1)T)、D((ds2)T)、D((δj)T)、D((δp)T)、D((δs1)T)、D((δs2)T)均为方差阵。

4 基于间接平差法的多定位器误差耦合

4.1 多定位器制造误差耦合

(27)

式中：

(28)

(29)

利用rR、Pt、Pr将式(29)进行扩展，得

(30)

图4 调姿实际位姿与调姿理论位姿关系模型
Fig.4Model for relationship between real posture and theoretical posture

4.2 基于间接平差法的多定位器耦合误差求解

利用式(30)可求得定位器制造误差耦合的间接平差方程为

(31)

式中：V为改正数；ΔP=Pr-Pt。

利用式(27)，可求得点pi的坐标误差ΔPi为

(32)

式中：Δθix、Δθiy、Δθiz为点pi引起的姿态误差；dti为点pi引起的位置误差。

利用式(32)，对ΔPi进行扩展，构建所有球铰中心点的坐标误差矩阵为

(33)

(34)

化简式(34)，得

(rR)TWV=0

(35)

(36)

由于各定位器均为独立制造，其制造安装精度指标均相同，可取W为单位阵，并将式(36)改写为

(37)

对式(37)求一阶、二阶导数，可求得中机身调姿速度误差和加速度误差。

4.3 定位器驱动误差反馈

(38)

利用式(38)进行定位器x、y、z方向驱动量的动态补偿，可提高装配部件的位姿精度。对式(38)求一阶、二阶导数，可求得定位器x方向、y方向和z方向的速度误差和加速度误差。

5 试 验

依据图1所示的调姿机构原理图，搭建图5所示的调姿试验机构，中机身用模拟件代替。该试验机构4个定位器x向、y向导轨行程均为500 mm，z向伸缩柱行程均为400 mm。表1所示为调姿机构制造误差检测值；表2所示为坐标系Ojxjyjzj相对坐标系Ofxfyfzf的位置；表3所示为坐标系Ojxjyjzj相对坐标系Ofxfyfzf的姿态角。表4所示为模拟件调姿试验初始位姿和目标位姿，各调姿试验模拟件的初始位姿、目标位姿均相同。试验总调姿时间均为200 s。试验过程中采用辅助测量杆对z向伸缩柱进行初始位置标定，利用测量靶球实现x、y向导轨初始位置的标定。利用型号为AT402的莱卡激光跟踪仪进行模拟件位姿测量。莱卡AT402激光跟踪仪的距离分辨率≤0.1 μm；绝对距离测量精度全量程范围内不超过10 μm；绝对距离重复性为5 μm。

图5 中机身调姿试验机构
Fig.5Experiment mechanism for fuselage posture adjustment

-

Continued

表2 坐标系Ojxjyjzj相对坐标系Ofxfyfzf的位置

表3 坐标系Ojxjyjzj相对坐标系Ofxfyfzf的姿态角

表4 调姿初始位姿和目标位姿Table 4 Initial and target postures of adjustment

5.1 试验机构驱动修正值计算

试验前，结合式(37)和式(38)，利用MATLAB计算出各定位器驱动误差，依据驱动误差得到如图6所示的各定位器驱动修正值。

由图6可明显看出，各定位器补偿量曲线具有很好的连续性、平缓、无突变，易于由运动控制系统实现。调姿过程中，各定位器的补偿量不是常量，随着调姿部件位姿的变换而改变；补偿量存在较大差异，补偿量范围为-0.675～0.814 mm。

图6 各定位器驱动修正值
Fig.6 Driving correction values of positioners

5.2 调姿试验

首先，对没有实施驱动补偿的调姿机构进行试验，利用激光跟踪仪测量不同调姿时刻中机身上4个测量靶球的坐标值，利用靶球的测量坐标值求解出中机身的位姿误差；依据位姿误差，绘制图7所示的位置和姿态误差曲线图。然后，依据图6所示的各定位器驱动修正值对试验机构各方向驱动量进行补偿，利用激光跟踪仪测量靶球的坐标值，求解不同调姿时刻中机身的位姿误差；依据位姿误差，绘制实施驱动补偿后的位姿误差曲线图，如图8所示。

由图8可看出，调姿过程中，试验机构的位姿误差是个动态值。位姿误差不仅与各定位器的制造精度、定位器的分布、定位器数量等存在强非线性耦合关系，还与运动轨迹存在耦合关系。对比试验位姿误差可知，无驱动修正时，位置误差波动范围为-0.163～0.222 mm，姿态角误差波动范围为-9.2×10-4～6.0×10-4(°)。实施驱动修正后，位置误差波动范围为-0.122～0.158 mm，姿态角误差波动范围为-4.8×10-4～3.1×10-4(°)。

利用图7和图8所示的调姿位姿误差试验数据，可得实施驱动修正前后的位姿误差的绝对平均误差、标准偏差和终点误差(表5)。

由表5可知，实施驱动修正后，到达目标位姿时，模拟件位置误差范围由修正前的-0.100～0.127 mm降低为-0.069～0.084 mm，角度误差范围由-5.6×10-4～1.22×104(°)降低为-8.5×10-5～1.22×10-4(°)，各位姿参数的绝对平均误差和标准差也均有较大幅度的减少。

综合以上试验结果可知，利用本文提出的装配部件动态调姿精度预测与驱动补偿量计算方法，能实现装配部件的调姿精度量化预测和误差补偿量的实时计算与反馈。调姿精度量化分析为数字化自动调姿机构的公差设计提供了理论依据，动态误差补偿为保证飞机大部件装配协调准确度提供了可行途径。

图7 无驱动补偿的中机身调姿误差
Fig.7 Errors of fuselage posture-adjusting without driving compensation

图8 驱动补偿后的中机身调姿误差
Fig.8 Errors of fuselage posture-adjusting with driving compensation

PositionandposeerrorPositionandposeFinalpositionerrorMeanabsoluteerrorStandarderrorx/mm-0．0670．0820．087y/mm0．1270．1710．185Withoutdrivingcompensationz/mm-0．1000．1320．142φ/(°)1．3×10-41．6×10-45．7×10-5θ/(°)4．7×10-45．4×10-41．9×10-4ψ/(°)-5．6×10-47．4×10-42．6×10-4x/mm-0．0640．0820．088y/mm0．0840．1100．124Withdrivingcompensationz/mm-0．0690．0870．094φ/(°)3．62×10-53．40×10-53．2×10-5θ/(°)1．22×10-41．26×10-41．0×10-4ψ/(°)-8．10×10-51．31×10-41．4×10-4

6 结 论

1) 针对飞机中机身自动调姿误差传递及其精度分析，综合运用小旋量理论、微变齐次变换、间接平差法和加权最小二乘法，提出了一套完整的中机身调姿精度预测与动态误差补偿计算方法。

2) 试验结果表明，利用提出的装配部件动态调姿精度预测与驱动补偿计算方法能实现装配部件的调姿精度量化预测和误差补偿量实时计算与反馈，依据误差补偿量对调姿机构实施误差补偿，能提高试验件的定位精度，减少调姿误差。

3) 飞机各大部件调姿机构的定位器数量、结构和误差项可能会存在差异，但本文提出的误差传递与耦合模型的推导过程具有较好的通用性，可以推广到具有不同数量定位器和不同误差项的飞机大部件调姿机构，也可应用于其他类似的并联机构。

致 谢

本文涉及的试验系统研制得到了南京航空航天大学黄翔教授及其带领团队的协助，特此致谢。

[1] 许国康. 大型飞机自动化装配技术[J]. 航空学报, 2008, 29(3): 734-740.

XU G K. Automatic assembly technology for large aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740 (in Chinese).

[2] 范玉青, 梅中义, 陶剑. 大型飞机数字化制造工程[M]. 北京: 航空工业出版社, 2011: 843-844.

FAN Y Q, MEI Z Y, TAO J. Digital manufacturing engineering of large aircraft[M]. Beijing: Aviation Industry Press, 2011: 843-844 (in Chinese).

[3] 林雪竹, 李丽娟, 曹国华, 等. 大部件对接iGPS高精度位姿测量优化设计[J]. 航空学报, 2015, 36 (4): 1299-1311.

LIN X Z, LI L J, CAO G H, et al. Optimal design based on iGPS high-precision posture measurement for large size component joining[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1299-1311 (in Chinese).

[4] 郭志敏, 蒋君侠, 柯映林. 基于POGO 柱三点支撑的飞机大部件调姿方法[J]. 航空学报, 2009, 30(7): 1320-1331.

GUO Z M, JIANG J X, KE Y L. Posture alignment for large aircraft parts based on three POGO sticks distributed support[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1320-1331 (in Chinese).

[5] 熊瑞斌, 黄浦缙, 柯映林. 一种适用于飞机装配的新型随动定位器[J]. 航空学报, 2009, 30(12): 2469-2475.

XIONG R B, HUANG P J, KE Y L. A new posture following and keeping fixture for aircraft assembly[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2469-2475 (in Chinese).

[6] ZHU Y G, HUANG X, FANG W, et al. Trajectory planning algorithm based on quaternion for 6 DOF aircraft wing automatic position and pose adjustment method[J]. Chinese Journal of Aeronautics, 2010, 23(6): 707-714.

[7] 雷沛, 郑联语. 面向飞机大部件调姿的PPPS机构球铰点中心位置闭环标定方法[J]. 航空学报, 2016, 37(10): 3186-3196.

LEI P, ZHENG L Y. Closed-loop calibration method of PPPS mechanism ball joint center position for posture adjustment of large aircraft component[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3186-3196 (in Chinese).

[8] 李晨, 方强, 李江雄. 基于三坐标定位器的大部件调姿机构误差分析[J]. 机电工程, 2010, 27(3): 6-12.

LI C, FANG Q, LI J X. Error analysis of 3-axis locator based pose adjustment mechanism[J]. Journal of Mechanical & Electrical Engineering, 2010, 27(3): 6-12 (in Chinese).

[9] 郭飞燕, 王仲奇, 康永刚, 等.飞机立柱式柔性工装定位误差分析与精度保障[J]. 计算机集成制造系统, 2013,19(8): 2036-2042.

GUO F Y, WANG Z Q, KANG Y G, et al. Error analysis and accuracy guarantee for column flexible tooling positioning of aircraft[J]. Computer Integrated Manufacturing Systems, 2013, 19(8): 2036-2042 (in Chinese).

[10] 郭志敏, 蒋君侠, 柯映林.一种精密三坐标POGO 柱设计与精度研究[J]. 浙江大学学报(工学版), 2009, 43(9): 1649-1654.

GUO Z M, JIANG J X, KE Y L. Design and accuracy for POGO stick with three axes[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(9): 1649-1654(in Chinese).

[11] 朱永国, 黄翔, 方伟, 等. 机身自动调姿方法及误差分析[J]. 南京航空航天大学学报, 2011, 43(2): 229-234.

ZHU Y G, HUANG X, FANG W, et al. Fuselage automatic position and pose adjustment method and its error analysis[J]. Journal of Nanjing University of Aeronautics &Astronautics, 2011, 43(2): 229-234 (in Chinese).

[12] 朱永国. 飞机大部件自动对接若干关键技术研究[D]. 南京: 南京航空航天大学, 2011: 35-39.

ZHU Y G. Research on some key techniques on aircraft large part automatic joining[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 35-39 (in Chinese).

[13] BOURDET P, MATHIEU L, LARTIGUE C, et al. The concept of the small displacement torsor in metrology[J]. Advanced Mathematical Tools in Metrology, 1996(40): 110-122.

[14] VILLENEUVE F, VIGNAT F. Advances in integrated design and manufacturing in mechanical engineering[M]. Berlin: Springer Netherlands, 2005: 189-200.

[15] ASANTE J N. A small displacement torsos model for tolerance analysis in a workpiece-fixture assembly[J]. Journal of Engineering Manufacture, 2009, 223(8): 1005-1020.

[16] 彭和平. 基于新一代GPS 框架的公差设计理论与方法研究[D]. 武汉: 华中科技大学, 2009: 31-34.

PENG H P. Study on theory and methodology of tolerance design within the framework of the new generation GPS standards system[D]. Wuhan: Huazhong University of Science and Technology, 2009: 31-34 (in Chinese).

[17] 茅健, 张恒, 曹衍龙. 基于SDT的平面尺寸公差模型研究及应用[J]. 工程设计学报, 2010, 17(5): 321-324.

MAO J, ZHANG H, CAO Y L. Research and application on model of size tolerance for plane based on SDT[J]. Journal of Engineering Design, 2010, 17(5): 321-324 (in Chinese).

[18] 吕程, 刘子建, 艾彦迪, 等. 多公差耦合装配结合面误差建模与公差优化设计[J]. 机械工程学报, 2015, 51(18): 108-118.

LÜ C, LIU Z J, AI Y D, et al. Assembly joint surface error modeling and tolerance optimization in the case of coupled tolerance[J]. Journal of Mechanical Engineering, 2015, 51(18): 108-118 (in Chinese).

[19] 刘楚辉. 飞机机身数字化对接装配中的翼身交点加工关键技术研究[D]. 杭州： 浙江大学, 2011: 99.

LIU C H. Study on key techniques of wing-fuselage joins machining in digital aircraft assembly[D].Hangzhou: Zhejiang University, 2011: 99 (in Chinese).

[20] 陶本藻，邱卫宁. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2009: 27-31, 106-111.

TAO B Z, QIU W N. Error theory and measurement adjustment basis[M]. Wuhan: Wuhan University Press, 2009: 27-31, 106-111 (in Chinese).

[21] 于成浩, 柯明. 基于激光跟踪仪的测量控制网测量精度分析[J]. 测绘科学, 2006, 31(3): 25-27.

YU C H, KE M. The measurement accuracy analysis of three dimensional control network based on laser tracker[J]. Science of Surveying and Mapping, 2006, 31(3): 25-27 (in Chinese).

AccuracyanalysisforautomaticaladjustmentofaircraftfuselageposturebasedonSDTandindirectadjustment

ZHUYongguo1,*,ZHANGWenbo1,LIUChunfeng2,ZHAOShuang2

1.SchoolofAeronauticalManufacturingEngineering,NanchangHangkongUniversity,Nanchang330063,China2.AVICJiangxiHongduAviationIndustryGroupCompanyLtd.,Nanchang330024,China

Thispaperdiscussesthemechanismforadjustingaircraftfuselagewithfourpositioners.Acalculationmethodisproposedtoanalyzedynamicposture-adjustingaccuracyofaircraftparts.TheSmallDisplacementTorsor(SDT)isusedtomodelthecriticaltolerancesofthepositioner,andtheSDTmodeloffourlevelerrorsisestablishedforthepositioner.Anexplicitfunctionrelationshipbetweenmanufacturingerrorsandfuselage’spostureerrorisbuiltbasedondifferentialtransformmethod,andthetransferandaccumulationcoefficientmatricesofmanufacturingerrorsarealsoderived.Amathematicalmodelfordynamicerrortransferofasinglepositionerisestablishedusingthefive-orderpolynomialtrajectoryplanningmethod.Then,toovercomeerrorcouplingofmulti-positioner,amethodforcalculatingdynamicerrorcouplingofmulti-positionersphericalcentersisproposedbyusingindirectadjustmentmethodandweightedleastsquaremethod,andtheexpressionforerrorcompensationisalsoderived.Thetestdatashowthatpositionandposeerrorscanbereduced,andposture-adjustingaccuracycanbeimprovedwithdrivingcompensationaccordingtotheproposedmethod,whichcanthusprovideaneffectivewaytoensureassemblecoordinationaccuracyoflargecomponents.

aircraft;assembly;fuselage;SmallDisplacementTorsor(SDT);indirectadjustment;errortransfer;errorcoupling

2017-04-05；

2017-05-10；

2017-07-03；Publishedonline2017-08-211928

URL：http://hkxb.buaa.edu.cn/CN/html/20171228.html

s：NationalNaturalScienceFoundationofChina(51565042)；FocusonResearchandDevelopmentPlansinJiangxiProvince(20161BBE53005，20171BBE50007)

.E-mailzhuyongguo_2003@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421301

2017-04-05；退修日期2017-05-10；录用日期2017-07-03；网络出版时间2017-08-211928

http://hkxb.buaa.edu.cn/CN/html/20171228.html

国家自然科学基金(51565042)； 江西省重点研发计划(20161BBE53005,20171BBE50007)

.E-mailzhuyongguo_2003@163.com

朱永国，张文博，刘春锋，等. 基于SDT和间接平差的中机身自动调姿精度分析J． 航空学报,2017,38(12):421301.ZHUYG,ZHAGNWB,LIUCF,etal.AccuracyanalysisforautomaticaladjustmentofaircraftfuselageposturebasedonSDTandindirectadjustmentJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):421301.

V262.4

A

1000-6893(2017)12-421301-14

李世秋)