基于改进排列熵的滚动轴承故障特征提取

陈祥龙 张兵志 冯辅周

摘要： 排列熵能够有效监测振动信号中的动力学突变，衡量振动信号的复杂度，在旋转机械状态监测中获得成功的应用。将排列熵应用于滚动轴承故障特征提取中，并针对排列熵对振动信号幅值不敏感，无法反映振动信号中局部能量分布差异的问题，利用滤波信号的归一化瞬时能量改进排列熵，提出一种基于改进排列熵的滚动轴承故障特征提取方法。仿真和试验数据分析结果表明，该方法能够有效识别滚动轴承共振频带，准确提取滚动轴承故障特征。

关键词： 故障诊断； 滚动轴承； 排列熵； 特征提取

中图分类号：TH165+.3； TH133.33 文献标志码： A 文章编号： 1004-4523（2018）05-0902-07

DOI：10.16385/j.cnki.issn.1004-4523.2018.05.021

引 言

滾动轴承是机械设备最容易发生失效的部位之一，及时有效地提取滚动轴承故障特征，确保机械设备连续可靠运行，避免因突发故障造成不必要的损失，是机械设备状态监测和故障诊断的研究重点[1]。当滚动轴承发生局部故障时，轴承会以一定的故障通过频率产生具有共振频率调制特征的循环瞬态故障冲击，在振动信号中表现出幅值调制特点。包络分析能够用于解调故障特征，但是如何准确识别滚动轴承共振频带是包络分析能够有效提取滚动轴承故障特征的关键[2]。

Antoni等[3-5]最早利用谱峭度（Spectral kurtosis）检测滚动轴承振动信号中的瞬态故障冲击成分，提出了峭度谱（Kurtogram），自适应确定共振频带并包络解调故障特征；张龙等[6]考虑瞬态冲击周期性发生的特点，提出了基于包络谱峰值因子和复Morlet小波滤波的最优共振频带确定方法；Tse等[7-8]定义了包络功率谱的稀疏度指标，结合Morlet小波滤波和遗传算法，确定滚动轴承的最优共振频带；Li等[9-10]提出多指标融合以及频谱细分合并确定滚动轴承最优共振频带，提高了最优共振频带识别的鲁棒性。

信息熵能够定量评价信息系统中的不确定性和复杂性，在机械设备状态监测和故障诊断领域获得广泛应用。秦娜等[11]提出基于小波信息熵等信息测度和样本熵等复杂性测度的高速列车转向架故障特征提取及退化状态评估方法；朱可恒等[12]提出了结合IMF包络样本熵与SVM的滚动轴承故障诊断方法；冯辅周等[13]提出基于排列熵的振动信号突变检测方法；郝旺身等[14]提出全矢数据融合和排列熵的齿轮故障特征提取方法；Antoni等[15]通过构造包络信息负熵和包络谱信息负熵，分别提出了包络负熵信息谱以及包络谱负熵信息谱，用于准确识别滚动轴承振动信号中的瞬态冲击特征。

综上所述，寻找一种或多种能够稳健识别振动信号中瞬态冲击成分的检测指标，确定滚动轴承共振频带，关系到滚动轴承故障特征提取的准确性和鲁棒性。利用排列熵检测振动信号动力学突变的特点，本文将排列熵应用于滚动轴承故障特征提取中，并针对排列熵对振动信号幅值不敏感，导致其无法准确反映滚动轴承振动信号在不同滤波频带中的能量分布问题，提出了一种基于滤波信号归一化瞬时能量的改进排列熵，用于稳健识别滚动轴承共振频带。

1 排列熵的基本原理

排列熵（Permutation Entropy，PE）是由Christoph Bandt等提出的一种基于时间序列各元素统计属性的平均熵参数，其利用一种较为简便的方法，衡量一维时间序列复杂度[16]。排列熵对信号的变化具有较高的敏感性，可以放大系统的弱变信号，并有效检测复杂系统的动力学突变。

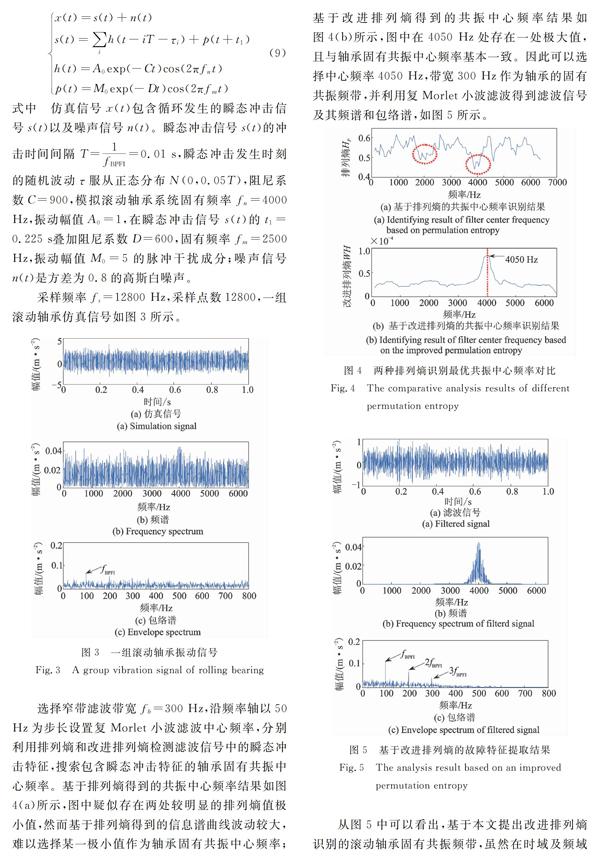
选择窄带滤波带宽fb=300 Hz，沿频率轴以50 Hz为步长设置复Morlet小波滤波中心频率，分别利用排列熵和改进排列熵检测滤波信号中的瞬态冲击特征，搜索包含瞬态冲击特征的轴承固有共振中心频率。基于排列熵得到的共振中心频率结果如图4（a）所示，图中疑似存在两处较明显的排列熵值极小值，然而基于排列熵得到的信息谱曲线波动较大，难以选择某一极小值作为轴承固有共振中心频率；基于改进排列熵得到的共振中心频率结果如图4（b）所示，图中在4050 Hz处存在一处极大值，且与轴承固有共振中心频率基本一致。因此可以选择中心频率4050 Hz，带宽300 Hz作为轴承的固有共振频带，并利用复Morlet小波滤波得到滤波信号及其频谱和包络谱，如图5所示。

从图5中可以看出，基于本文提出改进排列熵识别的滚动轴承固有共振频带，虽然在时域及频域上其窄带滤波信号瞬态冲击特征并不明显，但是在包络谱中能够清晰地识别出轴承内圈故障特征频率fBPFI=100 Hz及其三次谐频，因此改进排列熵能够有效提取出滚动轴承的故障特征，验证了本文提出方法的有效性。

3.2 滚动轴承试验台数据分析

采集某型变速箱滚动轴承振动数据，进一步验证本文提出方法的有效性，变速箱试验装置组成示意图如图6所示。

该变速箱输出轴支撑轴承为深沟球轴承，振动传感器安装在对应输出轴轴承径向光滑的机体位置。采用电火花加工法在新轴承的外圈设置尺寸微小的点状缺陷，模拟轴承外圈点蚀剥落故障，采集滚动轴承振动信号和输出轴转速信号。设置采样频率12 kHz，试验时的输出轴转频为fr=29.5 Hz，滚动轴承外圈故障特征频率fBPFO=106 Hz。一组滚动轴承外圈故障振动信号如图7所示。其中图7（a）是该信号的时域波形，图7（b）和（c）分别是该信号的频谱和平方包络谱。从图7（b）和（c）中很难直接提取出任何故障特征信息。

利用本文提出的方法分析该外圈故障振动信号，分析结果如图8所示。图8（a）为复Morlet小波带通滤波中心频率对应的改进排列熵值，图中具有最大改进排列熵值的共振中心频率位于fc=3450 Hz处，对应的滤波信号如图8（b）所示；滤波信号的包络分析结果如图8（c）所示，从图中能够清晰地提取出滚动轴承外圈故障振动信号的转频fr、故障特征频率fBPFO及其倍频。因此基于改进排列熵能够有效提取滚动轴承的故障特征频率，验证了该方法的有效性。

4 结 论

（1）排列熵虽然能够有效监测振动信号中的动力学突变，衡量振动信号的复杂度，定量反映振动信号的总体平均分布特征，但是对信号局部能量分布差异不够敏感，无法准确反映振动信号中的瞬态冲击特征；

（2）基于滤波信号归一化瞬时能量提出的改进排列熵，能够克服排列熵对振动信号幅值不敏感，无法准确反映信号中局部能量分布差异的问题，准确识别振动信号中的瞬态冲击特征；

（3）将改进排列熵与复Morlet小波滤波相结合，能够准确识别包含滚动轴承瞬态冲击特征的最优共振频带，准确提取出滚动轴承故障特征。

参考文献：

[1] Smith W A， Randall R B. Rolling element bearing diagnostics using the Case Western Reserve University data： A benchmark study[J]. Mechanical Systems and Signal Processing，2015， 64-65： 100—131.

[2] Chen X， Feng F， Zhang B. Weak fault feature extraction of rolling bearings based on an improved kurtogram[J]. Sensors，2016， 16（9）： 1482.

[3] Antoni J. The spectral kurtosis： a useful tool for characterising non-stationary signals[J]. Mechanical Systems and Signal Processing，2006， 20（2）： 282—307.

[4] Antoni J， Randall R B. The spectral kurtosis： application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing，2006， 20（2）： 308—331.

[5] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing，2007， 21（1）： 108—124.

[6] 張 龙， 熊国良， 黄文艺. 复小波共振解调频带优化方法和新指标[J]. 机械工程学报，2015，51（3）： 129-138.

Zhang Long， Xiong Guoliang， Huang Wenyi. New procedure and index for the parameter optimization of complex wavelet based resonance demodulation[J]. Journal of Mechanical Engineering， 2015， 51（3）： 129—138.

[7] Tse P W， Wang D. The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection[J]. Mechanical Systems and Signal Processing，2013， 40（2）： 520—544.

[8] Tse P W， Wang D. The design of a new sparsogram for fast bearing fault diagnosis： Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement-Parts 1 and 2”[J]. Mechanical Systems and Signal Processing，2013， 40（2）： 499—519.

[9] Li C， Liang M， Wang T. Criterion fusion for spectral segmentation and its application to optimal demodulation of bearing vibration signals[J]. Mechanical Systems and Signal Processing，2015， 64-65： 132—148.

[10]李 川，朱荣荣，杨 帅. 基于多指标模糊融合的滚动轴承诊断的最优频带解调方法[J]. 机械工程学报，2015，51（7）： 107—114.

Li Chuan，Zhu Rongrong，Yang Shuai.Optimal frequency band demodulation for fault diagnosis of rolling element bearings based on fuzzy fusion of multiple criteria[J].Journal of Mechanical Engineering， 2015，51 （7）： 107—114.

[11]秦 娜. 高速列车转向架故障的信息熵测度特征分析方法研究[D]. 成都：西南交通大学， 2014.

Qin Na. Research on high-speed train bogie fault data feature analysis method based on information entropy measurement[D].Chengdu： Southwest Jiaotong University， 2014.

[12]朱可恒. 滚动轴承振动信号特征提取及诊断方法研究[D]. 大连：大连理工大学， 2013.

Zhu Keheng. Research on vibration signal based on rolling element bearing feature extraction and fault diagnosis method[D]. Dalian： Dalian University of Technology， 2013.

[13]冯辅周，饶国强，司爱威，等. 排列熵算法研究及其在振动信号突变检测中的应用[J]. 振动工程学报，2012，25（2）： 221—224.

Feng Fuzhou， Rao Guoqiang， Si Aiwei， et al. Research and application of the arithmetic of PE in testing the sudden change of vibration signal[J]. Journal of Vibration Engineering，2012，25（2）：221—224.

[14]郝旺身，王洪明，董辛旻，等. 基于全矢排列熵的齿轮故障特征提取方法研究[J]. 振动与冲击，2016，（11）： 224—228.

Hao Wangshen， Wang Hongming， Dong Xinmin， et al. Gear fault feature extraction based on full vector permutation entropy[J]. Journal of Vibration and Shock，2016，（11）： 224—228.

[15]Antoni J. The infogram： Entropic evidence of the signature of repetitive transients[J]. Mechanical Systems and Signal Processing，2016， 74： 73—94.

[16]冯辅周，司爱威，江鹏程. 小波相关排列熵和HMM在故障预测中的应用[J]. 振动工程学报，2013，26（2）： 269—276.

Feng Fuzhou， Si Aiwei， Jiang Pengcheng. Application of wavelet correlation permutation entropy and hidden Markov model to fault prognostic[J]. Journal of Vibration Engineering，2013，26（2）： 269—276.

[17]Borghesani P， Pennacchi P， Chatterton S. The relationship between kurtosis-and envelope-based indexes for the diagnostic of rolling element bearings[J]. Mechanical Systems and Signal Processing，2014， 43（1-2）： 25—43.

[18]王宏超，陳 进，董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报，2013， 49（1）： 88—94.

Wang Hongchao， Chen Jin， Dong Guangming. Fault diagnosis method for rolling bearing′s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Mechanical Engineering，2013， 49（1）： 88—94.

Abstract： The permutation entropy can be used to efficiently detect the dynamic mutation and measure the complexity of 1-Dimensional time series. It has been successfully applied to condition detection of revolving machinery. This study proposes a method that applies permutation entropy into fault feature extraction of rolling bearings. However， permutation entropy is not sensitive to the amplitude of vibration signals and cannot reflect the difference of local energy distribution of vibration signals. Therefore， the permutation entropy is improved by utilizing the normalized instantaneous energy and a novel fault feature extraction method is proposed by the improved permutation entropy. The analysis results demonstrate that the proposed fault feature extraction method can effectively identity the resonant frequency band and extract fault features.

Key words： fault diagnosis； rolling bearing； permutation entropy； fault feature extraction

作者简介：陈祥龙（1989—），男，博士，讲师。电话：18801066586；E-mail： chenchendeplace@163.com

通讯作者：冯辅周（1971—），男，博士，教授，博士生导师。电话：（010）66718514；E-mail： fengfuzhou@tsinghua.org.cn