一般本构关系下岩石失稳破裂的尖点灾变模型研究
胥杰洋,赵忠虎,2,剌 珊
(1.兰州大学 土木工程与力学学院, 甘肃 兰州 730000; 2.亚利桑那大学 工程学院, 美国 图森 85721)
一般本构关系下岩石失稳破裂的尖点灾变模型研究
胥杰洋1,赵忠虎1,2,剌 珊1
(1.兰州大学 土木工程与力学学院, 甘肃 兰州 730000; 2.亚利桑那大学 工程学院, 美国 图森 85721)
针对岩石加载过程中的失稳现象,以灾变理论为工具,采用一般的岩石本构关系,研究了岩石试样在加载过程中的灾变失稳破坏机制。经过理论分析,建立了岩样单轴压缩失稳的尖点灾变模型,得出了岩样单轴压缩的失稳条件。推导了岩样失稳的尖点灾变模型在一般本构关系下的平衡方程、分歧点集、全位移参量、位移突跳、全位移等参量与能量突跳的表达式,进而分别讨论了这些参量随试验机的刚度和系统刚度比的变化状况。研究结果表明,试验机的刚度和系统的刚度比一定时,岩石加载系统的位移突跳值、全位移参量、全位移和能量突跳值均由系统的刚度比确定;位移突跳值与试验机的刚度、系统的刚度比成反比关系;岩石试样发生失稳破坏时的能量突跳值与试验机的刚度、系统的刚度比成反比关系。
灾变理论;尖点灾变模型;失稳破坏;刚度比
灾变理论自20世纪70年代初创立以来,就引起了诸多学者的兴趣。特别是80年代传入中国后,我国学者用其理论在岩石工程领域取得了较多的研究成果。唐春安等[1]通过岩石单轴加载系统并基于特殊的Weibull分布的本构方程,提出了岩石破裂失稳过程的尖点灾变模型,得到了岩石试样发生灾变时的位移突跳和能量突跳的表达式。在此基础上,陈忠辉等[2]以尖点灾变模型为工具,考虑形状参数为m的Weibull分布本构方程,获得了岩石试样在单轴压缩破坏时位移突跳的表达式,并使用绘图系统测试了岩石的位移变化,讨论了将灾变理论运用于岩石失稳研究的可行性。费鸿禄等[3]应用灾变理论研究了试验机-试样系统的失稳机制,推导出试样失稳的位移突跳表达式,最后通过试验验证了理论推导和实验结果的一致性。左宇军等[4]运用灾变理论研究了受静荷载作用的岩石因扰动而导致动态断裂的过程,建立了失稳的双尖点灾变模型,给出了岩石动态失稳的判据。潘岳等[5]进一步阐述了岩石系统在动力失稳时的总势能函数,探讨了失稳破裂起始点和终止点与能量释放的关系。杨小礼等[6]通过灾变理论研究了隧道底板的围岩稳定性,获得了分离围岩块体的破坏机制和轮廓,得到了一个可靠的破坏模型。刘学增等[7]建立了深部隧道失稳的尖点灾变模型,研究了黏弹性隧道围岩与衬砌在一定服务年限内各参数之间的关系。宋瑞刚等[8]研究了穿越断层破碎带的深埋隧道围岩的失稳现象,通过尖点灾变模型获得其失稳的力学判据。王心飞等[9]联合灾变理论与水致弱化函数建立了隧道围岩的尖点灾变模型,从系统刚度比、水致弱化系数比和几何力学参数等角度分析了隧道围岩的稳定性,并对隧道塌方提出了预防性措施。秦四清[10]通过建立岩质斜坡的尖点灾变模型,研究了斜坡的失稳过程。龙辉等[11]在本构关系中考虑了应变软化和水致弱化,用尖点灾变模型讨论了多种因素对滑坡孕育和触发的影响。孙强等[12]基于指数分布建立了平面滑动型斜坡的尖点灾变模型,研究了水的应力溶蚀效应导致的边坡失稳。周利杰等[13]建立了由降雨触发的岩质斜坡失稳的尖点灾变模型,研究分析了岩质斜坡失稳的力学机制。
从以上分析可以看出,很多学者主要应用尖点灾变模型研究了岩石力学的有关问题,是因为其控制变量有2个,临界面容易构成且比较直观,所以该模型是应用最广的灾变模型[14]。目前,研究者大都采用某种特定形式的本构关系,并将其代入到灾变理论中,然后完成研究工作。但是在这些工作中,采用特定的本构关系不能反映岩石单轴压缩过程中应力应变的一般性变化,同时会使得整个推导过程冗长繁琐,从而推导结果无法揭示某些带有普遍性的规律。为了弥补以上研究的不足,本文将从一般的岩石本构关系或者力与位移关系出发,研究岩石试样在单轴压缩状态下的灾变模型,建立岩石失稳破裂时的位移突跳和能量释放的表达式,以期加深灾变理论在岩石力学领域中的应用研究。
1 岩石系统位移变化情况及讨论
1.1 一般本构关系下岩石加载系统位移变化的理论推导
岩石单轴压缩系统由岩石试样和加载系统组成。在试验过程中,岩石试样与伺服机都会发生不同程度的变形[15]。由于两者刚度各不相同,所以最终变形量也不相同。因此将岩样和试验机分别简化为刚度系数不同的两段弹簧,并假设试验机的刚度为k。将岩样下端选为固定参考点,试验机上端受到大小为R的荷载作用,如图1所示。其中,整个系统的全位移为a,岩石试样的位移为u,则加载系统的位移为a-u。
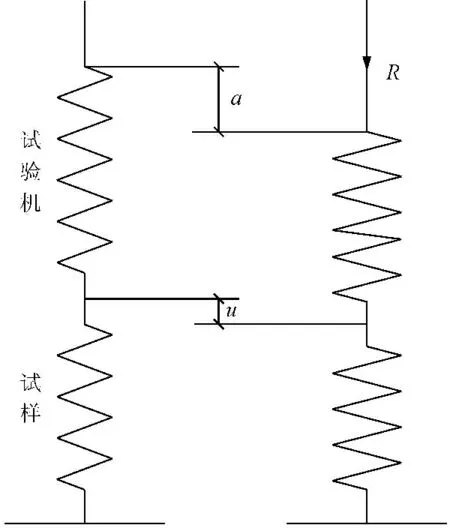
图1等效岩石单轴压缩系统
岩石典型的应力-应变曲线如图2所示,该曲线描述了岩石所满足的本构关系,可用式(1)的函数表达。
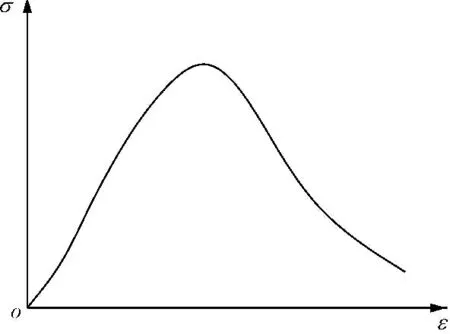
图2岩石本构关系
σ=g(ε)
(1)
对一定截面和长度的岩样,可将式(1)改变为一般的荷载与位移的关系
R=f(u)
(2)
式(2)中函数f随u的变化是先升后降,所以在下降段存在一拐点。将拐点处变形记为u1,所以有
f″(u1)=0
(3)
在这种条件下,系统的平衡方程(即平衡曲面方程)为
f(u)-k(a-u)=0
(4)
对图1所示的岩石单轴加载系统,首先建立该系统的势函数。该系统总势能V包括岩石应变能E和加载系统的弹性能W两部分,即
(5)
由V′=0可得出系统的平衡曲面方程为
V′=f(u)-k(a-u)=0
(6)
式(6)也是系统力的平衡条件。对式(6)微分可得系统歧点集所满足的条件,即
V″=f′(u)+k
(7)
根据平衡曲面处处光滑的性质,再对式(7)微分可得系统尖点灾变模型的尖点。令尖点处岩样的位移为u,在尖点处有V‴=0,即
V‴=f″(u)=0
(8)
结合式(3),可知在尖点处有
u=u1
(9)
即尖点处的位移值等于岩石本构曲线拐点处的位移值。
在尖点u1处将平衡曲面方程用泰勒级数展开为幂级数,并截取三次项,得到
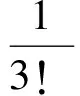
[f′(u1)+k](u-u1)+f(u1)-k(a-u1)=0
(10)
将式(3)代入式(10)可得
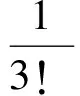
f(u1)-k(a-u1)=0
(11)
引入无量纲的状态变量[1]
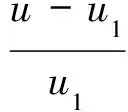
(12)
把式(12)代入式(11)中并经整理,得到一般本构方程下尖点灾变模型的平衡方程
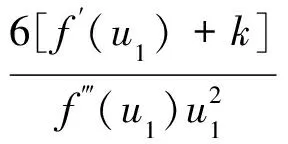
(13)
设
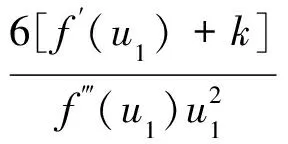
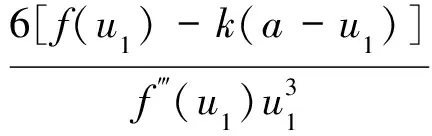
(14)
则式(13)可简化为
x3+Px+Q=0
(15)
式(15)也被称为尖点灾变模型的标准形式平衡方程。
在式(14)中,K定义为岩石试样和试验机组成岩石加载系统的刚度比[2],即
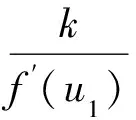
(16)
对于一般本构方程下,尖点灾变模型中状态变量x和控制变量P、Q的关系由式(15)给出。分歧点集由式(17)给出,其为一半立方抛物线。
4P3+27Q2=0
(17)
如果控制变量对(P、Q)在平面上缓慢变化,只要(P、Q)移动时不跨越分歧点集,系统的平衡点个数及其稳定性就不会发生变化。若(P、Q)移动时跨越分歧点集,系统性能将发生突变。
对于尖点灾变模型,其分歧点集(即式(17))只有在P≤0时才成立,即只有在P≤0时,控制变量对(P、Q)才能跨越分歧点集。所以由式(16)可知系统发生灾变的必要条件是系统刚度比K≤1。
设控制变量跨越分歧点集时系统的全位移参量为ξ,由文献[1]得
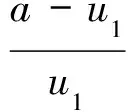
(18)
将式(14)代入分歧点集式(17)中,经演算可得
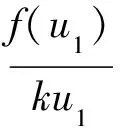
(19)
现确定分歧点集上状态变量的值。在分歧点集成立的条件下,当P=0时,方程式(15)有三重零根
x1=x2=x3=0
(20)
当P<0时,方程式(15)有三个实根,分别是
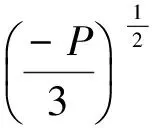
(21)
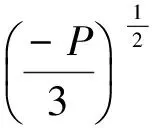
(22)
系统跨越分歧点集时,状态变量发生突跳,其值为

(23)
相对于失稳前后,岩样变形的突跳为

(24)
由全位移参量的公式,可知产生突跳时全位移的大小为
a=(1+ξ)u1=
(25)
1.2 一般本构关系下岩石加载系统位移变化的讨论
从系统刚度比,即式(16)可知,当试验机的刚度k下降时,系统的刚度比K也随之下降;当试验机的刚度k增大时,系统的刚度比K也增大,即试验机的刚度k与系统的刚度比K呈正相关。
综合分析式(16)、式(19)、式(24)、式(25)可知,试验机的刚度k和系统的刚度比K一定时,岩石加载系统的位移突跳值Δu、系统的全位移参量ξ和系统的全位移a均由系统的刚度比K确定,与其它因素无关。
当系统刚度发生变化时,如系统的刚度比K下降时,由式(19)、式(24)、式(25)并结合式(16)可发现,岩样失稳时的变形突跳值Δu不断增大,系统的全位移参数ξ和全位移a非单调变化。这意味着岩石系统的刚度降低时,岩样失稳破坏时所发生的位移突跳增加。
同理可得,随着岩石系统刚度比K的增加且满足K≤1的条件时,岩样失稳时的变形突跳值Δu不断减小,系统的全位移参数ξ和全位移a呈现非单调变化。此意味着系统的刚度增大时,岩样失稳破坏时所发生的位移突跳越小。
综合本节分析可知,岩石系统发生失稳破坏时,其位移突跳值Δu与系统的刚度比K成反比关系。
2 岩石系统能量变化情况及讨论
2.1 一般本构关系下岩石加载系统能量变化的理论推导
可以利用灾变前后系统的能量之差来估算失稳过程中释放的能量。将系统势函数式(5)在u=u1尖点处展开为泰勒级数,截取至四次项,得

(26)
将式(12)代入到式(26)中,可得

u1[f(u1)-k(a-u1)]x+b
(27)
其中

(28)
引入无量纲的能量变量U[1]
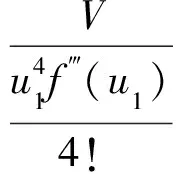
(29)
将式(27)代入到式(29)中,于是
U=x4+2Px2+4Qx+E
(30)
其中
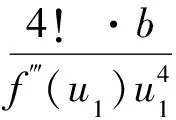
(31)
由式(30)可得系统突跳前后的能量差为
ΔU=U(x1)-U(x2)
(32)
将式(21)、式(22)的x1,x2值带入到式(32)中,可得
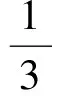
(33)
2.2 一般本构关系下岩石加载系统能量变化的讨论
从式(24)、式(25)、式(33)分析可知,当系统发生式(25)大小的全位移时,岩样将发生式(24)大小的位移突跳,突跳前后释放的能量差由式(33)计算得出。
当试验机的刚度k增大时,系统的刚度比K也增大,且满足K≤1的条件时,由式(33)知岩样失稳时的能量突跳值不断减小。意味着岩石系统的刚度增加时,岩样发生破坏时能量的释放变小。同理,随着系统的刚度比K变小,岩样失稳时的能量突跳不断增加。意味着岩石系统的刚度减小时,岩样发生破坏时能量的释放增加。由此可见岩石试样系统发生失稳破裂时能量的释放大小ΔU与试验机的刚度k和系统的刚度比K成反比关系。
3 一般本构关系下尖点灾变模型的验证
3.1 岩石试样本构关系的选取
在文献[2]中,陈忠辉等基于形状参数为m的Weibull分布本构方程,研究了岩石在单轴压缩下的失稳突跳,即假定岩石的本构方程为
(34)
其中,m是Weibull分布的形态参数,θ是标度参数,φ(ε)是概率密度函数,ε为岩样应变。
考虑式(34)和连续介质损伤力学本构关系,可将式(1)具体化为一本构关系
(35)
其中,σ为岩样的应力,E为岩样的弹性模量。
对截面面积为A、长度为L的岩石试样,可将式(35)转换为力R与位移u的关系,即分别在式(35)等号左右两端乘以A、L,在等号右端指数项m次幂内乘以L,得
(36)
因应力σ与岩样截面面积A乘积为岩样所受外力R,应变ε与岩样长度L乘积为岩样受力后的变形u,所以式(36)经整理后为
(37)
式(37)中,λ=EA/L为岩石试样的初始刚度,u0为一常数。
3.2 岩石加载系统刚度比、位移突跳及全位移参量的验证
将式(37)代入式(8)中,得
(38)
即
(39)
整理后可得岩石系统的尖点u1的表达式为
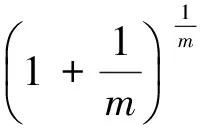
(40)
再将岩样力与位移的表达式(37)对位移u1分别求一阶、二阶和三阶导数,并将式(40)代入其中化简,可得
(41)
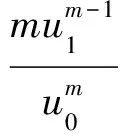
(42)
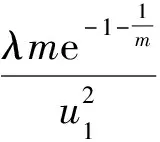
(43)
将式(41)代入式(16),可得Weibull分布本构模型下岩石系统的刚度比为
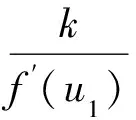
(44)
将式(37)、式(41)、式(43)代入式(19)并经整理,得到Weibull分布本构模型下岩石系统的全位移参量
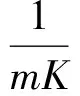
(45)
将式(41)、式(43)代入式(24)得出Weibull分布本构模型下岩样单轴压缩失稳过程中的位移突跳表达式为

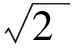
(46)
本文基于抽象的本构关系,经过理论分析得到了岩石单轴试验系统的刚度比(式(16))、全位移参量(式(19))和位移突跳值(式(24))。Weibull分布本构方程(式(35))是抽象本构关系的具体形式,将其代入到相应的表达式后,得到了基于Weibull分布本构方程的刚度比(式(44))、全位移参量(式(45))和位移突跳值(式(46))。通过对比本文式(44)、式(45)、式(46)与文献[2]的刚度比、全位移参量和位移突跳值可知,两者的理论推导结果一致。由此可以认为,本文基于岩石试样一般本构关系下所建立的尖点灾变模型和岩样破裂过程中的位移突跳值的正确性。同时表明将尖点灾变模型运用于岩石失稳破裂过程的研究是可行的,而且可以通过式(24)对岩样失稳的位移突跳量进行合理预测。
4 结 论
本文基于前人的研究,通过对岩石试样单轴压缩的分析,建立了岩石试样系统的尖点灾变模型,得到了以下结论:
(1) 以岩石在加载系统作用下破裂过程的失稳问题为背景,基于一般的本构关系σ=g(ε)和一般的力与位移关系R=f(u),推导得出了岩石在加载系统作用下失稳破坏的位移突跳和能量突跳表达式。
(2) 通过对失稳破坏的位移突跳和能量突跳表达式的讨论后认为,岩样失稳破坏时所发生的位移突跳值与试验机的刚度、系统的刚度比成反比;能量突跳值与试验机的刚度、系统的刚度比同样成反比。
(3) 将抽象的本构关系具体化为Weibull分布的本构关系,得到了Weibull分布下系统的刚度比、全位移参量和位移突跳值,该结果与文献[2]的研究结果一致。验证了本文所建模型的正确性,同时也说明了将尖点灾变理论运用于研究岩石失稳破裂的合理性。
[1] 唐春安,徐小荷.岩石破裂过程失稳的尖点灾变模型[J].岩石力学与工程学,1990,9(2):100-107.
[2] 陈忠辉,徐小荷,唐春安.单轴压缩下岩石失稳破裂的突跳[J].东北大学学报,1993,15(5):476-480.
[3] 费鸿禄,徐小荷,唐春安.突变理论研究单轴加载失稳与实验验证[J].中国有色金属学报,1995,4(3):52-57.
[4] 左宇军,李夕兵,赵国彦.受静载荷作用的岩石动态断裂的突变模型[J].煤炭学报,2004,29(6):654-658.
[5] 潘 岳,纪彩虹,李爱武.岩体系统动力失稳的总势能函数诠释[J].岩土工程学报,2007,29(6):831-836.
[6] Yang X L, Li Z W, Liu Z A, et al. Collapse analysis of tunnel floor in karst area based on hoek-brown rock media[J]. Journal of Central South University, 2017,24(4):957-966.
[7] 刘学增,朱保华,翟德元.深部隧道失稳的尖点灾变模型[J].山东科技大学学报(自然科学版),2000,19(1):38-40.
[8] 宋瑞刚,张顶立,文 明.穿越断层破碎带深埋隧道围岩失稳的突变理论分析[J].土木工程学报,2015,48(S1):289-292.
[9] 王心飞,王文广,刘新荣,等.隧道围岩失稳的突变理论分析[J].地下空间与工程学报,2008,4(3):1-5.
[10] 秦四清.斜坡失稳的突变模型与混沌机制[J].岩石力学与工程学报,2000,19(4):486-486.
[11] 龙 辉,秦四清,万志清.降雨触发滑坡的尖点突变模型[J].岩石力学与工程学报,2002,21(4):502-508.
[12] 孙 强,胡秀宏,王媛媛,等.两种应变软化介质组成的边坡失稳研究[J].岩土力学,2009,30(4):976-980.
[13] 周利杰,方 云.降雨作用下反倾岩质边坡尖点突变模型研究[J].水利与建筑工程学报,2008,6(4):130-131.
[14] 赵子都.一个新的数学分支——突变理论[J].数学通报,1986(8):35-39.
[15] 彭瑞东,谢和平,鞠 杨,等.试验机弹性储能对岩石力学性能测试的影响[J].力学与实践,2005,27(3):51-55.
CuspCatastrophicModelofRock’sFailureintheGeneralConstitutiveEquation
XU Jieyang1, ZHAO Zhonghu1,2, LA Shan1
(1.SchoolofCivilEngineeringandMechanics,LanzhouUniversity,Lanzhou,Gansu730000,China; 2.CollegeofEngineering,UniversityofArizona,Tucson,AZ85721,USA)
Focusing on the unstable failure of rock in the loading process, this paper analyzed the catastrophic failure mechanism of rock specimens with general equation in the process of uniaxial compression based on the catastrophe theory. Through theoretical analysis, the cusp catastrophe model of rock specimens under uniaxial compression is developed and the catastrophic condition is obtained based on the cusp catastrophe model. Parameters such as balance equation, bifurcation set, parameters of total displacement, displacement jumping, total displacement and the formula of energy jumping are deduced when the cusp catastrophic model of rock specimens is in the general constitutive equation. And then the changing situations of above parameters are discussed with the variation of machine’s stiffness and systematic rigidity ratio. The results show that sudden jump value of displacement, parameter of total displacement, total displacement and sudden jump value of energy of loading system are determined by systematic rigidity ratio when machine’s stiffness and systematic rigidity ratio are constant; The sudden jump value of displacement is inverse proportional to machine’s stiffness and systematic rigidity ratio; The sudden jump value of energy is inverse proportional to machine’s stiffness and systematic rigidity ratio.
catastrophetheory;cuspcatastrophemodel;unstablefailure;rigidityratio
10.3969/j.issn.1672-1144.2017.06.028
2017-08-01
2017-08-27
中央高校基本科研业务费专项资金项目(LZUJBKY-2016-110);国家留学基金项目(201606185039)
胥杰洋(1991—),男,四川江油人,硕士研究生,研究方向为岩石力学。E-mail: xujy15@lzu.edu.cn
TU43
A
1672—1144(2017)06—0143—05

