一种基于滑动带的土坡稳定分析方法研究

高 玮，冯 威，王家超，董俊全，杨 鑫，滕文馨，廖 慧

(河海大学 土木与交通学院， 江苏 南京 210098)

一种基于滑动带的土坡稳定分析方法研究

高 玮，冯 威，王家超，董俊全，杨 鑫，滕文馨，廖 慧

(河海大学 土木与交通学院， 江苏 南京 210098)

实际土坡发生失稳破坏时通常沿滑动带(剪切带)进行，而目前进行土坡稳定分析的方法几乎均仅考虑滑动面，这与实际有一定差别。为更符合滑坡的实际特点，提出了一种基于滑动带的土坡稳定分析新方法。该方法以黏性土坡为研究对象，基于土坡稳定分析的极限平衡条分法，认为土体沿滑动带发生的失稳破坏是以最危险滑动面为基础，多个非最危险滑动面共同作用的结果，通过模拟滑动带并筛选满足特定要求的滑动面，对其安全系数进行加权处理，计算最终安全系数。通过几个算例对新方法进行了验证，研究表明：新方法的计算结果较基于滑动面的Morgenstern-Price法结果、基于滑动面的Bishop法结果及有限元法结果偏小，偏于保守，新方法有一定合理性，可为以后的研究提供参考。

土坡；稳定分析；滑动带；滑动面；极限平衡条分法

目前，土坡稳定分析方法包括定性分析法、极限平衡法、极限分析法、数值分析法、非确定性分析法等[1-3]，这些方法大多认为土坡基于最危险滑动面失稳，而实际土坡发生失稳破坏通常沿滑动带(剪切带)进行[4-6]，因此，基于滑动带的土坡稳定分析方法更符合工程实际。

滑动带(剪切带)是指土坡发生失稳破坏时，由于土体材料的应变软化、土体的不均匀性、土体滑动时的扰动、拖曳、褶皱等因素，在坡体中形成的具有一定厚度的发生集中剪切变形的带状区域[5,7-8]。

目前，基于滑动带的土坡稳定分析方法尚无系统研究，相关研究主要集中在滑动带的形式、破坏机制及滑带土的物理力学性质等方面。Terzaghi K[9]最早阐述了边坡破坏的机理，揭示了滑动带产生的力学原理。陈明晓等[6,10]认为采用有限元法求解土坡稳定性时，以“某一幅值的等效塑性破坏区贯通”作为失稳判据，物理概念明确，且据此求得的塑性区可近似模拟滑动带[6]。Callari C等[11]针对滑动带形成过程中应变局部化问题做了相关研究。王宝亮等[4]对滑动带的破坏机制进行了相关研究。吴顺川等[12]采用数值分析方法，建立含软弱夹层的土坡分析模型，对滑动带的作用机制进行了研究。刘动[13]建立了一种土体应变局部化模型，运用数值分析手段对边坡沿滑动带的破坏过程进行了研究。Skempton A W[14]通过试验分析了土体抗剪强度在大剪切位移条件下的衰减规律，认为自然条件下滑动带土体能提供的抗剪强度接近其残余强度。陈祖煜等[2]考虑滑带土的强度衰减特性，指出运用条分法进行土坡稳定分析时，应根据相关原则采用残余强度指标进行计算。

由于对基于滑动带的土坡稳定分析方法缺少相关研究，本文以黏性土坡为研究对象，基于极限平衡条分法，建立滑动带与滑动面间的联系，进行相关研究并提出了一种基于滑动带的土坡稳定分析新方法。

1 基于滑动带的土坡稳定分析方法

1.1 相关定义

为便于描述，首先对相关概念进行定义：

(1) “较危险”滑动面：采用条分法得到的安全系数较小的若干滑动面。土坡沿这类滑动面发生失稳破坏的概率相对较高；“较危险”滑动面的具体数量视计算精度而定，其中必包括最危险滑动面。

(2) 合理“较危险”滑动面：“较危险”滑动面中滑面全部位于滑动带内的滑动面。滑动带有一定的分布区域，并非所有“较危险”滑动面均完全位于该区域内，如图1所示(其中粗实线为滑动带分布边界)；实际土坡发生失稳破坏在滑动带中发生，因此称这类滑动面为合理“较危险”滑动面。

(3) “亲近”距离：衡量某一合理“较危险”滑动面与最危险滑动面间的相对接近程度。本文认为“亲近”距离越小的滑动面与最危险滑动面越接近，在土坡失稳破坏中产生的影响越大，如图2所示(其中滑面1比滑面2更接近最危险滑面)。

1.2 研究思路及方法

本文认为，滑坡时土体沿滑动带发生失稳破坏的过程以最危险滑动面为基础。土体沿最危险滑动面滑动时，由于应变软化、扰动、拖曳等因素，使其可能选择在局部沿其他接近最危险滑动面的合理“较危险”滑动面滑动，且越接近最危险滑动面的滑动面被选中的概率越大。

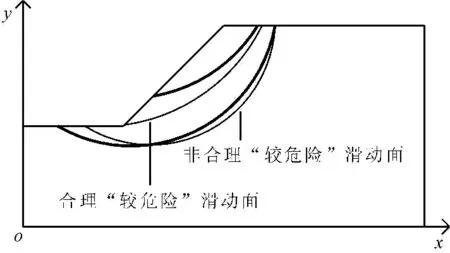
图1合理“较危险”滑动面示意图

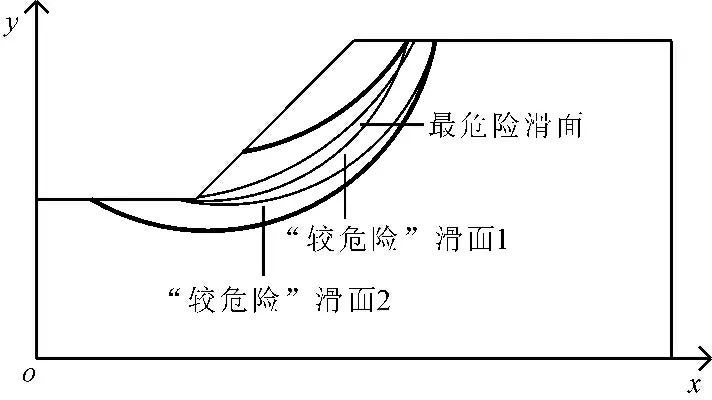
图2 “亲近”距离示意图

基于上述思路，具体研究方法如下：

对于一定坡形的土坡，首先确定滑动带的范围，由于文献[6]相关研究已经证明数值计算得到的“等效塑性破坏区”与实际滑动带比较接近，本次研究采用类似方法确定滑动带大致范围；然后根据条分法(本文研究了Janbu法、Morgenstern-Price法、Bishop法、Ordinary法)确定土坡若干“较危险”滑动面；根据“较危险”滑动面是否位于滑动带内筛选出合理“较危险”滑动面；最后，将筛选出的滑动面按“亲近”距离由小到大排序，并按正序选择合适数量(根据本文思路，排序靠后的滑动面对滑坡产生的影响相对较小，加权时可不作考虑)的合理“较危险”滑动面，对其安全系数加权处理得到最终安全系数。

1.3 合理“较危险”滑动面的筛选

图3所示土坡，粗实线表示滑动带的分布边界，坡形方程为

(1)

式中：x1、y1为坡脚横、纵坐标；x2、y2为坡肩横、纵坐标。

滑动带的分布边界和滑动面均假设为圆弧。滑动带的左侧和右侧边界对应方程分别为

Obnd1：(x-xbnd1)2+(y-ybnd1)2=Rbnd12

(2)

Obnd2：(x-xbnd2)2+(y-ybnd2)2=Rbnd22

(3)

式中：xbnd1、ybnd1为滑动带左侧边界圆弧的圆心横、纵坐标；Rbnd1为滑动带左侧边界圆弧的半径；xbnd2、ybnd2为滑动带右侧边界圆弧的圆心横、纵坐标；Rbnd2为滑动带右侧边界圆弧的半径。

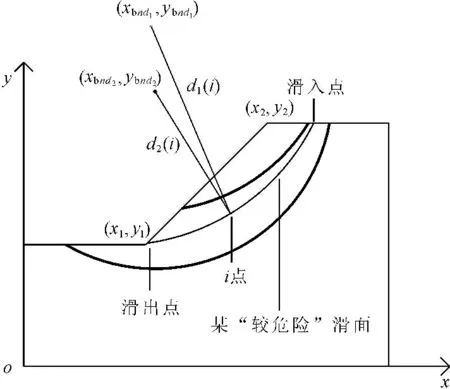
图3合理“较危险”滑动面的筛选示意图

设某个“较危险”滑动面对应的方程为

Odgr：(x-xdgr)2+(y-ydgr)2=Rdgr2

(4)

式中：xdgr、ydgr为“较危险”滑动面的圆心横、纵坐标；Rdgr为“较危险”滑动面的半径。

满足合理“较危险”滑动面的条件为：“较危险”滑动面上任意一点到圆心Obnd1的距离恒大于等于Rbnd1，到圆心Obnd2的距离恒小于等于Rbnd2。实际处理时，采用编程搜索的方法进行筛选，当滑动面上足够多的点满足要求时，即可确定为合理“较危险”滑动面。

将式(1)代入式(4)，可确定“较危险”滑动面的滑入点横坐标

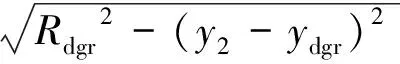
(5)

同理，滑出点横坐标为

(6)

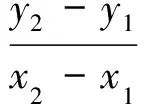
或

(7)

(滑出点位于坡脚情况)

设搜索点的数目为n，则该“较危险”滑动面上任意一点 的横坐标为

(8)

将式(8)代入式(4)，得到对应纵坐标(此为滑面圆心纵坐标高于坡肩纵坐标的情况)为

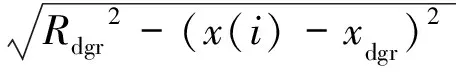
1≤i≤n

(9)

i点到圆心Obnd1及Obnd2的距离分别为

1≤i≤n

(10)

1≤i≤n

(11)

若该“较危险”滑动面上任意一点i均满足d1(i)≥Rbnd1且d2(i)≤Rbnd1(0≤i≤n)，则其为合理“较危险”滑动面，当划分精度n较大时，判别是准确的。这里记合理“较危险”滑动面为

(12)

式中：xr、yr为合理“较危险”滑动面的圆心横、纵坐标；Rr为合理“较危险”滑动面的半径。

1.4 “亲近”距离的确定

在最危险滑动面上，以滑入点为起点，滑出点为终点，将圆弧等分为n份，则等分点为n+1个，依次记为A1，A2，……,Ak，……An+1,对应坐标为

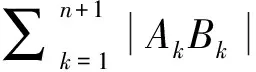
经试算，当n≥6时，n的取值对最终排序的结果影响不大，因此本文取n=8，如图4。最危险滑动面对应方程为

Om:(x-xm)2+(y-ym)2=Rm2

(13)

式中：xm、ym为最危险滑动面的圆心横、纵坐标；Rm为最危险滑动面的半径。

|A1B1|，|A9B9|，|A5B5|的求法类似，以|A1B1|为例，直线OmA1与圆Or相交，可得

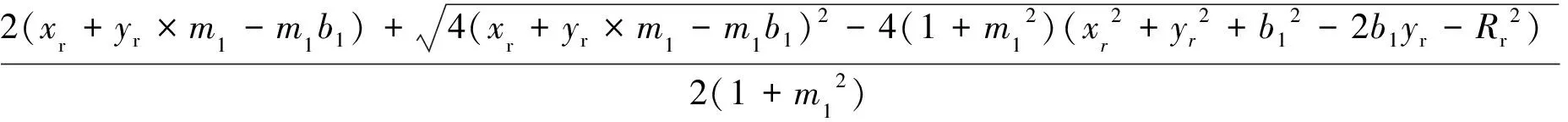
(14)

yB1=m1×χB1+b1

(15)

可得

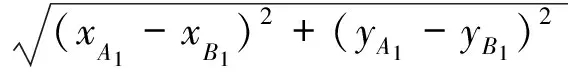
(16)

图4 “亲近”距离确定示意图

需要指出，由于不同土坡最危险滑动面位置不同，对于滑出点A9，其计算可能与式(14)及式(15)不符：若m9≤0，计算采用式(14)、式(15)；若m9≥0，需取直线OmA1与圆Or相交的横坐标较小值点；若m9为无穷，则xB9=xm。yB9视不同情况根据几何关系计算。

|A2B2|，|A3B3|，|A4B4|，|A6B6|，|A7B7|，|A8B8|求法类似，以|A3B3|为例，由于无法直接获得A3(xB3，yB3)，要确定OmA3直线方程，需先确定连线A1A5的中点

根据直线OmA3与圆Om及Or相交，采用式(14)及式(15)，可得出xA3，yA3，xB3，yB3，可得

(17)

需要指出，对于A8、B8，须采用与A9相同的方法进行判别，而对于其他点，一般情况下均可按式(14)及式(15)计算。

“亲近”距离为

(18)

1.5 权重的确定

本文将标准正态分布概率密度函数和λ=1的指数分布概率密度函数作为安全系数的权重分配函数，认为“亲近”距离越小的滑动面产生的影响越大，故权重的具体确定方法为：

(1) 标准正态分布概率密度函数：设需对h(h>0)个合理“较危险”滑动面对应的安全系数进行加权，见图5，该密度函数是关于y轴对称的函数，且当x≈3.1时，对应的函数值y≈0；将区间[0，3.1]划分成h个小区间，每个小区间长度s=3.1/h，将之前按“亲近”距离排序的安全系数以从小到大依次对应到划分的小区间(安全系数依次记为Fs1，Fs2，…，Fsj，…，Fsh)，如排序第1的安全系数Fs1对应区间(0,s]，排序第j的安全系数Fsj对应区间(j-1)s，js]则安全系数Fsj的权重βzj为标准正态分布概率密度函数在第j个小区间上的积分的两倍，为

(19)

(2)λ=1的指数分布概率密度函数如图6所示，处理思路与标准正态分布情况类似，该密度函数只在x轴正半轴有意义，且当x≈10.1时，对应的函数值y≈0，则每个小区间长度s=10.1/h，安全系数Fsj的权重βej为该概率密度函数在第j个小区间上的积分，为

(20)

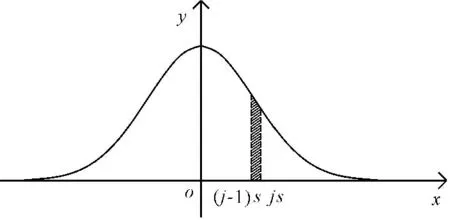
图5标准正态分布概率密度函数

图6的指数分布概率密度函数

2 案例分析

该案例摘自文献[15]，土坡参数为：坡高H=20 m，坡率m=1，黏聚力c=28.6 kPa，内摩擦角φ=20°，土重度γ=19.62 kN/m3；有限元法计算得到的安全系数为1.145，相应“等效塑性破坏区”如图7所示。

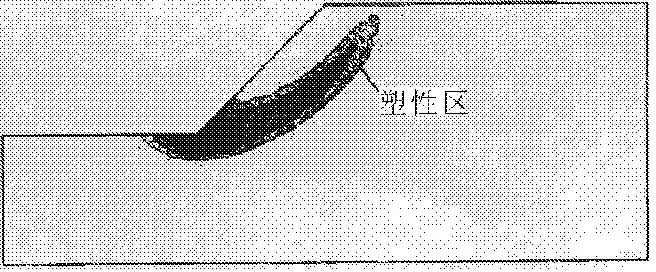
图7案例1“等效塑性破坏区”

土坡计算模型如图8(粗实线为滑动带边界)，模拟的滑动带左侧及右侧边界对应方程分别为

(x-20.9524)2+(y-55.8814)2=30.31082

(21)

(x-21.5744)2+(y-45.1899)2=29.13622

(22)

图8案例1坡形及滑动带边界示意图

首先采用Janbu法求解该土坡，共得到115个“较危险”滑动面，按安全系数由小到大排序，并进行合理“较危险”滑动面筛选，其中76个滑动面为合理“较危险”滑动面，39个滑动面不是合理“较危险”滑动面，部分滑动面信息见表1。在表1中，前9个滑动面均为合理“较危险”滑动面，其位置见图9。37号和42号滑动面不是合理“较危险”滑动面，位置见图10。

将得到的76个合理“较危险”滑动面按“亲近”距离由小到大进行排序，其中部分结果见表2。

表1 案例1部分滑动面信息

图9 案例1中1号到10号滑面示意图

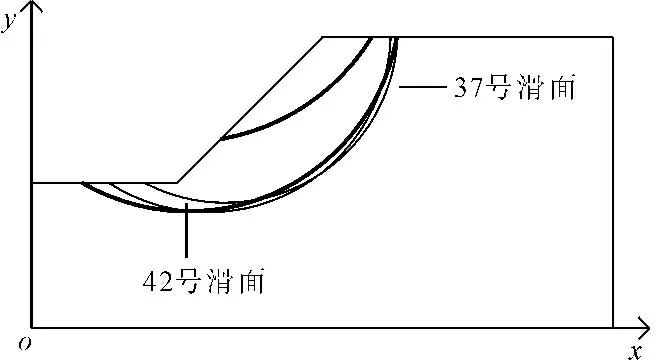
图10案例1中37号和42号滑面示意图

对排序好的安全系数分配权重并进行加权，为了研究具体对多少个滑动面进行加权能得到合理结果，本文分别选择前34个滑动面、前50个滑动面、前62个滑动面和全部76个滑动面加权进行研究，对前34个滑动面进行加权的权重分配部分结果见表3，加权得出最终结果见表4。

采用Morgenstern-Price法、Bishop法、Ordinary法的计算过程与Janbu法相同，最终结果见图11。

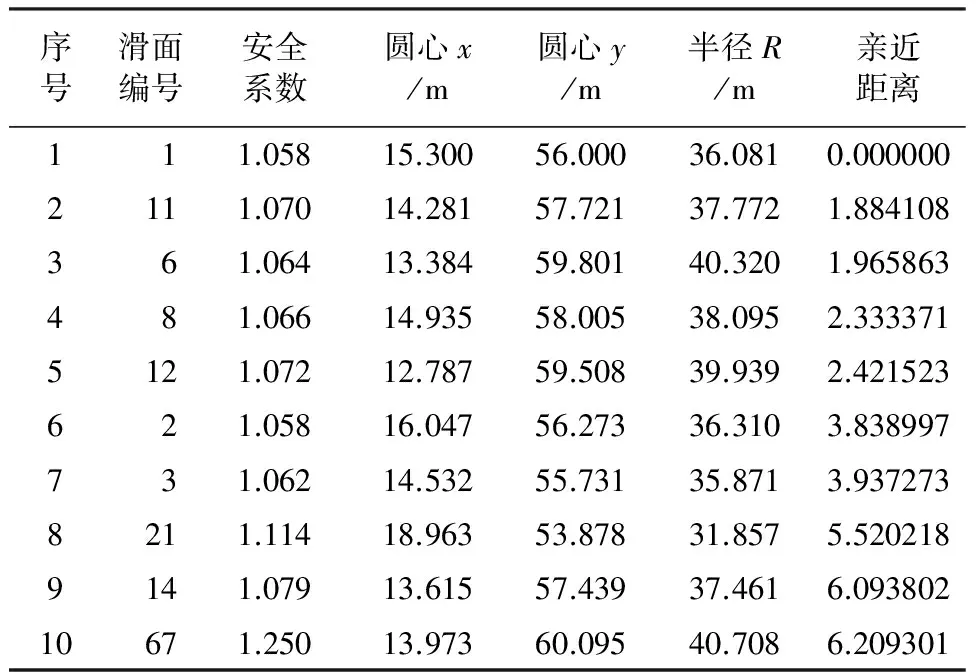
表2 案例1“亲近”距离排序部分结果

综合分析案例1的结果，可得如下结论：

(1) 当加权函数和加权滑动面数一定时，采用Janbu法处理得到的结果最小。如：采用指数分布概率密度函数对34个合理“较危险”滑动面进行加权，Janbu法、Morgenstern-Price法、Bishop法、Ordinary法处理的结果依次为1.0711、1.1025、1.1051、1.0782。

表3 案例1前34个滑动面权重分配部分结果

表4 案例1Janbu法加权计算结果

注：1.表中第一行“原结果”表示未经本文方法处理的基于滑动面的条分法计算结果，下同；2.表中第一行数字表示加权的滑面个数，如“正态34”表示按标准正态分布概率密度函数对排序后的前34个滑面进行加权，“指数34”表示按λ=1的指数分布概率密度函数对排序后的前34个滑面进行加权，下同。

图11案例1各方法结果折线图

(2) 当条分法和加权滑动面数一定时，采用指数分布概率密度函数处理的结果小于标准正态分布概率密度函数的结果。这是由于指数分布概率密度函数图像较陡，给排序靠前的滑面分配了较大的权重。如：采用Janbu法对34个合理“较危险”滑动面进行加权，指数分布概率密度函数和标准正态分布概率密度函数处理的结果分别为1.0711、1.0952。

(3) 当条分法和加权函数一定时，计算结果随加权滑面数增加而增大。如：采用Janbu法按指数分布概率密度函数处理，加权滑面数为34、50、62、76的结果依次为1.0711、1.0783、1.0834、1.0890。

(4) 采用Janbu法按指数分布概率密度函数对34个合理“较危险”滑动面进行加权的结果较基于滑动面的Morgenstern-Price法结果、基于滑动面的Bishop法结果和有限元法结果仍偏小，偏于保守。如：采用Janbu法的加权结果为1.0711(指数34)，较Morgenstern-Price法结果1.0900、Bishop法结果1.0930和有限元法结果1.145偏小。

综上，考虑到采用偏低的安全系数偏于保守，因此，采用Janbu法按指数分布概率密度函数对30个左右的合理“较危险”滑动面进行加权的结果更合理，该结果较基于滑动面的Morgenstern-Price法结果、基于滑动面的Bishop法结果和有限元法结果偏小，亦能说明结果的可靠性；由于Janbu法对土条的受力分析较为严谨，采用30个左右的滑动面进行加权也较充分地考虑了滑动带内多个合理“较危险”滑面的作用，新方法有一定的合理性。

3 结 论

(1) 本文考虑土坡滑坡时沿滑动带进行这一实际情况，认为土体沿滑动带发生的失稳破坏是以最危险滑动面为基础，多个非最危险滑动面共同作用的结果；通过模拟滑动带，筛选合理“较危险”滑动面，按“亲近”距离排序并加权得出土坡的安全系数。

(2) 采用Janbu法按指数分布概率密度函数对按“亲近”距离排序的前30个左右数量的合理“较危险”滑动面进行加权以得到最终安全系数，其结果较基于滑动面的Morgenstern-Price法结果、基于滑动面的Bishop法结果和有限元法结果偏小，偏于保守。

[1] 李广信.高等土力学[M].2版.北京：清华大学出版社，2016.

[2] 陈祖煜.土质边坡稳定分析[M].北京：中国水利水电出版社，2003.

[3] 董晓红，梁桂兰，许忠厚.边坡稳定分析方法综述及发展趋势研究[J].水利与建筑工程学报，2012，10(5)：100-106.

[4] 王宝亮，周 勇，陈洪凯.滑动带贯通破坏机制的研究[J].路基工程，2011(3)：169-175.

[5] 卢廷浩，刘祖德，等.高等土力学[M].北京：机械工业出版社，2005.

[6] 陈明晓.有限元强度折减法识别滑动带的例证[J].广州航海高等专科学校学报，2010，18(3)：26-30.

[7] 刘 军，刘育田.粘性土剪切带破坏研究[J].四川建筑科学研究，2014，40(1)：185-188.

[8] 李福林，彭芳乐，雷 亮，等.平面应变条件下砂土局部化剪切带的有限元模拟[J].岩石力学与工程学报，2010，29(4)：850-857.

[9] Terzaghi K. Soil Mechanics in Engineering Practice[M]. New York: Wiley, 1996.

[10] 吴伯建，朱珍德，顾祖军.有限元强度折减法进行土坡稳定分析的精度研究[J].水利与建筑工程学报，2013，11(1)：17-21.

[11] Callari C, Armero F. Finite element methods for the analysis of strong discontinuities in coupled poro-plastic media[J]. Computer Methods in Applied Mechanics and Engineering, 2002,191(39):4371-4400.

[12] 吴顺川，张晓平，刘 洋.基于颗粒元模拟的含软弱夹层类土质边坡变形破坏过程分析[J].岩土力学，2008，29(11)：2899-2904.

[13] 刘 动.基于滑带土剪切强度特性的边坡渐进性破坏研究[D].广州：暨南大学，2014.

[14] Skempton A W. Residual strength of clays in landslides, folded strata and the laboratory[J]. Geo-technique, 1985,35(1):3-18.

[15] 周资斌.基于极限平衡法和有限元法的边坡稳定分析研究[D].南京：河海大学，2004.

[16] 郑颖人，赵尚毅，宋雅坤.有限元强度折减法研究进展[J].后勤工程学院学报，2005,21(3)：1-6.

StabilityAnalysisMethodofSoilSlopeBasedonSlidingZone

GAO Wei, FENG Wei, WANG Jiachao, DONG Junquan, YANG Xin, TENG Wenxin, LIAO Hui

(CollegeofCivilAndTransportationEngineering,HohaiUniversity,Nanjing,Jiangsu210098,China)

The failure of a soil slope usually occurs along the sliding zone (shearing zone), but most of the slope stability analysis methods are based on the sliding surface, which is different from the actual situation. In order to accord with the actual characteristics of landslide, a new method is proposed to analyze the stability of soil slope based on sliding zone. Using the clay soil slope based on the traditional limit equilibrium methods, this paper considered that the failure of a soil slope along the sliding zone is based on the most dangerous sliding surface and influenced by a plurality of non-most dangerous sliding surfaces. Then by simulating the sliding zone and selecting the sliding surfaces which satisfy the specific requirements, the final factor of safety is calculated by weighting the factors of safety of the selected sliding surfaces. The new method is verified by several examples. The results show that the value from new method is smaller than that of the Morgenstern-Price method and the Bishop method based on the sliding surface, and also smaller than that of the finite element method, so the result is more conservative. Therefore the new method is reasonable and can provide a reference for future research.

soilslope;stabilityanalysis;slidingzone;slidingsurface;limitequilibriumslicemethod

10.3969/j.issn.1672-1144.2017.06.001

2017-06-21

2017-07-17

高 玮(1971—)，男，陕西富平人，博士后，教授，主要从事地质灾害防治、岩土力学与工程方面的工作。 E-mail:wgaowh@163.com

TU43

A

1672—1144(2017)06—0001—06