干旱地区非饱和路基土湿度的气候依赖性
李 聪,黄 科,王 峥
(1.招商局重庆交通科研设计院有限公司, 重庆 400067; 2.国家山区公路工程技术研究中心, 重庆 400067; 3.重庆交通大学 土木工程学院, 重庆 400074)
干旱地区非饱和路基土湿度的气候依赖性
李 聪1,2,黄 科3,王 峥3
(1.招商局重庆交通科研设计院有限公司, 重庆 400067; 2.国家山区公路工程技术研究中心, 重庆 400067; 3.重庆交通大学 土木工程学院, 重庆 400074)
为探究干旱地区非饱和路基土的湿度与气候的关系展开了相应研究。该项研究从干旱或半干旱地区在役路基现场湿度调研着手,揭示路基土含水率在深度方向的分布规律;选择基质吸力表征路基湿度,引入综合湿度指数ntmi表征气候因素。其次,根据不同土组,构建反映两者关联的ntmi简化模型,用以通过气候数据预估路基平衡湿度。最后,利用调研数据对模型进行了验证,研究结果表明:所构建的气候效应模型在定量表达气候因素对干旱地区路基湿度的影响方面比地下水位模型更为精确。
气候效应模型;路基平衡湿度;基质吸力;综合湿度指数TMI
干旱地区的公路路基土属于典型的非饱和土,例如,美国路面长期性能研究计划项目(Long Term Pavement Performance,LTPP)[1]对全美各地130余处路段进行了路基含水率调研,其中,砂类土路基近80处,黏质土路基近60处,结果表明,路基土的含水率主要分布于最佳含水率(Optimum Moisture Content,OMC)OMC~OMC+7%范围内,远未达到饱和。另一方面,干旱或半干旱地区的区域气候特征对路基土的湿度状态影响很大,Russam K等[2]建立了砂土等土类的基质吸力与气候参量之间的关系曲线,用以预估路基湿度。Aitchison G D等[3]改进了上述模型,并形成了多类路基土的可用于指导设计的吸力曲线,不过,这种曲线仅适用于地下水位较深的干旱、半干旱地区(年降雨量小于等于254 mm)。曹长伟[4]通过研究发现,当地下水位很低,路基顶面以下80 cm深度范围,即路基工作区的湿度受地下毛细水上升润湿的影响很小,而受气候条件的影响却很大。因此,通过构建合适的指标表征气候因素,进而建立气候对路基土非饱和特性的定量影响关系,再进一步预估路基服役期实际所处含水率,这是本文研究的总体思路。
1 路基平衡湿度及其表征指标
1.1 路基平衡湿度的定义
公路路基在建造完成初期,含水率通常在OMC附近波动,处于非饱和状态。而在其运营期间,外部雨水入渗、内部滞水渗流等原因,造成路基含水率发生变化,并于3 a~5 a后趋于稳定(如图1所示)。此时,路基湿度与周围环境达到平衡状态,称为平衡湿度,也即平衡含水率EMC[5]。
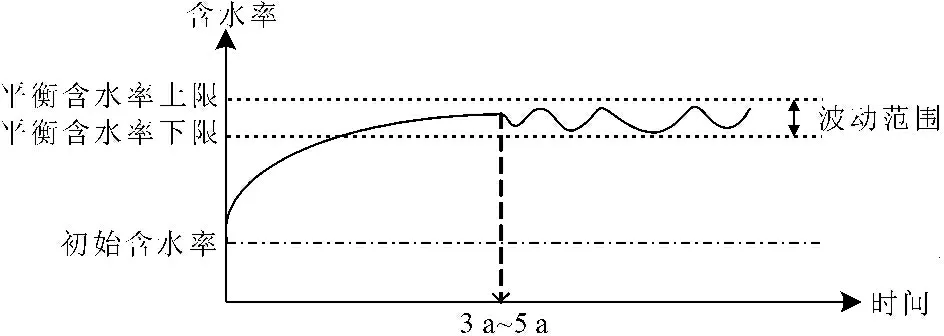
图1路基湿度演化大致规律
1.2 常规表征指标
湿度的评价指标通常来讲,分为绝对指标与相对指标。绝对指标使用最广泛的为质量含水率w,而相对指标主要为饱和度Sr与体积含水率θw。三个指标之间存在一定的关系:
(1)Sr与w之间的关系

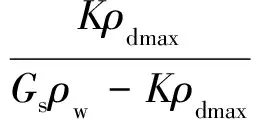
(1)
(2)θw与w之间的关系

(2)
(3)θw与Sr之间的关系

(3)
(4) 土体孔隙比e的计算公式
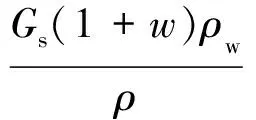

(4)
式中:ρs为土粒密度,g/cm3;ρw为4℃时水的密度,ρw=1 g/cm3;Gs为土粒比重,即土粒相对密度,Gs=ρs/ρw;ρd为土的干密度,g/cm3;ρdmax为一定压实功率下土的最大干密度,g/cm3;K为压实度,K=ρd/ρdmax。
在Gs、ρd已知的前提下,只需测得w、Sr和θw中的其中一个,就可通过上述公式推求其它两个。一般而言,土体体积随着含水率绝对数量变化而产生相应的变化,这就意味着即使w不变,Sr、θw也会发生变化。因而表征湿度时,需要考虑绝对含水率大小和土体密实程度两个因素,Sr、θw均包含了两个方面的影响。
1.3 基质吸力
严格来讲,土体吸力可分为渗透吸力hos与基质吸力hs[6],考虑到hos在其值的数量级上以及对土体工程性质的影响程度上,均小于hs,所以本文所指基质吸力可简称为吸力。土-水特征曲线(Soil-Water Characteristic Curve,简称SWCC)则是表征土体吸力与含水率之间关系的曲线[7]。该曲线反映了在非饱和状态下,土中水的能态随其数量的变化趋势,如图2所示。

图2土体的典型SWCC[7]
鉴于基质吸力与土体模量、抗剪强度指标等物理力学参数具有较好的相关性[8],本文采用此指标表征服役路基湿度状态。
2 路基湿度调研与大气降水入渗机理
2.1 路基湿度现场调研
本文选择新疆、重庆、四川等干旱(或半干旱)地区不同等级公路共10余个路段进行了现场调研,调研路段均通车3 a以上。调研测得的路基湿度为平衡湿度。
路基湿度现场调研项目主要包括:(1) 调研公路相关情况项目,如路段位置,所在地气象、水文资料等;(2) 现场测量项目;(3) 室内物性参数试验项目。现场调研路段的基本情况以及路基土的实测质量含水率w与实测基质吸力hs的结果如表1所示,调研点所取土样通过室内试验得到的物性参数,例如塑性指数IP、细粒含量P200等如表1所示。路基湿度现场调研工作开展情况如图3所示。

表1 路基湿度现场调研结果汇总
注:(1) 气候区划参照《公路自然区划标准》(JTJ 003—86)划定; (2)ntmi,即综合湿度指数,为表征气候因素的参量。

图3路基湿度调研现场工作图
2.2 大气降水入渗机理
降雨入渗会随着时空变动而产生动态变化[9],入渗量受降雨强度与历时、土体物性、渗入面坡度、植物覆盖状况等因素影响。当降雨强度大于土体入渗能力时,将在地表产生径流,进而向土体内部渗透,此时,土中水分运动模型可称为“积水模型”;而当降雨强度小于入渗能力时,入渗过程由供水能力控制,此时,土中水分运动模型可称为“降水模型”。
因此,大气降水入渗过程可分为两个阶段[10]:初始阶段地表入渗率较高,含水率梯度也较大,水分可无压或自由入渗,随着入渗过程持续不断,入渗率不断降低,含水率梯度也持续减小,当小于降雨强度时,水分开始有压入渗。因此,土体入渗量取决于土的初始含水率、降雨强度及持时、地表径流量等[11]。
降雨与地表积水入渗趋于稳定后,土体沿深度方向的含水率分布如图4所示,根据含水率分布情况,该剖面可划分为以下几个区域[9]:
(1) 饱和区:该区域处于饱和状态,其深度通常仅有几毫米。
(2) 过渡区:该区域的含水率随深度增加,迅速降低,通常也只有几厘米。
(3) 传导区:该区域的含水率随深度增加,变化较小,称其为稳定含水率,传导区通常为厚度较大的非饱和区域。
(4) 湿润区:该区域的含水率随深度增加,从稳定含水率下降到初始含水率附近。
(5) 湿润锋:干旱地区由于地下水位很深,在一定深度范围内,土体水源仅来自上部入渗水分,湿润锋即是在湿润区以下湿土和干土之间形成的陡水力梯度锋面。
由于路基上覆路面结构的阻水与防水效应,路基中的饱和区与过渡区含水率同传导区之间的差别并不显著,特别是在干旱地区,路基土体顶部水分积聚效应并不明显,在新疆乌奎高速公路K43+800处的现场调研也证实了这点(如图5所示),因此,本文将以上两区纳入传导区考虑,三区范围内路基土体湿度以稳定含水率表征,也即路基顶面以下80 cm深度范围内的工作区,其平衡含水率可用稳定含水率反映。

图4 土体含水率沿深度方向的典型分布图
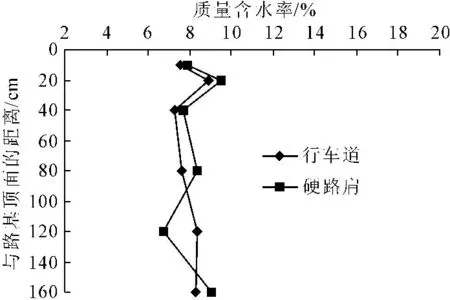
图5乌奎高速公路路基现场含水率竖向剖面图
3 路基湿度预估模型
3.1 模型建立
Perera Y Y[12]对美国多个地区40余条公路进行了调研,并收集了公路所在区域的气候资料,分析了路基基质吸力与年均相对湿度、降雨天数、地下水位、综合湿度指数ntmi、土性参数等的相关性。结果表明,不同土组的基质吸力与ntmi相关性最好,本文调研数据也证实了基质吸力与ntmi关联性较好,数据离散程度在一定范围之内(如图6所示)。因此,针对不同土组,以ntmi表征区域气候条件对路基平衡湿度状态下基质吸力的影响,建立如式(5)所示的指数函数形式的基质吸力预估模型。
hs=α{e[β/(ntmi+101)+γ]+δ}
(5)
ntmi指标包含了降雨、蒸发、温度、土组、太阳辐射等因素的影响,其中既包含了气候因素的影响,又包含了地理位置的影响,从而能全面量化一个地区干旱或者潮湿的程度(计算方法可参见文献[13]),因此,Perera Y Y所提出的基质吸力预估模型具有较高的通用性和精确性。
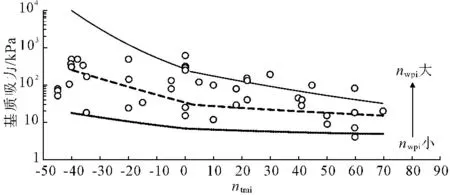
图6基质吸力与ntmi的关系图
从图6可以看出,基质吸力随ntmi的变化趋势与土组有关,本文采用加权塑性指数nwpi(nwpi=P200×IP,IP为塑性指数(%),P200为以十进制表示的通过200目(0.075 mm筛)的土粒含量,即细粒含量;)表征土组性质,相较单一的P200,反映的土组特性更为全面。
式(5)的α、β、γ、δ为模型的回归系数,ntmi后加上常数101是为保证分母“ntmi+101”不为0(文献[12]中路基湿度调研点的ntmi值均大于-100)。式(5)经过变形整理,得:
hs=αeγe[β/(ntmi+101)]+αδ
(6)
以α′、β′、γ′代替式(6)中的αeγ、β、αδ,可得:
hs=α′e[β′/(ntmi+101)]+γ′
(7)
上式指数部分分母中的常数不妨取整为100,以a1、a2、a3取代α′、β′、γ′,因此,式(7)可最终转变为:
hs=a1e[a2/(ntmi+100)]+a3
(8)
式中,a1、a2、a3为模型的回归系数,其值与土的物理性质即IP、P200或nwpi有关;nwpi为加权塑性指数,其值等于IP与P200之积。
式(8)与式(5)相比,参数减少了一个,使模型形式得到简化。
本文针对Perera Y Y提出的ntmi模型和ntmi简化模型,分别进行了回归分析,回归结果如表2所示,由表2可知两个模型回归效果相当(从模型回归所得相关系数来看)。如前所述,由于ntmi简化模型参数更少,形式更为简洁,考虑到模型应用的便利性,因此,本文采用ntmi简化模型(如式(8)所示)预估路基土的基质吸力。(无论是文献[12]的调研结果,还是本文现场调研结果,其ntmi值均大于-100,因此,式(8)中指数部分的分母“ntmi+100”恒大于0)。

表2 不同形式的ntmi模型回归结果比较
注:表中nwpi值为不同土组的上下限值。
表2中给出了不同土组的nwpi限值,其中,砂的IP和nwpi设定为0,其它三种土组IP、P200和nwpi的界限值如表3所示。
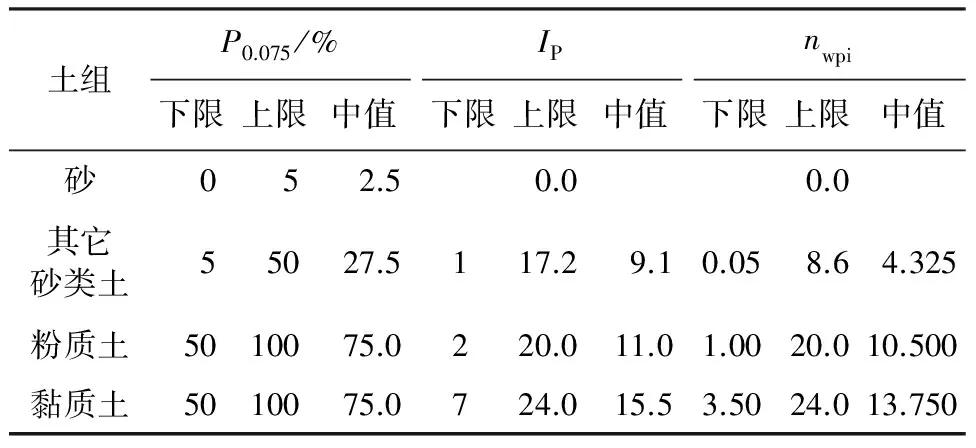
表3 不同土组塑性指标界限值
表3中不同土组的P200限值按其定义确定。其它砂类土的IP上、下限值确定为1.0与17.2[4],粉质土和黏质土的IP参照《公路土工试验规程》[14](JTG E40—2007),采用塑性图划分方法确定,另因《公路路基设计规范》[15](JTG D30—2004)中规定“液限大于50%、塑性指数大于26的细粒土,不得直接作为路堤填料”,所以,由此可以得到粉质土和黏质土的IP上、下限值,如表3所示。
文献[4]对我国多条已建成高速公路进行了湿度调研,所获数据如表4所示,结合文献[12]的调研数据,采用如式(8)所示的ntmi简化模型,进行数据拟合,回归结果如表5所示。
另外,通过F检验,得到7条曲线的F值均大于临界F值F0.05(显著性水平α=0.05),即F>F0.05。其中,3条曲线(nwpi=0.05、1.00、8.60)的F>F0.01(显著性水平α=0.01),说明回归模型非常显著,也即ntmi(因素)对hs(试验结果)具有非常显著的影响;4条曲线(nwpi=0.00、3.50、20.00、24.00)的F>F0.05,说明回归模型显著,也即ntmi(因素)对hs(试验结果)具有显著的影响。

表4 路基湿度现场调研数据[4]

表5 ntmi简化模型回归结果
综上所述,采用简化后的ntmi模型(如式(8)所示)具有统计学意义,表征ntmi与hs的关系是可行的。
式(8)所示的ntmi简化模型参数取值如表6所示。

表6 ntmi简化模型回归参数
3.2 模型验证
为验证ntmi简化模型的正确性与精确性,本文在我国西部的新疆、重庆、四川等较为干旱的地区选取不同等级公路的路基进行了基质吸力现场测试。
(1) 基质吸力现场测量。基质吸力是表征路基平衡湿度的理想指标,由于张力计使用方法简便,受调研现场环境干扰小,故本文采用张力计对服役路基的基质吸力进行了测量。为保证试验精度,在钻孔取样后,即刻把张力计放入钻孔中,并将钻孔取样剩余的原土回填、压实,保证测试土样与取得土样的一致性,基质吸力现场测量情况如图7所示。

图7基质吸力现场测试
现场测量基质吸力的大致步骤为:① 首先将无气水注满张力计,在水中浸泡陶瓷头5 min左右,而后用真空抽气机把真空表中气泡抽出,反复进行上述操作,直至完全抽出气泡; ② 其次合上张力计的密封盖(张力计已加满水并抽完气泡),在水中静置30 min左右,记下此时张力计的初始读数h0; ③ 然后开始测量基质吸力,一般来讲,测量直至张力计读数不变,或者在30 min内读数变化不超过1 kPa为止,这个过程通常持续4 h以上,具体时间与土质类型有关; ④ 张力计最终读数hs减去初始读数h0的差值即为所测土体的基质吸力。
(2) 模型误差分析。为使用ntmi简化模型预估路基土的基质吸力,本文在调研点采集土样(如图8所示),进行基本物性参数室内试验,获得ntmi简化模型所需参数。

图8路基湿度现场调研点所采集土样
现场实测值与ntmi简化模型预估值对比结果,如表7所示,两者之间的最大误差在30 kPa左右,绝对误差在2%~50%之间。

表7 基质吸力实测值与预估值(ntmi简化模型)对比
注:(1) 绝对误差=|hs,预估-hs,实测|/hs,实测; (2) 代数误差=(hs,预估-hs,实测)/hs,实测。
此外,本文还对现场实测值与地下水位模型(hs,预估=yγw,y为计算点与地下水位之间的竖向距离,γw为水的重度)[12]预估值进行了对比,两个模型对比结果的比较示意图如图9所示。
由图9可知,高基质吸力状况下,实测值与预估值之间的误差有所增大,这与张力计量程范围受限有关。张力计的量程大致为0~150 kPa,在土体较干或基质吸力较高时,由于发生“气蚀”现象而使量测系统进气,导致读数失真,测量精度下降,相应地,实测值与预估值之间的误差也有所增大。
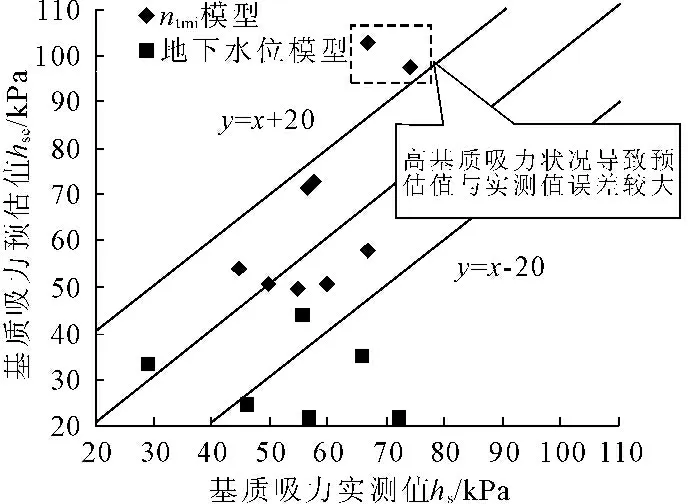
图9路基土的基质吸力预估值与实测值对比
为进一步分析基质吸力预估模型(ntmi简化模型和地下水位模型)的精度,采用式(9)分别对两种模型进行了误差统计分析,其结果如表8所示,表中剔除了图9中误差较大的两个点。
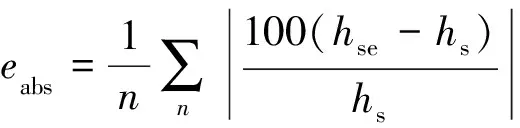
(9)
式中:eabs为绝对误差平均值,%;ealg为代数误差平均值(取绝对值),%;hs为基质吸力的实测值,kPa;hse为基质吸力的预估值,kPa;n为实测数据个数。

表8 基质吸力预估模型误差分析
误差分析的结果表明,在干旱、半干旱地区,ntmi简化模型误差远小于地下水位模型,上述地区路基湿度(在此,以基质吸力指标表征)受气候因素与土质类型的影响比地下水位埋深(以及波动程度)的影响更为显著。
4 结 语
(1) 基质吸力因沿路基深度方向的分布是趋于稳定和连续的,且与非饱和路基土的物理力学参数有着较好的相关性,所以被本文选为平衡湿度表征指标。
(2) 通过大气降水入渗机理分析,结合现场调研数据,本文明确路基土含水率在深度方向的分布规律,并以稳定含水率反映干旱地区路基工作区(路基顶面以下80 cm深度范围)土体湿度。
(3) 本文引入表征多种气候因素影响的综合湿度指数ntmi,构建适合干旱地区路基平衡湿度预估的气候效应模型即ntmi简化模型,采用新疆等地12个路段的路基湿度现场调研数据,对模型进行了验证,结果表明,预估值与实测值之间的绝对误差平均值为14.86%,代数误差平均值为3.36%,误差满足工程精度要求。
[1] Quintus H V, Killingsworth B. Analyses relating to pavement material characterizations and their effects on pavement performance[R]. Washington D. C.: Federal Highway Administration, 1998.
[2] Russam K, Coleman J D. The Effect of climatic factors on subgrade moisture conditions[J]. Geotechnique, 1961,11(1):22-28.
[3] Aitchison G D, Richards B G. A broad scale study of moisture conditions in pavement subgrades throughout Australia-the selection of design values for soil suction equilibria and soil suction changes in pavement subgrades (a symposium in print)[C]//Moisture Equilibria and Moisture Changes in Soils Beneath Covered Areas. Australia: Australia Butterworths, 1965:226-232.
[4] 曹长伟.路基湿度状况及模量调整系数研究[D].上海:同济大学,2007.
[5] Uzan J. Characterization of clayey subgrade materials for mechanistic design of flexible pavements[J]. Transportation Research Record, 1998(1629):188-196.
[6] Fredlund D G, H Rahardjo. Soil Mechanics for Unsaturated Soils[M]. New York: John Wiley & Sons Inc, 1993.
[7] D.G弗雷德隆德(加拿大),H·拉哈尔佐(印度尼西亚).非饱和土土力学[M].北京:中国建筑工业出版社,1997.
[8] Richards B G. Behavior of Unsaturated Soils (Soil Mechanics NEW Horizons, L K Lee ed. Chap.4)[M]. New York: Elsevier, 1994.
[9] 雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988.
[10] 谭 新,陈善雄,杨 明.降雨条件下土坡饱和-非饱和渗流分析[J].岩土力学,2013,24(3):381-383.
[11] 刘小平.非饱和土路基水作用机理及其迁移特性研究[D].长沙:湖南大学,2008.
[12] Perera Y Y. Moisture equilibria beneath paved areas[D]. Arizona: Arizona State University, 2003.
[13] 李 聪,凌建明,官盛飞.基于路基湿度预估的综合湿度指数[J].同济大学学报:自然科学版,2012,40(11):1672-1676.
[14] 交通部公路科学研究院.公路土工试验规程:JTG E40—2007[S].北京:人民交通出版社,2007.
[15] 中交第二公路勘察设计研究院.公路路基设计规范:JTG D30—2015[S].北京:人民交通出版社,2015.
ClimateDependencyofUnsaturatedSubgradeSoilsMoistureinAridRegions
LI Cong1,2, HUANG Ke3, WANG Zheng3
(1.ChinaMerchantsChongqingCommunicationsResearch&DesignInstituteCo.,Ltd.,Chongqing400067,China; 2.NationalEngineering&ResearchCenterforHighwaysinMountainArea,Chongqing400067,China;3.SchoolofCivilEngineering,ChongqingJiaotongUniversity,Chongqing400074,China)
In order to explore the relationship between the humidity of unsaturated subsoil and climate in arid regions, a series of tests have been done in this paper. Along with field investigation of subgrade moisture in typical areas of arid regions, we derived the distribution law for moisture of subgrade soils in depth direction. Then Thornthwaite Moisture Index (TMI) has been taken as representation of climate factors with matric suction selected to express subgrade moisture and climatic effect model has been established to reveal relationship between TMI and matric suction according to soils type. Finally, the acceptance of climatic effect model is verified by the data of field investigation. The results show that climatic effect model is more precise than groundwater table model in quantitative expression of influence of environment factors on subgrade moisture for aridity regions.
climaticeffectmodel;moistureequilibriaofsubgrade;matricsuction;Thornthwaitemoistureindex(TMI)
10.3969/j.issn.1672-1144.2017.06.004
2017-07-15
2017-08-20
国家科技支撑计划课题资助项目(2015BAK09B01);国家自然科学基金资助项目(51508496);重庆市青年科技人才培养计划资助项目(cstc2014kjrc-qnrc30004)
李 聪(1980—),男,四川宣汉人,高级工程师,工学博士,主要从事路基工程、道路地质灾害评估与防治等方面的研究。E-mail: licong@cmhk.com
U416.0
A
1672—1144(2017)06—0016—07

