悬挂工装对运载火箭模态试验影响分析

汤 波，范瑞祥，潘忠文，张永亮

(1. 北京宇航系统工程研究所，北京100076；2. 中国运载火箭技术研究院，北京100076；3. 北京强度环境研究所，北京100076)

悬挂工装对运载火箭模态试验影响分析

汤 波1，范瑞祥2，潘忠文1，张永亮3

(1. 北京宇航系统工程研究所，北京100076；2. 中国运载火箭技术研究院，北京100076；3. 北京强度环境研究所，北京100076)

为分析悬挂工装对运载火箭模态影响，通过系统能量泛函建立了悬挂梁系统的振动方程和边界条件，得到了系统固有频率特征方程，并证明自由-自由边界模型是其蜕化情况。通过数值求解特征方程，得到了系统频率和振型相对于悬挂工装的长度、密度变化的规律。采用此方法解释了某型火箭模态试验出现的多组一阶横向模态现象。

火箭；模态；自由-自由边界；悬挂工装；悬挂梁

0 引 言

火箭模态特性是姿控稳定性设计和Pogo抑制分析的基础。美国德尔塔-3运载火箭由于设计时未考虑一组关键滚转模态，首飞中滚转失控，最终火箭自毁。我国首次载人航天飞行中，宇航员经受较大的低频振动，原因是推进系统和结构纵向耦合振动相互耦合产生的自激振动。因此研究火箭的全箭动特性十分重要。

目前国内外航天器动特性建模和修正方法的研究已经成熟。Leadbetter[1]开展了土星V号运载火箭动特性建模，王建民等[2]总结了捆绑火箭的模态分布特点，给出了捆绑火箭横、纵、扭模态互相耦合的特征，潘忠文等[3]系统研究了蒙皮加筋结构的拉压、弯曲和扭转刚度以及桁条面积等效、惯性矩等效对此类结构刚度特性的影响，邱吉宝等[4]针对仿真模型与试验结果的一致性，总结了模型修正的方法，Pan[5]从圆柱壳体、推进剂和局部振型斜率预示三个方面对建模方法进行了综述。

航天器空间状态与地面试验状态存在差异，Hsu等[6]研究了重力对航天器动力学响应影响，马睿等[7]研究了重力影响下太阳翼模型修正方法。我国目前采用柔性悬挂方法模拟火箭飞行时的自由边界，但其天地一致性尚未发现相关的文献结果。一般认为，当悬挂系统的固有频率小于试验件一阶固有频率的1/5时，其对结构弹性模态频率的影响可以忽略[8]，在试验结束以后的模态分析中，也不会考虑悬挂系统对模态参数识别结果的影响。在我国新一代中型运载火箭模态试验时，发现由于悬挂系统影响，系统出现了多组一阶横向振动频率。本文通过将试验系统抽象为悬挂梁模型，推导了固有频率特征方程，得到了系统频率和振型相对于悬挂工装的长度、密度变化的规律，理论分析结果与有限元计算及试验结果吻合。揭示了火箭规模变大后，悬挂工装对全箭模态试验影响越来越大，大幅增加了试验和结果分析的复杂度，有必要采用油气支撑装置代替目前的悬挂工装开展模态试验[9]。

1 理论与数值分析

1.1 悬挂梁振动方程

当前我国运载火箭模态试验时采用弹性绳将火箭悬吊在空中模拟自由-自由边界条件。为分析系统振动规律，将火箭建模为欧拉梁，将悬挂绳建模为张力为常量的弦，两者组成悬挂梁系统如图1所示。

梁、弦的最大动能与势能分别为

(1)

(2)

式中:ω为系统的固有频率，ρ为梁或弦的线密度，u为位移，E为材料的弹性模量，I为截面惯性积，F为弦内张力，在小变形假设下等于梁的重量；L表示梁或弦的长度，下标1,2分别代表梁和弦。

系统固有频率满足泛函[10]

(3)

其中,u2在悬挂点满足强制边界条件，即u2(L2)=0，且梁与弦连接点位移相同，即u1(0)=u2(0)。分部积分后得到

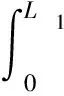
(4)

因u1,u2的变分是任意的，从积分项可得悬挂梁振动方程为

(5)

(6)

式(5)和式(6)表明悬挂梁系统不改变振动方程，只改变边界条件。式(5)的通解为

(7)

式中：C1,C2,C3,C4,D1,D2为6个待定系数，由边界条件求得，另外有

(8)

1.2 方程的蜕化情况

式(5)和式(6)存在如下两种蜕化情况：

1) 当F=0时，蜕化为不带工装的梁模型。

2) 当ρ2=0时，蜕化为单摆+梁模型。

F=0时，对应γ=0，此时边界条件(6)的第4式变为u‴1(0)=0，与前3式构成两端自由梁的边界，系统蜕化为不带工装的梁模型。

ρ2→0时，η→0，此时式(7)变为u2=ηD1β2x+D2，其中ηD1为有限值，此式代表了单摆的振动方程。

1.3 悬挂梁固有频率方程

将式(6)代入式(5)，可得边界条件方程为

(9)

再补充振型归一化方程，此处不妨设C2=1，从式(9)求得

(10)

从而

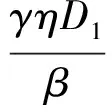
(11)

从式(9)可以得到

(12)

将式(12)代入式(11)得到

活猪调运受限的局面在未来较长的时间内难以改变，猪肉调运或将逐渐成为趋势。活猪调运是导致疫情扩散的主要原因之一，如果活猪长期受限，短期内由于产地和销地不匹配、屠宰和养殖产能的不匹配，猪价的区域性差异将会持续；长期看，养殖和屠宰产能的分布将更加合理。

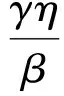
[sin(βL1)cosh(βL1)-cos(βL1)sinh(βL1)]=0

(13)

式(13)为悬挂梁固有频率的特征方程。特别地，当γ=0时，上式左边第3项为0，方程蜕化为两端自由梁的频率方程。

1.4 固有频率解的性质

式(13)为超越方程，只能求出其数值解。令

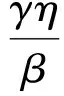
(14)

分析β变化时Y的过零区，可得到特征方程的解β，从而得到固有频率ω。

下述数值计算时假设E1I1=1,ρ1=1,L1=1，从而ω=β2,F=9.8。在示性分析中，可假设以上数值为无量纲化，因此数值中不写单位。

1.4.1不考虑悬挂系统(Free-Free Beam,FB模型)

Y=1-cos(βL1)cosh(βL1)

(15)

计算得到两端自由梁前四阶频率分别为22.37, 61.67, 120.9, 199.9 rad/s。

1.4.2单摆悬挂系统(Pendulum+Beam,PB模型)

当F≠0，ρ2=0时，式(14)可写为

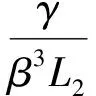
(16)

获得PB模型固有频率随单摆频率比变化规律如图2所示。其横坐标为单摆与FB模型的一阶固有频率之比，纵坐标为频率，黑色区域的边缘为系统的固有频率，从图2可得如下结论：

1) PB模型固有频率随工装长度降低而升高，工装越长越接近FB模型，无限长时等价于FB模型。

2) 悬挂工装长度为0时(单摆固有频率为无穷大)，PB模型等价于一端铰支、一端自由的梁。

3) 随着悬挂工装长度缩短，PB模型各阶次的固有频率单调递增，此阶次频率介于FB模型和一端铰支、一端自由的梁相应阶次固有频率之间。

4)当摆梁固有频率比为1/5时[8]，在本文初始参数下，原两端自由梁一阶基频上升6%。

1.4.3悬挂梁系统(Chord+Beam,CB模型)

当F≠0，ρ2=0.01和ρ2=0.1时获得CB模型固有频率随摆梁频率比变化规律如图3所示。

由图3可知悬挂工装的线密度固定时：

1) 悬挂工装长度较短时，CB模型固有频率与PB模型接近，可不考虑悬挂工装的弦振动特性。

2) 悬挂工装长度较长时，CB模型出现了较为丰富的频率成分。在原PB模型的模态附近，出现多组模态。悬挂工装自身大量模态与梁耦合，在试验中，将造成频率识别的困难，以及采集振型的偏离。

3) 同样的悬挂工装长度，悬挂工装线密度升高，CB模型更容易出现多个频率成分。

4) 悬挂工装长度极长时，β值的微小变化均会导致ctan(β2ηL2)的快速变号，而式(14)的其它值基本不变，因此在β的微小邻域内存在大量的固有频率解，此时模态试验已无法开展。

当γ≠0，L2=0.5和L2=2时获得CB模型固有频率随摆梁频率比变化规律如图4所示。由图4可知悬挂的长度固定时：

1) 随着悬挂工装线密度增加，CB模型同阶次固有频率单调下降，且下降速率呈先快后慢趋势。

2) 随着悬挂工装线密度增加，在原PB模型一阶弹性频率附近，出现多个固有频率成分。

3) 悬挂工装长度增加后,随着其线密度增加,CB模型同阶次固有频率下降速率增大，低频附近固有频率成分增加。

1.5 振型性质

悬挂工装线密度增加，系统频率降低，振型改变不明显；悬挂工装长度增加，振型一致程度增加。而且悬挂工装长度增加，系统中出现新的振型。图5显示了ρ2=0.10,L2=1.00时频率ω=33.64 rad/s的新振型(FB模型的一、二阶频率分别为22.37 rad/s和61.67 rad/s)，此振型与FB模型的振型具有一定的相似性，但两者频率差异较大，将给试验结果分析带来较大困扰。

2 试验分析

由第1.1节和1.2节可知，当悬挂工装长度较长时，系统中将出现新的振型，且振型与FB模型的振型具有一定的相似性，其试验结果将给模型修正带来一定的困难。

我国新一代中型运载火箭模态试验时，火箭通过悬挂系统模拟自由-自由边界条件。悬挂系统由井字梁、作动筒、蝶形弹簧、调节拉杆、钢丝绳和承力框组成，悬挂系统如图6(a)所示。

在某秒点时，全箭重量约为220 t，全箭总长约50 m，悬吊工装长度为26 m，分为4组，每组4根钢丝绳组成，每根钢丝绳半径约为25 mm。不考虑悬挂工装时，计算可得出一组一阶横向模态(将Y、Z向的一对视为一组)，频率都为1.73 Hz。

由于火箭构型复杂，无法精确换算出其相关等效参数。但对于一阶频率，仍可将之视为简单梁模型，换算线密度ρ1约为4400 kg/m，根据梁自由-自由状态频率特征方程的解，得出E1I1约为6.5×109kg·m3，γ约为3.3×10-4m-2·s-2，η约为13 m·s。计算得出此工况下Y值与不考虑工装情况下的对比如图7所示。由图7可知，考虑工装后，频率由原一组变成了三组。绘制悬挂工装为不同长度或不同根数对全箭一阶频率的影响如图8所示。由图8可知，当悬挂工装长度为26 m 或每组悬挂工装为4根时，正好出现较为接近的三组频率成分。

为准确分析工装对全箭频率和振型的影响，建立火箭有限元模型如图6(b)所示。不考虑工装时，计算中出现一组一阶模态，将此组模态与试验中出现的两组模态同时进行比较,如图9所示。

计算模型中加入工装后，计算频率对比见表1，振型对比见图10和图11。由于此处悬挂工装为4组，出现了多于三组的模态。试验中采集到的两组一阶横向频率成分在计算中均可以找到，且计算频率与试验结果更为接近。

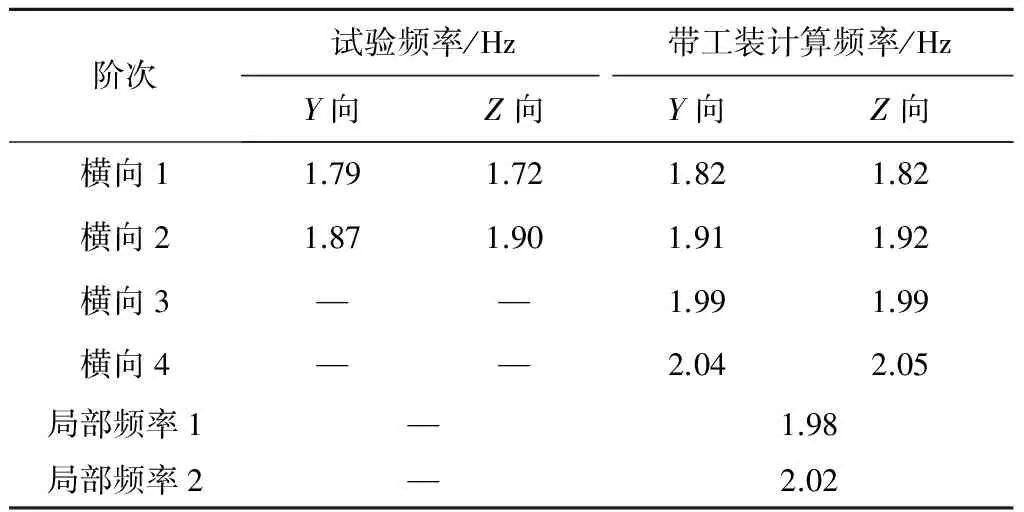
表1 带悬挂工装计算与试验频率对比表Table 1 Comparison of frequency between computation with suspension rope and experiment

3 结 论

本文将悬吊工装视为弦，抽象运载火箭模态试验模型为悬挂梁(CB模型)，建立固有频率特征方程，并开展数值求解，得到了系统频率和振型相对于悬挂工装的长度、密度变化的规律，解释了我国新一代中型运载火箭模态试验时出现的多组一阶横向模态现象，理论分析结果与有限元计算及试验结果吻合。

[1] Leadbetter S A. Application of analysis and models to structural dynamic problems related to the Apollo-saturn V launch vehicle[R]. NASA TN D-5831, 1970.

[2] 王建民, 荣克林, 冯颖川, 等. 捆绑火箭全箭动力学特性研究[J]. 宇航学报, 2009, 30(3):821-826. [Wang Jian-min, Rong Ke-lin, Feng Ying-chuan, et al. The research of dynamic characteristics for the strap-on launch vehicle[J]. Journal of Astronautics, 2009, 30(3):821-826.]

[3] 潘忠文, 王小军, 马兴瑞, 等. 基于梁模型的蒙皮加筋结构纵横扭一体化建模研究[J]. 中国科学(E辑:技术科学)，2014, 44(5): 517-524. [Pan Zhong-wen, Wang Xiao-jun, Ma Xing-rui, et al. Longtidinal-lateral-torsional integrated modeling based on a beam model for skin-stiffened structure[J]. Sci.Sin.Tech., 2014, 44(5):517-524]

[4] 邱吉宝, 王建民. 运载火箭模态试验仿真技术研究新进展[J]. 宇航学报, 2007, 28(3):515-521. [Qiu Ji-bao, Wang Jian-min. The recent progresses on research into modal test simulation techniques for launch vehicles[J]. Journal of Astronautics, 2007, 28(3): 515-521.]

[5] Pan Z. Reviews in structural dynamics analogy technique of launch vehicle [J]. Advances in Mechanics, 2012, 42(4):406-415.

[6] Hsu S T, Griffin J H, Bielak J. How gravity and joint scaling affect dynamics response[J]. AIAA Journal, 1989, 27(9): 1280-1287.

[7] 马睿, 姜东, 吴邵庆, 等. 考虑重力影响的太阳翼模型修正方法研究[J]. 宇航学报, 2014, 35(12):1373-1378 .[Ma Rui, Jiang Dong, Wu Shao-qing, et al. A model updating method for solar array considering the influence of gravity [J]. Journal of Astronautics, 2014, 35(12):1373-1378.]

[8] GJB 2706A—2008, 航天器模态试验方法[S].

[9] Tuma M L, Chenevert D J. Ensuring safe exploration: ares launch vehicle integrated vehicle ground vibration testing[C]. AIAA Space Ops Conference, Huntsville, USA,Apr 25-30, 2010.

[10] 倪振华. 振动力学[M]，西安：西安交通大学出版社，1989:390.

EffectsofSuspensionRopeonModalExperimentofRockets

TANG Bo1, FAN Rui-xiang2, PAN Zhong-wen1, ZHANG Yong-liang3

(1. Beijing Institute of Astronautical System Engineering, Beijing 100076, China;2. China Academy of Launch Vehicle Technology, Beijing 100076, China;3. Beijing Institute of Structure & Environment, Beijing 100076, China)

The vibration equations and boundary conditions are established from the energy function of a beam system which is suspended with ropes; subsequently, the natural frequency characteristics equation is acquired. It is demonstrated that the free-free boundary model is the degenerated condition of the beam system. By solving this characteristics equation numerically, the natural frequency and modal relative to the length or density of the suspension rope is obtained. The appearance of the multiple first-order modals in a certain rocket’s modal test is explained by using this method.

Rocket; Modal; Free-free boundary; Suspension rope; Suspended beam

2017- 02- 20;

2017- 09- 22

V416

A

1000-1328(2017)12- 1354- 07

10.3873/j.issn.1000- 1328.2017.12.013

汤波(1982-)，男，博士，主要从事运载火箭载荷和动特性方面的研究。

通信地址：北京市9200信箱10分箱18号(100076)

电话：(010)68755946

E-mail:tangbot@sina.com