基于传递函数和小波变换的变压器故障诊断研究
陈子龙 冀卓婷 郑 重 董芃欣
(1. 西安交通大学电气工程学院,西安 710049;2. 重庆大学电气工程学院,重庆 400044)
基于传递函数和小波变换的变压器故障诊断研究
陈子龙1冀卓婷2郑 重2董芃欣2
(1. 西安交通大学电气工程学院,西安 710049;2. 重庆大学电气工程学院,重庆 400044)
电力变压器的安全运行对电力系统的正常工作至关重要,如何及时有效地诊断变压器故障是保障电网安全运行的重要问题。本文针对变压器绕组变形后的传递函数进行了分析,并采用小波变换的方法对频响曲线的能量谱进行了探究,寻找了故障的严重程度和位置与频响曲线能量间可能的关系。研究表明故障严重程度和频响曲线高频成分的能量呈负相关,但故障位置和高频成分能量间无明显关联。
传递函数;小波变换;能量谱;扫频法
变压器作为保障电力系统正常运行的关键设备,一旦发生故障,就会严重威胁电力系统的安全运行。并且,电力变压器价格昂贵,如果发生故障后不能及时维修,一旦损坏会造成较大的经济损失。国内外变压器故障统计资料表明[1-2],变压器故障多为出口短路故障,在短路电流引发的安培力作用下,绕组极易发生扭曲变形,如何及时有效地发现变压器的故障是一个重要且困难的问题。自从E. P. Dick和C. C. Erven提出谐波阻抗法诊断绕组变形以后,已经出现了相当多的绕组变形诊断方法。如:短路阻抗法、低压脉冲法、频率响应法(FRA)和振动频响法等,这些方法有的已经较为完善,例如:频率响应法已经被实际应用在工程问题中并有了相关标准。虽然频响法已经有了很大的发展,但现在对频响曲线仍然缺乏合理的解释。已有的方法大都通过对故障前后频响曲线的变化对故障进行推测,例如:有些文献[3-5]通过对频响曲线的极值点的变化判断绕组有无变形,还有一些文献[6-11]通过对比故障前后频响曲线的相关系数来判断绕组是否发生变形,虽然这些方法能在一定程度上判别绕组有无故障,但难以对故障进行量化分析,也没有找到频响曲线和故障间的联系,为此,本文从传递函数的角度对频响曲线进行了分析,并探究了故障和频响曲线可能的关联。
传递函数可以看作是电路结构的数学体现,能有效的反应电路的重要特征,并且,频域的传递函数恰好为电路的幅频响应,所以,通过分析电路的传递函数来对电路状态进行评价是一种有效的方法。现有方法对传递函数的应用大都为利用拟合算法得到的传递函数的零极点来判断有无故障发生,对频响曲线和传递函数间的联系没有进行详细研究。另外,现有方法在对频响曲线的分析时大多采用简单的信号处理方法进行特征提取,难以挖掘频响曲线的深层次信息,虽然也有应用小波变换的方法对故障进行检测[12-18],但这一信号处理方法主要应用在振动法里,振动法通过测量变压器油箱壁的振动信号对变压器状态进行检测,可以实现在线监测,但该方法容易被负载电流、电压、温度等因素影响[19-23],对振动信号的特征提取亦是一个困难的问题,所以振动法的效果仍然不够理想。另外,振动信号仅是变压器运行状态某一方面的信息,传递函数则是变压器内部结构的等效体现,相对来说,传递函数包含的变压器运行状态方面的信息更加丰富。因此,在综合考虑传递函数和小波变换的特点后,本文分析了故障前后变压器等效电路传递函数的变化,然后利用小波变换优异的信号处理能力,探究了频响曲线和故障间的联系。
1 分析处理方法
1.1 实验原理
电力变压器在超过 1kHz电压的作用下,可以等效为由电容、电感和电阻组成的无源线性二端口分布参数网络,如图1所示,考虑到电阻对电位分布影响较小,所以等效电路模型可以看成由电容、电感组成,如图2所示。

图1 绕组简化等效模型
如果把等效电路划分成许多个模块,并且令每一模块均由纵向电容、电感和对地电容组成,那么等效电路可以看成由许多小模块电路级联组成,如图2所示。
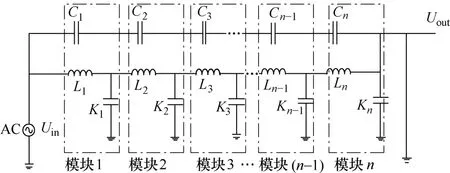
图2 绕组模块化等效模型
假设在无故障时每一个模块电路的传递函数为N( s),等效电路由n个模块电路组成,那么,由模块电路表示的变压器的传递函数可以表示为

假设绕组某一部分发生变形,变形的绕组对应的模块电路的传递函数由()N s变为()N s˜,发生变形的模块总数为n˜,那么,故障后的传递函数可以表示为
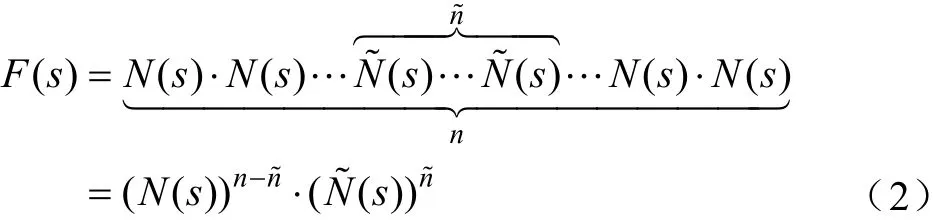
对上述传递函数取对数,可以得到:
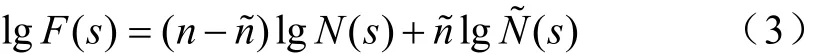
式中,n为总的模块数;n˜为发生变形的模块数;N( s)为正常模块对应的传递函数;N˜( s)为变形模块对应的传递函数。 N ( s)是一个确定的代数式,但是N˜( s)的代数形式却是难以确定的,因为绕组变形的方式非常复杂,在电动力的作用下,绕组有可能向内弯曲,亦有可能向外弯曲,扭曲后的绕组形状也很不规则,不同的故障下N˜( s)的形式都有所不同,所以,N˜( s)的代数形式很难写出。为此,参考数学变量分析的观点,我们把N˜( s)看作一个变量,且该变量相对 N ( s)小得多(一般发生变形的绕组数较少),另外,考虑到变形绕组的不规则形状和正常绕组的区别,N˜( s)所含的s的阶数可能和N( s)是不同的。
在上述分析的基础上,把传递函数转化到频域,可以得到

式中,lg F ( jw)恰好为频响曲线,(n -n˜) l g N (jw)为正常模块对应的信号,该信号是确定的且占比较大;n˜ l g N ˜ ( jw)为变形模块对应的信号,该信号是不确定的且占比较小, n˜ l g N ˜ ( jw)在不同的故障下是不一样的,但是应该和(n -n˜ ) l g N (jw)所包含的s阶数不一样。综上,频响曲线可以看成两个频率变化速度不一样的信号组成的。反过来看,如果能从频响曲线里分离出这两个信号,通过对故障模块对应的信号进行分析或许可以得到绕组变形的有用信息。
因为(n -n˜ ) l g N (jw)和 n˜ l g N ˜ ( jw)包含的s的阶数不一样,所以这两个信号随着频率的变化快慢也不一样,如果信号里包含的s的阶数越多,那么该信号对频率变化的响应就会越快。如果能把频响曲线里不同频率成分的信号区分出来,或许就可以分辨出(n -n˜) l g N (jw)和 n˜ l g N ˜ ( jw)。所以,本文利用小波变换优异的分频能力对频响曲线进行分析,以寻找频响曲线不同频率成分和故障的联系。
1.2 小波变换原理
小波变换的多分辨理论为人们讨论信号的局部信息提供了一个相当直观的框架。这一点在非平稳信号里尤为重要,因为非平稳信号的频率随时间而变化,这种变化可以分为慢变和快变的两部分。慢变部分对应非平稳信号的低频部分,代表信号的主要轮廓;快变部分对应信号的高频部分,代表信号的细节信息。
1)信号分解
如果φ和ψ分别为尺度和小波函数,那么信号f在分辨率 2j-1下的近似和细节部分 Dj-1f分别假设为
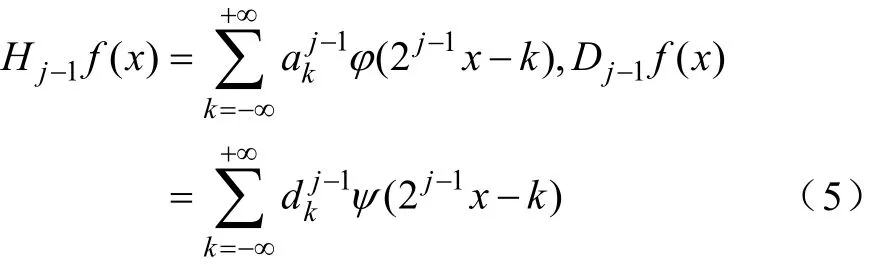

若f∈Vj,则Hjf=f,并且式(6)等价表示为
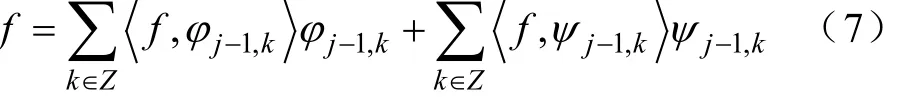
为了令空间jV的信息分解到子空间1jV-和1jW-里,分别由{ f ,φj-1,k}确定空间 Vj-1,{ f ,ψj-1,k}确定空间 Wj-1,因此对(8)实施相应的内积运算,并利用双尺度方程产生信号的分解公式可以得到分解信号。

2)信号重构
利用上述的信号分解公式和基函数{φj,k}的正交性,令 f ={φj,k},可以得到

在式(8)里令 f ={φj,k},并且利用式(9)可以得到重构方程:

值得注意的是,上式为双尺度分解方程的逆形式。为了得到分解后的信息,利用{ f,φj-1,l}和{ f,ψj-1,k}重构空间 Vj的相关信息,对(10)作内积可以得到如下的重构公式
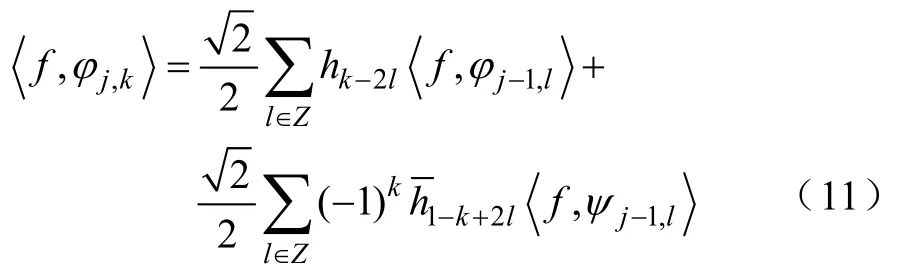
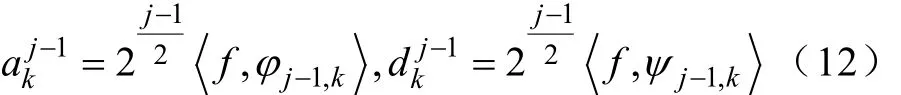
(1)信号分解公式
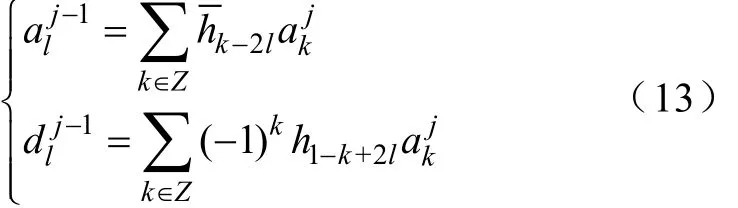
(2)信号重构公式

最后,可以得到尺度函数φ生成的正交多分辨的主要步骤,归纳如下:
①由空间基函数Vj确定尺度函数;
②构造小波空间;
③确定小波包;
④寻找小波变换正交基;
⑤对信号进行分解;
⑥对分解后的信号重构并进行能量谱变换。
2 实验分析
试验仪器为一台 SY-30/10型三相双绕组变压器,变比为10∶9,每相绕组有60个线饼,绕组内每间隔一个饼引出一个饼内抽头,共29个抽头。
实验时,将绕组线圈按纵向均匀分为14等份,并从不同等分点引出抽头,在抽头上分别设计不同类型的故障。当探究故障严重程度和频响曲线能量间的关系时,在同一抽头和地间分别串联 47pF、100pF、220pF的电容;当探究故障位置和频响曲线能量间的关系时,分别在绕组的 4等分点、8等分点和10等分点抽头和地间串联47pF电容,在实验过程中尽量保证只有一个变量变化。
实验流程为先由信号发生器输出正弦电压信号,输出信号经放大器放大后输入试验变压器,然后通过信号采集卡收集变压器响应信号,最后输出响应信号到工控机中。输入正弦信号幅值为 20V,频率范围为0~1000kHz,实验仪器图如图3所示。

图3 实验仪器
2.1 故障严重程度和高频信号能量的关系
本文先进行扫频法试验,得到频响曲线后,利用Matlab编程对频响曲线进行小波变换,然后求变换后信号的能量谱,最后,分析在不同的故障状况下的信号能量谱的特点。
得到的变压器无故障时的频响曲线如图4所示。对信号进行小波变换后,得到的4层dB1型小波分解信号如图 5所示,为研究信号的低频部分特点,分解信号前4节点得到的信号如图6所示,最后,可以得到不同频率区间信号的能量谱如图 7所示,应注意的是,图 7显示的是不同频率区间的信号能量所占总信号能量的百分比,而非信号的绝对能量。
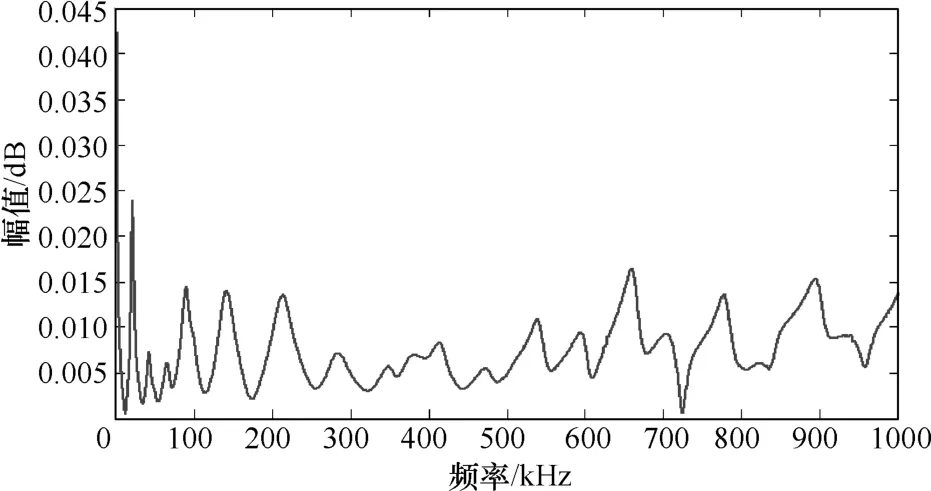
图4 无故障时的频响曲线

图5 无故障时的4层次分解信号
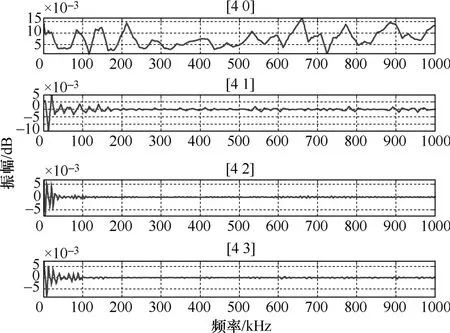
图6 无故障时的前4个频率区间的信号
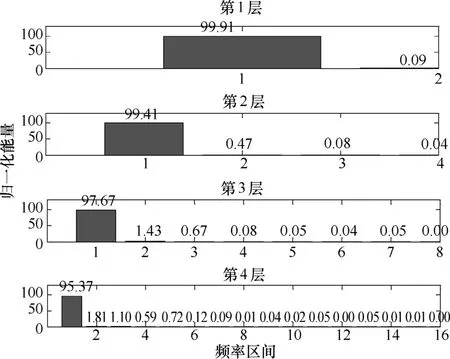
图7 无故障时的能量谱
图7 中的信号是对频响曲线变换后得到的能量谱信号,因为进行了 4层小波变换,所以图中有 4层信号,在每一层信号区间中,按序号由高到低对频率的由高到低,以第4层信号为例,“1”区间的频率最低,“16”区间的频率最高。从图7可以发现,随着分解层次的增加,高频信号的能量占比更容易分辨,以图7的第2层信号为例,因为第1频率区间信号能量和过大,得到的第2频率区间信号能量和占总信号能量的比重仅为 0.47,但若分解的层次增加,则高频信号所占的比重就能更明显的被分辨出来,同样以图7来看,第4层信号的第2频率区间信号能量和占总信号能量的比重为 1.81,所以,多层次小波分解能把复杂的信号分解为更细致的频率区间,从而能更加有效地分辨信号里微弱的高频成分,以便找到高频成分对应的故障信息,所以,多层次小波变换是有效的。
为了寻找故障严重程度和高频成分能量的联系,分别在变压器绕组的4等分点和地间串联47pF、100pF和200pF的电容,并对得到的频响曲线进行小波变换,得到的频响曲线能量谱如图8所示。

图8 串联47pF电容时的能量谱

图9 串联100pF电容时的能量谱

图10 串联200pF电容时的能量谱
从图7至图10可以发现,相对变压器无故障时的能量谱,高频成分的能量有较为明显的降低,低频信号的能量有较为明显的增加,例如第四层信号第一频率区间(对应低频成分)的能量在无故障时为95.37,串联47pF电容后变为99.77,串联100pF电容后变为99.79,串联200pF电容后变为99.79。
在图8至图10还可以发现,当串联的电容增大,也就是对应的绕组变形加重时,前4个频率区间的低频成分的能量占比逐渐增加,例如第2层信号的第1频率区间的能量和分别由99.97变为99.98,再变为99.99,虽然能量变化的幅度较小,但相对无故障时的信号来看低频信号的能量仍然有所增加。这说明,随着故障程度增加,故障点的杂散电容增加,对应的低频信号的能量增加,故障严重程度和频响曲线低频成分的能量成正相关,而和高频成分呈现负相关的特点。
另外,还可以从频响曲线小波变换的前4个频率区间(对应低频成分)来观察故障严重程度和高频成分能量的关系,如图11至图13所示,从[4 2],[4 3]能明显地发现,当串联电容值增加时,信号的振幅明显增加,信号波动加剧,说明低频信号能量增加,高频信号能量降低,这同样说明故障严重程度和频响曲线高频成分的能量成负相关。

图11 串联47pF电容时前4个频率区间的信号
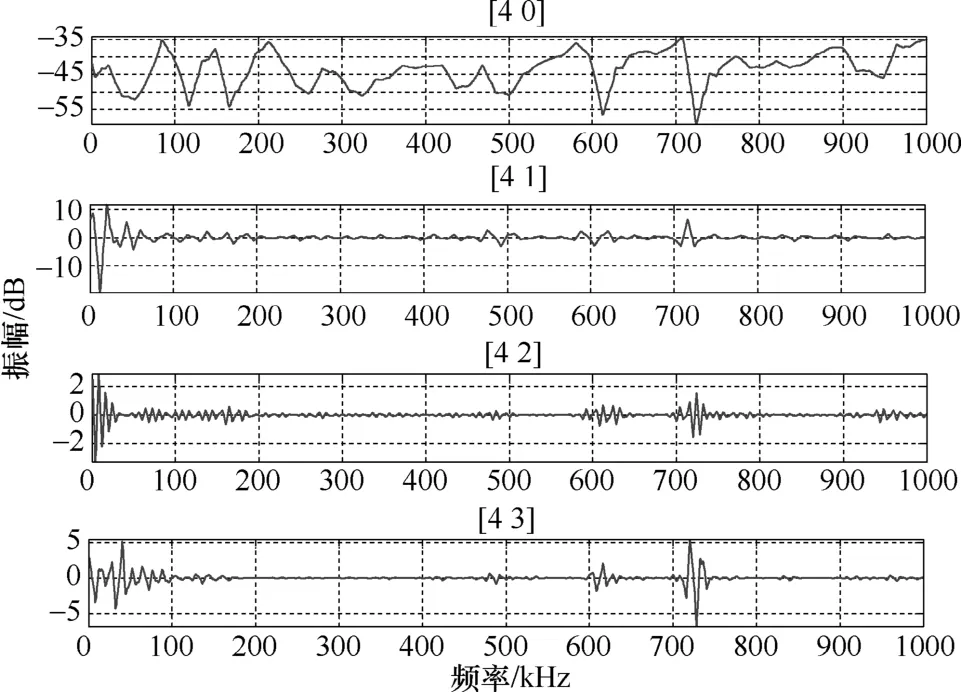
图12 串联100pF电容时前4个频率区间的信号
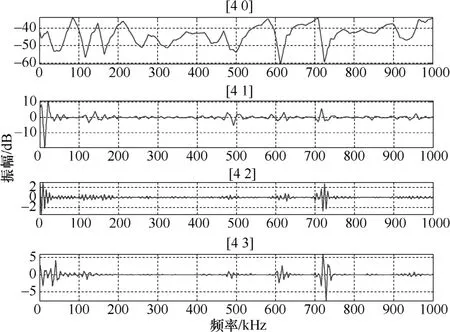
图13 串联200pF电容时前4个频率区间的信号
2.2 故障位置和高频信号能量的关系
为了分析故障点和高频成分能量的对应关系,设定故障点的位置分别为变压器绕组的4等分点、8等分点和10等分点,并在对应的故障点和地间分别串联47pF的电容,然后进行扫频法实验,并对得到的扫频信号进行小波变换。得到的不同故障的能量谱如图14至图16所示,从图中可以发现,当故障位置发生变化时,小波变换后得到的高频信号的能量谱近似不变,这说明,高频信号的能量变化和故障位置无明显关联,所以不能用该方法辨别故障位置。

图14 在4等分点串联电容时的能量谱

图15 在8等分点串联电容时的能量谱

图16 在10等分点串联电容时的能量谱
从图14至图16还可以发现,当改变故障点的方位,保持故障程度不变时,前4个频率区间的能量占比近似不变,高频信号的能量占比也近似不变。这主要是因为虽然故障点位置改变,但从能量和的角度来看,因为故障的严重程度不变,所以对变压器的结构改变的贡献程度近似不变,所以能量分布无明显变化。说明该方法难以分辨故障点方位。
另外,还可以从频响曲线的小波变换前四个频率区间的信号来观察绕组变形严重程度和高频信号能量的关系,如图17至图19所示,当串联电容位置改变时,前4个频率区间信号的波形振幅几乎相同,信号波动程度相近,这说明信号高频成分的能量分布不变。
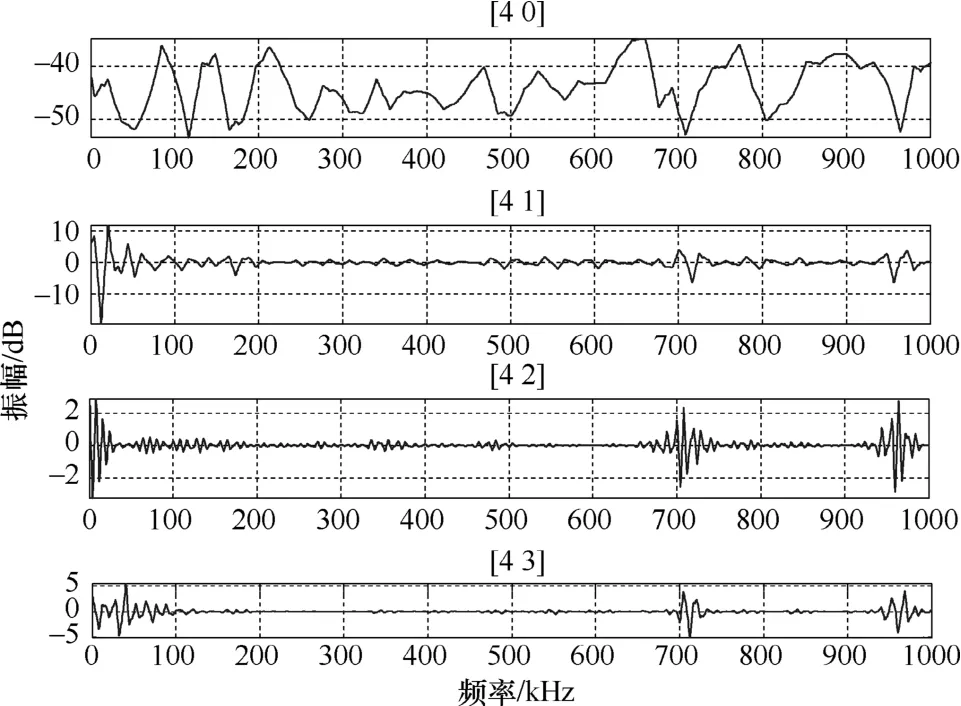
图17 在4等分点串联电容时前4个频率区间的信号

图18 在8等分点串联电容时前4个频率区间的信号
3 结论
本文通过小波变换的方法对模拟电压器故障时的扫频信号进行了能量谱分析,研究表明:
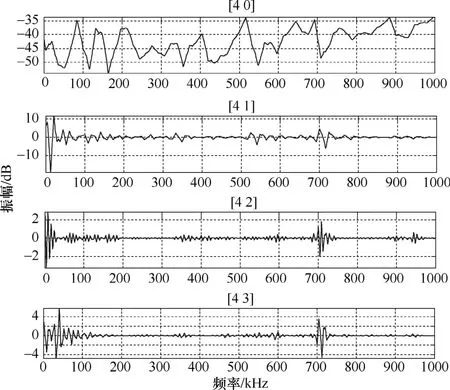
图19 在10等分点串联电容前4个频率区间的信号
1)扫频信号的高频成分的能量和故障严重程度呈现较为明显的负相关性,当变压器故障状态加重时,扫频信号高频成分的能量会有所降低,所以可以用扫频信号高频成分的能量来量化的反映故障的严重程度。造成这一现象的主要原因可能是变形绕组的传递函数发生变化,令扫频信号的不同频率成分的占比发生变化,但是变形绕组的传递函数的详细变化状况还有待进一步研究。
2)本文在研究时还发现,变压器故障点的位置和扫频信号高频成分的能量间没有明显的联系,难以用该方法定位变压器的故障点。
[1] 胡忠平, 廖福旺, 兰生. 变压器绕组辐向稳定性研究[J]. 电气技术, 2017, 18(4): 32-38.
[2] 李林锐, 郑浩, 刘厚康, 等. 变压器振动监测系统检测装置的设计与实现[J]. 电气技术, 2015, 16(12):6-9, 51.
[3] 刘效真, 高占岭, 李秀国, 等. 一起变压器绕组变形故障的分析与判断[J]. 电气技术, 2015, 16(8): 92-94.
[4] 张秀斌, 吕景顺, 温定筠, 等. 基于频率响应法的110kV主变压器绕组变形案例分析[J]. 电气技术,2015, 16(4): 97-100.
[5] 齐宇婷, 杨学昌, 周文俊. 基于传递函数的电力变压器绝缘故障加信诊断方法[J]. 电力系统自动化,2002, 26(1): 27-31.
[6] 武剑利, 舒乃秋, 彭凌烟. 变压器绕组传递函数的拟合原理及绕组变形诊断应用[J]. 电力自动化设备,2004, 24(6): 88-90.
[7] 闫贻鹏, 邱丛明, 朱伟剑. 基于正交多项式的变压器传递函数的辨识方法[C]//2013年中国电机工程学会年会论文集, 成都, 2013.
[8] 陈凌. 电流源法检测变压器绕组变形[D]. 成都: 西华大学, 2008.
[9] 高勇. 油浸变压器类设备绕组的分数阶模型研究[D].北京: 华北电力大学, 2016.
[10] 武剑利. 频响分析法检测变压器绕组变形的理论研究[D]. 武汉: 武汉大学, 2004.
[11] 张喜乐, 梁贵书, 董华英, 等. 变压器绕组的特快速暂态建模[J]. 电工技术学报, 2007, 22(3): 55-59, 78.
[12] 王丰华, 李清, 金之俭. 振动法在线监测突发短路时变压器绕组状态[J]. 控制工程, 2011, 18(4):596-599.
[13] 陈梁远, 黎大健, 赵坚, 等. 基于振动模型的变压器绕组变形特性研究[J]. 广西电力, 2016, 39(4):22-25.
[14] 盛连军, 金胤豪, 曹斌, 等. 变压器振动法在线监测技术[J]. 上海电力学院学报, 2014, 30(5): 451-455.
[15] 马宏忠, 耿志慧, 陈楷, 等. 基于振动的电力变压器绕组变形故障诊断新方法[J]. 电力系统自动化,2013, 37(8): 89-95.
[16] 朱光伟, 张彼德. 电力变压器振动监测研究现状与发展方向[J]. 变压器, 2009, 46(2): 23-24.
[17] 郭洁, 黄海, 唐昕, 等. 500kV 电力变压器偏磁振动分析[J]. 电网技术, 2012, 36(3): 70-75.
[18] 张彬, 徐建源, 陈江波, 等. 基于电力变压器振动信息的绕组形变诊断方法[J]. 高电压技术, 2015, 41(7):2341-2349.
[19] 吕妍, 王伟, 李智. 电力变压器绕组变形常用检测方法[J]. 山东电力技术, 2013(5): 46-49, 52.
[20] Aballe A, Bethencourt M, Botana F J, et al. Wavelets transform-based analysis for electrochemicalnoise[Z].1999: 266.
[21] Aballe A, Bethencourt M, Botana F J, et al. Using wavelets transform in the analysis of electro chemical noise data[Z]. 1999: 4805.
[22] Mitola J. The software Radio architecture[J]. IEEE Communication Magazine, 1995, 33(5): 26-38.
[23] Ostachowicz W, Kudela P, Malinowski P A. Damage localisation in plate-like structures based on PZT sensors[J]. Mechanical Systems and Signal Processing,2009, 23(6): 1805-1829.
Transformer Diagnosis based on Wavelet Transform and Transfer Function
Chen Zilong1Ji Zhuoting2Zheng Zhong2Dong Pengxin2
(1. Department of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049;2. Department of Electrical Engineering, Chongqing University, Chongqing 400044)
The safe operation of power transformers plays an important role in the safety of electrical power system. How to effectively diagnose the transformer fault is an important problem to ensure the safe operation of the transformer. In this paper, the increase of stray capacitance and fault resistance leads to the increase of transformer operation noise, as a result, The energy spectrum signal of the sweep signal of the transformer is analyzed by wavelet transform to explore the relationship between the fault severity, fault location and the energy of the high frequency signal. The study shows that the severity of the transformer fault is positively related to the energy of the high frequency component of the sweep signal, but there is no obvious correlation between the fault location of the transformer and the energy of the high frequency component.
transfer function; wavelet transform; energy spectrum; frequency sweeping method
陈子龙(1993-),男,硕士研究生,主要从事绕组变形检测和局部放定位方面的研究工作。

