遗传算法优化Prony电力系统谐波检测的研究

葛江红 张昌丽

（1. 国网滁州供电公司，安徽 滁州 239000；2. 国网芜湖供电公司，安徽 芜湖 241000）

遗传算法优化Prony电力系统谐波检测的研究

葛江红1张昌丽2

（1. 国网滁州供电公司，安徽 滁州 239000；2. 国网芜湖供电公司，安徽 芜湖 241000）

实现对电力系统所含谐波的快速、准确检测是对其进行有效抑制、以提高电能质量和增强电网稳定性的关键技术。本文通过对现有电力系统谐波检测方法的比较，通过分析含噪声条件下传统Prony算法的相关参数优化选择方面存在的局限性，并根据Prony算法可以直接提取待检测信号的相关参数的特征，同时具有较强的自适应能力等特点，提出了遗传算法优化 Prony电力系统谐波检测方法，以实现对 Prony方法检测谐波相关参数的优化求取。通过仿真实验表明，本文所提出的方法对于不同信噪比条件下的谐波检测信号在拟合误差精确度以及稳定性等方面均具有显著的优势。

谐波检测；遗传算法；Prony算法

随着电力电子技术的快速应用以及非线性负荷需求的不断增加，由此所导致的电力系统谐波对电能质量造成了严重的影响。近年来，谐波等相关原因所造成的大面积停电事故时有发生，这不仅对人民群众的正常生产生活带来了极大的不便，而且对国民经济的发展造成了巨大的损失。在此背景下，为了减小甚至避免电力系统谐波对于电网正常运行的不利影响，准确而有效地对电力系统谐波进行检测并适时采取相应的抑制措施，已成为电力系统安全稳定运行的一项决定性要素[1-2]。

目前对于电力系统谐波检测方面的方法主要有：模拟滤波器谐波检测方法、希尔伯特-黄变换检测方法、基于神经网络的检测方法、基于傅里叶变换的检测方法、基于小波变换的检测方法、基于Prony算法的谐波检测方法等[3]。其中模拟滤波器检测方法硬件电路设计简单，易于实现，然而其中心频率带有参数敏感性，在实际中难以获得满意的特性参数，从而使得检测结果存在较大的误差。希尔伯特-黄变换检测方法对于非线性非平稳信号具有较强的适用性，具有计算量小的优势，然而其在谐波检测过程中易出现模态混叠等问题，导致对于多成分信号分解稳定性较差。基于神经网络的检测方法对于训练样本具有较高的依赖性，同时缺乏标准化的神经网络模型构造方法与流程[4]。基于傅里叶变换的检测方法计算量较大，计算效率不高，此外当待检测信号的频率与采样频率不相匹配时，易产生频谱泄露效应（栅栏效应），从而造成较大的检测误差。作为一种信号时域分析中所广泛采用的工具，应用小波变换检测并分析电力系统谐波信号具有较强的普遍性，其可对待检测信号中的奇异值进行准确定位进而判断其相应的干扰类型。然而在实际检测过程中，如何选择合适的小波基函数对信号进行分离目前尚无统一化的指导原则，此外小波变换无法准确检测谐波信号的频率与对应的幅值[5]。这些因素都限制了上述方法的广泛应用。

扩展 Prony算法模型可以直接提取待检测信号的幅值、频率、初相以及衰减因子，具有较强的自适应能力，无需对特征方程进行求解，也不必进行样本自相关的估计验算，仅借助于对多项式与线性方程组的求解便可得到精确度高的模态信号[6-7]。然而，模型参数的选择制约着 Prony算法信号检测的最终结果，在含噪声条件下这一问题将变得越发突出。基于此，本文提出利用扩展的Prony 算法进行电力系统谐波检测过程，以启发式的智能优化算法-遗传算法对 Prony的相关参数（包括幅值、相位、频率以及衰减因子）进行在线优化选择，克服离线模型参数选择对谐波检测结果的不利影响，从而最终实现提升 Prony算法谐波检测精度，减少系统误差的目的。本文对含有不同噪声强度的谐波信号进行了基于Matlab平台的仿真实验研究，结果显示该方法相比于传统的 Prony算法准确度有了显著的提升。

1 扩展Prony算法理论分析

1795年由法国数学家Gaspard Riche和Baron de Prony联合提出了Prony算法。该方法最初应用于气体膨胀问题的研究，其基本机理为通过一系列的指数函数的线性组合对待测信号进行拟合，以获取待测信号的幅值、相位、频率以及衰减因子，其数学表达式定义如下：

式中，Ai为幅值；αi为衰减因子；iφ为相角；fi为余弦信号的频率，P为阻尼余弦分量的个数。

对于离散时间谐波检测信号 x(n)=[x(0), x(1), …, x(N-1)]，0≤n≤N-1，利用 Prony 方法对上述信号进行拟合的数学表达式为

式中，采样间隔为Δt。

假设式（2）中有衰减直流分量 p1个，衰减余弦分量p2个，利用欧拉公式将对应的余弦分量展开表示，同时令p=p1+p2，则离散时间表示的待检测谐波信号的函数形式为

式中，k为模型的阶数；N为采样点的个数，且N≥2n，ˆ()x n为x(n)的拟合估计值；bi和zi为对应的复数。为了实现信号估计值与待检测信号值的精确匹配，利用平方误差最小的原则，求得上式中的相关参数解，使得估计值与真实值之间的平方误差最小。Prony算法认为式（2）中的信号拟合过程是一个常系数线性差分方程的齐次解。为此定义多项式：

对式（2）两边同时乘以ak，再对p+1个乘积求和，整理得

定义 e(n)为真实待检测信号 x(n)与其估计值ˆ()x n之间的误差，则有

根据上式有

扩展 Prony算法即是求解上述方程的线性最小二乘解。根据式（7）中的参数 a1, a2,…, ap可求得特征方程式1+a1z-1+…+apz-p=0的根，即为Prony的极点。根据zk的取值，式（2）即可化简为线性方程，其相应的矩阵形式表示如下：

由上述推导过程可知，扩展 Prony算法的实质是将非线性求解问题转换为线性差分问题进行求解，通过最小二乘法实现曲线拟合过程，以对信号中的各个参数值进行计算。

2 遗传算法优化Prony的谐波检测

2.1 遗传算法原理

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法[8-9]。遗传算法是从代表问题可能潜在解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体（individual）组成。每个个体实际上是染色体（chromosome）带有特征的实体。在初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

2.2 遗传算法优化Prony谐波检测流程

利用遗传算法优化扩展 Prony方法以实现对电力系统谐波检测的目的，通过遗传算法的寻优过程可得出谐波参数（幅值Ai、相位iφ、频率fi以及衰减因子αi）的最优取值。相应的具体流程如下。

1）初始化。设置最大进化代数T，随机生成M个个体作为初始群体 P(0)，其中每个个体的维度为各个幅值Ai、相位iφ、频率fi以及衰减因子αi的个数之和，此外设置交叉规模 pn、交叉概率 pc与变异概率pm。

2）个体评价。计算基因群体P(t)中各个个体的适应度值，其中t表示当前进化代数。

3）选择运算。将适应度高的个体直接遗传到下一代或是通过配对交叉以产生新的个体再遗传到下一代，本文选择俄罗斯轮盘赌的概率生成方式实现个体的选择过程。

图1 遗传算法优化Prony谐波检测流程图

4）交叉运算。基于预先设定的交叉概率 pc对任意两个个体进行交叉操作以产生新的个体p*。

5）变异运算。按照变异概率对群体中的某些个体上的某些基因位置上的染色体值进行随机变动。

6）群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。

7）终止条件判断。若t=T，则为进化过程中所得到的具有最大适应度值的个体，并将其作为最优解输出，终止计算过程。

基于本文所提出的遗传算法优化 Prony谐波检测方法，可以实现对输入待检测谐波信号的非线性拟合，同时以在线优化参数机制克服了传统谐波分析方法对谐波频率无法精确估计的不足，有效提升谐波幅值以及相角的计算精度与稳定性。

2.3 遗传算法优化Prony谐波检测参数求解步骤

1）基于上式构建样本函数 r(i,j)，并以此为基础计算扩展阶数的方程矩阵形式，即

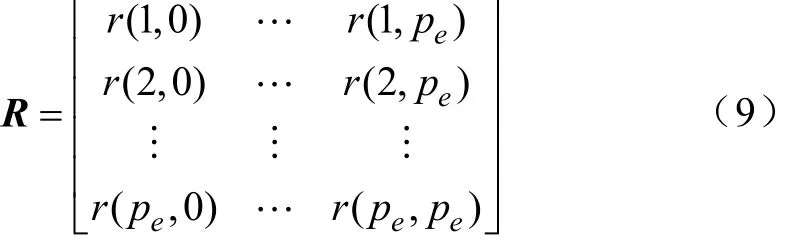
2）通过最小二乘估计确定矩阵 R的有效秩 p以及参数a1, a2,…, ap。

3）对多项式 1 + a z-1+ . ..+ a z-p= 0 计算其特征

p根 zk，1≤k≤p，令 xˆ( n ) = x(0)，计算参数 b1, …, bp。4）利用谐波频率建立遗传算法优化目标函数，即

通过遗传算法寻优过程得出最优解（Ai, Bi），i=1, 2, …, p，以此为基础，算得谐波的幅值与相角。

电力谐波信号中往往含有随机噪声信号，基于传统 Prony谐波检测方法所得到的各次谐波的幅值与相角存在比较大的误差，这也是传统 Prony算法对实际谐波信号分析的局限性所在。利用遗传算法的在线启发式参数寻优的优势，以及在曲线拟合方面的稳定性强、精度高的优点，构建基于在线遗传算法Prony参数寻优的改进Prony谐波检测方法通过对输入信号进行非线性的拟合，计算出相应的幅值与相角，同时对于频率的估计精度有望改善和提升。

3 仿真实验

为了验证所提出的遗传算法优化 Prony电力谐波检测方法的有效性，本文采用相关电力谐波检测文献中广泛采用的算例，其中相应的谐波模型信号为

其中测试信号中含有基波、3次以及5次谐波，此外还含有40Hz和125Hz频率的间谐波信号。取采样频率为1000Hz，其中采样点数为50个，同时分别在 y(t)信号中叠加 50dB、40dB的白噪声。在Matlab平台上，分别对传统的Prony谐波检测方法以及本文所提出的遗传算法优化 Prony谐波检测方法对测试信号进行拟合，比较两种方法的相关性能。对应的拟合误差结果如图2和图3所示。

图3中，Prony谐波检测方法在50dB信噪比条件下的平均误差为 0.1310，在 40dB信噪比条件下的平均误差为0.1523；而遗传算法优化Prony谐波检测方法在上述不同信噪比下的平均误差分别为0.0628与 0.0616。上述结果表明，信噪比变小对Prony谐波检测方法具有不利影响，其拟合误差有增大的趋势，从而说明该方法对于信号中的噪声较为敏感。而遗传算法优化 Prony谐波检测方法拟合误差平均值有显著的下降，计算结果精度显著改善（约为Prony方法的50%左右）；同时，该方法随着信噪比的下降平均拟合误差变动不大，说明该方法对于引入的噪声具有较好的抑制以及消除作用。此外，Prony检测方法的拟合误差在时间轴上分布不均，且有较大的分布区间，在50dB和40dB信噪比条件下的最大误差值分别达到了0.4018和0.4326。

图2 50dB信噪比下谐波检测拟合误差图

图3 40dB信噪比下谐波检测拟合误差图

从图4可知，本文所提出的遗传算法优化Prony谐波检测方法在幅值估计值以及相角估计值的拟合误差方面较传统的 Prony谐波检测方法具有显著的优势。在信噪比为50dB时，遗传算法优化Prony谐波检测方法基波分量幅值的绝对值误差为 0.0236，而传统的Prony谐波检测方法的绝对误差为0.0713，所提出的遗传算法优化 Prony谐波检测的误差精度下降了约66.7%；同时所提出的遗传算法优化Prony谐波检测方法的相角误差也明显减少。

4 结论

本文以扩展 Prony谐波检测方法为基础，针对其存在的噪声条件下在线参数（包括幅值、相位、频率以及衰减因子）匹配选择问题，以启发式遗传算法对Prony谐波检测相关参数进行优化选取，设计了相关了方法流程以及参数计算步骤。进行与传统 Prony谐波检测方法的仿真实验比较，结果显示本文所提出的方法在拟合误差精度、稳定性等方面具有显著的优势。

图4 50dB信噪比下幅值与相角估计误差

[1] 熊杰锋, 李群, 袁晓冬, 等. 电力系统谐波和间谐波检测方法综述[J]. 电力系统自动化, 2013, 37(11)：125-133.

[2] Asiminciaei L, Blaabjerg F, Hansen S. Detection is key-Harmonic detection methods for active power filter applications[J]. IEEE Industry Applications Magazine, 2007, 13(4)： 22-33.

[3] 杨洪耕, 惠锦, 侯鹏. 电力系统谐波和间谐波检测方法综述[J]. 电力系统及其自动化学报, 2010, 22(2)：65-69.

[4] 谷文静, 金涛. 基于小波变换的电力系统谐波分析研究[J]. 电气技术, 2012, 13(8)： 36-40.

[5] 何巨龙, 王根平, 刘丹, 等. 配电系统谐波扰动的定位与识别研究[J]. 电气技术, 2016, 17(12)： 25-30.

[6] 郭成, 李群湛, 贺建闽, 等. 电网谐波与间谐波检测的分段Prony算法[J]. 电网技术, 2010, 34(3)： 21-25.

[7] 陈晓芳, 赵成勇. 基于特定频带的Prony暂态振荡检测方法[J]. 电测与仪表, 2011(5)： 1-5.

[8] 王超学, 田利波. 一种改进的多目标合作型协同进化遗传算法[J]. 计算机工程与应用, 2016, 52(2)： 12-18.

[9] 叶满园, 周琪琦, 蔡鸿, 等. 基于多种群遗传算法的多电平逆变器多波段 SHEWM技术[J]. 电工技术学报, 2015, 30(16)： 111-119.

Power System Harmonic Detection based on Prony Optimized by Genetic Algorithm

Ge Jianghong1Zhang Changli2
(1. State Grid Chuzhou Power Supply Company, Chuzhou, Anhui 239000;2. State Grid Wuhu Power Supply Company, Wuhu, Anhui 241000)

The realization of fast and accurate detection of power system harmonics is the key factor to effectively suppress harmonics, to improve power quality and enhance the stability of power grid. Through the comparison of the existing power system harmonic detection method, by analyzing the limitation of parameter optimization selection of the traditional Prony algorithm under noise conditions,and according to the fact that Prony algorithm can directly extract the characteristic parameters of the detected signal, and having the characteristics of strong adaptive ability, this paper proposes the power system harmonic detection method based on Prony optimized by genetic algorithm, in order to achieve the optimization selection of related parameters. Simulation results show that the proposed method has significant advantages in fitting error, accuracy and stability for harmonic detection signals under different signal-to-noise ratio conditions.

harmonic detection; genetic algorithm; prony algorithm

葛江红（1972-），女，安徽滁州人，本科，工程师，研究方向为无功电压电能质量。