基于粒子群优化的KNN分类算法改进研究

吴敬学

（顺德职业技术学院 设计学院，广东 佛山 528333）

基于粒子群优化的KNN分类算法改进研究

吴敬学

（顺德职业技术学院 设计学院，广东 佛山 528333）

针对传统KNN算法寻找近邻耗时过多的不足，提出利用粒子群优化算法搜索近邻。粒子初始化为k个训练样本的编号，对于每一代：个体最优pbest定义为当前粒子与上一代pbest搜索到的最近邻集合，群体最优gbest定义为当前pbest搜索到的最近邻集合。并在迭代过程中建立距离表，通过距离表的更新与查询避免重复计算。对比实验表明，改进算法在分类精度不减甚至略微提高基础上，耗时缩短80%以上。

KNN；粒子群优化；文本分类

文本分类是可用于数字图书馆的一项重要技术。常用的分类方法有：决策树﹑最大熵﹑k近邻﹑遗传算法﹑神经网络﹑朴素贝叶斯﹑支持向量机﹑基于投票的方法﹑Rocchio分类等［1］。其中，k近邻（k nearest neighbor，KNN）算法作为向量空间模型（VSM）下最好的分类算法之一［2］，由Cover和Hart于1967年提出［3］，基本思想是：在VSM表示下，分别计算待分类样本与训练样本的距离或相似度，找出与待分类样本最相近的k个近邻，根据这k个近邻的类别确定待分类样本归属。KNN方法基于类比学习，是一种非参数的分类技术，在基于统计的模式识别中非常有效，对于未知和非正态分布可以取得较高的分类准确率，具有鲁棒性﹑概念清晰等诸多优点［4］。

但是，作为一种懒惰学习方法，KNN算法不具备离线训练阶段，所有计算都在分类过程中完成，同时，由于需要与训练样本逐个比较以确定待分类样本的近邻，计算开销大，分类效率低，这也限制了其在大数据﹑Web分类等方面的应用。为了提高KNN算法效率，目前常见方法有减小样本集规模和采用快速搜索算法。前者可通过特征降维和训练集剪裁实现。特征降维，如基于遗传算法的特征选择［5］﹑基于向量聚合技术的特征抽取［6］等，是文本分类的重要预处理过程，但降维后的向量通常仍具有高维性和稀疏性。训练集剪裁，如Editing方法［7］﹑Condensing方法［8］以及基于密度的剪裁［9］等，能有效降低计算开销，但已有研究成果表明，分类准确率和样本规模呈正相关性［10］，因此这种方法会损失一定精度。采用快速搜索算法，是另一种常用方法，又分为局部最优搜索与全局最优搜索。局部最优搜索是在训练集中选取或生成一些代表样本，通过与代表样本的比较，划定一个最有可能包含k个近邻的样本集合，并在此集合内进行精确搜索，如文献［11］利用Rocchio方法计算各类的原型向量，并通过比较得到k0个候选类别，然后在k0个类中心区域进行精确搜索，文献［12］则对每个类别内的相似样本聚类生成m个簇，通过文本串接得到各簇代表向量，并以此代替原始样本建立分类模型。局部最优搜索能够较大程度降低计算开销，但只是在局部范围内进行精确匹配，真正的近邻可能由于代表样本选取不当而错过，因此无法保证找到精确的k个近邻。全局最优搜索主要利用三角不等式原理，通过构建判别式，排除不可能成为近邻的训练样本，如文献［13］首先在训练样本中确定一个基准点R，然后根据基准点R﹑测试样本x和训练样本i三点之间几何关系构造不等式，判断是否将样本i排除，文献［14］则基于小波变换，利用向量的方差和在小波域中的逼近系数构造不等式，排除不可能成为近邻的样本。全局最优搜索需要对全部样本进行考察，将不可能成为近邻的样本排除，因此在降低计算开销方面较局部方法稍差，但其能够在全局范围找出精确的k个近邻，保证分类精度不变。本文利用粒子群优化算法搜索近邻，在全局范围内，根据个体最优和群体最优进行有指导地搜索，在保持或近似保持分类精度不变的情况下，提高分类速度。

1 粒子群优化算法

美国心理学家Kennedy和电气工程师Eberhart根据鸟类在觅食过程中通过自身经验与相互之间的信息共享能够迅速发现散落分布的食物这一现象，于1995年提出了粒子群优化（particle swarm optimization，PSO）算法［15］。算法的基本思想是：随机初始化一群没有体积没有质量的粒子，将每个粒子视为目标问题的一个可行解，粒子的好坏根据具体问题的适应度函数计算。粒子根据速度更新位置，而速度则通过个体最优和种群最优计算得到。

粒子群优化算法的数学表述为：假设在D维搜索空间中，粒子种群规模为N，则第i（i=1，2，...，N）个粒子的位置和速度分别表示为Xi=（xi1，xi2，...，xiD） 和 Vi=（vi1，vi2，...，viD）， 该 粒 子 所经历的最佳位置（pbest）表示为Pi=（pi1，pi2，...，piD），种群中所有粒子所发现的最佳位置（gbest）记为Pg。对于第t+1（t≥1）次迭代，粒子i在第d（d=1，2，...，D）维上的速度和位置分别依据式（1）和式（2）进行更新：

其中，w为惯性权重，其大小决定了粒子对当前速度继承的多少，选择一个合适的w有助于PSO均衡它的探索能力与开发能力。Shi等指出较大的惯性权重有利于展开全局寻优，而较小的惯性权重则有利于局部寻优，并提出从0.9线性递减到0.4的惯性权重策略［16］，采用这种惯性权重的PSO算法也称为标准PSO算法。c1和c2称为学习因子，也称加速常数，分别用于控制粒子指向自身或邻域最佳位置的运动，体现了粒子的自我认知和向群体最优学习的能力，通常取 c1=c2=2［17］。r1和r2为［0，1］范围内的均匀随机数。同时，粒子速度往往被限制在［-vmax，vmax］内，vmax增大，有利于全局搜索；vmax减小，则有利于局部开发［18］。但是，vmax过大可能使粒子步长过大从而飞过最优解导致难以收敛；vmax过小则可能使粒子步长太小导致陷入局部搜索空间而无法进行全局搜索［19］。vmax的值通常根据经验确定，并一般设定为问题空间的10%～20%［18］。

文献［20］认为，标准PSO中的“速度”概念并不是必需的，反而可能造成粒子“发散”，影响收敛速度与精度，并给出粒子进化过程与速度无关的证明，提出一种简化的粒子群优化算法sPSO，粒子位置更新由（3）式决定。

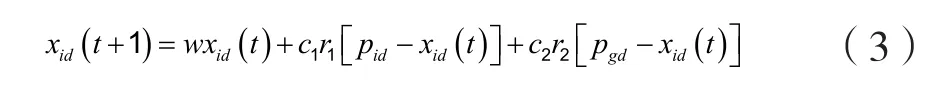
sPSO算法取消标准PSO中粒子速度的概念，避免了人为确定参数［-vmax，vmax］对粒子收敛速度和收敛精度的影响。

2 基于sPSO的改进KNN算法

KNN算法的一个重要步骤是搜索待分类样本的k个近邻，庞大计算开销也由此而来。设训练集为T，任意k个训练样本组成的集合为T*，不难证明，若T*是待分类样本x的最近邻组合，那么其中各样本到x的距离之和必然最小，则KNN算法搜索近邻的过程可视为在T中寻找T*的组合优化问题，约束条件为T*中各样本到x的距离之和最小。因此，可利用PSO算法搜索k个近邻。文献［21］基于标准PSO算法实现近邻搜索，但并未给出［-vmax，vmax］参数设置。本文采用文献［20］提出的简化粒子群算法sPSO，给出一种改进的KNN算法sPSO-KNN，该算法取消速度概念，避免人为确定参数［-vmax，vmax］对收敛速度和收敛精度的影响，在保持分类精度不降的条件下提高分类速度。

2.1 粒子编码

由于本问题的目标解为k个最近邻组成的集合，则粒子编码应为k个训练样本的编号。处理这类离散型问题，应对标准PSO算法加以修改。Kenney等曾在经典PSO基础上提出用于解决0-1整数规划的二进制版本的离散PSO（BPSO）算法［22］，另外也有学者通过取整函数直接将连续PSO用于任务分配问题［23］。通过实验得出，BPSO方法计算量较大，不适合本文应用，因此采用十进制数表示训练样本编号，并通过“向上取整”函数取整。另外，在进化过程中，若样本编号小于1则置为1，若大于训练样本数则置为训练样本数。

2.2 粒子评价与 pbest、gbest更新

通过实验得出，以距离之和最小作为评价粒子的标准，以粒子位置直接更新个体最优pbest和群体最优gbest的方法，其效果并不理想。因此，对粒子评价与pbest﹑gbest更新策略进行修改。对于每一次迭代：

1）不再对粒子进行评价，只是计算粒子中各训练样本到待分类样本距离。

2）pbest更新操作为：计算pbest及本代粒子中的各训练样本到待分类样本距离，对结果按升序排序，将距离最小的前k个样本的编号作为pbest。

3）gbest更新操作为：计算所有粒子pbest中的训练样本到待分类样本距离，对结果按升序排序，将距离最小的前k个样本的编号作为gbest。

同时，对于每一个待分类样本，在内存中建立所有训练样本到其的距离表，每次计算距离前先进行查询，若该训练样本已经过比较，则直接调取距离，若未经过比较，则计算距离并更新距离表，以此避免重复计算带来的多余开销。

2.3 算法步骤

基于sPSO算法搜索近邻的步骤如下：

步骤1 初始化。随机生成粒子，每个粒子为k个训练样本的编号，每个粒子的pbest即为其本身，gbest为所有粒子的训练样本中，与待分类样本距离最小的前k个样本的编号。

步骤2 更新粒子。按照式（3）对粒子状态进行更新。

步骤3 计算距离。对于各个粒子所代表的训练样本，查询距离表，若该样本尚未经过比较，则计算其到待分类样本之间距离，并更新距离表。

步骤4 更新pbest﹑gbest。依据2.2介绍的方法，从距离表中调取距离并对pbest﹑gbest进行更新。

步骤5 判断终止。若本代gbest中各训练样本到待分类样本距离之和与上一代相等，则终止迭代并输出最近邻组合gbest，否则转至步骤2。

3 对比实验

3.1 实验数据

实验数据采用中科院自动化所整理的中文新闻语料［24］，该语料集包含8个类别，其中训练样本数为13 025，测试样本数为3 254。本研究所选类别及各类包含的训练样本﹑测试样本数量如表1。

表1 实验语料类别及样本数量

3.2 实验设置

采用IG方法进行特征选择，设置两组实验，特征词数分别为500和1 000，对比算法为sPSO-KNN与传统KNN，每组实验分别设置测试样本数为200﹑500﹑2 166三轮。近邻数为15，粒子数为10，学习因子c1=c2=2，惯性权重w为0.9至0.4递减，相似性度量采用欧式距离，类别判断采取多数法。每种算法执行10次，取平均值作为最终实验结果。

3.3 结果与分析

改进算法sPSO-KNN与传统KNN算法对比实验结果的统计数据如表2。

从表2可以看出，改进算法sPSO-KNN在保持精度不降甚至稍微提高基础上，执行时间大大缩短。在不同实验条件下，改进算法耗时减少均在80%以上，说明改进算法在提高分类速度方面具有稳定性。另外，特征词数为500时，耗时减少平均为82.9%；特征词数为1 000时，耗时减少平均为85.49%，说明随着样本规模增大，改进算法速度的提高也越来越显著。

通过对实验数据的进一步分析发现，对于每个测试样本，利用sPSO方法搜索近邻的进化代数平均为10代左右，由于粒子数设置为10，近邻数为15，则理论上确定该测试样本的k个近邻需要经过约1 500次相似性比较，远低于传统KNN算法的8 669次。同时，通过对距离表的监测发现，实际上经过相似性比较的训练样本数平均为1 100个左右，说明设置距离表所避免的重复计算开销接近30%。

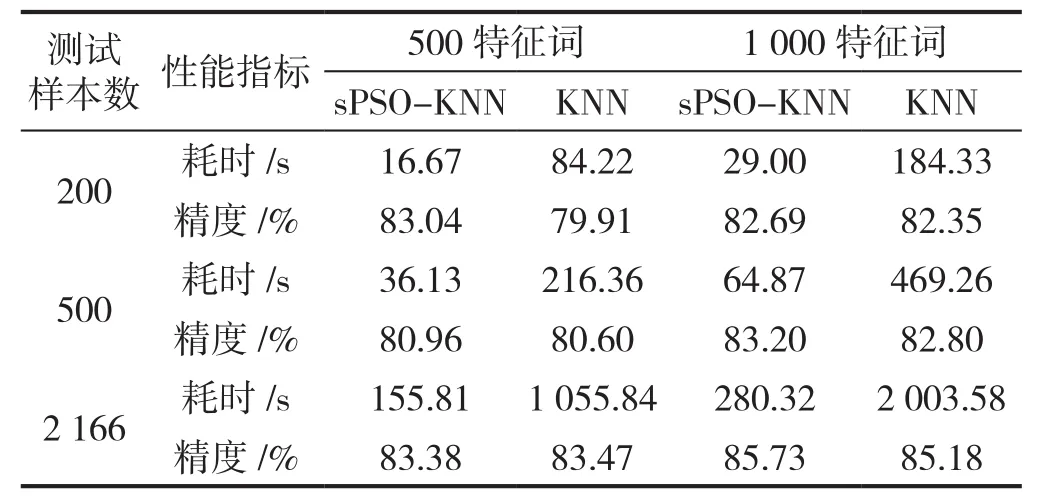
表2 实验结果统计数据

4 结语

利用粒子群优化算法进行组合优化，粒子的进化只针对样本的编号，而不涉及具体形式与取值，这种特性使粒子群算法非常适用于KNN算法的近邻搜索。虽然属于一种随机搜索策略，不能像利用不等式排除等全局最优搜索方法一样，得到的解一定为精确的k个近邻，但其搜索过程也是基于全局范围，有很大概率能够搜索到精确的k个近邻，对比实验也证明这种方法并未导致分类精度下降。粒子在个体最优pbest和群体最优gbest的指导下，能够尽快找到近邻样本，而不用与训练样本逐个比较，极大降低了计算开销，算法执行时间缩短80%以上，并且随着样本规模增大，效率的提升愈发显著。如何利用粒子群优化算法，在提高算法速度基础上，进一步实现分类精度的提高，是后续研究方向。

［1］ 奉国和.自动文本分类技术研究［J］.情报杂志，2007，26（12）：108-111.

［2］ YANG Y Y，LIU X.A re-examination of text categorization methods［C］//Hearst M，Gey F，Tong R.Proceedings of 22ndAnnual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York：ACM Press，1999：42-49.

［3］ COVER T M，HART P E.Nearest neighbor pattern classification［J］.IEEE Transactions on Information Theory，1967，IT13（1）：21-27.

［4］ 钱晓东，王正欧.基于改进KNN的文本分类方法［J］.情报科学，2005，23（4）：550-554.

［5］ RAYMER M L，PUNCH W E，GOODMAN E D，et al.Dimensionality reduction using genetic algorithms［J］.IEEE Transactions on Evolutionary Computation，2000，4（2）：164-171.

［6］ 李莹，张晓辉，王华勇，等.一种应用向量聚合技术的KNN中文文本分类方法［J］.小型微型计算机系统，2004，25（6）：993-996.

［7］ WILSON D L.Asymptotic properties of nearest neighbor rules using edited data［J］.IEEE Transactions on Systems，Man and Cybernetics，1972，SMC-2（3）：408-421.

［8］ HART P E.The condensed nearest neighbor rule［J］.IEEE Transactions on Information Theory.1968，14（3）：515-516.

［9］ 李荣陆，胡运发.基于密度的KNN文本分类器训练样本剪裁方法［J］.计算机研究与发展，2004，41（4）：539-545.

［10］ 鲁婷，王浩，姚宏亮.一种基于中心文档的KNN中文文本分类算法［J］.计算机工程与应用，2011，47（2）：127-130.

［11］ 吴春颖，王士同.一种改进的KNN Web文本分类方法［J］.计算机应用研究，2008，25（11）：3275-3277.

［12］ 张孝飞，黄河燕.一种采用聚类技术改进的KNN文本分类方法［J］.模式识别与人工智能，2009，22（6）：936-940.

［13］ 王煜，白石，王正欧.用于Web文本分类的快速KNN算法［J］.情报学报，2007，26（1）：60-64.

［14］ 乔玉龙，潘正祥，孙圣和.一种改进的快速k-近邻分类算法［J］.电子学报，2005，33（6）：1146-1149.

［15］ KENNEDY J，EBERHART R C.Particle swarm optimization［C］//IEEE.Proceedings of 1995 IEEE International Conference on Neural Networks.New York：IEEE，1995：1942-1948.

［16］ SHI Y H，EBERHART R C.Empirical study of particle swarm optimization［C］//IEEE.Proceedings of the 1999 Congress on Evolutionary Computation.New York：IEEE，1999：1945-1950.

［17］ OZCAN E，MOHAN C.Particle swarm optimization：surfing the waves［C］//IEEE.Proceedings of the 1999 Congress on Evolutionary Computation.New York：IEEE，1999：1939-1944.

［18］ EBERHART R C，SHI Y H.Particle swarm optimization：development，applications and resources［C］//IEEE.Proceedings of the 2001 Congress on Evolutionary Computation.New York：IEEE，2001：81-86.

［19］ YAMILLE D V，VENAYAGAMOORTHY G K，MOHAGHEGHI S，et al.Particle swarm optimization：basic concepts，variants and applications in powersystems［J］.IEEE Transactions on Evolutionary Computation，2008，12（2）：171-195.

［20］ 胡旺，李志蜀.一种更简化而高效的粒子群优化算法［J］.软件学报，2007，18（4）：861-868.

［21］ 张国英，沙芸，江慧娜.基于粒子群优化的快速KNN分类算法［J］.山东大学学报（理学版），2006，41（3）：34-36，42.

［22］ KENNEY J，EBERHART R C.A discrete binary version of the particle swarm algorithm［C］//IEEE.1997 IEEE international conference on systems，man，and cybernetics，computational cybernetics and simulation.New York：IEEE，1997：4104-4108.

［23］ LIANG Z G，GU X S，et al.A novel particle swarm optimization algorithm for permutation flow-shop scheduling to minimize makespan［J］.Chaos，solitons and fractals，2008，35（5）：851-861.

［24］ 中科院自动化所.以IG卡方等特征词选择方法生成的多维度ARFF格式中文VSM模型［EB/OL］.（2013-04-20）［2017-07-06］.http：//www.datatang.com/data/13485.

Research on the Improvement of KNN Algorithm Based on Particle Swarm Optimization

WU Jingxue
（School of Design，Shunde Polytechnic，Foshan Guangdong 528333，China）

In order to overcome the shortcomings of taking too much time in seraching for neighbors of the traditional KNN algorithm，this paper puts forward the particle swarm optimization algorithm to search for neighbors. Particles are initialized as the serial number of the k training samples，and in each iteration，an optimal individual pbest is defined as the set containing the current particle and the nearest neighbors searched by its previous pbest，and a group optimal gbest is defined as the set of nearest neighbors searched by current pbest. A distance index is used to avoid double counting. Contrastive experiments showed that the improved algorithm could shorten the time by more than 80%，without decreasing or even increasing the accuracy slightly.

KNN；particle swarm optimization；text categorization

TP301.6；G354

A

1672-6138（2017）04-0005-05

10.3969/j.issn.1672-6138.2017.04.002

2017-07-06

吴敬学（1986—），男，回族，河北承德人，硕士，研究方向：数据挖掘，经济信息分析。

曹娜］