解析AISC-89 ASD中K以及Lb对结构强度计算的影响
杨肖龙 李彦丽 安振武 祖 巍
(中海油能源发展装备技术有限公司 工程设计研发中心 天津300452)
解析AISC-89 ASD中K以及Lb对结构强度计算的影响
杨肖龙 李彦丽 安振武 祖 巍
(中海油能源发展装备技术有限公司 工程设计研发中心 天津300452)
AISC-89中明确了“ASD”法规定,即在工作载荷作用下,结构构件的应力不应超过规定的容许应力(即“容许应力法”,简称“ASD法”)。文中以容许应力法为基础,对海洋工程钢结构计算进行深入解读,归纳总结许用弯曲应力和许用压应力的计算方法,分析受压弯构件的有效长度系数K和侧向无支撑长度Lb对结构构件强度校核的影响,可供海洋工程钢结构设计参考。
容许应力法;海洋工程;结构设计;有效长度系数;侧向无支撑长度
引 言
作为世界上最具权威的钢结构设计规范,AISC自1923年问世以来获得了广泛应用。至今共推出两种不同的设计方法,即“容许应力法(ASD)”与“荷载和抗力分项系数设计法(LRFD)”。“ASD法”所基于的概念是:在正常工作载荷作用下结构部件中的最大应力不应超过规定的容许应力[1],容许应力是屈服应力除以安全系数,通过安全系数求得的容许应力的大小取决于起控制作用的特定极限状态,而安全系数是材料和所考虑构件的函数,仅依赖于传统经验。“LRFD法”是以统计方式分析各种荷载使材料破坏的概率,将各种荷载乘以不同的分项系数,作为应力需求,与材料实际的屈服强度比较判断是否安全。因此,“LRFD法”采用不同的分项系数,可以更精确地模拟不同荷载对结构强度的影响,计算方法更接近于实际,该方法在结构房屋建筑设计方面应用越来越广泛。
ANSI/AISC 360-10中也给出“ASD法”,但是该方法有别于传统的AISC-89版“ASD法”,而是将抗力系数和安全系数进行关联的简单方法,使“ASD法”与“LRFD法”具有相同的失效控制模式和承载 力 标准 值[2]。API RP 2A-WSD2014认 为 ANSI/AISC360-10版适用于钢框架房屋建筑设计,而对于海洋平台而言,其环境相对更加恶劣,基于保守考虑,API不推荐采用“LRFD法”,而是推荐采用AISC-89版“ASD法”[3]。目前,国内海洋平台的结构设计普遍沿用API RP 2A的推荐做法。国内,罗刚[4]对不同的钢结构设计方法进行详细的对比研究。
基于“ASD法”进行结构设计时,许用应力的计算是判断结构构件是否满足设计要求的基准,而构件的有效长度系数K和侧向无支撑长度Lb对许用应力的计算有直接影响。对于海洋平台立柱以及斜撑的设计,API RP 2A-WSD 2014已经有明确规定,本文主要探讨有效长度系数和侧向无支撑长度对受压I型或H型截面梁结构强度校核的影响。
1 截面类型定义
AISC根据截面尺寸将钢构件截面划分为紧凑型(Compact)、非紧凑型(Noncompact)和薄柔型(Slender)三种。该分类方法以构件受压截面的宽厚比为判断依据,AISC-89版定义了具体的划分依据,本文对部分常用构件的分类进行汇总和完善,见表1。
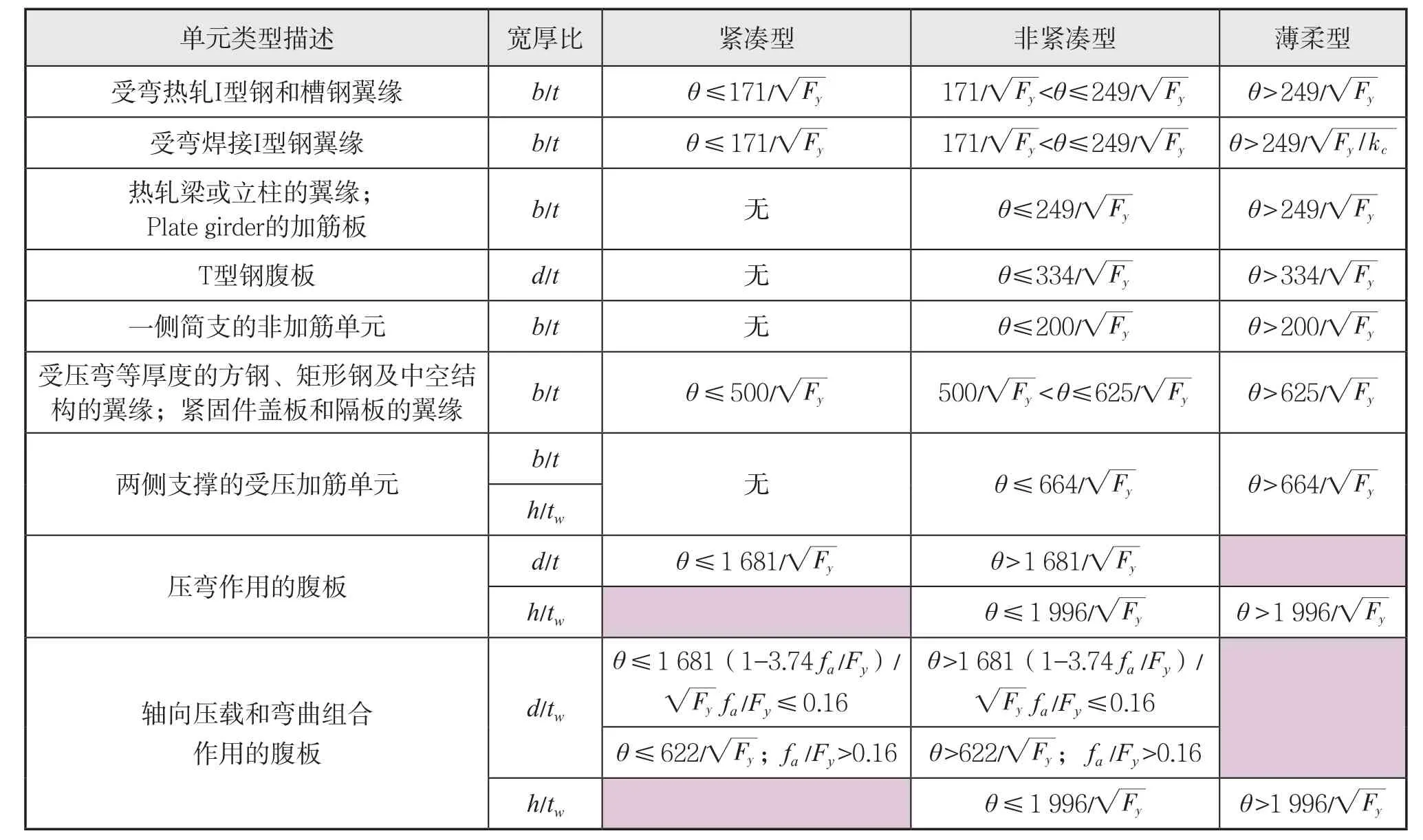
表1 受压构件截面单元宽厚比类型表
另外,AISC根据约束形式将构件截面分为加筋单元(Stiffened element)和非加筋单元(Unstiffened element)。加筋单元定义为沿力的方向两端有支撑的单元,例如I型、H型钢的腹板;非加筋单元定义为沿力的方向一端有支撑的单元,例如I型、H型钢翼缘的外伸枝、槽钢的翼缘等[5]。AISC根据构件截面的类型,规定了许用应力的不同计算方式。
2 许用压应力
2.1 规范分析
有效长度系数K,用于计算受压构件的许用压应力,Kl为等效长度,Kl/r称为长细比,是衡量构件刚度的标志,l为构件实际长度,r为构件截面回转半径,单位均为m。对于H型钢,K值按照截面方向可分为Ky、Kz,本文取一种进行分析。
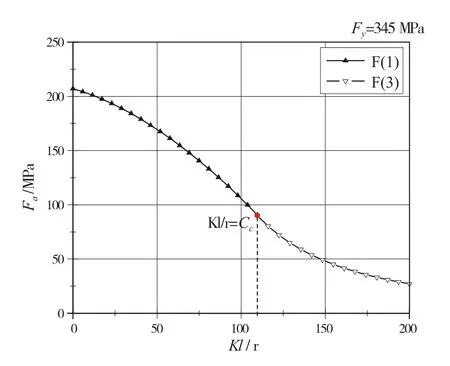
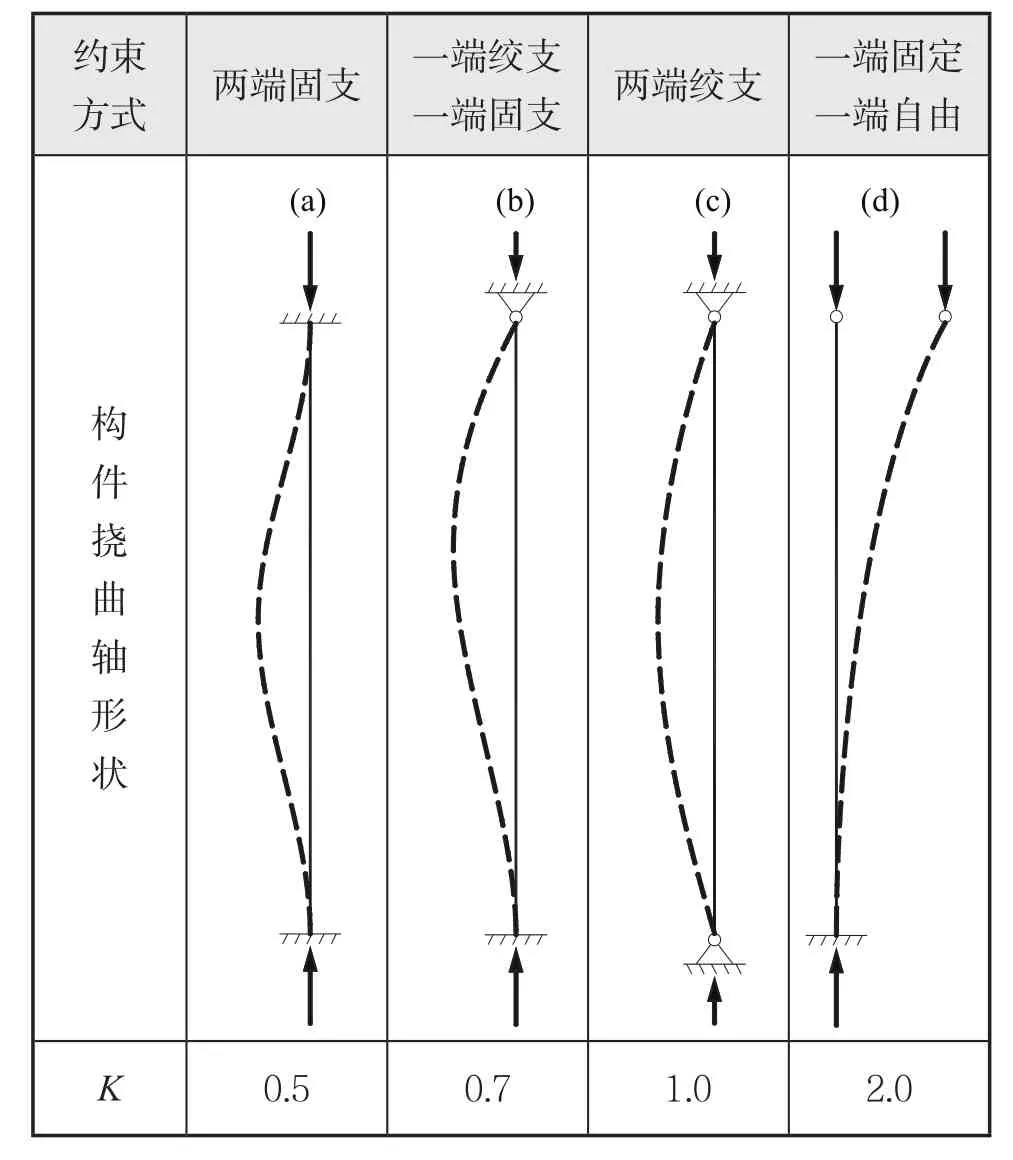
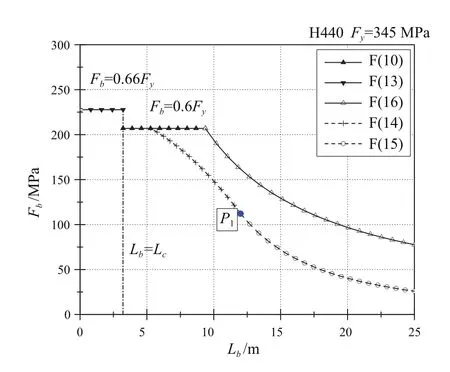
(1)对于紧凑型和非紧凑型截面,当Kl/r 式中:Fy为构件的屈服强度,MPa;Cc为构件整体屈曲判断标准,规定: 当Kl/r>Cc时,构件发生整体屈曲的临界载荷值小于使构件屈服的载荷值,因此以构件屈曲作为结构强度的判断依据,那么构件许用压应力为: (2)以上公式是针对紧凑和非紧凑截面,而对于含有薄柔型单元的构件,由于其结构特性需要考虑相应的折减系数。以H型钢为例,对于薄柔型截面,当时,受压构件许用压应力为: 当时,受压构件许用压应力为: 式中:b为非加筋受压单元宽度;t为非加筋单元厚度;Fy为屈服强度;当h/t>70,kc= 4.05/(h/t)0.46;其他情况,kc=1.0。 Qa为 加筋单元折减系数,Qa=Aeffective/Aactual,有效截面积Aeffective计算详见AISC(89版)附录B5.2。 从式(1)和式(3)可以看出,对于给定的某种材质的型钢,其屈服强度和弹性模量是确定的,那么受压构件的许用压应力只是长细比Kl/r的分段函数,对于H型钢,有强轴和弱轴之分,长细比取二者之间的较小值计算许用压应力。以JIS SM490YB材质的型钢为例,其屈服强度Fy=345 MPa,弹性模量E=2.06E5 MPa,其许用压应力随长细比的变化曲线如图1所示,Kl/r=Cc为分段函数的临界值。 图1 许用压应力曲线 从图中可以看出,受压构件的许用压应力随着长细比的增大显著降低,基于上述原因AISC对长细比给出明确的规定,对于受压构件长细比不能大于120,受拉构件长细比不能大于300。 有效长度Kl决定了构件许用压应力,有效长度系数K与构件端部约束有关,更准确地说,当无侧向支撑的构件受到足够大的轴向荷载时,其有效长度取决于其端部抵抗侧向位移的能力。显然,固支约束要强于绞支约束,绞支约束强于自由端,详见表2。 表2 不用约束方式的构件有效长度系数表 对于海洋工程中常见的平面框架结构,一般设计为纵横交错的主梁和次梁,这种结构不同于两端约束的简单构件,是一种空间结构体系。在结构计算中,需要考虑次梁是否对主梁的侧向变形产生影响。AISC给出门型框架结构立柱有效长度的系数计算经验公式: 式中:Ic和Lc分别为立柱的惯性矩和长度;Ig和Lg分别为立柱侧向支撑构件的惯性矩和长度。通过G值确定有效长度系数K值。G值越大,立柱侧向支撑构件对其约束能力越差,有效长度系数越大;反之,G值越小,立柱侧向支撑构件对其约束能力越强,有效长度系数越小。 以受压H440×300×11×18型钢为例,长度为2.0 m,屈服强度为345 MPa,假设有效长度系数为0.7,计算其许用压应力。 首先,判断型钢翼缘和腹板的截面单元特性,根据表1,受压I型钢翼缘判断公式计算如下: 翼缘:b/t=150/18=8.3,由表1可知临界值为故判断翼缘为紧凑单元。 腹板:H/tw= 404/11=36.7,由表 1可知临界值故判断腹板为薄柔型单元。 因此Qs=1,而腹板需考虑面积折减,Qa=Aeffective/Aactual=0.99。 根据截面尺寸可得弱侧回转半径rz=0.072 m,细长比Kl/r=19.5,Cc=106.97。 根据式(4),计算得到许用压应力Fa=195.6 MPa,根据API规范,结构实际压应力应与此值对比校核。 采用SACS软件结构强度分析,在水平层有主次分明的H型钢框架,对于受压主梁而言,如果侧向的支撑小梁对主梁翼缘的屈曲产生抵抗影响很小,那么需要对主梁的侧向无支撑强度进行修正。AISC规定侧向无支撑长度Lb作为计算H型钢强轴方向许用弯曲应力的判断依据。 首先,根据AISC规范,令 3.1.1 对于H型钢强轴受弯作用 (1)当Lb≤Lc时 对于紧凑型截面(翼缘板为紧凑型单元,不含Hybird beams和屈服强度高于450 MPa的构件) 困扰云服务行业的另一个问题是数据备份机制,以及存储在云中的信息究竟如何避免滥用或丢失的问题。这些企业是不能确保数据备份会存储在单独的磁带或者专门的设备上的。事实是,你的这些备份信息会与其他客户的数据一起存储在供应商可以负担得起的备份媒介上。可怕的是,你不会知道谁,何时,能够访问这些信息。 对于非紧凑型截面I(翼缘板为非紧凑型单元,腹板为紧凑单元) 对于非紧凑型截面II(翼缘板和腹板均为非紧凑型单元的Built-up members) 式中 :当h/tw>70,kc= 4.05 / (h/tw)0.46,否则kc= 1.0。 对于其他非紧凑型截面 (2)当Lb>Lc时 分为两种情况,第一种许用弯曲应力以l/rT值为界限进行区分。 第二种对于任意的l/rT: 从式(14)、式(15)和式(16)来看,对于给定结构形式的构件,其许用弯曲应力Fb是侧向无支撑长度l的单一函数,其中式(14)、式(15)是以l/rT值为界限的分段函数,式(16)为连续函数,通过这两种方式计算可以得到两条不同的函数曲线,许用弯曲应力取二者的较大值。 3.1.2 对于H型钢弱轴受弯作用 对于紧凑型对称截面 对于非紧凑型截面 以型钢H440×300×11×18和H800×300×16×25为例,长度l=2 m,其中H440屈服强度为345 MPa,H800屈服强度为550 MPa。分析在强轴受弯作用下不同侧向无支撑长度Lb对许用弯曲应力的影响。 对于H440型钢,根据式(9)计算得到Lc=3.22 m,以Lc为判断基准: (1)当Lb≤Lc,即侧向无支撑长度取值小于等于3.22 m,根据表1,公式计算H440翼缘为紧凑截面,许用弯曲应力应按照式(10)计算; (2)当Lb>Lc,许用弯曲应力应按照式(14)、式(15)和式(16)计算,取二者中较大值,且不超过0.6Fy。直观的分析,如图2所示,对于Lb>Lc的情况,按照式(14)、式(15)和式(16)计算的许用弯曲应力分别为图2中曲线F(14)、F(15)和曲线F(16),从图中可以看出按照式(16)计算的许用弯曲应力较大,应以此曲线作为不同Lb值时许用弯曲应力的取值,但不超过0.6Fy。 图2 H440许用弯曲应力曲线图 综上所述,图中实线(共3段)为许用弯曲应力随侧向无支撑长度Lb而变化的曲线。 对于H800型钢,根据式(9)计算得到,Lc= 2.35 m,以Lc为判断基准。 (1)当Lb≤Lc,即侧向无支撑长度取值小于等于2.35 m,根据表1公式计算H800翼缘为紧凑截面,许用弯曲应力应按式(10)计算; (2)当Lb>Lc,许用弯曲应力应按式(14)、式(15)和式(16)计算,取二者中较大值,且不超过0.6Fy。直观地分析(如图3所示),采用上述公式计算的许用弯曲应力有多个交叉点,所以H800型钢许用弯曲应力分为多段曲线。按式(14)、式(15)计算的许用弯曲应力分别为曲线F(14)和F(15),P2为分界点;按式(16)计算的许用弯曲应力为曲线F(16),其中曲线F(16c)代表的应力值大于式(14)、式(15)计算的应力值(P1和P3为分界点),但不超过0.6Fy。 图3 H800许用弯曲应力曲线图 综上所述,图3实线(共6段)为H800型钢许用弯曲应力随侧向无支撑长度Lb而变化的曲线。 本文以AISC-89版为基础,对海洋工程钢结构校核进行深入研究,重点分析钢结构许用压应力和许用弯曲应力计算的影响因素,总结为以下几点: (1)总结钢结构截面类型的分类和判断标准,以及截面类型的划分是结构许用应力计算的首要要素。 (2)根据理论计算分析受压构件有效长度系数K对结构许用压应力的影响,对于给定材质、截面类型的构件,其许用压应力只与构件的长细比有关。 (3)根据理论计算分析受弯构件的侧向无支撑长度Lb对结构许用弯曲应力的影响,对于给定材质、截面类型的构件,其许用弯曲应力只与侧向无支撑长度Lb有关,但判断条件较为复杂,表现为多区间函数。 综上所述,有效长度系数K和侧向无支撑长度Lb对许用弯曲应力的计算具有较大影响,海洋工程设计可根据结构特点并结合上述研究分析对有效长度系数K和侧向无支撑长度Lb进行合理地修正,以保证结构设计的可靠性与安全性。 [1] AISC. Manual of Steel Construction-Allowable Stress Design[S]. American Institute of Steel Construction,Inc,1989. [2] ANSI/AISC 360-10,Specification for Structural Steel Buildings[S]. American Institute of Steel Construction,Inc,2010. [3] API RP 2A,Planning, Designing, and Constructing Fixed Offshore Platforms-WSD[S]. American Petroleum Institute,2014. [4] 罗刚.中美钢结构基本构件安全度差异的比较分析[J].浙江建筑,2010(12):12-16. [5] 张庆芳,张志国.中外钢结构规范腹板有效宽度确定方法对比[J].钢结构,2008(5):45-48. [6] 王雪飞,王铁红,孙新.解读美标(AISC-ASD89)钢结构构件强度的计算方法[J].吉林建筑工程学院学报,2010(3):4-8. Influence of K and Lbon structural strength calculation based on AISC-89 ASD YANG Xiao-long LI Yan-li AN Zhen-wu ZU Wei In the AISC-89 ASD, the stress of the structural members under the working load should not exceed the allowable stress, which is called as allowable stress design and plastic design(ASD) method. The calculation of offshore engineering steel structure is then thoroughly interpreted based on the ASD method. The article summarizes the calculation methods of allowable bending stress, allowable compression stress, and analyzes the influence of the effective length factor K and the laterally unsupported length Lbof the compressed members on the structural strength calculation. It can provide reference for the design of offshore engineering steel structure. allowable stress design and plastic design(ASD); offshore engineering; structural design; effective length factor; laterally unsupported length U661.43 A 1001-9855(2017)06-0037-06 10.19423 / j.cnki.31-1561 / u.2017.06.037 2017-05-23; 2017-06-23 杨肖龙(1985-),男,硕士,工程师。研究方向:海洋工程结构设计。 李彦丽(1982-),女,硕士,工程师。研究方向:海洋工程结构设计。 安振武(1981-),男,硕士,工程师。研究方向:海洋工程结构设计。 祖 巍(1987-),男,工程师。研究方向:海洋工程结构设计。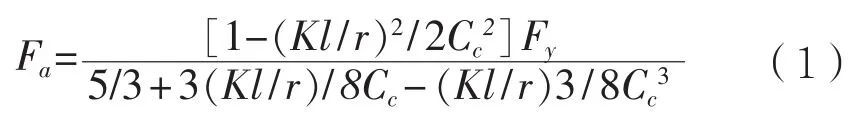
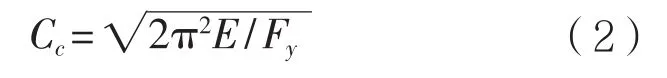
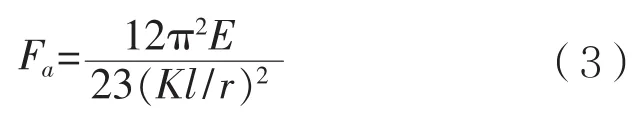
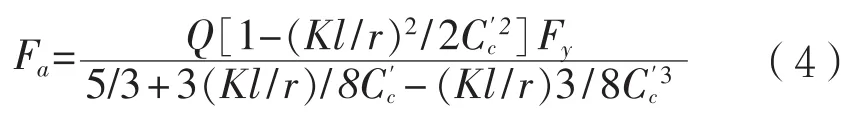

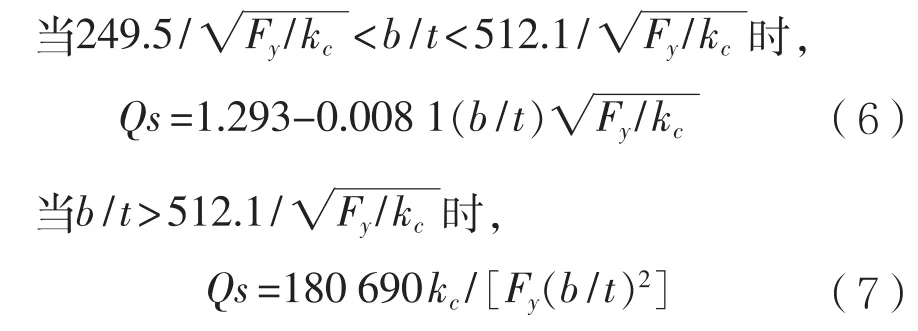
2.2 K值选取

2.3 算 例
3 许用弯曲应力
3.1 规范分析
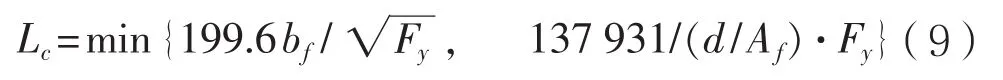

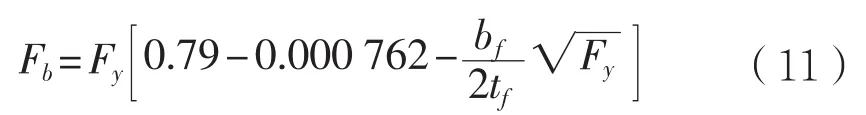
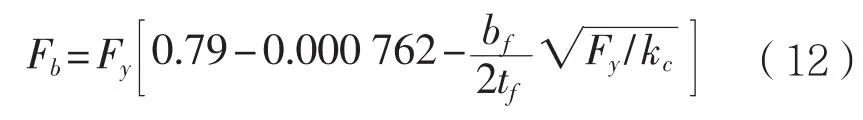





3.2 算 例

4 结 论
(CNOOC Ener Tech Equipment Technology Research & Design Center,Tianjin 300452, China)

