基于三次样条插值的非线性调频雷达信号设计

王侠,王进军,杨战社

(1.西安科技大学 电气与控制工程学院,陕西 西安 710054;2.陕西科技大学 电气与信息工程学院,陕西 西安 710021)

基于三次样条插值的非线性调频雷达信号设计

王侠1,王进军2,杨战社1

(1.西安科技大学 电气与控制工程学院,陕西 西安 710054;2.陕西科技大学 电气与信息工程学院,陕西 西安 710021)

在非线性调频雷达信号波形(NLFM)设计一般原理的基础上,以海明窗作为窗函数,利用三次样条插值法求反函数进行了NLFM信号波形设计,并对所设计的NLFM信号进行了脉冲压缩处理和matlab仿真,与传统的采用多项式拟合求反函数相比,三次样条插值法求得的结果误差更小,NLFM脉冲压缩波形的主副瓣比高达64.8dB。

非线性调频;雷达信号波形;三次样条插值;脉冲压缩

0 引言

脉冲压缩是现代雷达广泛采用的技术之一,它不但能提高雷达的分辨能力和检测能力,还能增强抗干扰能力,以满足雷达多功能、多模式的需要[1]。脉冲压缩雷达常用的信号有线性调频信号(LFM)和非线性调频信号(NLFM)。与LFM信号相比,NLFM信号的频率随时间非线性变化,它将LFM信号的加权网络转移分配在发射系统和接收系统中,不需要加权网络,从而有效避免了LFM信号采用失配技术加权处理所带来的信噪比损失[2]。

在NLFM信号设计中,信号波形和脉冲压缩滤波器的优化设计对提高脉冲压缩性能具有重要的意义, 传统的NLFM信号设计是在已知频谱结构的特殊窗函数的基础上,通过多项式拟合求反函数来完成[3],然而在实际的实验过程中,多项式拟合选用的拟合的阶数和理论值存在的偏差,使得NLFM信号波形存在一定的误差[4-5]。本文基于相位逗留原理,选用海明窗作为设计NLFM信号的窗函数,利用三次样条插值法求反函数进行了NLFM信号波形设计,并对设计的NLFM信号进行了脉冲压缩处理和分析, 与传统的多项式拟合求反函数相比,该方法求得的结果误差更小, NLFM脉冲压缩信号的副瓣抑制能力更强,该设计方法可广泛应用于非线性调频雷达信号波形的设计。

1 非线性调频雷达信号波形设计原理

假设所设计的NLFM信号为y(t)=exp(jφ(t)),其频谱函数为Y(f),则信号的距离-速度二维模糊函数为[6]:

(1)

根据信号的模糊函数设计NLFM信号波形,令ξ=0有:

(2)

如果使得信号的幅度谱|Y(f)|2具有某些特定窗函数的形式如W(f),相当于信号已经加窗,那么输出的信号波形的距离旁瓣将会被压低很多。通常选用的窗函数W(f)使信号幅度谱满足:

Y2(f)=W(f)

(3)

根据相位逗留原理[7]，可以求得信号的群时延T(f)为：

(4)

f(t)=T-1(f)

(5)

可得NLFM信号的相位函数:

(6)

最后根据相位函数求出所需的NLFM信号:

y(t)=exp(jφ(t))

(7)

2 三次样条插值的非线性调频雷达信号波形设计

在逗留相位原理的窗函数反求法基础上,采用三次样条插值法来设计NLFM信号的,具体流程如图1所示。

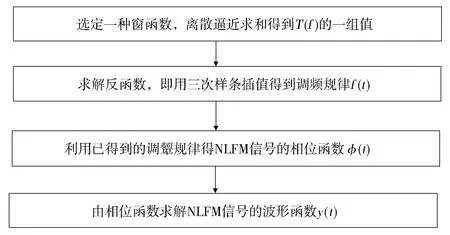
Fig.1 Implementation process of cubic spline interpolation图1 三次样条插值实现过程

2.1 NLFM信号群时延——频率关系求解

选用海明窗作为设计NLFM信号所需的窗函数,其函数表达式为[8-10]:

W(f)=0.54+0.46cos(2πf/B),f∈[-B/2,B/2]

(8)

将(8)代入(4)可得信号的群时延表达式为:

T(f)=0.54Kf+0.46K(B/2π)sin(2πf/B),f∈[-B/2,B/2]

(9)

T(f)=(T/B)f+(0.46/0.54)(T/2π)sin(2πf/B)

(10)

在f∈[-B/2,B/2]内,将频率f均匀化,对应每一个f,求出一个T(f)的值,这样就可以得到与海明窗函数对应的一组群时延(时间)和频率的值,带宽为10 MHz的T(f)-f的关系曲线如图2所示。

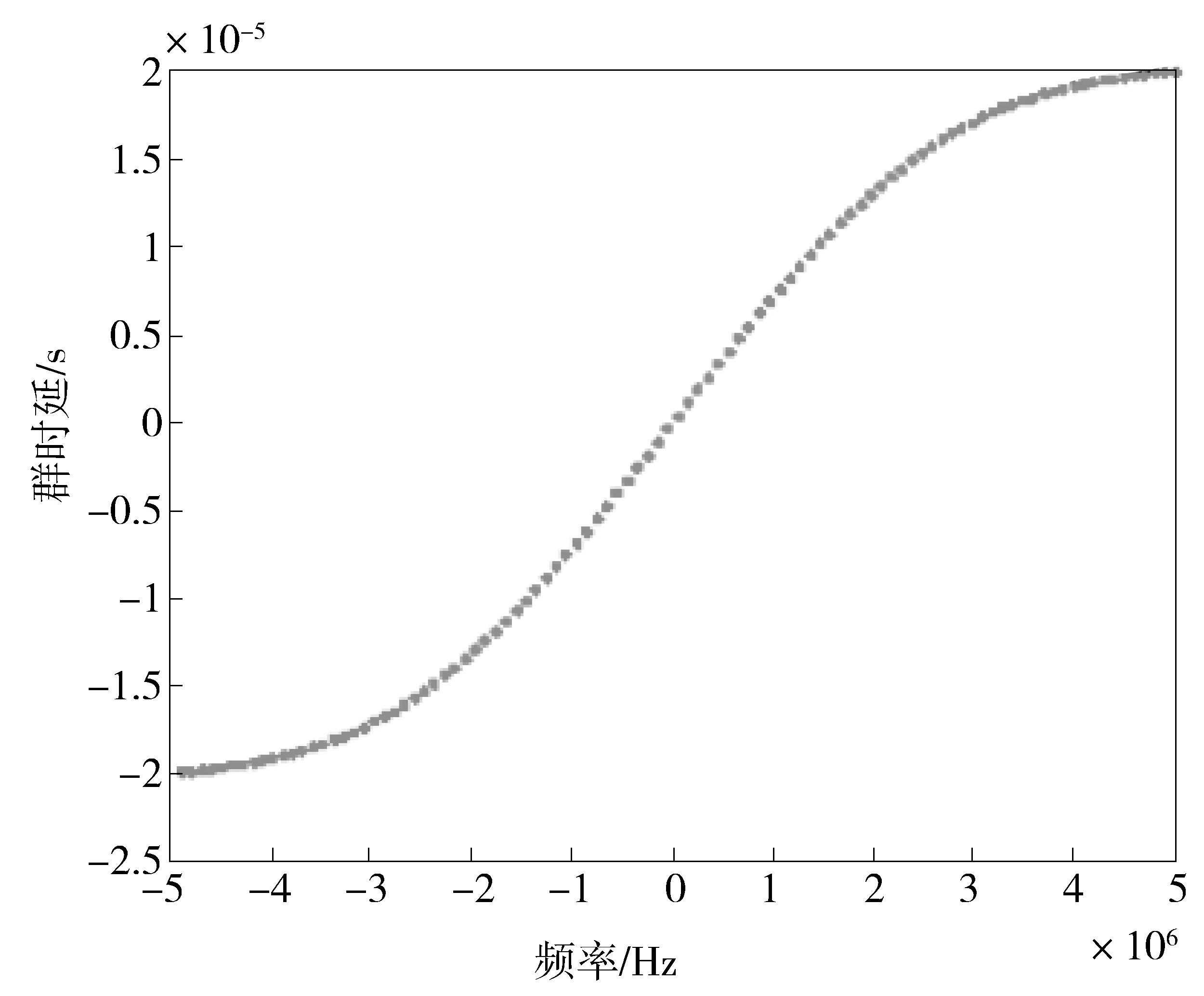
Fig.2 Group delay versus frequency curve of NLFM signal图2 NLFM信号群时延-频率曲线

2.2 三次样条插值计算

由图2所示的单调NLFM信号群时延-频率关系曲线可以看出,群时延T随着频率f的增加单调增加,所以群时延t=T(f)逆函数存在,假设NLFM频率-信号群时延的关系为f(t)=T-1(f)。对时间区间[a,b]进行n点等间隔划分,对于任意一个时迟ti都有一个频率样值fi=F(ti)(i=0,1,2,…，n)与其对应,根据三次样条插值原理,在每个小区间[ti-1,ti]构造三次样条插值函数s(t),根据三次样条插值函数的定义,则s(t)满足以下三个条件[11-12]:

(1)s(ti)=f(ti)=fi(i=0,1,…，n);

(2)在每个小区间[ti-1,ti],i=0,1,2，…，n上s(t)是不高过三次的多项式;

(3)在开区间(ti-1,ti)上s(t)有连续的二阶导数。

将s(t)在ti点做Taylor展开

(11)

由于s(t)在[ti,ti+1]上是三次多项式,则s″(t)在[ti,ti+1]上是一次多项式,设

s″(ti)=Mi(i=0,1,…，n)

(12)

则:

(13)

将(12)、(13)带入(11)得:

(14)

令(14)中t=ti+1,则:

(15)

考虑到s(ti+1)=F(ti+1)=fi+1, 带入(15),解得:

(16)

同理,在[xi-1,xi]区间解得:

(17)

可见,只要确定Mi(i=1,2,…，n),s′(ti)就可以确定, (14)给出的三次样条插值函数s(t)就可以确定。考虑到s′(ti)连续,所以(16)和(17)相等:

(18)

令hi=ti-ti-1,则hi+1=ti+1-ti,(18)可写为:

(19)

(20)

(21)

结合(19)、(20)、(21)就得到了关于Mi(i=0,1,2,…，n)的线性方程组

(22)

(22)中hi=ti-ti-1(i=1,2,…，n),只要从图2所示的NLFM信号群时延-频率曲线求出与每一时间点ti对应的频率值fi以及f′(t0)和f′(tn)就可以从(22)求解出Mi(i=0,1,2,…，n),代入(16)、(17)以及(14)进一步可以求出小区间[ti-1,ti]三次样条插值函数s(t),依次类推可以得到整个时间区间[a,b]上的NLFM信号的调频规律f(t)。

Matlab编程时,a=-2×10-5s,b=2×10-5s,n=100,f′(t0)=0,f′(tn)=0,采用三次样条插值法拟合得到的时宽为40 μs的调频规律如图3所示,与图4所示的拟合阶数为7的多项式拟合结果相比,三次样条插值拟合的结果更理想一些。这主要是因为三次样条插值函数不仅在各个节点处能能保证样本点和插值函数值相等,而且在节点的一阶微商处也相等,从而保证了拟合曲线的光滑性。而多项式拟合存在拟合的阶数问题,实际选用的拟合的阶数和理论值有差距时就会存在误差;而且多项式拟合是对整个曲线采用一个表达式,这也会带来一定的误差,从而导致拟合曲线的光滑性较差。

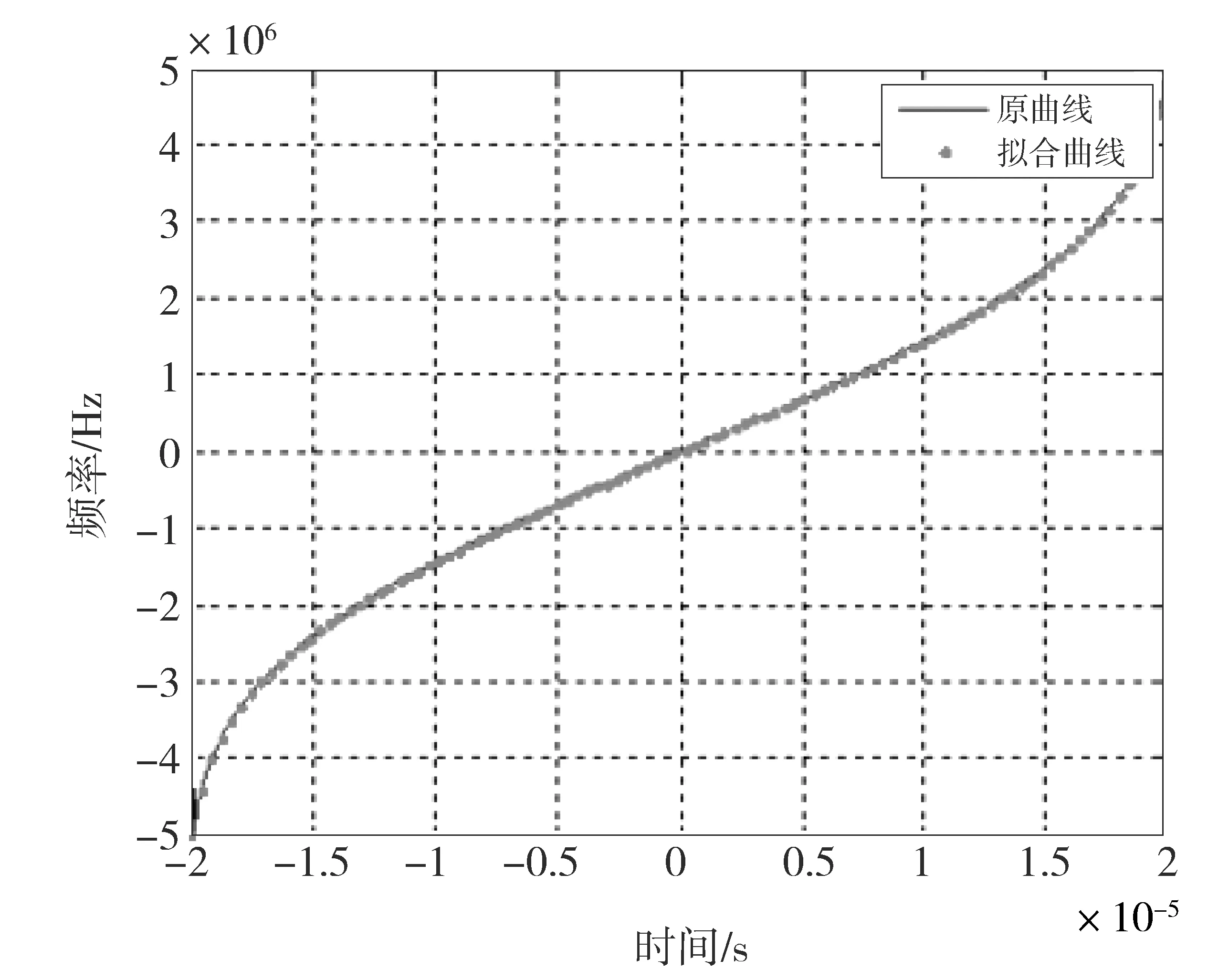
Fig.3 Time versus frequency curves obtained by cubic spline interpolation图3 三次样条插值求出的时间-频率关系曲线

Fig.4 Time versus frequency curves obtained by polynomial fitting图4 采用多项式拟合的时间-频率关系曲线

2.3 非线性调频雷达信号波形设计

将(14)三次样条插值函数s(t),依次代入(6)求出小区间[ti-1,ti]NLFM信号的相位函数φi(t),将所有小区间NLFM信号的相位函数φi(t)求和得到总的相位函数φ(t)=∑φi(t),matlab仿真结果如图5所示。

Fig.5 Phase curves of NLFM signals图5 NLFM信号的相位曲线

将相位函数φ(t)代入(7)求出NLFM信号y(t),y(t)实部与虚部随时间的变化曲线如图6所示,由图5、6可见信号频率随时间呈现非线性变化,即实现了非线性调频信号的初步设计。

Fig.6 Curves of real and imaginary parts of NLFM signals图6 NLFM信号实部和虚部的变化曲线

3 NLFM信号的脉冲压缩

采用匹配滤波对所设计的NLFM信号的进行脉冲压缩处理, 将雷达天线和目标看作一个LTI(线性时不变)系统,如图7所示[13-15],匹配滤波在时域对脉冲压缩进行处理,实质就是雷达回波序列s(k)与匹配滤波器的系数序列h(k)做复数卷积运算[16-17]:

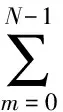
(23)

Fig.7 Matched filtering of NLFM signals图7 NLFM信号的匹配滤波

以时间宽度T=200 μs,带宽B=4 MHz,采用海明窗函数进行设计的NLFM信号,NLFM信号经匹配滤波处理后得到的三次样条插值NLFM信号脉冲压缩波形matlab仿真结果如图8所示。由图8可以看出,NLFM脉冲压缩波形的主副瓣比高达64.8 dB。

图9为采用多项式拟合NLFM信号脉冲压缩波形,比较图8和图9可以看出与传统的采用多项式拟合求反函数相比,三次样条插值法求得的NLFM脉冲压缩波形的主副瓣比更高,这是由于三次样条插值法拟合误差小,而多项式拟合存在拟合的阶数问题,拟合误差较大,从而使得NLFM脉冲压缩波形的主副瓣比降低。

Fig.8 Pulse compression waveform of cubic spline interpolation NLFM signals图8 三次样条插值NLFM信号脉冲压缩波形

Fig.9 Pulse compression waveform of polynomial fitting NLFM signals图9 多项式拟合NLFM信号脉冲压缩波形

针对基于多项式拟合的非线性调频(NLFM)雷达信号波形由于拟合阶数和理论值存在的偏差带来的误差大的缺点,本文基于逗留相位原理,选用海明窗作为设计NLFM信号的窗函数,利用三次样条插值法求反函数进行了NLFM信号波形设计,详细介绍了三次样条插值法由信号群时延-频率关系曲线拟合调频规律f(t)的过程,并对所设计的NLFM信号进行了脉冲压缩处理和分析,与传统的采用多项式拟合求反函数相比,三次样条插值法求得的结果误差更小;最后对设计得到的NLFM信号进行了脉冲压缩处理,给出了NLFM信号脉冲压缩matlab仿真的波形, NLFM脉冲压缩信号具有较高的副瓣抑制能力,该设计方法可广泛应用于非线性调频雷达信号波形的设计。

[1] 张群英,何佩琨,毛二可.一种改进的非线性调频信号波形设计方法[J].北京理工大学学报,2000,20(3):352-355.DOI:10.3969/j.issn.1001-0645.2000.03.020.

[2] Pan Y,Peng S,Yang K,etal.Optimization Design of NLFM Signal and Its Pulse Compression Simulation[C]∥Radar Conference,2005 IEEE International，2005:383-386.DOI:10.1109/RADAR.2005.1435855.

[3] Dantas T M,Costa-Felix R P B,Machado J C.Improved Range Resolution and Side Lobe Level of Ultrasound Echoes using Nonlinear Frequency-modulated Excitation Signal and Modified Compressing Filter[C]∥Ultrasonics Symposium.IEEE.2012:1439-1442.DOI:10.1109/ULTSYM.2011.0356.

[4] 鲍坤超,陶海红,廖桂生.基于多项式拟合的非线性调频波形设计[J].信号处理,2008,24(2):189-191.DOI:10.3969/j.issn.1003-0530.2008.02.006.

[5] Luo F,Liting R,Wu S,etal.Design of Modified Spectrum Filter based on Mismatched Window for NLFM Signal[C]∥Synthetic Aperture Radar,2009.Apsar 2009.Asian-Pacific Conference on.IEEE,2009:274-277.DOI:10.1109/APSAR.2009.5374149.

[6] 何学辉,陶海红,吴兆平,等.一种改进的非线性调频信号设计[J].电子学报,2009,37(8):1784-1788.DOI:10.3321/j.issn:0372-2112.2009.08.028.

[7] Hussain Z M,Boashash B.Adaptive Instantaneous Frequency Estimation of Multicomponent FM Signals Using Quadratic Time—Frequency Distributions[J].IEEETransactionsonSignalProcessing,2002,50(8):1866-1876.DOI: 10.1109/TSP.2002.800406.

[8] 张民,刘海鹏,蔡兆晖.基于组合窗的 OFDM-NLFM 信号设计[J].系统工程与电子技术,2016(2):287-292.DOI:10.3969/j.issn.1001-506X.2016.02.08.

[9] 刘春冉,陈伯孝,李锋林.基于窗函数的非线性调频信号的设计和性能分析[J].火控雷达技术,2007,36(3):78-83.DOI:10.3969/j.issn.1008-8652.2007.03.016.

[10] Vizitiu I,Anton L,Popescu F,etal.The Synthesis of Some NLFM Laws Using the Stationary Phase Principle[C]∥International Symposium on Electronics and Telecommunications，2012:377-380.DOI:10.1109/ISETC.2012.6408053.

[11] 王萱芬,李巍,王子立.一种实现超低旁瓣的脉冲压缩算法[J].现代电子技术,2009,32(23):5-7.DOI:10.3969/j.issn.1004-373X.2009.23.002.

[12] Yue W,Zhang Y.A Novel Nonlinear Frequency Modulation Waveform Design Aimed at Side-lobe Reduction[C]∥IEEE International Conference on Signal Processing,Communications and Computing.IEEE,2014:613-618.DOI: 10.1109/ICSPCC.2014.6986266.

[13] 刘萍,邹林,周云,等.基于NLFM的超低旁瓣脉冲压缩方法研究[J].雷达科学与技术,2014(5):527-531.DOI:10.3969/j.issn.1672-2337.2014.05.014.

[14] 彭志刚,杨志国,彭世蕤.一种非线性调频信号数字脉压性能分析[J].空军预警学院学报,2003,17(3):51-53.DOI:10.3969/j.issn.1673-8691.2003.03.017.

[15] Kurdzo J M,Cheong B L,Palmer R D,etal.Optimized NLFM Pulse Compression Waveforms for High-Sensitivity Radar Observations[C]∥International Radar Conference,2014:1-6.DOI: 10.1109/RADAR.2014.7060249.

[16] Witte E D,Griffiths H D.Improved Ultra-low Range Sidelobe Pulse Compression Waveform Design[J].ElectronicsLetters,2004,40(22):1448-1450.DOI:10.1049/el:20046548.

[17] 付启众,陈忠先.一种超低副瓣非线性调频脉压信号的性能分析[J].雷达科学与技术,2007,5(1):60-64.DOI:10.3969/j.issn.1672-2337.2007.01.012.

NonlinearFrequency_modulationRadarSignalDesignBasedontheCubicSplineInterpolated

WANG Xia1,WANG Jinjun2,YANG Zhanshe1

(1.CollegeofElectricalandControlEngineering,Xi’anUniversityofScience&Technology,Xi’an710054,China;2.CollegeofElectricalandInformationEngineering,ShannxiUniversityofScience&Technology,Xi’an710021,China)

Based on the general design principle of nonlinear frequency modulated radar signal waveform (NLFM), Hamming window was chosen as the window function to design nonlinear frequence modulation(NLFM) radar signal by using the cubic spline interpolation method to solve the inverse function, the designed NLFM radar signal has been pulsed compression and the pulse compression waveform was simulated using matlab,the results obtained by Cubic spline interpolation method has smaller error than the results obtained by polynomial fitting to solve the inverse function and the main-to-side lobe ratio of NLFM pulse compression waveform reaches up to 64.8 dB.

nonlinear frequency_modulation;radar signal waveform;cubic spline interpolated;pulse compression

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.019

2016-06-05；

2017-03-28

陕西省2015年科学技术研究与发展计划项目(2015GY081)

王侠(1979-),女,陕西杨凌人,硕士,讲师,主要从事信息与控制方面的研究。E-mail:wang98415123@163.com

TN957.51

A

0253-2395(2017)04-0797-07