两个正态随机变量分布参数的比较

刘小宁 刘 兵 杨 帆 吴元祥 刘 岑 张 磊

(1.武汉软件工程职业学院 机械工程学院 湖北 武汉：430205；2.湖北轻工职业技术学院 机电工程学院 湖北 武汉：430070)

两个正态随机变量分布参数的比较

刘小宁1刘 兵1杨 帆1吴元祥1刘 岑2张 磊1

(1.武汉软件工程职业学院 机械工程学院 湖北 武汉：430205；2.湖北轻工职业技术学院 机电工程学院 湖北 武汉：430070)

为了比较两个正态分布随机变量分布参数大小，应用概率论与数理统计知识，建立了一种直接方法。在双侧置信度为99%时，根据奥氏体不锈钢S30408在不同状态的拉伸试验数据，分别比较与评价了其屈服强度与抗拉强度分布参数的大小。从室温降至液氮温度，对于非预应变奥氏体不锈钢S30408，屈服强度的均值与标准差同时显著增大；抗拉强度的均值显著增大，标准差没有显著变化。在液氮温度时，与非预应变相比，9%预应变奥氏体不锈钢S30408钢屈服强度的均值显著增大，抗拉强度的均值、以及屈服强度与抗拉强度的标准差均没有显著变化。

分布参数；比较；直接方法；正态分布；随机变量

均值与标准差是描述正态随机变量特征的分布参数，均值反映正态分布中心位置，标准差反映正态分布的离散性。在均值不变时，标准差小，表明数据相互偏离小，集中性好；标准差大，表明数据相互偏离大，集中性差。在工程实际中，经常遇见符合正态分布的同一物理量在不同状态时的分布参数比较问题，例如，深冷压力容器在常温制造，在液氮温度(-196℃)使用，根据不同状态时的材料拉伸试验数据，分析屈服强度与抗拉强度的均值与标准差变化，是进行其强度设计的重要基础工作之一[1]。

对于两个符合正态分布的随机变量，目前采用t分布假设检验比较其均值的大小，采用F分布假设检验比较其标准差的大小[1-10]，但是该方法似存在如下两个问题：其一，假设两个正态随机变量标准差相等，是利用t分布假设检验比较两个均值大小的前提；其二，如果标准差不相等，两个均值比较变化为贝伦斯-费歇问题，假设检验方法无法直接应用。

为此，文中基于概率论与数理统计知识，建立了比较与评价两个正态随机变量分布参数大小关系的直接方法；根据奥氏体不锈钢S30408在不同状态的拉伸试验数据[11-13]，分别比较与评价了屈服强度与抗拉强度分布参数的大小。

1 基本理论与方法

为了讨论方便，假设物理量R的分布参数是需要比较的研究对象，在A与B状态时，与R对应的随机变量RA与RB基本符合正态分布，RA与RB的均值分别为μA与μB，标准差分别为σA与σB。

分布参数的比较是指均值μA与μB的比较，或者是指标准差σA与σB的比较。从工程实践的角度，μA与μB或者σA与σB是未知的，从概率论与数理统计知识，可以通过RA与RB的有效试验值，得到分布参数的取值区间，再进行分布参数比较。

1.1 RA分布参数的取值区间

在A状态通过试验获得RA的p组有效试验数据RAi(i=1，2，…，p)，RA样本的平均值与精密度分别为：

(1)

(2)

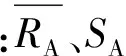
1.1.1μA的取值区间

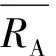
μAmin≤μA≤μAmax

(3)

其中

(4)

(5)

式中：μAmin与μAmax分别为μA在双侧置信度为(1-α)时的下限与上限；tp-1,1-0.5α为t分布系数，由自由度(p-1) 与双侧置信度(1-α)查得。

双侧置信度(1-α)中的α，此处是指将满足式(3)的μA，误判为μA<μAmin与μA>μAmax的风险概率各为0.5α。

工程上取α=0.01[1]，文中所用t分布系数见表1[14]。

表1 t分布系数

1.1.2σA的取值区间

SA是RA标准差σA的无偏估计，在双侧置信度为(1-α)时，σA的取值区间[1-3]为：

σAmin≤σA≤σAmax

(6)

其中

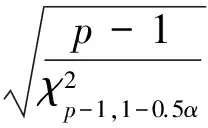
(7)

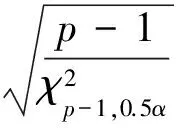
(8)

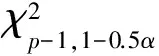
双侧置信度(1-α)中的α，此处是指将满足式(6)的σA，误判为σA<σAmin与σA>σAmax的风险概率各为0.5α。

表2 χ2分布系数

1.2 RB分布参数的取值区间

1.2.1μB的取值区间

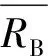
μBmin≤μB≤μBmax

(9)

此处双侧置信度(1-α)中的α，是指将满足式(9)的μB，误判为μB<μBmin与μB>μBmax的风险概率各为0.5α。

1.2.2σB的取值区间

SB是RB标准差σB的无偏估计，在双侧置信度为(1-α)时，对式(7)与式(8)作变换A→B及p→q，可得到σB的下限σBmin与上限σBmax；因此，σB的取值区间为[1-3]：

σBmin≤σB≤σBmax

(10)

此处双侧置信度中的α，是指将满足式(10)的σB，误判为σB<σBmin与σB>σBmax的风险概率各为0.5α。

1.3 μA与μB之间关系的判据

双侧置信度为(1-α)时，由式(3)与式(9)可得

μAmin-μBmax≤μA-μB≤μAmax-μBmin

(11)

由式(11)可知μA显著大于μB的表征：

μAmin-μBmax>0

(12)

μA显著小于μB的表征由式(11)可得：

μAmax-μBmin<0

(13)

μA-μB≈0是μA与μB无显著差异的充分必要条件，由式(11)可得μA与μB无显著差异的表征：

μAmin-μBmax≤0≤μAmax-μBmin

(14)

为了讨论方便，记

(15)

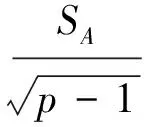
(16)

1.3.1μA显著大于μB的判据

将式(4)的μAmin与作变换得到的μBmax代入式(12)，结合式(15)与式(16)，可得到μA显著大于μB的判据：

δ>δ1

(17)

1.3.2μA显著小于μB的判据

将式(5)的μAmax与作变换得到的μBmin代入式(13)，结合式(15)与式(16)，可得到μA显著小于μB的判据：

δ<-δ1

(18)

1.3.3μA与μB无显著差异的判据

将μAmin与μBmax、μAmax与μBmin代入式(14)，结合式(15)与式(16)，可得μA与μB无显著差异的判据：

-δ1<δ<δ1

(19)

与t假设检验方法[1-6]相比，文中建立的比较与评价两个均值大小的直接方法，不需要假设两个正态随机变量的标准差相等，具有简便的特点。

1.4 σA与σB之间关系的判据

在双侧置信度为(1-α)时，根据式(6)与式(10)可得：

σAmin-σBmax≤σA-σB≤σAmax-σBmin

(20)

由式(20)可得σA显著大于σB的表征：

σAmin-σBmax>0

(21)

根据式(20)，σA显著小于σB的表征：

σAmax-σBmin<0

(22)

σA与σB无显著差异的表征为σA-σB≈0，根据式(20)可得到

σAmin-σBmax≤0≤σAmax-σBmin

(23)

为了讨论方便，记

(24)

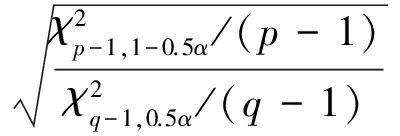
(25)

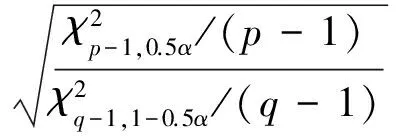
(26)

1.4.1σA显著大于σB的判据

将式(7)的σAmin与作变换得到的σBmax代入式(21)整理，并结合式(24)与式(25)，可得到σA显著大于σB的判据

λ>λ1

(27)

1.4.2σA显著小于σB的判据

将式(8)的σAmax与作变换得到的σBmin代入式(22)整理，并结合式(24)与式(25)，可得到σA显著小于σB的判据：

λ<λ2

(28)

1.4.3σA与σB无显著差异的判据

将σAmin与σBmax、σAmax与σBmin代入式(23)整理，并结合式(24)～式(26)，得到σA与σB无显著差异判据：

λ2<λ<λ1

(29)

与F假设检验方法[1-6]相比，文中建立的比较与评价两个正态随机变量标准差大小的直接方法，不需要先假设后检验，具有简便的特点。

2 实例

奥氏体不锈钢S30408是深冷容器用钢，深冷容器往往在室温制造，在液氮温度(-196℃)使用。为了在保证容器安全的同时节约钢材，研究提高钢材许用应力的方法是目前的前沿与热点课题，例如有关文献[11-13]认为，9%预应变在不改变奥氏体不锈钢S30408抗拉强度时，可提高的其屈服强度，达到提高钢材许用应力的目的。因此，研究温度变化及9%预应变对奥氏体不锈钢S30408抗拉强度与屈服强度分布参数的定量影响，是值得探讨的内容。

基于非预应变与9%预应变奥氏体不锈钢S30408液氮温度抗拉强度基本符合正态分布的研究[16-19]，在其他状态时，文中假设奥氏体不锈钢S30408抗拉强度与屈服强度均是基本符合正态分布的随机变量。

在试验数据的双侧置信度为99%时，非预应变S30408钢室温与液氮温度抗拉强度与屈服强度的有效试验数据[11-13]及其统计，分别见表3与表4；9%预应变S30408钢液氮温度抗拉强度与屈服强度的有效试验数据[11-13]及其统计见表5。

表3 室温非预应变S30408钢有效试验数据统计

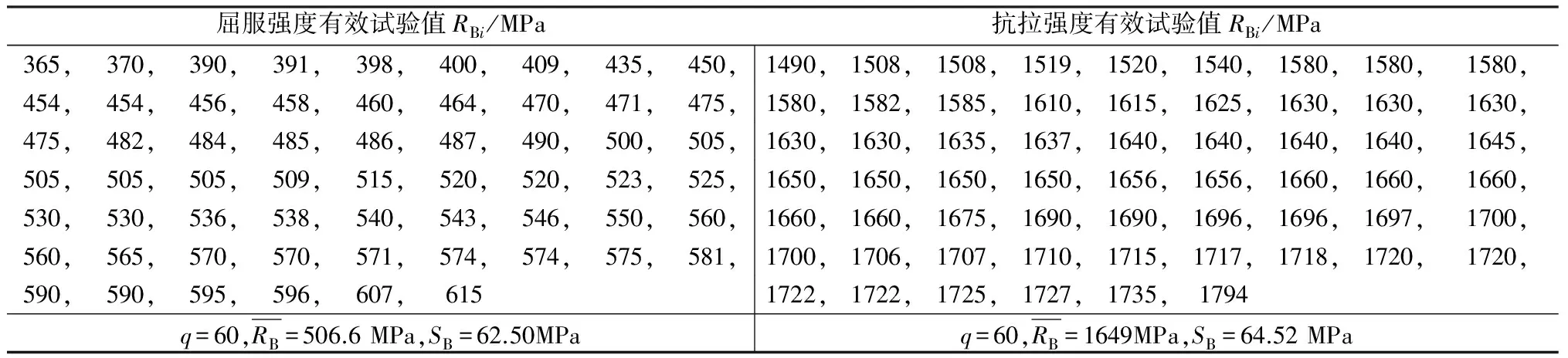
表4 液氮温度非预应变S30408钢有效试验数据统计

2.1 温度变化对非预应变奥氏体不锈钢的影响

将室温与液氮温度分别定义为A与B状态；双侧置信度为99%时，比较温度变化对非预应变奥氏体不锈钢S30408屈服强度与抗拉强度分布参数的影响。

表5 液氮温度9%预应变S30408钢的有效试验数据统计

2.1.1 对屈服强度分布参数的影响

1)均值。根据表3与表4中的统计数据，由式(15)与式(16) 可得：δ=-190.6，δ1=44.53；因为δ<-δ1满足式(18)，即μA<μB是显著的，因此，非预应变奥氏体不锈钢S30408从室温降至液氮温度时，其屈服强度均值显著增大。

2)标准差。根据表3与表4中的统计数据，由式(24)～式(26)可得：λ=0.1589，λ1= 2.5107，λ2=0.1835；因为λ<λ2满足式(28)，即σA<σB是显著的，因此，非预应变奥氏体不锈钢S30408从室温降至液氮温度时，其屈服强度标准差增大显著。

从室温降至液氮温度，非预应变奥氏体不锈钢S30408屈服强度标准差显著增大，虽然不能用t分布假设检验的方法[2-3]比较其均值的大小关系，但是，利用文中建立的方法，可直接比较两个均值的大小。

2.1.2 对抗拉强度分布参数的影响

1)均值。根据表3与表4中的统计数据，由式(15)与式(16)得到：δ=-881.3，δ1=55.99；因为δ<-δ1满足式(18)，即μA<μB是显著的，因此，非预应变奥氏体不锈钢S30408从室温降至液氮温度时，其抗拉强度均值显著增大。

2)标准差。根据表3与表4中的统计数据，由式(24)～式(26)可得到：λ=0.2264，λ1= 2.5107，λ2= 0.1835；因为λ2<λ<λ1满足式(29)，说明σA与σB无显著差异，因此，非预应变奥氏体不锈钢S30408从室温降至液氮温度时，其抗拉强度标准差无显著变化。

双侧置信度为99%时，以上分析表明，将非预应变奥氏体不锈钢S30408的温度从室温降至液氮温度，可显著提高其屈服强度与抗拉强度的均值，但是屈服强度的标准差显著增大，存在降低屈服强度精度的危险，这一点必须引起工程界的足够重视。

2.2 9%预应变对液氮温度奥氏体不锈钢的影响

将9%预应变与非预应变分别定义为A与B状态；双侧置信度为99%时，比较9%预应变对液氮温度奥氏体不锈钢S30408屈服强度与抗拉强度标准差的影响。

2.2.1 对屈服强度分布参数的影响

1)均值。根据表5与表4中的统计数据，由(15)与式(16)得到：δ=58.1，δ1=42.63；因为δ>δ1满足式(17)，即μA>μB是显著的，因此，9%预应变显著提高了奥氏体不锈钢S30408液氮温度屈服强度的均值。

2)标准差。根据表5与表4中的统计数据，由式(24)～式(26)可得：λ=0.7955，λ1= 1.6782，λ2=0.5829；因为λ2<λ<λ1满足式(29)，说明σA与σB无显著差异，因此，9%预应变对奥氏体不锈钢S30408液氮温度屈服强度的标准差无显著影响。

2.2.2 对抗拉强度分布参数的影响

1)均值。根据表5与表4中的统计数据，由(15)与式(16)得到：δ=3.00，δ1=45.01；因为-δ1<δ<δ1满足式(19)，说明μA与μB无显著差异，因此，9%预应变对奥氏体不锈钢液氮温度抗拉强度均值基本无影响。

2)标准差。根据表5与表4中的统计数据，由式(24)～式(26)得到：λ=0.8321，λ1= 1.6782，λ2= 0.5829；因为λ2<λ<λ1满足式(29)，说明σA与σB无显著差异，因此，9%预应变对奥氏体不锈钢S30408液氮温度抗拉强度的标准差无显著影响。

双侧置信度为99%时，根据以上分析，9%预应变对奥氏体不锈钢S30408液氮温度屈服强度与抗拉强度的标准差无显著影响，是显著提高液氮温度屈服强度均值的有效方法，值得工程界重视。

3 结论

1)对于两个符合正态分布随机变量，文中应用概率论与数理统计知识，建立了比较与评价其分布参数大小关系的直接方法，不但拓广了目前假设检验方法的应用范围，而且具有简便的特点。根据奥氏体不锈钢S30408在不同状态的拉伸试验数据，双侧置信度为99%时，分别比较了其屈服强度与抗拉强度分布参数的大小。

2)当非预应变奥氏体不锈钢S30408钢从室温降至液氮温度时，屈服强度的均值与标准差同时显著增大；抗拉强度的均值显著增大，但标准差没有显著变化。

3)在液氮温度时，与非预应变相比，9%预应变奥氏体不锈钢S30408钢屈服强度的均值显著增大，抗拉强度的均值、以及屈服强度与抗拉强度的标准差均没有显著变化。

4)9%预应变方法，对奥氏体不锈钢S30408液氮温度屈服强度与抗拉强度的标准差无显著影响，并且有效提高了液氮温度屈服强度的均值，值得工程界重视。

5)尽管从室温降至液氮温度的方法，可显著提高非预应变奥氏体不锈钢S30408屈服强度与抗拉强度的均值，但是屈服强度的标准差也显著增大，必须引起工程界的足够重视。

[1] 徐灏.机械强度的可靠性设计[M].北京:机械工业出版社,1984:39-55.

[2] 熊德之,张志军.概率论与数理统计及其应用[M].北京:科学出版社,2007:130-138,151-153.

[3] 化学工程手册编辑委员会.化工应用数学[M].北京:化学工业出版社,1983:371-375.

[4] 刘小宁,刘岑,刘兵,等.屈强比对容器爆破压力计算公式精度的影响[J].应用力学学报,2017,34(1):141-147.

[5] 刘小宁,刘岑,张红卫,等.对“基于实测数据的特种球形压力容器爆破压力计算公式”一文的商榷[J].应用数学和力学,2016,37(5):552-550.

[6] 刘岑,袁小会,刘兵,等.钢制单层球形容器爆破压力的计算[J].武汉工程大学学报,2016,38(3):299-306.

[7] 刘小宁,刘岑,吴元祥,等.超高压圆筒容器爆破压力计算公式的比较[J].机械强度,2015,37(2):373-376.

[8] 刘小宁,刘岑,刘兵,等.单层厚壁内压圆筒设计公式改进效果的可靠性研究[J].机械强度,2016,38(2):276-283.

[9] 杨帆,刘岑,刘兵,等.铜管爆破压力计算公式[J].武汉工程职业技术学院学报,2017,29(3):12-16.

[10] 刘小宁，刘岑，刘兵，等.承压容器爆破压力计算公式的评价方法与研究[J].机械强度，2017，39(6)：1409-1417.

[11] 郑津洋,王珂,黄泽,等.液氮温度下奥氏体不锈钢强度试验研究[J].压力容器,2014,31(8):1-6.

[12] 刘凡,江楠,张文建,等.国产奥氏体不锈钢06Cr19Ni10(S30408)拉伸试验研究[J].压力容器,2011,28(4):7-11.

[13] 黄泽,缪存坚,李涛,等.预拉伸奥氏体不锈钢常温拉伸力学性能试验研究[J].压力容器,2013,30(6):7-11.

[14] GB 4086.3-83,统计分布数值表t分布[S].

[15] GB 4086.2-83,统计分布数值表χ2分布[S].

[16] 李清,袁小会,刘岑,等.有效试验数据对钢材机械性能分布规律的影响[J].武汉工程大学学报,2015,37(4):69-73.

[17] 刘岑,吴元祥,刘兵,等.奥氏体不锈钢S30408抗拉强度分布规律研究[J].河北工业科技,2016,33(1):31-34.

[18] 刘岑,杨帆,吴元祥,等.钢材拉伸试验数据同质性的判别[J].武汉工程职业技术学院学报,2017,29(2):17-19.

[19] 刘小宁,李清,刘兵,等.厚壁圆筒爆破压力计算公式的工程适用性研究[J].现代制造工程,2016，(5):154-159.

ComparisonofTwoNormalRandomVariableDistributionParameters

Liu Xiaoning1Liu Bing1Yang Fan1Wu Yuanxiang1Liu Cen2Zhang Hong wei1

(1.School of Mechanical Engineering, Wuhan Vocational College of Softwareand Engineering, Wuhan 430205, Hubei;2.School of Mechanical and ElectricalEngineering, Hubei Light Industry Technology Institute, Wuhan 430070, Hubei)

In order to compare distribution parameter of two random variables, probability theory and mathematical statistics knowledge is applied to make a direct comparison. According to the tensile test data of austenitic stainless steel S30408 in different state, when the confidence level was 99% on both sides, distribution parameter size of the yield strength and tensile strength is compared respectively. When temperature drops from room temperature to liquid nitrogen temperature, the mean and standard deviation of the yield strength of prestrain austenitic stainless steel S30408 increase significantly at the same time. And its mean tensile strength increases significantly. At liquid nitrogen temperature, compared with non-prestrain, the yield strength mean of 9% prestrain austenitic stainless steel S30408 increases significantly, its mean tensile strength, standard deviation of yield strength and tensile strength show no significant changes.

distribution parameter; comparison; direct method; normal distribution; random variables

李文英)

2017-10-21

2017-11-23

湖北省教育厅科研项目(B2016545)；武汉市黄鹤英才(教育)计划

刘小宁(1963～)，男，二级教授，正高职高级工程师.E-mail：lxngjxy@163.com

TH142,O211.9,O212.1

A

1671-3524(2017)04-0001-05