考虑公交客流需求不确定性的发车间隔优化

詹 斌 鲁寒宇 杨雨婷 李日伟

(武汉理工大学交通学院 武汉 430063)

考虑公交客流需求不确定性的发车间隔优化

詹 斌 鲁寒宇 杨雨婷 李日伟

(武汉理工大学交通学院 武汉 430063)

以单条公交线路公交为研究对象，考虑乘客需求的不确定性，建立发车频率确定和非均匀发车间隔优化的双层模型，从系统的角度探讨公交车辆调度问题.下层模型中，以乘客候车时间成本和公交公司运营成本最少为目标函数，求得各时段最优发车频率.以下层模型为基础，上层模型以乘客候车时间最短为目标函数，利用遗传算法求解双层模型，求得各时段不均匀发车间隔，构建相应指标体系对方案进行评价.以广州市广286路公交为例，论证该方法可行性.结果表明，与均匀发车间隔调度方案相比，非均匀发车间隔调度方案能节约乘客候车时间和公交运营成本.

公交调度；需求不确定；非均匀发车间隔；双层模型；遗传算法

0 引 言

国内外学者对公交发车频率和发车间隔优化问题进行了深入研究.在发车频率确定方面，牛学勤等[1]考虑了满意度，提出了以乘客和企业加权满意度最大的确定性模型；姚宝珍等[2]考虑了乘客和运营企业双方利益，利用综合赋权法对双方进行权衡，并利用SCE-UA算法对模型进行求解；王佳等[3]考虑不同车型的影响，兼顾乘客和公交企业利益博弈，构建双层规划模型优化公交发车频率.在发车间隔优化方面，许旺土等[4]考虑公交系统中的随机事件和随机变量，构建社会福利最大化的随机期望值模型；Wu等[5-6]考虑公交车辆行驶时间的随机性，优化公交发车时刻表.

依据IC卡刷卡数据求得公交各站点刷卡上车人数，利用历史客流量数据估计当前周次客流量，考虑乘客需求不确定性，确定最优公交发车频率.在发车频率基础上，以乘客候车时间最少与公交运行成本最少为目标函数，建立随机客流需求下的鲁棒优化模型，利用遗传算法求解，生成最优公交发车时刻表.以广州广286公交线路为例，构建指标评价体系，评判非均匀发车方案与均匀发车方案的优劣性，验证方法和模型的可行性.

1 发车间隔优化的双层模型构建

1.1 模型构建的相关假设条件

对模型做如下假设：

1) 不考虑交通拥堵情况，假设公交以固定速度行驶，不考虑车辆行驶时间的不确定性.

2) 同一线路公交车型相同，严格按照时刻表发车，且1 d内公交运营始末时刻必发一班车.

3) 公交到站后，乘客能全部上车，没有乘客在站点滞留.

4) 不考虑公交车辆在各站点停留时间.

5) 假设乘客到达各站点服从均匀分布.

6) 公交运行固定成本包括燃油费、人工费、车辆折旧法及日常保养费等，假设公交每趟次营运成本为定值，某条公交线路车辆营运成本仅与发车频率有关.

7) 假设城市常住人口与流动人口数量之比和IC卡刷卡人数与投币人数数量之比相等.

1.2 确定发车频率的鲁棒优化模型

1.2.1确定性模型

综合考虑运营成本和候车时间的影响，以公交运行1 d乘客候车时间成本和公交车辆营运成本综合最少为目标函数，确定公交发车频率.

1) 乘客候车时间成本最少 以乘客最短候车时间为目标函数，建立目标函数为

(1)

式中：I为全天公交运行时段；J为公交线路站点；Cwait为公交运行1 d乘客候车时间成本；fare为乘客单位候车时间成本,元/(人·min)，按当地乘客每分钟平均收入确定数值；pij为i时段到达j站点的客流量,人，由上周同一天IC卡刷卡数据统计获得；Fi为i时段时长；fi为公交车辆发车频率(辆/小时)；Fi/fi为i时段内公交车辆发车间隔,min.

2) 公交车辆营运成本最少 以公交车辆运营成本最少为目标函数，建立目标函数为

(2)

式中：w为公交每趟次营运成本；Cope为公交车辆营运成本.

综上，确定性模型的总目标及约束为

(3)

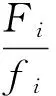
(4)

式中：Ccer为确定性模型下综合考虑乘客候车时间和公交营运成本的总成本；tmin，tmax为最小、最大发车间隔；α，β为权重系数，α+β=1，α，β具体取值由专家打分法确定.

1.2.2乘客需求不确定的鲁棒性模型

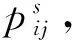
(5)

式中：f(s)为s的概率密度函数，所有可能事件的期望值为

(6)

模型考虑可能事件实际成本与期望成本的偏差，实际成本大于期望成本会对模型造成影响，反之，不会对模型有影响.故在模型中，要保证偏差尽可能小，建立以乘客总成本最小的鲁棒性模型.

(7)

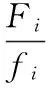
(8)

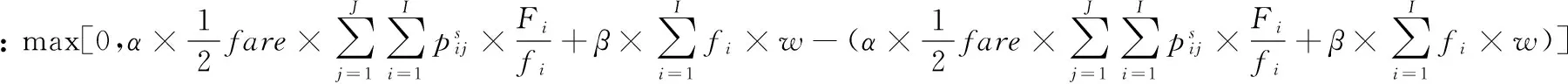
1.3 非均匀发车间隔优化模型

上下层模型以发车频率为纽带，发车频率已由下层模型求得，故公交车辆营运成本固定，只需考虑乘客候车时间最少.以最大、最小发车间隔为约束条件，建立如下数学模型：

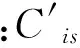
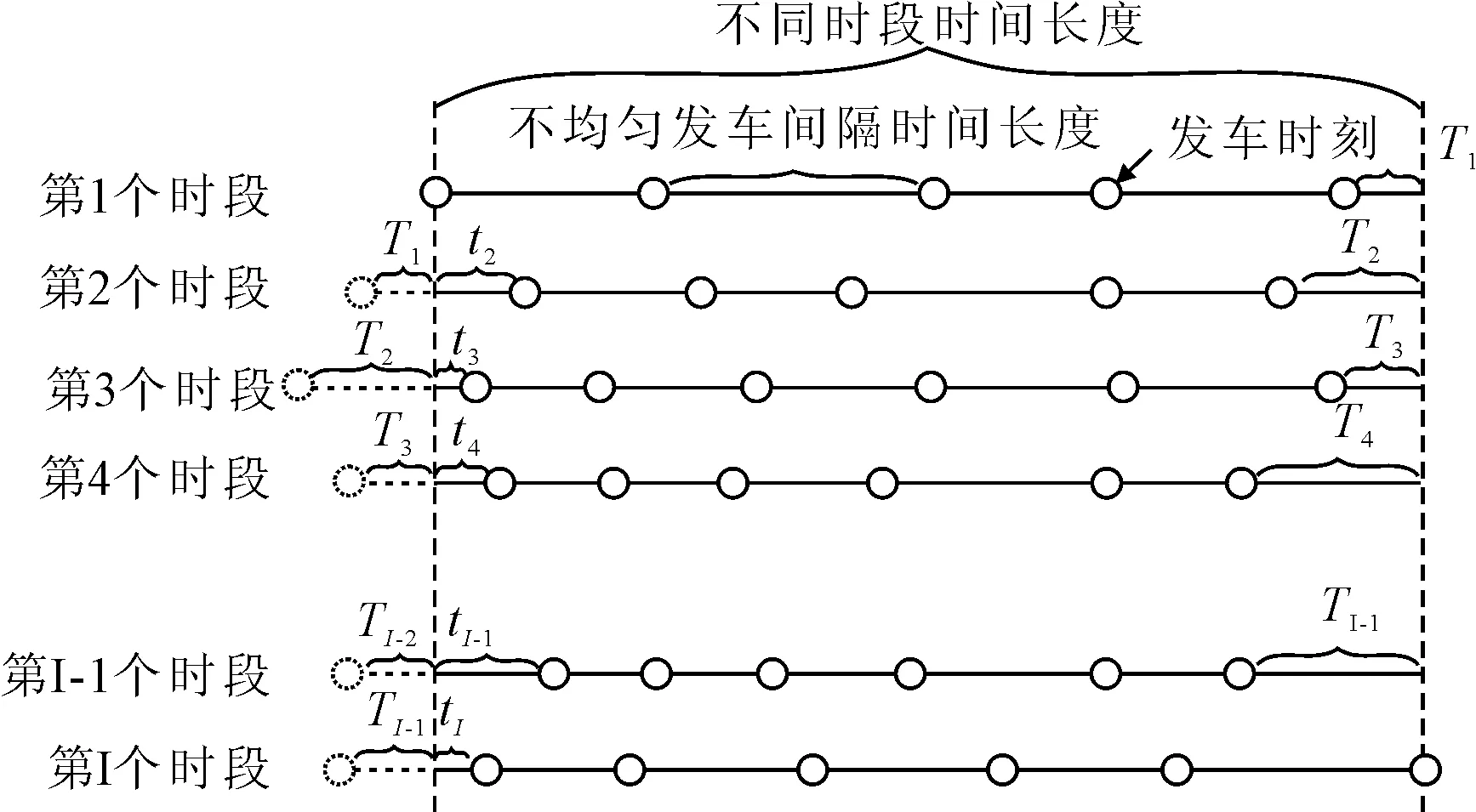
图1 各时段非均匀发车间隔

考虑乘客需求的不确定性，求得所有可能事件总成本的期望值为

f(s)ds

(10)

考虑目标函数中要保证可能事件实际成本与期望成本的偏差尽可能小，原模型可变为

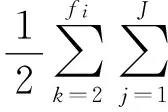
(11)

s.t.tmin≤tik≤tmax

(12)

tmin≤Ti+ti+1≤tmax

(13)

(14)

Ti≥0

(15)

ti≥0

(16)

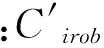
1.4 公交发车调度方案评价指标

建立公交调度评价指标体系，用于评价公交车辆不同发车间隔调度方案，见图2，各指标权重系数由德尔菲法确定.

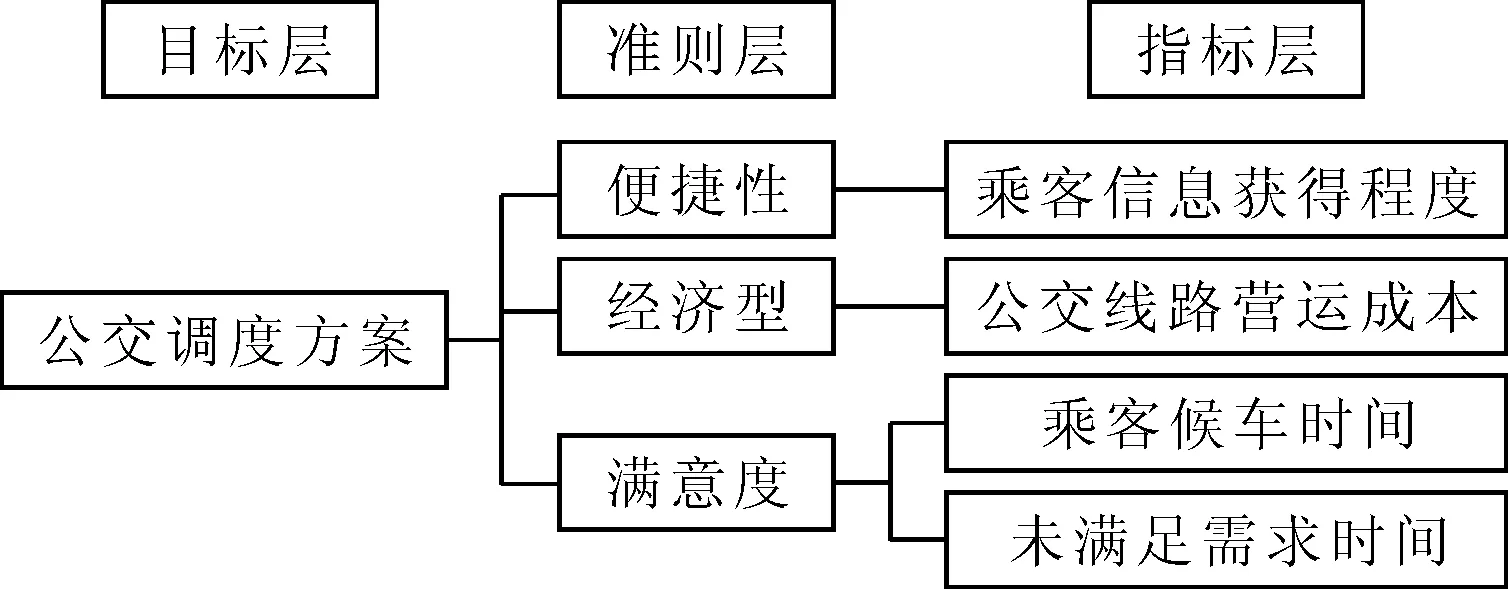
图2 公交调度评价指标

由于各指标间量纲不同，利用“奖优惩劣”的思想[7-8]，利用[0，1]线性变换对上述定量指标标准化处理，将三个包含单位的指标值转换为量纲一的量，数值越大表示指标越优.

1) 乘客信息获得程度量化值ϖ1，见表1.

表1 乘客信息获得程度量化标准

2) 公交日常营运成本量化值ϖ2公交日常营运成本与公交发车频率有关，即

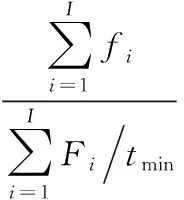
(17)

3) 乘客候车时间量化值ϖ3乘客候车时间与公交发车间隔有关，即

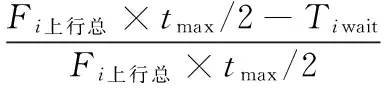
(18)

式中：Tiwait为i时段乘客总候车时间.

4) 未满足需求时间量化值ϖ4

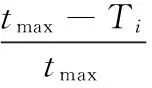
(19)

2 模型求解

2.1 下层模型求解

将全天划分为I个时段，在下层模型中，由假设6，每个时段发车频率相同，且均满足式(8).由于运算过程简单易操作，故利用EXCEL求解模型，求解步骤如下：

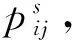
步骤2用EXCEL计算式(7)，在满足式(8)的条件下，求得i时段所有整数发车频率下最小目标函数值Ccer及最优公交车辆发车频率fi.

步骤3断是否求得所有时段最优发车间隔，若是，则结束运算，输出所有时段最优公交车辆发车频率fi；若否，令i=i+1，转到步骤2.

2.2 双层模型求解

下层模型已求得各时段最优发车次数fi，(ti，ti1，ti2，…tik，Ti)为实数编码，该编码中所有实数的和为i时段时间长度.利用遗传算法求得第一个时段最优不均匀发车间隔，然后利用式(13)和T1值筛选t2可能取值，利用相同方法求得第二个时段最优不均匀发车间隔，依此类推，可求得所有时段最优不均匀发车间隔.

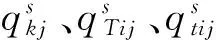
步骤2按照各时段发车间隔进行实数编码，编码为(ti，ti1，ti2，…tik，Ti).

步骤3令i=i+1，初始化种群.利用式(13)、(14)和Ti-1值筛选ti可能取值，采用随机取值方式取M个个体作为初始种群.

步骤4计算每个染色体适应度fitness，适应度函数表达式为

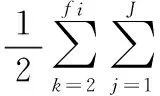
(20)

步骤5遗传算子.对染色体进行比例选择，概率为Pz，该值与适应度大小有关；对配对好的染色体进行单点交叉，概率为Pc；采用基本位变异，概率为Pm；代沟值为GGAP.

步骤6判断是否满足终止条件.令迭代次数为Dx次，Dx数值大小由站点数量决定.判断是否达到迭代次数，若满足，输出适应度最优染色体，转到步骤7；若不满足，返回步骤4.

步骤7判断是否i=I，若是，则结束运算；若否.则转到步骤3.

3 实例分析

3.1 公交IC卡刷卡数据处理

当前对公交客流数据收集处理分析技术比较成熟，戴霄等[9]统计分析了IC卡刷卡数据，利用数据进行上下车站点推算，将IC卡数据转化为公交规划、调度与运营管理的基础数据；Farzin[10]利用ADC数据、GPS数据和IC卡刷卡数据对乘客上车站点进行判断；徐文远等[11]结合公交系统GPS数据和IC卡刷卡数据的时刻匹配，提出乘客上车站点的判断方法.

以广州市广286路公交2015年1月4日上行刷卡数据为例(广卫路总站—黄岐第一城总站，06:30—22:00)，优化下周同一日即11日上行发车间隔，公交线路见图3.

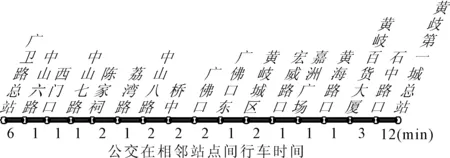
图3 广州市广286路公交运行线路及各站点用时

利用聚类分析法对IC卡刷卡数据进行分析，通过IC卡刷卡数据统计每个小时客流量，2015年广州市常住人口与流动人口比例为1∶1，由假设7，可得出广州市广286路公交客流量统计数据见图4.

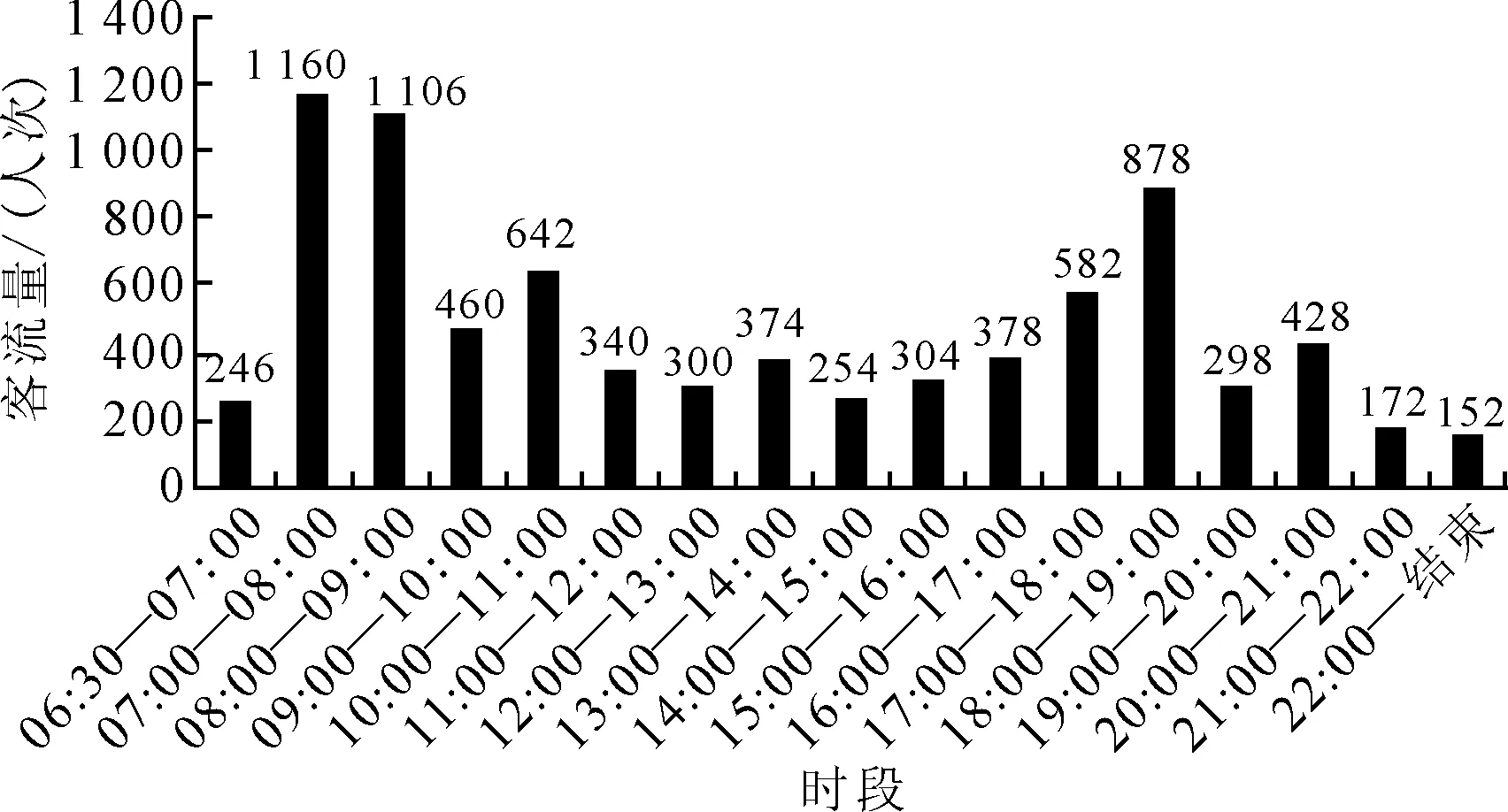
图4 广州市广286路公交各时段客流数据统计

统计每分钟客流量，各时段客流量在90%～110%的范围内以1%为单位变动，且客流量变动概率相等，本实例中存在21种可能变动情况，各种可能情况概率为1/21.

3.2 发车频率确定

将各时段客流量数据代入下层模型，模型参数设计见表2.

表2 下层模型参数设计

利用EXCEL求解式(8)，分别求解不同时段最优发车频率，第1，2，6，16时段不同发车间隔目标函数值计算结果见图5，全天各时段最优发车频次见图6.

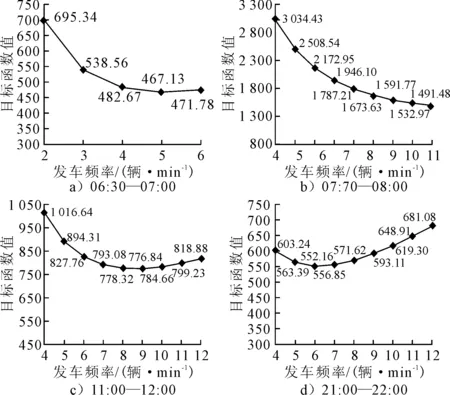
图5 第1，2，6，16时段不同发车间隔目标函数值

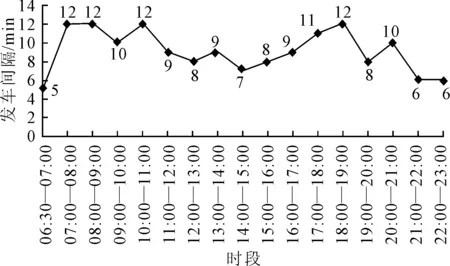
图6 各时段发车频率

3.3 非均匀发车间隔优化

下层模型已求得各时段最优发车频率，上层模型在其基础上求得各时段最优不均匀发车间隔.模型参数设计见表3.

以第1～2时段(06:30—08:00)为例，利用历史IC卡刷卡数据求出各时段每分钟上车刷卡人数，由此预测每分钟上车客流量，见表4.

表3 下层模型参数设计

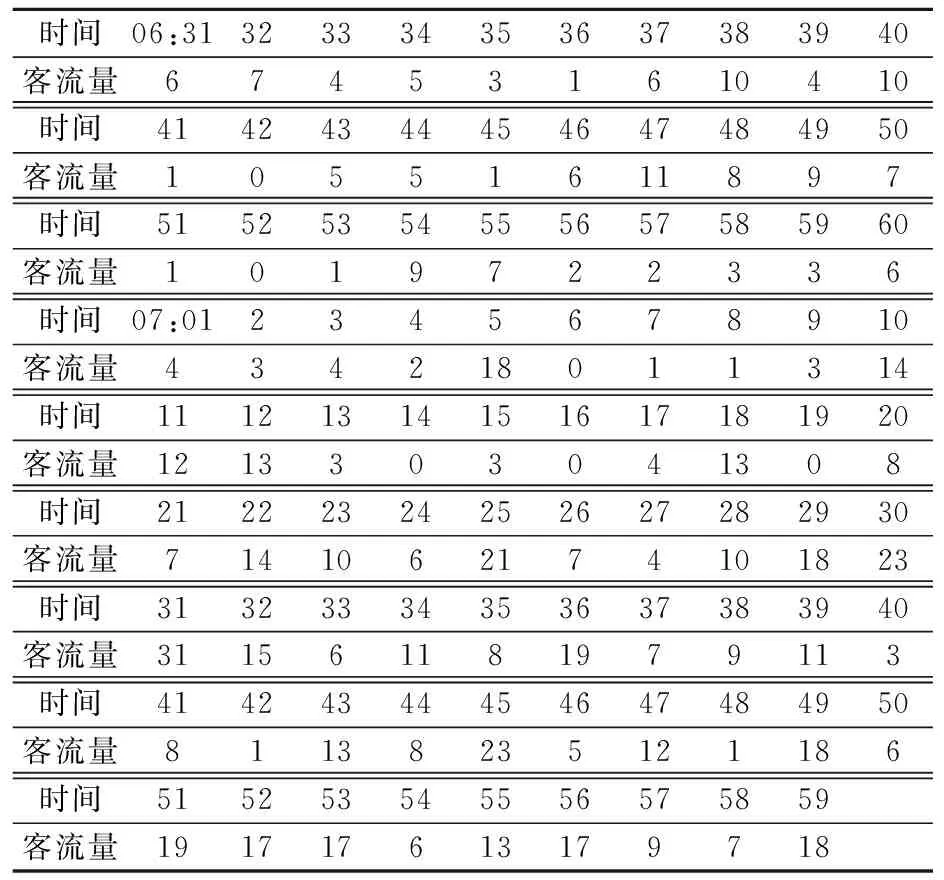
表4 第1～2时段每分钟客流量(06:30—08:00)

注：客流量单位为人/min.

利用Matlab 2014a对模型编程求解，可求出第一时段最优不均匀发车间隔数值为5，5，6，5，5，当前时段结尾发车间隔未覆盖时间区域为4分钟，该时段最小适应度函数值为2 172.9；利用相同方法，可求得第二时段发车间隔数值为1，5，5，5，5，5，5，5，5，5，5，5，当前时段结尾发车间隔未覆盖时间区域为4 min，以06:30—08:00为例，公交车辆发车时刻为06:30，06:35，06:40，06:46，06:51，06:56，07:01，07:06，07:11，07:16，07:21，07:26，07:31，07:36，07:41，07:46，07:51，07:56.同理可求得其他时段发车间隔和公交车辆发车时刻表，由于数据量较大，在此不一一罗列.

3.4 不同发车调度方案评价

考虑均匀发车和不均匀发车两种调度方案.由图6下层模型计算结果可知，第1，2时段(06:30—08:00)最优发车频率为17次，采用均匀发车调度方案，均匀发车间隔为5 min,07:50—08:00时刻内共10 min客流需求未满足，公交车辆均匀发车时刻为06:30，06:35，06:40，06:45，06:50，06:55，07:00，07:05，07:10，07:15，07:20，07:25，07:30，07:35，07:40，07:45，07:50.

分别对两种发车调度方案进行评价，利用式(17)～(20)计算不同调度方案各指标数值，结果见表5.

表5 不同公交调度方案指标值

利用各指标权重值与各指标量化值乘积的累和计算不同公交调度方案综合指标值，非均匀发车调度方案综合指标值为0.782 6，均匀发车调度综合指标值为0.721 4.所以，可判断非均匀发车调度方案优于均匀发车调度方案.

4 结 束 语

通过构建考虑乘客需求的不确定性的双层模型，优化公交非均匀发车间隔.利用广州市广286路公交进行验证，结果表明，非均匀发车调度方案在公交日常营运成本、乘客候车时间、未满足乘客需求时间等方面有较大优势，但是该方案信息获得程度较低.通过对不同评价指标赋予权重、综合评价，得出非均匀发车间隔调度方案优于均匀发车调度方案，文中提出的方法和模型能较好的解决非均匀发车间隔优化问题.

但是，从公交IC卡刷卡数据中仅可得到乘客上车信息，较难获取下车信息；假设乘客到达各站点服从均匀分布，但仍与实际情况有差异；未考虑车队规模的影响，也未考虑交通拥堵的影响和公交走行时间的随机性，因此模型应用具有一定的局限性.下一步将在模型中考虑车队规模的影响和公交走行时间的随机性，提高模型准确性.

[1] 牛学勤,陈茜,王炜.城市公交线路调度发车频率优化模型[J].交通运输工程学报，2003(4):68-72.

[2] 姚宝珍,杨成永,沈飞,等.基于综合集成赋权法的公交发车频率优化模型[J].交通运输系统工程与信息，2011(2):124-129.

[3] 王佳,胡列格,贺翔.城市公交发车频率优化的双层规划模型及算法[J].系统工程，2013(12):69-73.

[4] 许旺土,何世伟,宋瑞,等.多时段公交发车间隔优化的随机期望值模型[J].北京理工大学学报，2009(8):676-680.

[5] WU Y, TANG J, YU Y, et al. A stochastic optimization model for transit network timetable design to mitigate the randomness of traveling time by adding slack time[J]. Transportation Research Part C: Emerging Technologies，2015,52:15-31.

[6] CEDER A, GOLANY B, TAL O. Creating bus timetables with maximal synchronization[J]. Transportation Research Part A: Policy and Practice，2001,35(10):913-928.

[7] 张颂,陈学武,陈峥嵘.基于公交IC卡数据的公交站点OD矩阵推导方法[J].武汉理工大学学报(交通科学与工程版)，2014,38(2):333-337.

[8] 卢蝶,靳文舟.基于累积前景理论的公交调度优化灰关联评价方法[J].武汉理工大学学报(交通科学与工程版)，2013,37(3):608-611.

[9] 戴霄,陈学武.单条公交线路的IC卡数据分析处理方法[J].城市交通，2005(4):77-80.

[11] 徐文远,邓春瑶,刘宝义.基于公交IC卡数据的公交客流统计方法[J].中国公路学报,2013(5):158-163.

Optimization of Departure Intervals Considering Uncertainty of Bus Passenger Flow Demand

ZHANBinLUHanyuYANGYutingLIRiwei

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)

Taking a single bus line as the research object, the bi-level programming model was established to determine the frequency of the hair car and the non-uniform interval optimization considering the uncertainty of passenger demand, and the problem of bus vehicle scheduling was analyzed from the perspective of the system. In the lower model, the target functions were the minimum cost of passenger waiting time and the operating cost of the bus company. The optimal departure frequency under different intervals could be sloved in this model. Based on the lower level model, the upper model took the shortest waiting time of passengers as the objective function. Using genetic algorithm to solve the bi-model programming the non-uniform departure intervals of different periods were figured out and the corresponding index system was constructed to evaluate different schemes. Finally, this method was verified by the example of GuangZhou guang-286 bus. The results show that the non-uniform departure interval could save passenger’s waiting time and Bus operating costs, compared with the uniform departure interval scheduling scheme.

bus scheduling; demand uncertainty; non-uniform departure interval; bi-level programming model; genetic algorithm

U492.22

10.3963/j.issn.2095-3844.2017.06.018

2017-09-27

詹斌(1966—)：男，博士，教授，硕士生导师，主要研究领域为交通运输规划与管理