电流模式的高阶曲率补偿CMOS带隙基准源

张普杰，王卫东，李耀臻

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

电流模式的高阶曲率补偿CMOS带隙基准源

张普杰1，王卫东2，李耀臻3

(桂林电子科技大学 信息与通信学院，广西 桂林541004)

因为传统的带隙电压基准源只经过了一阶温度补偿，且输出电压只能在1.2V左右，所以为了得到一个可调的、更高精度的电压基准源，提出了电流模式的带隙电压基准源电路。电路采用了高阶曲率补偿方法，且输出的基准电压可根据输出电阻的大小进行调节。电路采用gpdk090CMOS工艺，通过Spectre仿真，当电源电压为3.6V、在-60℃～-120℃温度范围内、温度系数为14.4×10-6/℃ 时电源电压抑制比为78.3dB，输出电压平均为1.162V。

带隙电压基准源；高阶曲率补偿；温度系数；电压抑制比

0 引言

基准源是模拟集成电路设计中经常用到的重要电路，分为电压和电流基准源。因为基准源与电源电压、工艺模型、环境温度基本无关，并且基准源有高的电源抑制比和低的温度系数，所以可以为电路提供稳定的电压或电流，在A/D或D/A转换模块、LDO(低压差线性稳压器)、SOC(系统集成芯片)等系统中扮演着非常重要的角色。

传统的带隙基准源是把具有负温度系数的电压(VBE)与具有正温度系数的电压(ΔVBE)分别加以不同的权重然后相加，使两者相抵消，从而获得与温度无关的电压。但传统的带隙电压基准源也有一个缺点，当具有不同温度系数的电压相抵消时，会得到一个1.2 V左右的电压，这时如果电源提供的电压接近1.2 V时该带隙基准源就不适用了。为了能获得输出可控的基准电路，本文基于电流模式电路提出一种具有高阶温度补偿的、输出电压可调的带隙基准电压源电路。

1 传统的带隙电压基准源结构

正如上文提到的，典型的带隙电压基准源电路是把具有负温度系数的电压(VBE)与具有正温度系数的电压(ΔVBE)分别加以不同的权重然后相加，使两者相抵消，从而获得与温度无关的电压(理论上在某一确定温度下的温度系数为0，一般为300 K)：

VREF=αVBE+β(ΔVBE)

(1)

这里ΔVBE(也可写为VTlnn)是分别工作在两个电流密度下的两个晶体管的基级-发射极电压的差值，VBE为晶体管的基级-发射极电压，α、β为分别对正负温度系数加的权重。在室温下∂VBE/∂VT≈-1.5 mV/°K，∂VT/∂T≈+0.087 mV/°K(VT=kT/q，k为波耳兹曼常数)。把式(1)对温度微分，调节α、β的值可以使VREF的温度系数在T=300 K时为0[1]。

图1为传统的带隙电压基准源电路[2]，M1、M2、M3、M4构成环路，所以流经Q1、Q2的电流相等。M1～M4、Q1、Q2和R1构成PTAT(与绝对温度成正比)电路，Q2和Q3与Q1发射结面积之比为N，假设电路中MOS的宽长比相同。如果流过M1的电流为I，则M2、M5的电流也为I，VGS3=VGS4,从而VX=VY。所以有：

VEB1=VEB2+IR1

(2)

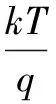
(3)

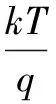
(4)

IS2=NIS1

(5)

由式(2)～式(5)可推得：

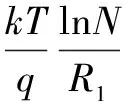
(6)

所以

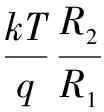
(7)

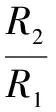
VREF≈VBE3+17.2VT≈1.25 V

(8)

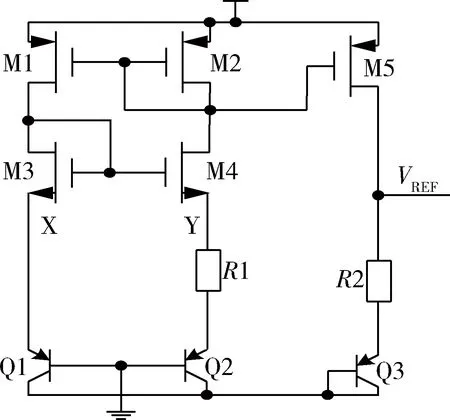
图1 传统的带隙基准源结构

由以上推导可以看出常用的带隙基准有以下缺点：只是对电路进行了1阶的温度补偿；虽然输出基准电压会随着温度有小幅度的变化，但基本上在1.2 V左右，当电源电压接近1.2 V时该电压源就不适用了。为了能得到输出可控、精度更高的带隙基准源，本文基于电流模式电路提出一种具有高阶曲率补偿的、输出电压可调的电路结构。

2 带隙电压基准源的高阶曲率补偿

相比于典型的电压基准源只进行了一阶的温度补偿，本文提出的电路还加入了高阶曲率补偿电路。针对本文采用的电流模式的高阶曲率补偿方法，可用两个BJT的电压差ΔVBE产生的电流来补偿。

2.1 三极管的基极-发射极电压的温度系数

从文献[3]中可得到晶体管的基极-发射极电压为：

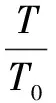
(9)

上式中，VBE(T)表示晶体管的基极-发射极电压随温度改变时的值；Vg(T)表示硅的带隙电压值，该值由材料本身决定；α与具体采用的工艺有关，表示载流子迁移率与温度的关系；β表示集电极电流与温度的相关性，当IC与温度相关时β=1，与温度无关时β=0；式(9)中包括常数项、一阶项、高阶项，典型的带隙基准源只是对其中的一阶项进行了处理，而高阶项没有得到补偿，为了减小高阶项对基准源的干扰，提出了一种基于电流模式的高阶曲率补偿电路。

2.2 高阶曲率补偿带隙基准源具体电路

总电路由启动电路、IPTAT电路、电流相加电路和ICTAT(与绝对温度成反比)电路、INL(两个晶体管的基极-发射极电压差ΔVBE产生的电流)模块组成[4]。图1中MOS器件的沟道长度调制会导致显著的电源依赖性。为了避免这个问题，图1的MOS管全用共源共栅电路代替，为了避免外加偏置的设计，文中采用了自偏置的共源共栅的结构，图2中R1、R2、R5、R6提供合适的偏置，使所有的MOS管都工作在饱和区。电路中两个共源共栅电路分别产生IPTAT和ICTAT，并且用两个晶体管的基极-发射极电压差ΔVBE产生的电流INL来进行微调，用电流相加模块把三部分电流进行相加，最后根据Vref=Rref×Iref得到一个与Rref成比例的电压。

IPTAT模块由M1～M8、R1、R2、R3、Q1、Q2组成(Q1的发射结面积为Q2的N倍),由此可推得IPTAT为：

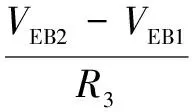
(10)

INL模块由M9、M10、R4、Q3构成，由图中可得INL为：

(11)

由于VEB2与IPTAT有关，由式(9)可得：

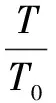
(12)

由于VEB3与ICTAT无关，可得：

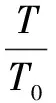
(13)

把式(12)、(13)带入式(11)可得：

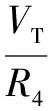
(14)

ICTAT模块由M15～M22、R5、R6、Q4、R7组成(Q1的发射结面积为Q4的N倍),由此可推得ICTAT为：

(15)

以上推得的IPTAT、ICTAT、INL电流经过相加模块可得输出电流Iref为：

Iref=IPTAT+ICTAT+INL

(16)

把式(10)、(14)、(15)带入式(16)可得：

(17)

由上式可以看出此时推得的Iref中包括一阶温度项(式中大括号)、高阶温度项(式中的对数项)以及硅的带隙电压(其中包括一阶项和高阶项)。为了得到与温度无关的电流，首先要对一阶温度项进行补偿，可以调节R3、R7、N的值，使式中的一阶项为0。接下来对式中的高阶项进行补偿，消除式中的对数项。可以发现电阻R7既与一阶项有关也与高阶项有关，所以一阶项的消除和高阶项的消除是相互制约的，在调制电路时要多次尝试，以得到最优化的电路。

根据公式Vref=Iref×Rref，调节Rref的大小就能得到需要的电压值。

图2 整体结构

2.3 启动电路

因为电路启动时带隙中电流可能为零，这时带隙会一直处在关断状态，也就是“简并”点的问题[1]。为了避免“简并”点的问题，本文引入启动电路结构，如图2中S1、S2、S3、R、Q5所示。当电路上电时S1、S2接通并通过S2的漏极给S3的栅极充电，使S3的栅极电位提高，从而使M5、M6、M19、M20导通，各支路都有电流流过，最终达到平衡点。这时S3会导通，从而把S2关断，S1与S3导通，电流流向Q5，后面的电路工作正常后，启动电路就不会再起作用[2]。

3 仿真验证

采用Cadence公司的Spectre软件对整体电路结构进行仿真，采用gpdk090 CMOS 工艺。电源电压为3.6 V，仿真温度在-60℃～120℃范围变化。仿真结果如图3、图4所示。

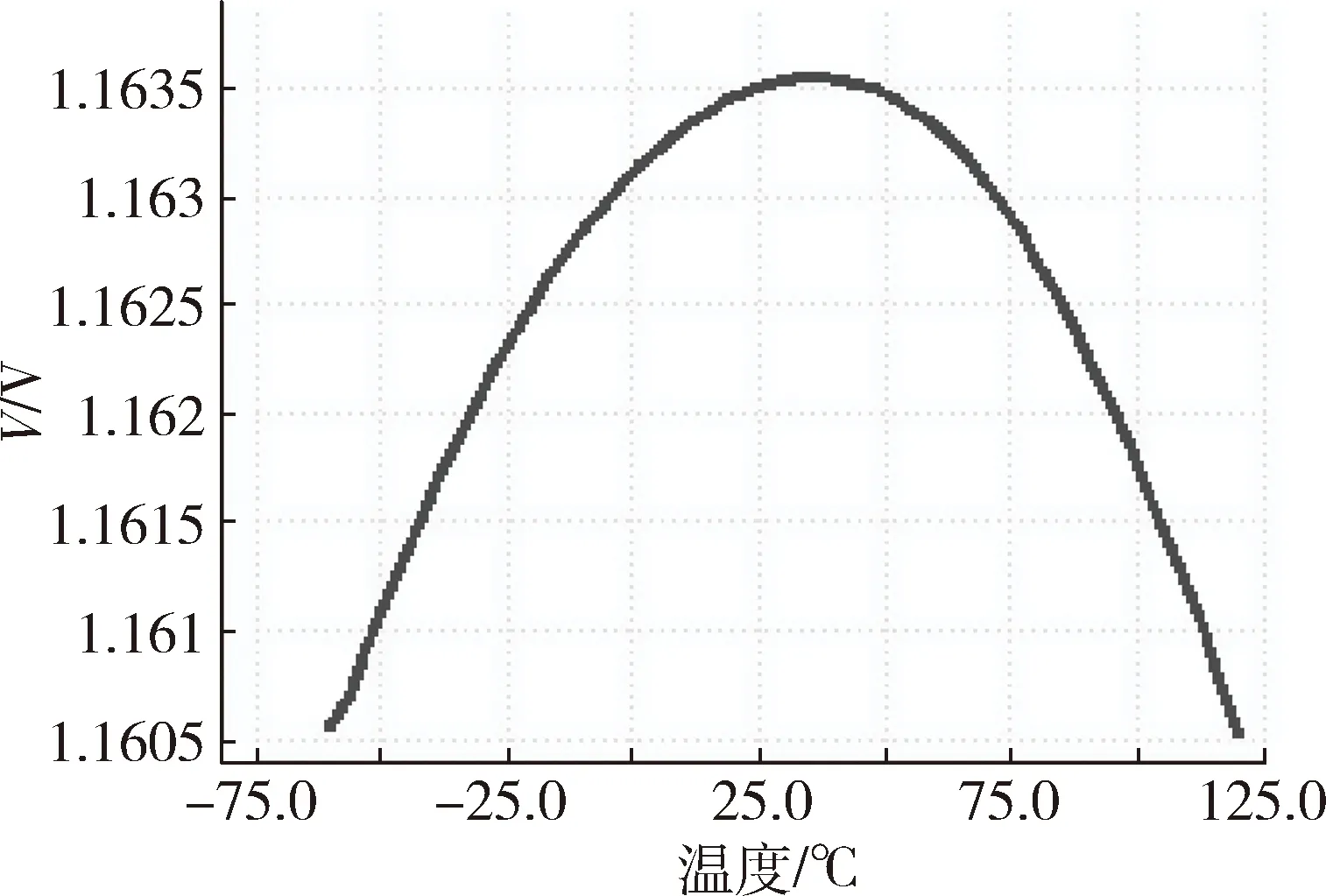
图3 电压随温度变化的曲线

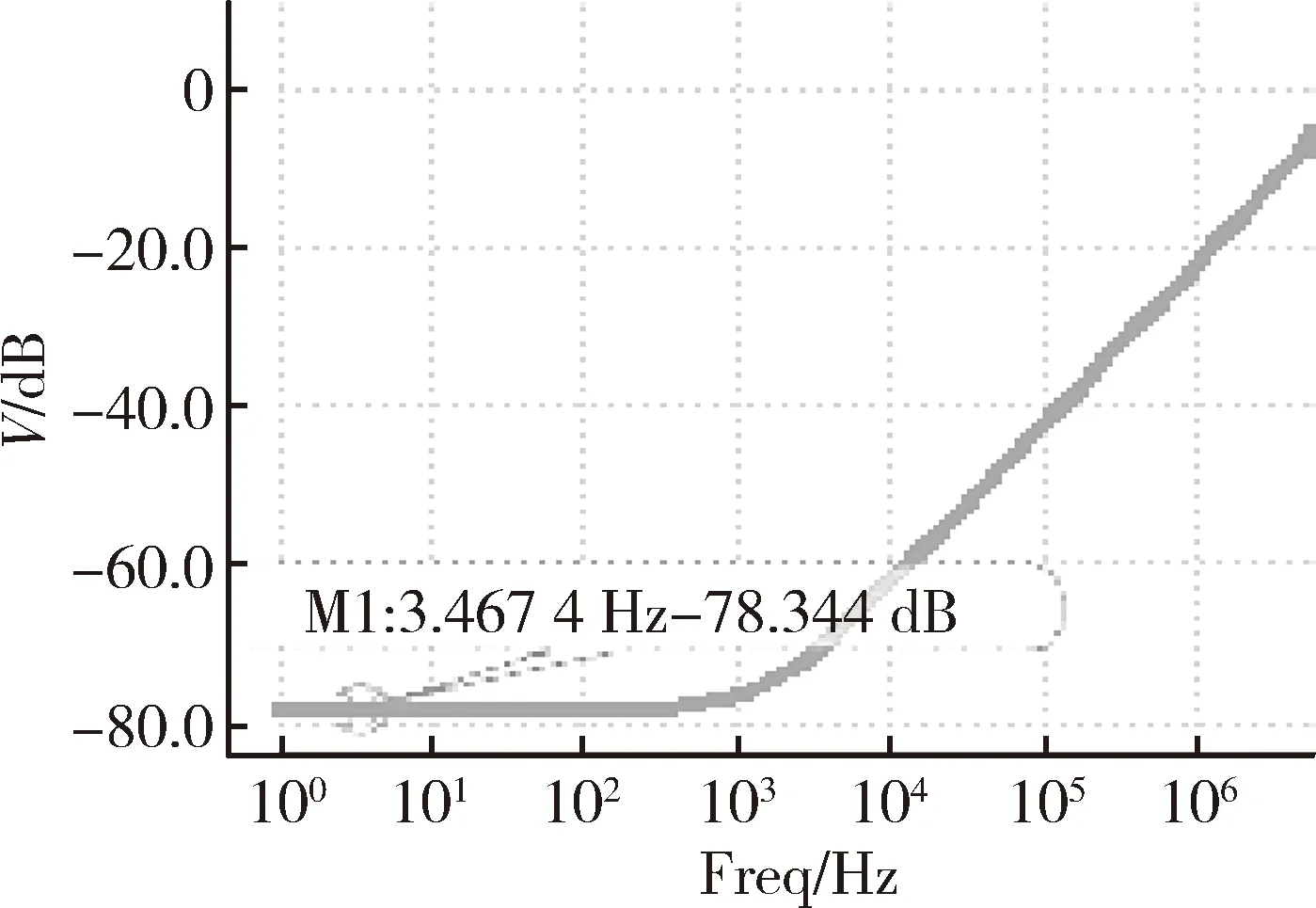
图4 电源电压抑制比

图3 是对输出电压温度特性的仿真，当温度在-60℃～120℃范围时，输出电压基本在1.162 V，温度系数大约为1.44×10-5/℃。图4是对电源抑制比的仿真，电源提供的电压为3.6 V，温度为27℃时，可以得到，该结构有较高的电源抑制比，频率较低时为-78.3 dB。

表1中列出了本文带隙基准源的部分参数，并与其他文献中的带隙基准源进行了对比，从表中得出，相比于其他文献中的参数，本文的电路有较好的电源抑制比和温度系数。

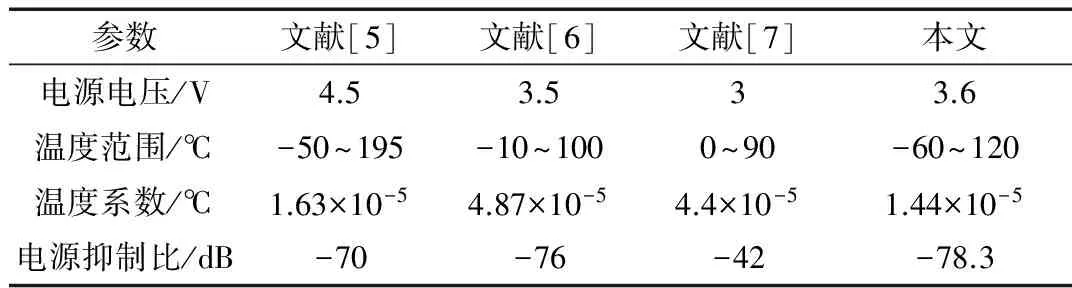
表1 与其他文献中的带隙基准源比较

4 结论

文中设计了一种电流模式的带隙电压基准源电路结构，通过把3个温度系数不相同的电流相加得到与温度关系很小的电压。为了使电路有更好的性能，电路采用了高阶曲率补偿方法。从仿真结果可以看出，当电源提供的电压为3.6 V，温度在-60～120℃范围时，温度系数为1.44×10-5/℃，电源抑制比为-78.3 dB。相比于其他文献中的带隙电压基准源有更好的性能。

[1] RAZAVI B.模拟CMOS集成电路设计[M].陈贵灿,译.西安:西安交通大学出版社,2003.

[2] 周永峰,戴庆元,林刚磊,等. 一种用于CMOS A/D转换器的带隙基准电压源[J]. 微电子学,2009,39(1):25-28,33.

[3] 李斌桥,许延华,徐江涛,等. 高阶曲率补偿电流模式的CMOS带隙基准源[J]. 天津大学学报(自然科学与工程技术版),2008,41(12):1459-1464.

[4] 胡勇,彭晓宏,刘云康,等. 一种新型电流模式带隙基准源的设计[J]. 微电子学,2013,43(4):457-459，463.

[5] 梁爱梅,凌朝东. 电流镜型二次曲率补偿的带隙基准源设计[J]. 华侨大学学报(自然科学版),2010,31(3):267-271.

[6] Zhao Chenyuan,Huang Junkai. A new high performance bandgap reference[C]. 2011 International Conference on Electronics,Communications,and Control(ICECC),2011:64-66.

[7] 陈友福,李平,刘银,等. 一种新型的BiCMOS带隙基准电压源[J]. 微电子学,2006,36(3):381-384.

High-order curvature-compensated CMOS of current mode

Zhang Pujie1,Wang Weidong2,Li Yaozhen3

(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

The traditional bandgap voltage reference source is only the first-order temperature compensated ,and the output voltage reference is only at about 1.2 V. in order to get an adjustable and higher precision voltage reference,a current-mode bandgap voltage reference source was presented in this paper. Circuit adopted high-order curvature compensation methods,and the output of the reference voltage can be adjusted according to the size of the output resistance.It was fabricated in gpdk090 CMOS process.By simulation with Spectre,supplying voltage of 3.6 V,a temperature coefficient of 14.4×10-6/℃ in the temperature range of -60℃ to 120℃,the power supply rejection ratio is 78.3 dB,and the averaged reference voltage is 1.162 V.

bandgap voltage reference; high-order curvature compensation; temperature coefficient; PSRR

TN432

A

10.19358/j.issn.1674-7720.2017.24.005

张普杰，王卫东，李耀臻.电流模式的高阶曲率补偿CMOS带隙基准源J.微型机与应用，2017,36(24)：16-18，21.

2017-06-24)

张普杰(1991-)男，硕士研究生，主要研究方向：模拟集成电路设计。

王卫东(1956-)男，教授，硕士生导师，主要研究方向:模拟集成电路与电流模式电路。

李耀臻(1989-)，男，硕士研究生，主要研究方向：模拟集成电路设计。