基于Schur补性质的时变采样系统控制器设计

赵达

（黑龙江八一农垦大学理学院，大庆 163319）

基于Schur补性质的时变采样系统控制器设计

赵达

（黑龙江八一农垦大学理学院，大庆 163319）

针对一类具有多个采样周期的时变采样控制系统的控制问题，利用Schur补性质将控制器的设计问题转化为线性矩阵不等式问题，通过求解线性矩阵不等式设计出保持系统一致稳定的控制器，解决了在多个采样周期下系统的稳定性问题，小车和倒立摆模型的仿真结果验证了控制器设计方法的有效性。

时变采样；Schur补；线性矩阵不等式；控制系统

在采样控制系统中，通常都假定控制器按一个固定的周期采样。但是计算机负载的变化、网络的影响、设备的老化以及一些偶发的事故都可能导致采样周期发生波动，使采样控制系统时变，从而影响系统运行的性能，甚至影响系统的稳定性。在这种情况下，如何设计控制器使系统更稳定是一个非常实际的问题，受到研究者广泛关注[1-11]。讨论一类连续时间线性时不变系统，系统的被动时变采样周期在一个分布已知的有限个值之间切换，给出系统的控制器设计及仿真实例。

1 问题的提出

考虑如下的线性时不变系统

x˙（t）=Ax（t）+Bu（t）

y=Cx（t）+Du（t） （1）

其中 x（t），u（t）和 y（t）分别是具有适当维数的状态向量、控制输入向量和量测输出向量，A，B，C和D分别是具有适当维数的常数矩阵。

假设系统（1）的理想采样周期是T，离散化后的状态方程为

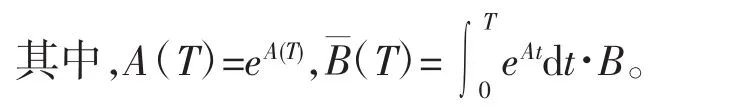
由于计算机负载的变化、网络的影响、设备的老化等因素，可能导致采样器的采样周期发生波动。不妨设采样周期在有限集{T1，T2，…，Tm}上取值，对应系统（1）的离散系统有m个，状态方程可以写成

如果此时按理想采样周期的状态方程设计控制器，则不能保证闭环系统稳定。下面设计状态反馈控制器

使得采样周期在有限集{T1，T2，…，Tm}上任意取值时，由（2）和（3）构成的闭环时变采样控制系统一致稳定。

（1）S＜0；

（2）S11＜0，S22-S12TS11-1S12＜0；

（3）S22＜0，S11-S12S22-1S12T＜0。

2 控制器设计

根据以上问题的描述以及离散时间线性时不变系统的稳定性理论，闭环系统（2）一致稳定的充分条件可以得到。

定理1如果存在对称矩阵P＞0和矩阵K，使得下面的矩阵不等式

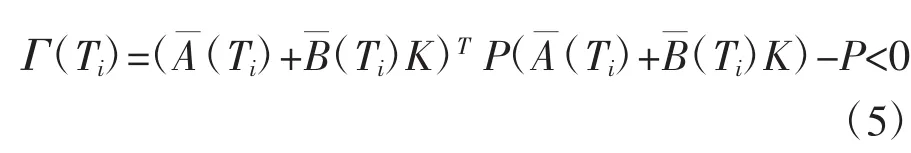
对所有的 i∈{1，2，…m}成立，则闭环系统（4）一致稳定。

证明：考虑Lyapunov函数

V（tk）=x（tk）TPx（tk）

对于闭环系统（4）以及任意的 i=1，2，…，m 有

如果 Γ（τ）＜0，那么

其中，β=inf{λmin（-Γ（Ti）），i=1，2，…，m}。因此，闭环系统（4）一致稳定。

定理1 给出了状态反馈控制器存在的充分条件，但是，所给矩阵不等式并不是线性的，实际当中实现控制器设计很难，进一步的定理如下。

定理2 如果存在对称矩阵p＞0和矩阵Q，使得下面的矩阵不等式

对所有的 i∈{1，2，…m）成立，则闭环系统（4）一致稳定。

证明：根据Schur补性质，（5）式可以转化成

将其左右同乘 diag（I，P）得

令Q=KP得

又由于以上各步均可逆，所以定理得证。

由定理2，状态反馈控制增益矩阵为

K=QP-1。

3 仿真实例

如图1，考虑小车和倒立摆问题。假定小车质量m1=0.6 kg，倒立摆质量 m2=0.3 kg，摆长 L=1 m，地面光滑。系统的状态变量选为，线性时不变连续系统的状态方程为

图1 小车和倒立摆Fig.1 A cart and inverted pendulum

假定系统的采样周期有三个可能取值T1=0.1 s，T2=0.12 s，T3=0.08 s，对应的采样控制系统是在三个采样周期下的三个离散系统间切换，所以采样控制系统是时变采样控制跳跃系统。

为仿真，假定在实际的控制系统中，Tk+1和最近的一次Tk有关，将Tk看作一个Markov链，设状态转移概率为

对应的状态转移矩阵为

在上述采样周期下，根据定理2，应用Matlab软件的LMI工具箱求解可得闭环系统的控制器增益为

K=[1.126 5 3.198 7 -41.680 0 15.819 1]

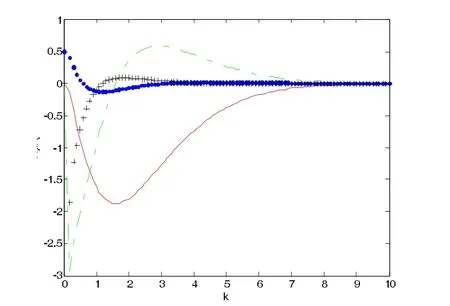
图2 小车和倒立摆模型的状态响应曲线Fig.2 State response curve of a cart and inverted pendulum

4 结论

应用线性矩阵不等式方法处理控制问题是目前控制领域中的一个热点问题，而利用Schur补转化为凸优化问题或线性矩阵不等式是线性矩阵不等式方法的重要内容。针对一类具有多个采样周期的时变采样控制系统的控制问题，利用Schur补性质将控制器的设计问题转化为线性矩阵不等式问题，通过求解线性矩阵不等式设计出保持系统一致稳定的控制器，解决了在多个采样周期下系统的稳定性问题，小车和倒立摆模型的仿真结果验证了控制器设计方法的有效性。

［1］ Zhang L Q，Shi Y，Chen T W，et al.A New Method for Stabilization of Networked Control Systems with Random Delays［J］.2005 American Control Conference，2005（6）：633-637.

［2］ Hu B，Michel A N.Stability analysis of digital feedback control systems with time-varying sampling periods［J］.Automatica，2000，36：897-905.

［3］ Katayama H，Ichikawa A.Receding horizon H∞ control for time-varying sampled-data systems ［C］//Proceedings of the 44th IEEE Conference on Decision and Control，and the European Control Conference，2005：951-956.

［4］ Mancilla-Aguilar J L，Garcia R A.On the exponential stability of nonlinear sampled-data systems with timevarying sampling periods［C］//Proceedings of the American Control Conference，2002：1290-1295.

［5］ Yu H W，Zheng Y F，Wang Z M.Stabilization of a Class of Nonlinear Sampled-data Control Systems［C］//Proceeding of the 6th World Congress on Intelligent Control and Automation，2006：853-857.

［6］ Hu L S，Bai T，Shi P，et al.Sampled-data control of networked linear control systems［J］.Automatica，2007，43：903-911.

［7］ Wang Y L，Yang G H.Yang，H∞ control of networked control systems with time-varying sampling period ［J］.Information and Control，2007，36（3）：278-284.

［8］ Wang Y L，Yang G H.H∞ controller design for networked control systems with packet dropout and time-varying sampling period［C］//Proceeding of the American Control Conference，2008：4973-4978.

［9］ Wang Yulong，Han Qinglong.Quantitative analysis and synthesis for networked control systems with non-uniformly distributed packet dropouts and interval time-varying sampling periods［J］.International Journal of Robust and Nonlinear Control，2015，25：282-300.

［10］ Wang Yulong，Han Qinglong.Modelling and controller design for discrete-time networked control systems with limited channels and data drift［J］.Information Sciences，2014，269：332-348.

［11］ Wang Yulong，Xiong Jie.Fault detection filter design for networked control systems with time-varying sampling periods and packet dropouts［J］.International Journal of Adaptive Control and Signal Processing，2016，30：790-806.

Controller Design for a Class of Time-varying Sampling System Based on Schur Complement

Zhao Da
（College of Science，Heilongjiang Bayi Agricultural University，Daqing 163319）

The control question with regard to a class of time-varying sampling control systems was presented，the controller design ensuring the uniform stability of systems with multi-sampling periods was transformed into resolving linear matrix inequality by Schur complement，and the simulation results by cart and inverted pendulum verified the effectiveness of the proposed controller design.

time-varying sampling；Schur complement；linear matrix inequality；control system

O151.21

A

1002-2090（2017）06-0060-03

10.3969/j.issn.1002-2090.2017.06.014

2017-02-20

赵达（1978-），男，副教授，黑龙江大学毕业，现主要从事物理教学与科研方面的工作。