四步相移法的非线性相位误差补偿方法*
赵贤凌, 刘建生, 张华煜, 武迎春
(1. 太原科技大学 材料科学与工程学院, 山西 太原 030024; 2. 太原科技大学 电子信息工程学院, 山西 太原 030024)
四步相移法的非线性相位误差补偿方法*
赵贤凌1,2, 刘建生1, 张华煜1, 武迎春2
(1. 太原科技大学 材料科学与工程学院, 山西 太原 030024; 2. 太原科技大学 电子信息工程学院, 山西 太原 030024)
在相位测量轮廓术中, 测量系统的gamma非线性是相位误差的主要来源. 系统gamma非线性使变形光栅条纹图像中出现高次谐波, 从而引起展开相位存在周期性误差. 对于四步相移法, 三次谐波是引起周期性误差的主要因素. 通过建立四步相移法的相位误差和主相位的关系模型, 在系统gamma值未知的情况下, 对非线性相位误差进行了补偿. 计算机仿真表明, 当系统的gamma值为2.2时, 使用本方法补偿前后的相位误差波动幅值分别小于0.006 3 rad和0.000 354 rad; 实验证明, 一个平面白板展开相位的均方根(RMS)在误差补偿后从0.035 rad降低到0.007 rad, 相位误差的最大值从0.086 7 rad减小到0.030 8 rad.
误差补偿; 四步相移法; gamma非线性; 三次谐波; 谐波系数
相位测量轮廓术(Phase Measuring Pro-filometry, PMP) 是一种测量精度高、 测量速度快和测量范围广的非接触测量方法, 被广泛应用在工业检测、 逆向工程和人体测量等领域[1-3]. 它通过采集多帧有一定相移且受物体表面调制的结构光条纹图像获取相位信息[4-6], 并根据投影仪和摄像机的内外标定矩阵获取被测物体表面的三维信息[7-8]. 在实际测量中, 变形光栅条纹图像会受到投影仪和摄像机的gamma非线性影响而呈现非正弦性, 因此硬件的gamma非线性成为相位测量轮廓术中相位误差的一个主要来源[9-10], 如何消除非线性误差便成为相位测量轮廓术研究的一个热点. 为了克服由gamma非线性引起的相位误差, 许伟等[11]采用二次多项式最小二乘拟合法近似输出条纹光强分布, 实现了包裹相位波动误差的补偿, 减小了投影仪非线性导致的系统测量误差; 周平等[12-13]建立了环境光和相位误差之间关系的模型, 使相位误差明显减小, 但是该方法需要投射全白和全黑图案到均匀平面白板上以确定变形条纹图像的平均灰度和调制度, 在一些工业生产现场, 此种方法是不实用的; Lei等[14]提出了用多频反相位误差法补偿相位的非线性误差, 投影仪将两套初相位相差π/4的相移光栅条纹图像投射到物体表面, 将两套光栅条纹图像的包裹相位取平均值, 可以达到抑制gamma非线性误差的目的, 但是此方法需要投射两倍数量的光栅条纹图像, 因此测量效率较低.
1 四步相移法的相位误差补偿方法
投影仪与相机的gamma非线性效应可被整体视为系统的γ值, 投射到被测物体表面的正弦条纹图像被物体表面调制后, 若摄像机采集到的变形光栅图像没有发生饱和, 则变形光栅条纹图像中某像素点的光强值可以表示为[10]

式中:γ为系统的gamma非线性值;α为常数;φ为畸变光栅的相位主值;Mn和Nn分别为第n幅变形光栅条纹图像的平均强度和调制度,δn=2π(n-1)/4,n=1,2,3,4.
对于四步相移法, 假设4幅图像的平均强度和调制度相等, 则式(1)可以简记为
再将式(2)变换为
将式(3)按照广义二项式定理展开为
根据余弦降幂公式, 式(4)可以改写为
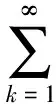
式中:B0为变形光栅条纹图像的直流分量系数,Bk(k是整数)为k次谐波的系数. 当γ是整数, 且k>γ时,Bk=0; 当γ是非整数时,Bk是一个无限序列之和且收敛,Bk可表示为
由式(6)和式(7)可知, 要求得Bk就必须先求系统的gamma值. 一般情况下, 系统的gamma值并不是一个整数, 因此变形光栅条纹图像中存在高次谐波(Bk≠0)导致相位误差的存在. 在实际光栅图像中, 很少发现由高于三次谐波的高频谐波引起的相位误差[15], 并且Bk会随着k值的增大而迅速减小[12], 因此本文考虑的最高谐波为三次谐波. 将δn=2π(n-1)/4代入式(5)得到In(n=1,2,3,4)的表达式为
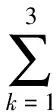
采用四步相移法得到的相位主值φ′为
式中:φ为理想的相位主值,
相位误差Δφ=φ-φ′, 由式(8)~(10)可得
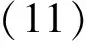
利用正切函数的差公式, 并将式(8)和式(9)代入式(11)可得
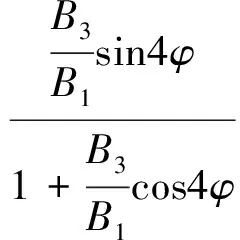
(12)
由式(12)可得相位误差Δφ和理想相位主值φ之间的关系如式(13)所示
为了改变投影仪投射图案的视觉效果, 普通的商用投影仪的γ值一般大于1, 美国国家电视系统委员会推荐的γ值为2.2, 而投影仪的gamma非线性是摄像机和投影仪引起非线性误差的主要因素[16]. 当γ=2.2,p=0.8(在有环境光的条件下,p<1)时, 由式(6)和式(7)求得B3/B1=0.006 3, 由式(13)可得, Δφ是一个周期函数且 |Δφ|≤0.006 3 rad; 当γ=4.0,p=0.8时,B3/B1=0.099 3, |Δφ|≤0.099 3 rad, |Δφ|随着γ值的增大而增大. 当|Δφ|≤0.099 3 rad 时, 式(12)和式(13) 的差值小于2.419×10-4rad, 在实际测量中可以近似认为式(12)和式(13)等价, 将B3/B1简记为β, 式(13)可简化为
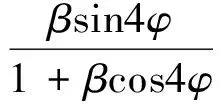
假设Δφ′为
同理, 式(15)可简化为
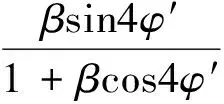
由式(14)和式(16)计算得补偿相位Δφ和Δφ′之差为
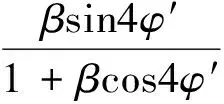
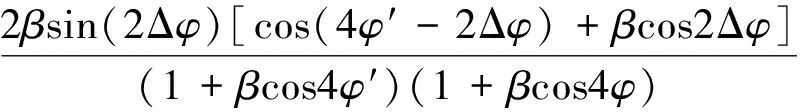
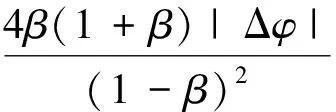
由式(16)可知, 当β=0.006 3(γ=2.2,p=0.8)时, |Δφ′-Δφ|≤0.025 7|Δφ|; 当β=0.054(γ=3.2,p=0.8)时, |Δφ′-Δφ|≤0.255|Δφ|. 当β分别取值为0.006 3(γ=2.2,p=0.8), 0.054 (γ=3.2,p=0.8)和0.099 3(γ=4.0,p=0.8)时, 由式(13)和式(15)计算可得|Δφ′-Δφ|分别小于7.94×10-5, 0.005 2和0.020 8 rad, |Δφ| 分别小于0.006 3, 0.054和0.099 3 rad. 当γ由2.2增大到4.0时, 补偿精度随系统γ值的增大有所降低, 但是仍然能有效减小gamma非线性误差的波动幅度. 因此在实际测量中, 可以由下式近似计算相位误差补偿值
式中:B1和B3分别为变形光栅条纹图像一次谐波和三次谐波的幅值. 由式(6)和式(7)可知,B1和B3与系统的γ和p值有关, 在系统的γ和p值未知的情况下可考虑用频域变换法得到B3. 即对变形光栅条纹图像进行傅立叶变换, 用滤波器取频谱图像的三次谐波后进行傅里叶逆变换, 在物体表面起伏平缓区域的三次谐波的幅值约等于B3.
2 仿 真
为了验证该算法对减小非线性噪声的有效性, 进行了计算机仿真. 计算机生成一个椭圆物体, 如图1(a)所示.
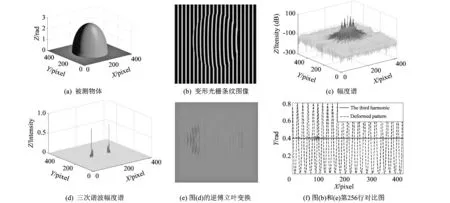
图 1 B3/B1的计算步骤Fig.1 Algorithm steps for B3/B1
采用标准四步相移法, 当γ=2.2,α=1,M=0.5,N=0.4时, 采用式(2)计算的一幅变形光栅条纹图像模拟摄像机采集到的图像, 如图1(b)所示. 对图1(b)进行傅立叶变换, 其频谱如图1(c)所示. 由于三次谐波相对于基波幅度较小, 因此采用分贝(dB)作为单位以清晰地显示三次谐波. 用巴特沃斯滤波器取三次谐波如图1(d)所示. 对图1(d)进行逆傅里叶变换, 得到三次谐波的时域图像如图1(e)所示. 图1(b)和图1(e)第256行对比如图1(f)所示, 在物体表面形状缓变区域的幅度系数B3约为0.005 04 rad, 本次试验中B3/B1约等于0.006 3. 由于图1(d)中没有直流分量, 为了对比基波和三次谐波的幅度大小, 将三次谐波沿着Y轴正方向平移0.4得到图1(b)和1(e)的对比图 (第256行), 如图1(f)所示.
将B3/B1=0.006 3代入式(18)得到相位误差补偿值, 如图2(a)所示. 图2(b)和图2(c)分别是相位补偿前后物体的相位高度图. 图2(d)是图2(b) 和图2(c)第256行对比, 可见相位误差补偿后物体表面的周期性误差明显减小. 图2(e)和图2(f)分别是补偿前后的相位误差分布, 补偿前误差波动幅度为0.006 3 rad, 补偿后误差波动幅度为0.000 354 rad. 当系统的gamma值为2.2时, 采用本文所提方法, 由非线性引起的相位误差的波动幅值减小到补偿前相位误差的波动幅值的1/17以下, 因此采用本方法极大地减小了投影仪和摄像机的非线性引起的相位误差.
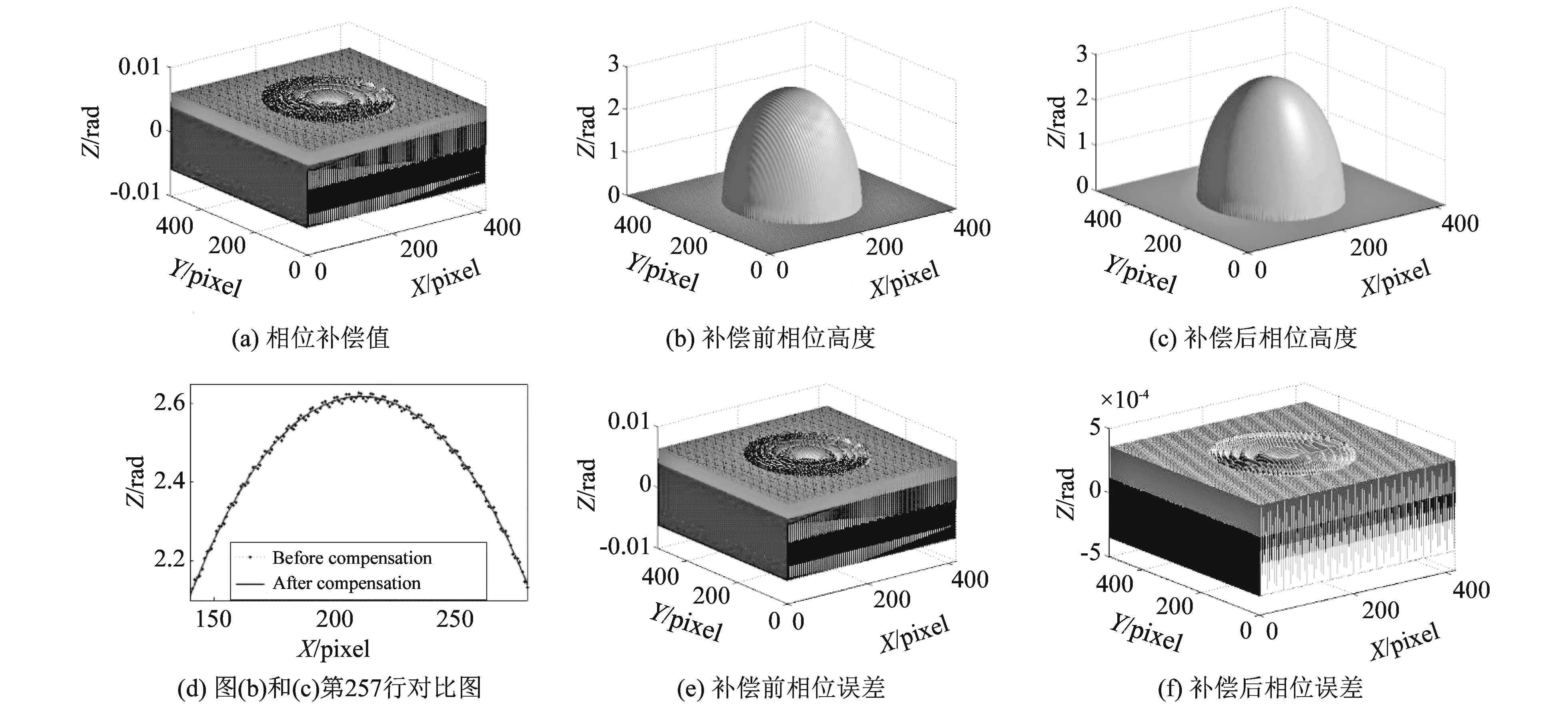
图 2 计算机仿真结果Fig.2 Simulated measurement
3 实 验
为了进一步检验本文所提算法的正确性, 在实验室采用四步相移法对一个边缘形状突变和一个表面形状有明显凹凸变化的物体分别进行测量, 并采用本文所提方法进行相位误差补偿. 本次实验中投影仪和摄像机型号分别为EPSON cb-x18和维视MV-VD200SC; 摄像机和投影仪的分辨率分别为960×1 280和1 024×768. 将摄像机和投影仪放置在距离测量物体约1 m处, 投影仪将4幅初相位相差π/2的正弦光栅条纹图像投射到边缘形状突变的物体表面, 摄像机采集变形的光栅条纹图像, 其中一幅如图3(a)所示, 其幅度谱如图3(b)所示, 可见光栅条纹图像中包含明显的三次谐波. 误差补偿前后的物体相位高度如图3(d)和图3(e)所示, 相位误差补偿后, 物体表面明显光滑. 图3(f)和图3(g)分别是图3(d)和图3(e)的局部放大图(第350行到400行, 第250列到300列, 51×51的区域). 图3(h)是图3(d)和图3(e)的第200行的对比图, 相位误差补偿后的波动幅度明显减小.
在相同的实验条件下, 使用该测量系统对表面形状有明显凹凸变化的物体进行测量. 图4(a)是被测物体, 摄像机采集到的一幅被测物体的变形光栅条纹图像如图4(b)所示, 其幅度谱如图4(c)所示; 图4(d)和图4(e)分别是误差补偿前后的相位高度图; 图4(f)和图4(g)分别是图4(d)和图4(e)的局部放大图(第150行到200行, 第80列到120列, 51×41的区域), 可见误差补偿后物体表面的周期性误差得到了明显的抑制; 图4(h)是图4(f)和图4(g)的第6行的对比图, 可见补偿后的周期性相位误差波动幅度明显减小.
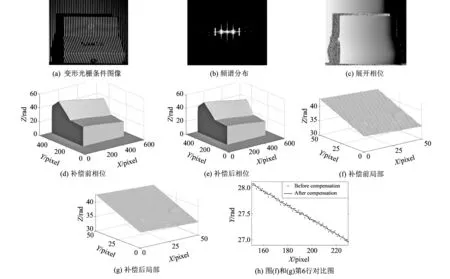
图 3 实验结果1Fig.3 Experimental resuts (1)
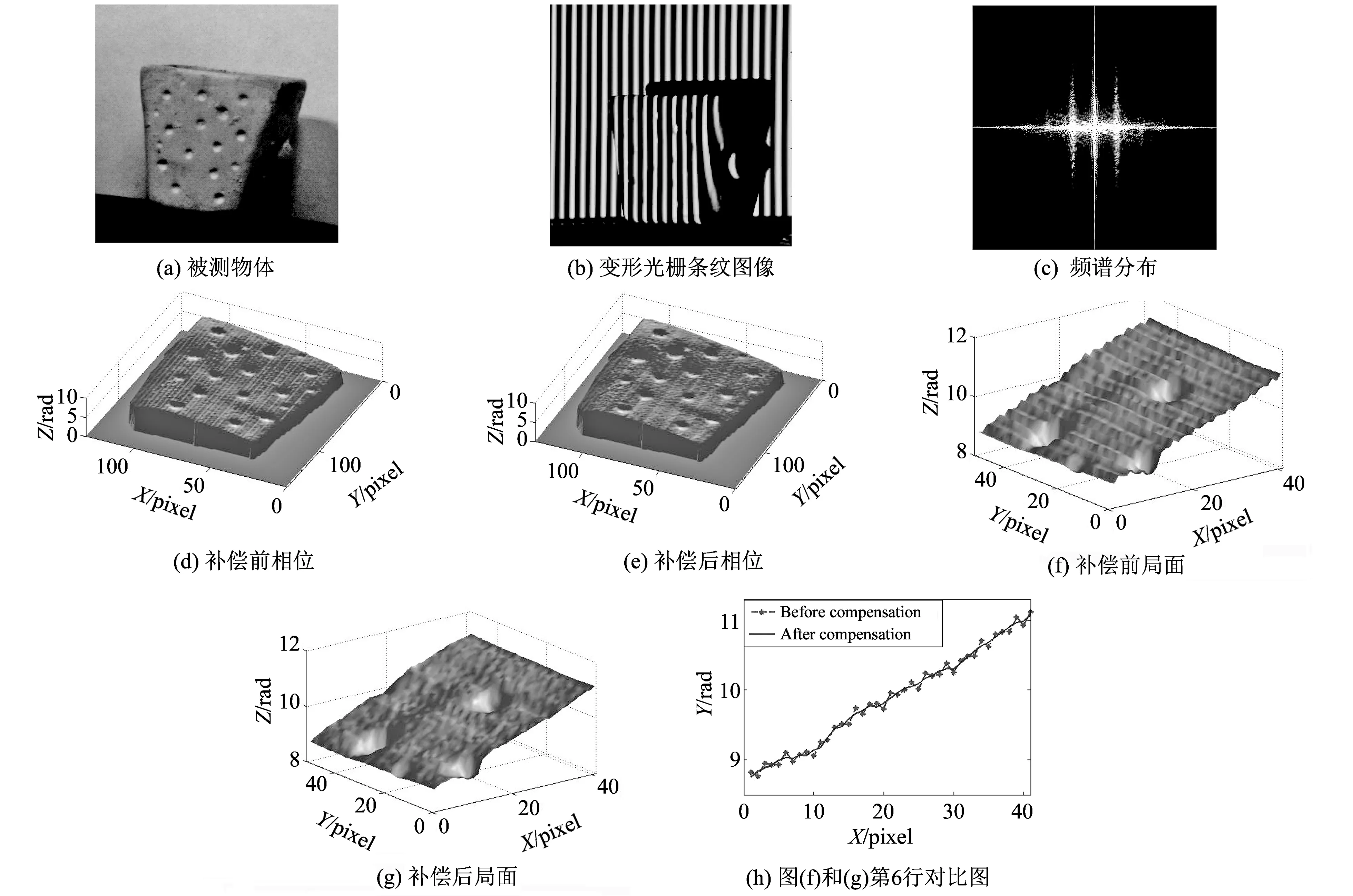
图 4 实验结果2Fig.4 Experimental resuts (2)
为了进一步确定该方法的测量精度, 在相同的实验条件下, 使用该测量系统对一个平面白板进行相位展开和补偿实验. 图5(a)是摄像机采集到的一幅变形光栅条纹图像, 其幅度谱如图5(b)所示; 误差补偿前后的平面的展开相位高度如图5(d)和图5(e)所示; 图5(f)和图5(g)分别是图5(d)和图5(e)的局部放大图(第100到150行, 第130到180列, 51×51的区域); 图5(h)是图5(f)和图5(g)的第6行对比图. 误差补偿前后, 相位误差的最大值分别是0.086 7 rad和0.030 8 rad; 相位补偿前后平面白板展开相位的均方根(RMS)分别是0.035 rad和0.007 rad.
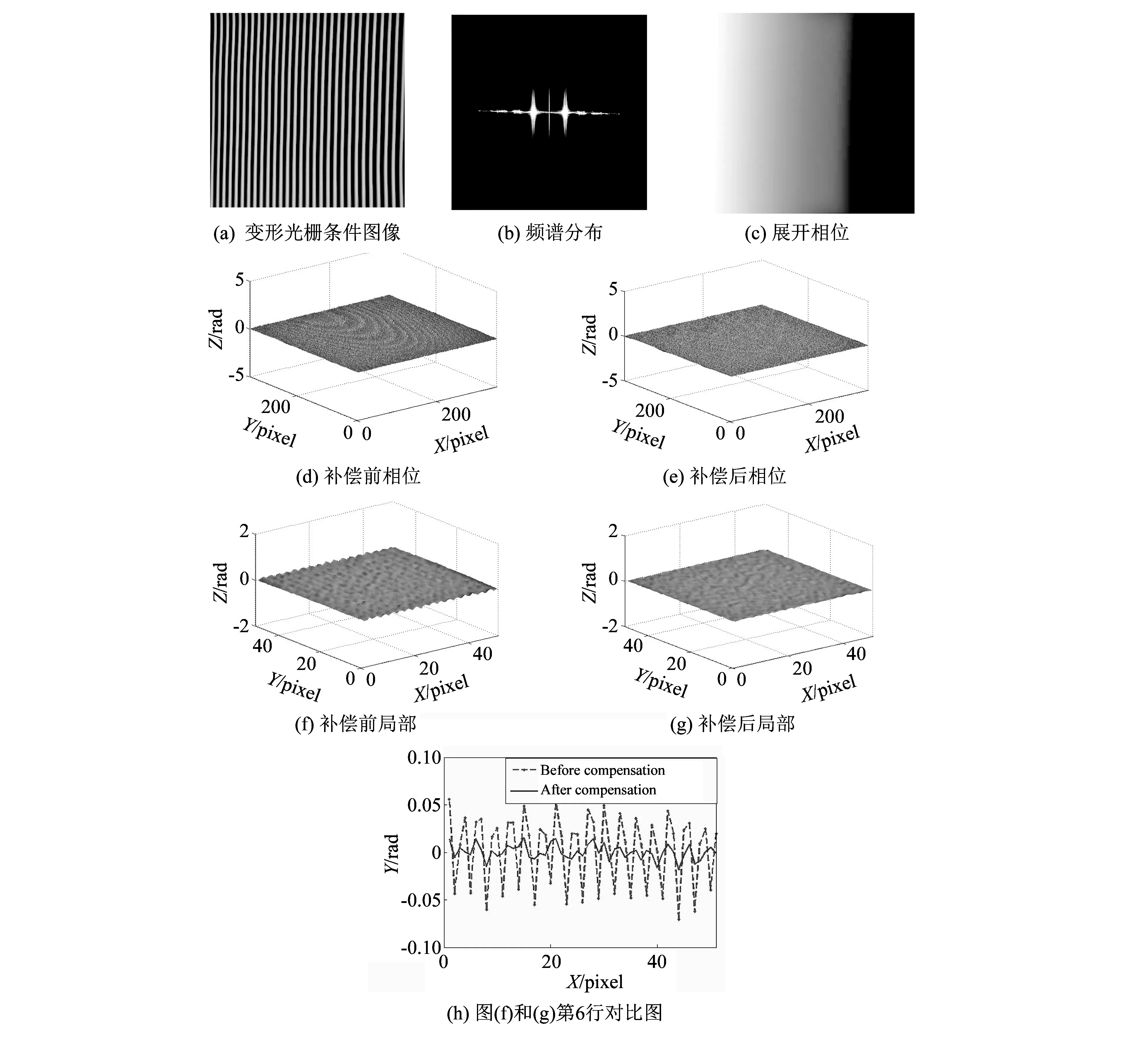
图 5 测量精度实验结果Fig.5 Experimental results of measurement accuracy
4 结 论
本文建立了四步相移法的gamma非线性相位误差和相位主值(包含相位误差的相位主值)之间的关系模型, 并用三次谐波的逆傅立叶变换估计了变形光栅条纹图像中的三次谐波幅值. 仿真实验证明, 当系统的gamma值为2.2时, 使用本方法补偿相位误差后, 误差波动幅度降低到原来波动幅度的1/17; 实验证明, 一个平面白板的展开相位的RMS在误差补偿前后分别是0.035 rad和0.007 rad, 误差补偿后, 平面白板展开相位的最大误差从0.086 7 rad降低到0.030 8 rad. 使用本文所提方法有效减小了四步相移法由系统gamma非线性引起的周期性相位误差.
[1] Park Y, Scaffardi M, Poti L. Simultaneous single-shot real-time measurement of the instantaneous frequency and phase profiles of wavelength-division-multiplexed signals[J]. Optics Express, 2010,18(6): 6220-6229.
[2] Lei H, Chang X Y, Wang F, et al. A novel algorithm based on histogram processing of reliability for two-dimensional phase unwrapping[J]. Optik, 2015, 126(18): 1640-1644.
[3] Song K C, Hu S P, Wen X, et al. Fast 3D shape measurement using Fourier transform profilometry without phase unwrapping[J]. Optics and Lasers in Engineering, 2016, 84: 74-81.
[4] Peng K, Cao Y P, Wu Y C, et al. A new method using orthogonal two-frequency grating in online 3D measurement[J]. Optics and Laser Technology, 2016, 83: 81-88.
[5] Song L M, Chang Y L, Xi J T, et al. Phase unwrapping method based on multiple fringe patterns without use of equivalent wavelengths[J]. Optics Communications, 2015, 355(15) : 213-224.
[6] Huang H F. A fast multi-baseline and multi-frequency band phase-unwrapping algorithm[J]. Measurement, 2014, 49: 401-406.
[7] Din I, Anwar H, Syed I H, et al. Projector calibration for pattern projection systems[J]. Journal of Applied Research and Technology, 2014, 12(1): 80-86.
[8] Chen Y J, Wang K Q, Zuo W M, et al. A novel projector calibration method based on improved two-frequency grating projection[J]. ICIC Express Letter B , 2012, 3(1): 71-76.
[9] Ye X, Cheng H B, Wu H Y, et al. Gamma correction for three-dimensional object measurement by phase measuring profilometry[J]. Optik, 2015, 126(24): 5534-5538.
[10] Hoang T, Pan B, Nguyen D, et al. Generic gamma correction for accuracy enhancement in fringe-projection profilometry[J]. Optics Letters, 2010, 35(12): 1992-1994.
[11] 许伟, 陈晓波, 习俊通. 结构光测量相位波动误差补偿方法研究[J]. 光学学报, 2011, 31(3): 133-138.
Xu Wei, Chen Xiaobo, Xi Juntong. A method of phase error compensation for structural light measurement[J]. Acta Optica Sinica, 2011, 31(3): 133-138. (in Chinese)
[12] Zhou P, Liu X R, He Y, et al. Phase error analysis and compensation considering ambient light for phase measuring profilometry[J]. Optics and Lasers in Engineering, 2014, 55: 99-104
[13] 周平, 朱统晶, 刘欣冉, 等. 结构光测量中相位误差的过补偿与欠补偿校正[J]. 光学精密工程, 2015, 23(1): 56-62.
Zhou Ping, Zhu Tongjing, Liu Xinran, et al. Correction of phase error overcompensation and under-compensation in structured light measurement[J]. Optics and Precision Engineering, 2015, 23(1): 56-62. (in Chinese)
[14] Lei Z K, Wang C L, Zhou C L. Multi-frequency inverse-phase fringe projection profilometry for nonlinear phase error compensation[J]. Optics and Lasers in Engineering, 2014, 66 (3): 249-257.
[15] 钟凯. 基于多视相移框架的动态物体三维面形测量技术与系统研究[D]. 武汉: 华中科技大学, 2013.
[16] Zhang S, Yau S. Generic non-sinusoidal phase error correction for three-dimension shape measurement using a digital video projector[J]. Applied Optics, 2007, 46(1): 36-43.
ACompensationApproachofPhaseErrorsCausedbyGammaNonlinearityforFour-StepPhase-ShiftingAlgorithm
ZHAO Xian-ling1,2, LIU Jian-sheng1, ZHANG Hua-yu1, WU Ying-chun2
(1. College of Material Science and Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China; 2. College of Electronics and Information Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)
Gamma nonlinearity of the projector-camera pair is a main source of phase error about phase measuring pro-filometry(PMP). It causes higher-order harmonics in deformed pattern captured by camera and leads to periodic phase error at unwrapped phase map. For four-step phase-shifting algorithm, the third harmonic is the main reason which leads to appearance of periodic phase error. In order to decrease the phase error caused by gamma nonlinearity, the model between phase error and wrapped phase was established and a phase error compensation method was proposed under the condition of gamma value unknown. The simulated measurement shows that the volatility of phase error before and after compensation is less than 0.0063 rad and 0.000354 rad respectively (γ=2.2,p=0.8). The experimental results show that RMS of unwrapped phase before and after compensation about a uniform is 0.035 rad and 0.007 rad respectively and the maximum phase error decrease from 0.0867 rad to 0.0308 rad after compensation.
phase error compensation; four-step phase-shifting algorithm; gamma nonlinearity; the third harmonic; coefficient of harmonic
1673-3193(2017)03-0373-07
2016-10-28
国家自然科学基金青年科学基金资助项目(61601318 ); 山西省青年科技研究基金资助项目(201601D021078)
赵贤凌(1978-), 女, 讲师, 博士生, 主要从事非接触三维测量方法的研究.
TN253
A
10.3969/j.issn.1673-3193.2017.03.021

