基于分数阶各向异性扩散和小波的MLEM低剂量CT重建算法*
焦枫媛, 韩 燮, 常 皓
(1. 中北大学 计算机与控制工程学院, 山西 太原 030051; 2. 中北大学 信息商务学院, 山西 晋中 030600;3. 中国人民解放军63961部队, 北京 100012)
基于分数阶各向异性扩散和小波的MLEM低剂量CT重建算法*
焦枫媛1,2, 韩 燮1, 常 皓3
(1. 中北大学 计算机与控制工程学院, 山西 太原 030051; 2. 中北大学 信息商务学院, 山西 晋中 030600;3. 中国人民解放军63961部队, 北京 100012)
针对低剂量CT重建图像受噪声污染严重的问题, 提出了一种基于分数阶各项异性扩散和小波的MLEM低剂量CT重建算法. 首先, 采用最大似然期望最大化(Maximum Likelihood Expectation Maximization, MLEM)算法重建低剂量投影数据. 然后, 将小波变换应用于图像, 使得图像的低频系数部分集中了主要信息, 而高频系数部分集中了边缘和噪声. 最后, 在低频系数部分进行基于差分的分数阶各项异性扩散, 在高频系数部分进行软阈值处理. 采用Shepp-Logan和Hot-Cold模型进行低剂量CT图像重建仿真, 实验结果表明, 本文算法在降低噪声和保持图像细节方面都优于其他算法.
分数阶微分; 各项异性扩散; 小波变换; 低剂量CT; 图像重建
0 引 言
计算机断层扫描(Computed Tomography, CT)技术在疾病预防、 临床诊断中有着巨大的作用. X射线放射剂量的增高可以提高重建图像的质量, 但这种高剂量带来的高辐射又会对人体健康造成极大的危害; 而降低剂量, 又必然会使得重建图像噪声增加, 进而影响医疗诊断的准确度. 因此, 如何在降低辐射剂量的同时得到高质量的CT重建图像成为当前的一个热门问题, 对该问题的研究也越来越受到人们的重视[1].
针对低剂量CT重建图像的退化问题, 研究学者已经提出了很多策略. 一是投影域降噪, 即先对图像的投影数据进行降噪, 再对降噪后的数据进行重建. 如Wang等[2]通过在小波域中采用惩罚加权最小二乘滤波算法大大提高了重建图像的质量; Zhang等[3]提出的基于各项异性扩散的加权先验方法实现了对贝叶斯统计的正弦图的有效降噪, 而且边缘和细节信息得到了很好的保持; 李凯旋等[4]提出的基于投影数据恢复导引的双边滤波权值优化方法进一步保持了图像细节信息. 二是图像后处理方法, 即在重建后对得到的图像进行降噪. 后处理的方法可以根据图像的不同特征而采取不同的方法, 由于其方便实用而成为近年来研究的一个热点. 许多有效的滤波算法被应用于低剂量CT图像处理中, 并取得了较好的效果. 如Chen等[5-6]提出了一种基于字典学习的低剂量CT图像伪影去除算法和降低脑部CT辐射剂量的字典学习算法, 有效改善了低剂量CT图像的质量; Rust等[7]利用非线性高斯滤波器链对重建图像进行平滑处理; Paul等[8]提出的基于特征的低剂量胸部CT图像噪声降低方法, 可以对不同的组织结构采取不同的降噪方法, 从而在减少伪影的同时很好地保持图像的细节信息; Zhang等[9-10]首次将分数阶微积分应用于医学图像处理, 并提出了两个用于降低CT图像金属伪影的分数阶方程, 使得图像细节信息得到了进一步保持.
基于以上分析和研究, 本文提出了一种基于分数阶各项异扩散和小波的MLEM 低剂量CT重建算法. 该算法首先对低剂量投影数据进行最大似然期望最大化算法重建, 然后对重建图像进行小波分解, 在小波低频系数部分, 采用基于方差的分数阶各项异性扩散, 在高频系数部分, 运用阈值降噪进行处理. 采用Shepp-Logan和Hot-Cold模型进行仿真实验, 通过与其他算法进行比较, 本文算法重建图像不但取得了最高的信噪比, 而且在降低噪声的同时在视觉效果上也有效地保持了图像的细节和边缘信息.
1 分数阶微积分
分数阶微积分有空域和频域两大类定义, 其中应用最广泛的是Grümwald-Letniklv (G-L)定义和 Riemann- Liouville (R-L) 定义. 本文在图像处理中应用到的是G-L定义, 信号f(x)的α阶微分的G-L定义如下[11]
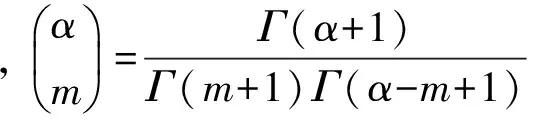
2 基于分数阶各项异性扩散和小波的MLEM低剂量CT重建算法
2.1 最大似然期望最大化重建算法
最大似然期望最大化(Maximum Likelihood Expectation Maximization, MLEM)算法通常会在重建过程中考虑到观测数据的统计特性和系统的物理模型, 因此, 与滤波反投影(Filtexed Back Projection, FBP)重建算法比较, 该算法重建效果明显更好, 其重建公式如下[12]
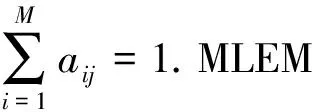
2.2 基于分数阶各项异性扩散和小波的降噪方法
2.2.1 整数阶各项异性扩散算法
Perona等[13]在1990年提出了各项异性扩散方程(PM模型), 其表达式为
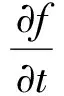
式中:c为扩散系数函数, 其表达式为
c(|f|)=1/[1+|
式中:k为梯度阈值. PM模型能够在有效去除噪声的同时保持图像边缘信息, 但去噪后的图像往往会出现块状效应.
为了克服块状效应, You等[14]在2000年提出了一类四阶偏微分方程, 其在一定程度上抑制了块状效应, 但是又产生了斑点效应.
2.2.2 基于方差的分数阶各项异性扩散算法
为了解决以上问题, Bai等[15]在2007年提出了分数阶各项异性扩散方程, 其能量函数表示为

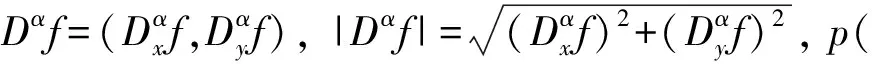
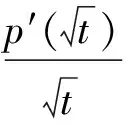
当α=1时, 式(5) 近似于 PM模型, 当α=2时, 式(5)近似于四阶扩散方程, 当1<α<2时, 式(5)可以看作二阶和四阶各项异性扩散的一个插值. 分数阶各项异性扩散算法在降低噪声的同时有效抑制了阶梯效应和斑点效应.
为了更好地保持图像细节和边缘信息, 本文将可以较好区分细节和平坦区域的局部方差加入到分数阶各项异性扩散方程的扩散系数中. 由文献[16]可知归一化的方差可表示为
其中:
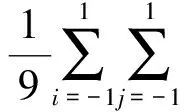
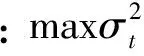
此时, 分数阶各项异性扩散模型中扩散系数为
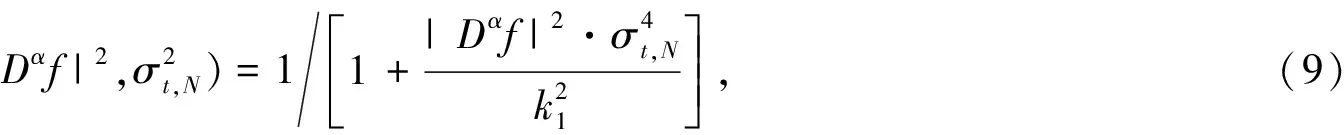
式中:k1为常数.
应用文献[17]中分数阶微分的离散化方法, 将分数阶微分看作卷积积分, 于是式(5)变为

其中:
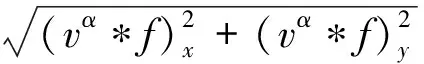


利用梯度下降法, 可以得到
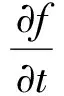
首先对(vα*f)x和(vα*f)y进行离散化
记:
这里为了保证分母不为零,ε取很小的整数. 基于方差的分数阶各项异性扩散方程的离散化形式为
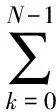
2.2.3 小波阈值降噪
噪声和表示图像特征的细节信息都属于高频成份, 因此在降低噪声的图像处理过程中往往会带来细节信息的丢失. 针对这一问题, 人们在图像去噪中广泛采用小波变换, 因为其具有时频局部化和多分辨率特性. 而在小波域中, 表示噪声的系数会随着尺度的增加而减小, 表示信号的系数会随着尺度的增加而增加[18]. 所以, 小波分解之后, 绝对值比较大的高频小波系数需要保留, 因为其主要由原始图像信号提供; 绝对值比较小的高频小波系数需要滤除, 因为其主要由噪声提供. 在小波阈值降噪过程中, 通过对小波系数进行阈值处理可以使重建图像中有用的信息得到很好的保持, 因此, 合适的阈值选择至关重要.
2.3 重建算法
经过小波变换之后, 低频部分集中了图像的主要信息, 而边缘和噪声信息属于高频分量. 由于噪声对分数阶各项异性扩散影响较大, 所以在含有噪声较少的低频分量中采用分数阶各项异性扩散来降噪, 就可以避免噪声对其造成的影响. 另外, 分数阶各项异性扩散需要较大的计算量, 而小波变换收敛速度很快. 因此, 本文结合了二者的优点, 在降噪过程中运用了混合降噪方法, 即在低频分量部分采用基于方差的分数阶各项异性扩散, 在高频分量部分采用小波变换软阈值去噪. 本文重建算法的具体步骤如下:
1) 在理想投影数据中加入噪声变为低剂量投影数据, 再根据式(2)对其进行最大似然期望最大化算法重建.
2)在每次迭代中, 将多尺度小波变换应用于MLEM重建图像中, 由此生成的低频分量为CAi, 高频分量记为CHi,CVi,CDi, 其中i=1,2,3,…,n, 为分解尺度.
3) 选择合适的阈值, 对高频系数进行小波阈值降噪.
4) 将基于方差的分数阶各项异性扩散降噪算法应用于低频系数中. 由式(12)~式(14), 可得迭代公式为
5) 进行小波反变换得到去噪后的图像.
6) 不断重复以上步骤, 最终获得理想的重建图像.
3 实验结果及分析
3.1 重建图像比较
为了直观地证明本文算法的有效性, 仿真实验中采用了2个模型数据: 模型1为Shepp-Logan头部剖面图模型, 模型2为模拟人体骨骼组织和软组织的Hot-Cold 模型, 模型大小均为128×128, 系统矩阵大小为 (128×128) ×(128×128). Li等[19]的实验结果表明: 低剂量投影数据的噪声是期望和方差成非线性关系的高斯噪声, 其表达式如下
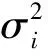
如图 1 所示, 本文除了将传统的MLEM、 BI- MLEM(Block Iterative-Maximum Likelihood Expectation Maximization)[20]重建算法与本文算法进行比较, 还将经典的PM、 TV算法应用到MLEM重建算法中, 分别形成了PM-MLEM和TV-MLEM算法, 并与本文算法进行了比较.
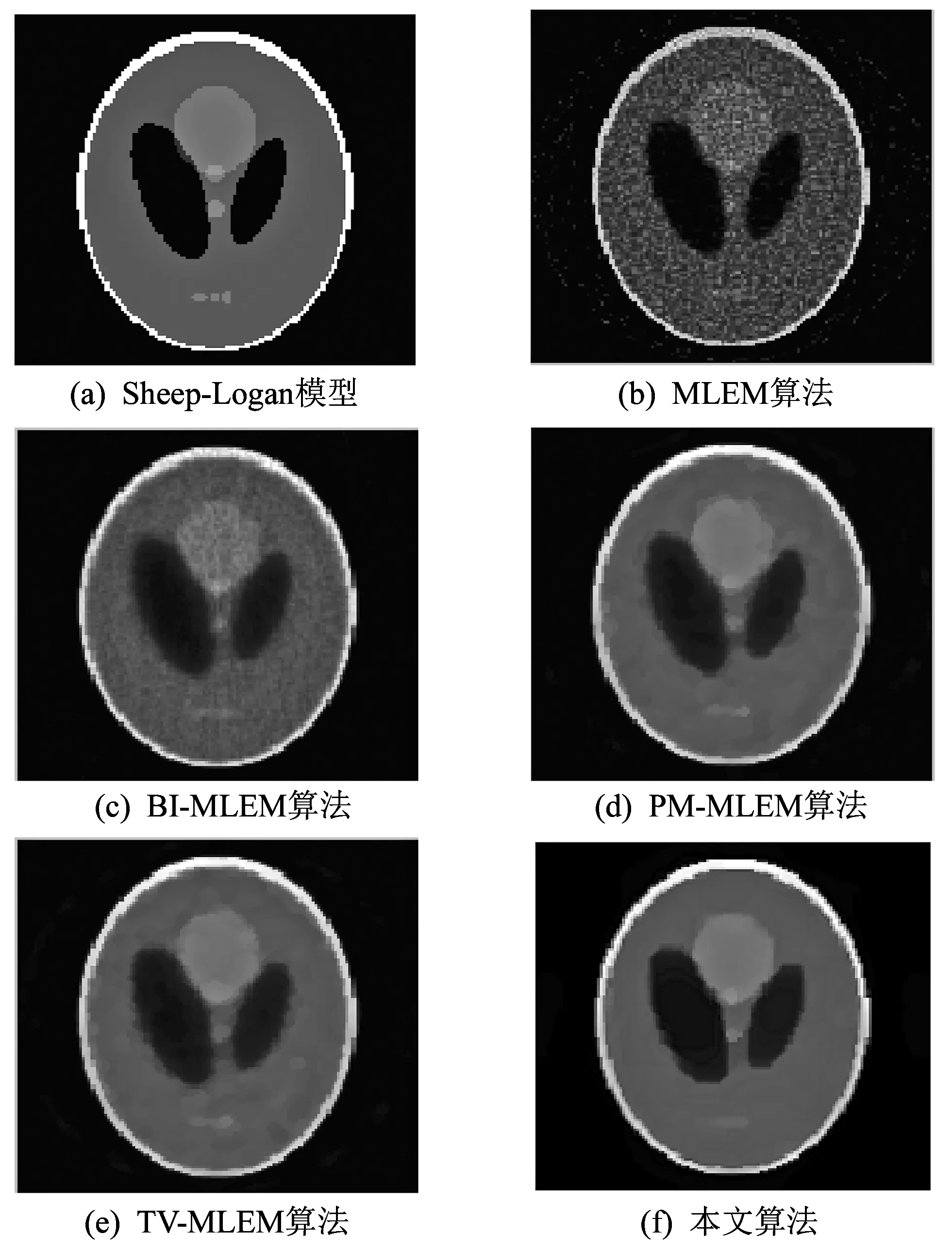
图 1 Shepp-Logan模型比较实验Fig.1 The comparative experiments on Shepp-Logan model
通过观察图 1 中Shepp-Logan头部模型原图及其重建图像可以发现, MLEM和BI- MLEM重建图像含有大量噪声, 视觉效果非常差, 所以这两种算法不适合应用于低剂量CT图像重建. PM-MLEM和TV-MLEM重建图像中包含更少的噪声, 但是出现了明显的块状效应. 从视觉效果上看, 本文算法重建图像中包含的噪声和条形伪影最少, 基本看不到块状效应, 图像细节和纹理保持也比较好. 因此, 本文算法在低剂量CT图像重建中的表现明显优于其它4种算法.
为了进一步验证本文算法的可行性, 采用Hot-Cold 模型进行实验. 从图 2 中Hot-Cold 模型原图及其重建图像可以看到, MLEM重建图像含有最多的噪声, 重建效果很差. BI-MLEM重建图像仍然含有大量噪声, 而PM-MLEM和TV- MLEM重建图像中噪声大幅下降, 但是能看到明显的条形伪影和块状效应. 本文算法重建图像在噪声降低和细节、 纹理保持方面都是最好的, 视觉效果最接近原图. 比较其他算法, 本文算法在降低噪声的同时保持了更多的细节信息, 因此更适合应用于低剂量CT图像处理.
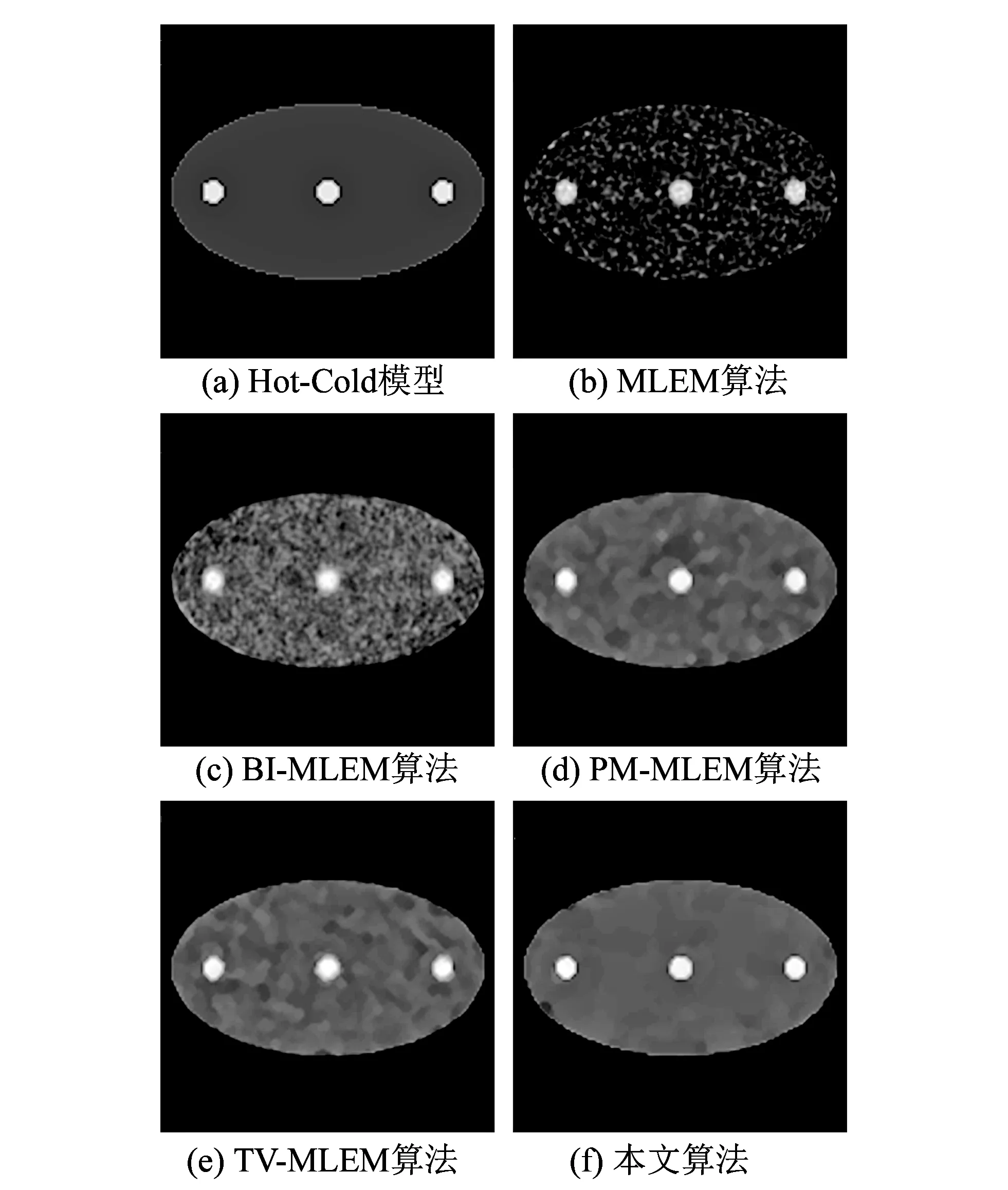
图 2 Hot-Cold模型比较实验Fig.2 The comparative experiments on Hot-Cold model
3.2 重建精度分析
从上述视觉效果分析可知, 本文算法对低剂量CT图像有很好的处理效果. 为了进一步客观上定量地说明本文算法在医学图像处理中的可行性, 采用归一化均方误差、 均方绝对误差、 信噪比对重建图像质量进行定量描述. 其定义表述如下:
1) 归一化均方误差(NMSE)
2) 均方绝对误差(MAE)
).
(17)
3) 信噪比(SNR)
式中:Mi和mi分别为重建图像与真实图像的均值;Fi和qi分别为重建图像与真实图像的第i个像素的灰度值;M和N分别为图像的行数和列数. NMSE和MAE值越小, 重建图像越接近于真实图像; SNR的值越高, 重建图像质量越好.
本文算法与其他几种算法应用于Shepp-Logan模型和Hot-Cold 模型的客观评价结果如表 1 所示.
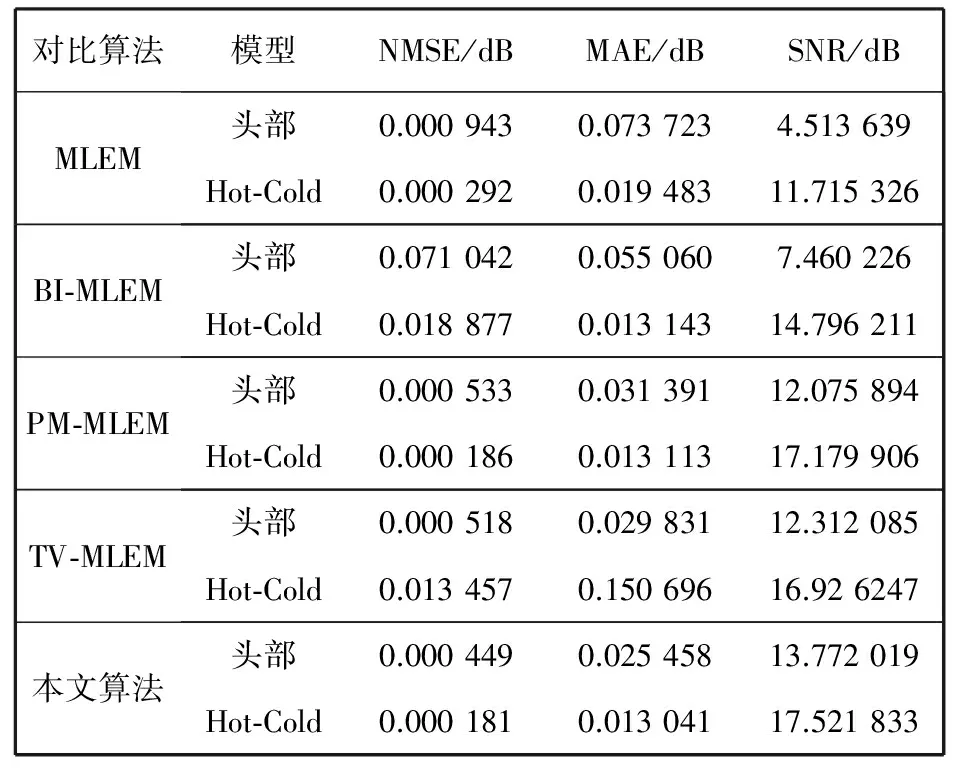
表 1 Shepp-Logan和Hot-Cold 模型各种算法的客观评价
从表 1 可以明显看出, 本文算法的信噪比SNR最大, 说明重建图像中含有最少的噪声, 而本文算法的归一化均方误差NMSE和均方绝对误差MAE均为最小, 说明本文算法重建图像与真实图像最接近. 因此, 本文算法重建图像质量是最好的. 从图1、 图2和表1可以看出, 本文算法无论在视觉效果还是在定量分析方面均优于其他算法.
为了更加直观地比较本文算法与其他4种算法重建图像与原始图像之间的差距, 本文给出了Shepp-Logan模型的原始理想图像与另外几种重建算法结果图像的侧面轮廓线比较图, 并比较了第65行的灰度值, 如图 3 所示.
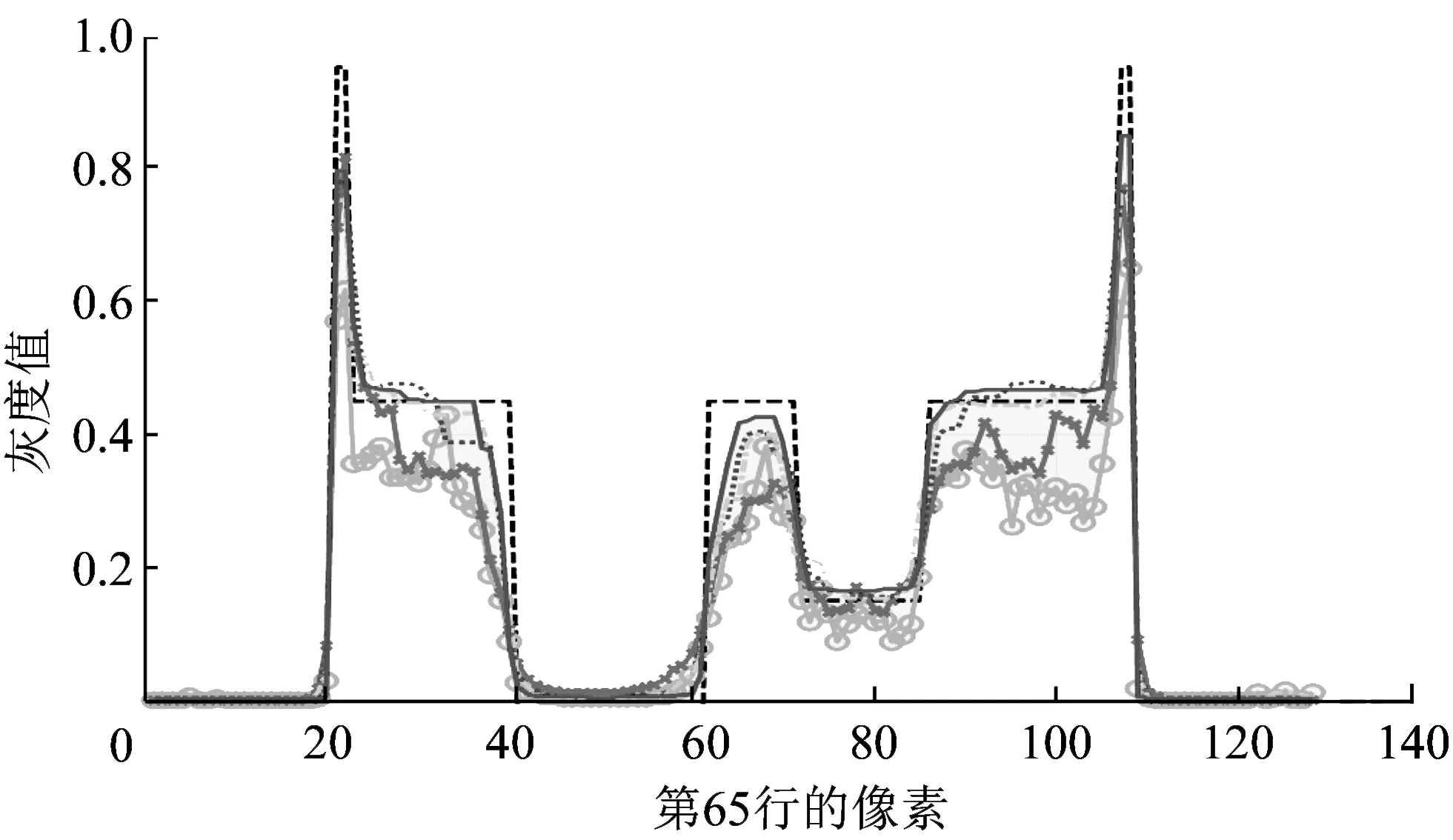
图 3 各种算法重建图像第65行截面图对比Fig.3 Comparison of the profiles on line 65 of processed image by using various algorithms
从图 3 可以看出, 与其他几种算法相比, 本文算法重建出的图像最接近理想图像, 并且在降低噪声和保持图像细节方面效果都最好.
4 结 论
本文基于分数阶各项异性扩散和小波阈值, 提出了一种基于分数阶各项异性扩散和小波的MLEM低剂量CT重建算法. 由于分数阶各项异性扩散对噪声比较敏感, 所以本文算法在对低剂量投影数据进行MLEM重建之后, 对重建图像进行小波分解, 然后在低频分量部分采用基于方差的分数阶各项异性扩散, 在高频分量部分采用小波变换软阈值去噪. 与此同时, 传统的各项异性扩散容易引起块状效应, 本文采用分数阶各项异性扩散, 有效去除了块状效应. 另外, 本文在扩散系数中加入方差项, 进一步保持了图像细节和纹理. 仿真实验结果表明, 本文算法在降低噪声和保持图像细节方面都优于其他算法. 因此, 基于分数阶各项异性扩散和小波的MLEM重建算法适合应用于医学图像处理.
[1] Bian J G, Yang K, Boone J M, et al. Investigation of iterative image reconstruction in low-dose breast CT[J]. Physics in Medicine and Biology, 2014, 59(11): 2659-2685.
[2] Wang J, Lu H B. Multiscale penalized weighted least-squares sonogram restoration for low-dose X-Ray computed tomography[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(3): 1022-1032.
[3] Zhang Q, Gui Z G, Chen Y, et al. Bayesian sinogram smoothing with an anisotropic diffusion weighted prior for low-dose X-ray computed tomography[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(17): 2811-2816.
[4] 李凯旋, 黄静, 马建华, 等. 低剂量CT重建中的双边滤波权值优化新方法[J]. 电路与系统学报, 2012, 17(2): 94-99.
Li Kaixuan, Huang Jing, Ma Jianhua, et al. Bilateral filtering weights optimization in low-dose computed tomography image reconstruction[J]. Journal of Circuits and Systems, 2012, 17(2): 94-99. (in Chinese)
[5] Chen Y, Shi L, Feng Q, et al. Artifact suppressed dictionary learning for low-dose CT image processing[J]. IEEE Transactions on Medical Imaging, 2014, 33(12): 2271-2292.
[6] Chen Y, Shi L, Yang J, et al. Radiation dose reduction with dictionary learning based processing for head CT[J]. Australasian Physical & Engineering Sciences in Medicine, 2014, 37(3): 483-493.
[7] Rust G F, Aurich V, Reiser M. Noise dose reduction and image improvements in screening virtual colonoscopy with tube currents of 20 mAs with nonlinear Gaussian filter chains[C]. Medical Imaging 2002 Conference, New York: IEEE, 2002: 186-197.
[8] Paul N S, Blobelj J, Prezelj E, et al. The reduction of image noise and steak artifact in the thoracic inlet during low dose and ultra-low dose thoracic CT[J]. Physics in Medicine and Biology, 2010, 55(5): 1363-1380.
[9] Zhang Y, Pu Y F, Hu J R, et al. A new CT metal artifacts reduction algorithm based on fractional-order sinogram inpainting[J]. Journal of X-Ray Science and Technology, 2011, 19(3): 373-384.
[10] Zhang Y, Pu Y F, Hu J R, et al. Efficient CT metal artifacts reduction based on fractional-order curvature diffusion[J]. Computational & Mathematical Methods in Medicine, 2011(12): 173748.
[11] Pu Y F, Wang W X, Zhou J L, et al. Fractional differential approach to detecting texture features of digital image and its fractional differential filter implementation[J]. Science China Information Sciences, 2008, 51(9): 1319-1339.
[12] 张权, 付学敬, 桂志国, 等. 基于小波和各向异性扩散的PET图像MLEM重建算法[J]. 计算机应用与软件, 2013, 30(11): 50-53.
Zhang Quan, Fu Xuejing, Gui Zhiguo, et al. MLEM reconstrution algorithm for PET image based on wavelet and anisotropic diffusion[J]. Computer Applications and Software, 2013, 30(11): 50-53. (in Chinese)
[13] Perona P, Malik J. Scale space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.
[14] You Y L, Kaveh M. Fourth-order partial differential equations for noise removal[J]. IEEE Transactions on Image Processing, 2000, 9(10): 1723-1730.
[15] Bai J, Feng X C. Fractional-order anisotropic diffusion for image denoising[J]. IEEE Transactions on Image Processing, 2007, 16(10): 2492-2502.
[16] Chao S M, Tsai D M. An improved anisotropic diffusion model for detail and edge-preserving smoothing Pattern Recogn[J]. Pattern Recognition Letters, 2010, 31(13): 2012-2023.
[17] Wang Y L, Shao Y L, Gui Z G, et al. A novel fractional-order differentiation model for low-dose CT image processing[J]. IEEE Access, 2016, 4: 8487-8499.
[18] Liu J, Moulin P. Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients[J]. IEEE Transactions on Image Processing, 2001, 10(11): 1647-1658.
[19] Li T, Li X, Wang J, et al. Nonlinear sonogram smoothing for low-dose X-ray CT[J]. IEEE Transactions on Nuclear Science, 2004, 51(5): 2505-2513.
[20] Byrne C L. Block-iterative methods for image reconstruction from projections[J]. IEEE Transactions on Image Processing, 1996, 5(5): 792-794.
TheMLEMLow-DoseCTReconstructionAlgorithmBasedonFractional-OrderAnisotropicDiffusionandWavelet
JIAO Feng-yuan1,2, HAN Xie1, CHANG Hao3
(1. School of Computer Science and Control Engineering, North University of China, Taiyuan 030051, China;2. College of Information and Business, North University of China, Jinzhong 030600, China; 3. PLA Unit 63961, Beijing 100012, China)
Concerning the noise problem about reconstructed images of low-dose CT, a MLEM low-dose CT reconstruction algorithm based on fractional-order anisotropic diffusion and wavelet was proposed. Firstly, the MLEM algorithm was used to do reconstruction of the low-dose projection data. Secondly, by the wavelet transformation, the main information of image was concentrated in the low frequency coefficients, and the edge and noise was stored in the high frequency coefficients. Finally, the low frequency coefficients of the image were filtered by fractional-order anisotropic diffusion based on difference, and the high frequency coefficients were processed by the soft threshold function. Shepp-Logan and Hot-Cold model were used for low-dose CT reconstruction simulation. The experimental results demonstrate that compared with other methods, the proposed algorithm achieves superior performance in terms of both noise suppression and detail preservation.
fractional-order differentiation; anisotropic diffusion; wavelet transform; low-dose computed tomography(CT); image reconstruction
1673-3193(2017)03-0348-06
2016-08-16
山西省重点研发计划资助项目(201603D121012)
焦枫媛(1992-), 女, 硕士生, 主要从事图像处理及计算软件的研究.
TP391.41
A
10.3969/j.issn.1673-3193.2017.03.017

