线性规划问题非有效变量判别定理的研究*
高引民, 陈建斌
(北京联合大学 商务学院, 北京 100025)
线性规划问题非有效变量判别定理的研究*
高引民, 陈建斌
(北京联合大学 商务学院, 北京 100025)
为完善线性规划模型的基本理论, 通过分析线性规划模型中变量与约束条件的关系, 非有效变量与最优解的关系, 对线性规划模型中非有效变量和有效变量的特性进行了理论探讨, 获得了识别非有效变量的一些判定定理, 为构造识别非有效变量的方法提供了理论基础.
线性规划; 可行域; 非有效变量; 非有效约束条件
0 引 言
为迎接多变的市场带来的挑战, 企业越来越依靠对信息的占有, 对企业整体状况的把握, 以及对企业资源的优化配置, 这都需要借助线性规划来做出最优的决策, 其在经济、 工程、 军事和农业等方面有着极为广泛的应用. 近年来, 线性规划的理论和求解方法无论从广度和深度都取得了重大的进展, 为线性规划的应用及进一步发展奠定了基础. 科学技术与计算机技术的发展将为线性规划的应用提供了更好的环境, 同时也对其提出了新的要求.
在将具体应用的实际问题需要转化为利用线性规划模型来解决的过程中, 由于具体问题的复杂性可能使不具有有效约束的条件和决策变量都被引进来, 这就造成了线性规划问题模型中的约束条件的数量大大增加, 而整个求解线性规划问题的工作量和复杂度都与线性规划的约束规模相关. 文献[1]从线性规划对偶问题的角度出发, 对应用对偶性进行数据预处理的方法做了总结, 并研究了基于对偶性理论的方法在预处理中的效用, 尤其是针对大规模线性规划问题. 线性规划的研究直接推动了其他数学规划问题包括整数规划、 随机规划和非线性规划的算法研究[2]. 通过求解线性规划问题的基本解来逼近最优解是求解线性规划问题的方法体系中非常重要的一类方法, 称为基点上迭代逼近最优解方法, 它包括线性规划问题单纯形法, 对偶单纯形法, 原始-对偶单纯形法, 松弛法等, 将摄动算法和亏基原始单纯形算法相结合, 采用最陡边的列主元规则, 可以充分发挥这两种算法的优势[3-8]. 而识别线性规划模型中非有效约束方程及非最有效约束方程的理论[9-10], 对于缩小原模型的规模、 降低原模形的复杂性、 求解线性规划都是有益的. 同样, 识别非有效变量的理论及变量与约束条件的关系理论都是有价值的. 本文对线性规划模型中的变量性质进行研究, 分析了变量与约束条件的关系, 并对非有效变量与变量及变量与最优解的关系进行了分析与探讨.
1 定义及引理

对于线性规划问题(LP)



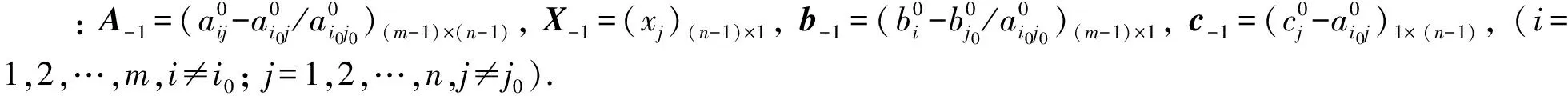
显然,LP-1变量的个数为n-1, 约束条件的个数为m-1.
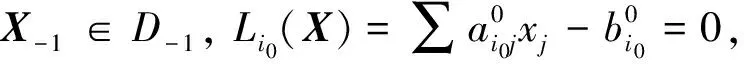
定义2 对LP做等价变换, 不失一般性, 式(1) 变为
s.t.
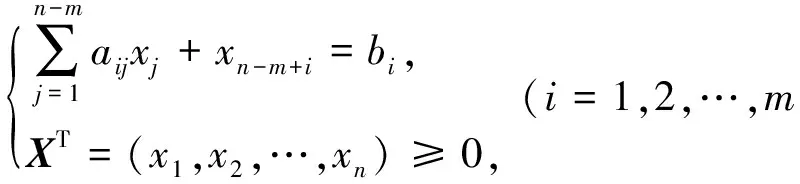

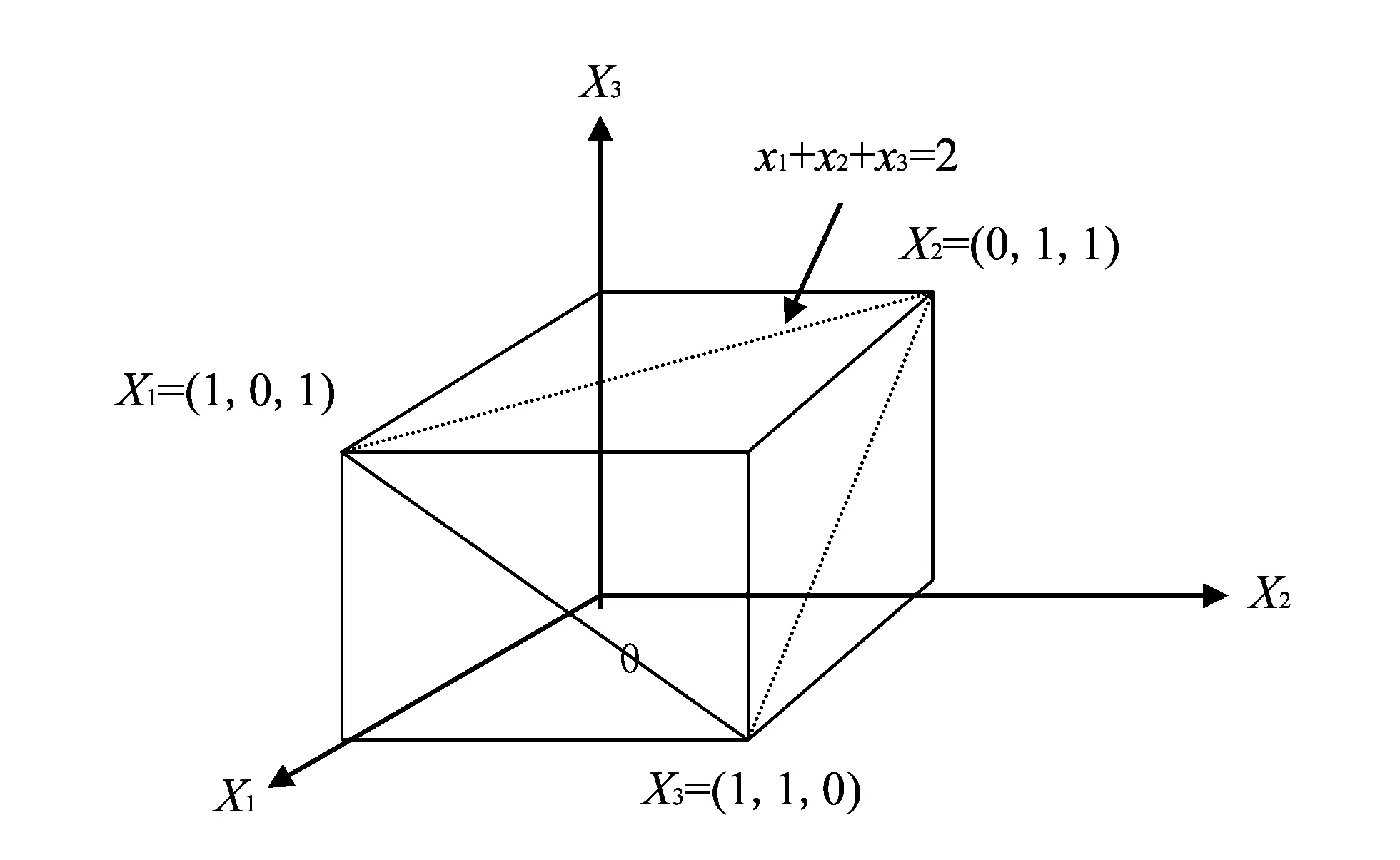
定义3 在定义2中, 若去掉xj0≥0条件, 而不影响D, 则称xj0为D的准自由变量.
定义4 若0 定义5 若0 根据仿射集合的有关理论可得出以下引理. 引理1 对于线性方程aTX=f,a=(a1,a2,…,an-m)T,X=(x1,x2,…,xn-m)T, 由Xj∈Rn-m,j=(1,2,…,n-m) 唯一确定的充分必要条件是aTXj=f, (j=1,2,…,n-m), 且线性无关. 引理3[9]∃Xj∈P(X0—δ)(j=1,2,…,n-m) 且X1,X2,…,Xn-m线性无关. 引理4[9]如下线性规划问题 s.t. 的最优值W*满足 引理5 可行解域D的维数dim(D)=n-m的充分必要条件为LP可行域D存在内点. 证明由定义1可知显然成立. 证毕. 定理2 若X0仅受限于约束条件li0=∑ai0jxj-bi0的可行解, 则 1)X0不是LP的基本可行解; 2)X0为D-1的内点. 证明1) 可直接由基本可行解的定义及定义4得出. 2) 可由可行解域的内点定义及定义4得出. 证毕. 由定义1可知: 定理3xj0为LP的非有效变量的充要条件是xj0为LP的准自由变量. 定理4 若xj0为LP的非有效变量,Li0为LP的非有效约束方程的必要条件是ai0j0≠0. 定理5 若在li0=∑ai0jxj-bi0上存在非退化的基本可行解, 则li0=∑ai0jxj-bi0一定为有效约束条件,xn-m+i0为LP的有效变量. 证明假设点X0为约束条件li0=∑ai0j·xj-bi0上非退化的基本可行解, 由线性规划问题中非退化的基本可行解的定义可知, 如果在原线性规划问题中去掉确定X0的一个约束方程, 则X0就不成为原线性规划问题的基本可行解. 即有μK≠μK-1成立, 再根据定理1可得约束条件li0=∑ai0jxj-bi0为有效约束条件, 证毕. 推论1 若xn-m+i0=0,li0=∑ai0jxj-bi0上有基本可行解, 则xn-m+i0成为原线性规划问题的非有效变量的必要条件是li0=∑ai0jxj-bi0上的基本可行解都为原线性规划问题的退化可行解. 由此, 我们可得出线性规划问题存在退化解的充分条件是该线性规划问题存在非有效变量. 由于退化解的存在, 它使得求解线性规划问题的方法复杂化. 因此, 在线性规划问题中能识别并删掉非有效变量, 不仅减少了求解线性规划问题的计算量, 而且能使解线性规划问题的复杂性简化. 推论1的逆命题不成立. 如考虑如下线性规划问题 maxZ=x1+2x2+4x3 不难分析验证:X1=(0,1,1),X2= (1,0,1),X3=(1,1,0)为线性规划问题3个退化基本可行解, 都满足约束条件x1+x2+x3=2, 而且满足约束条件x1+x2+x3=2的基本可行解仅有3个, 但对应该约束条件的松弛变量为该线性规划问题的有效变量, 如图 1 所示. 图 1 可行域的图解示意图Fig.1 The graphical diagram of the feasible region 定理6xn-m+i0为LP非有效变量,li0=∑ai0jxj-bi0为LP的非有效约束条件的充分必要条件是如下线性规划 s.t. 有最优值w*, 且有w*≤bi0成立. 证明1) 必要性. 依据定义1可得D1≌D, 再根据引理4可证. 2) 充分性. 由于w* 若w*=bi0, 则必有li0=∑ai0jxj-bi0=0和D相交, 也有线性规划 s.t. 的最优值w*=bi0, 所以D1≌D, 证毕. 定理7li0=∑ai0jxj-bi0成为原线性规划的非有效约束条件的充分必要条件是不存在仅受限于li0=∑ai0jxj-bi0约束条件的可行解. 证明1) 必要性. 设点X0为仅受限于约束条件li0=∑ai0jxj-bi0的可行解, 依据定理3可得出X0为线性规划模型 s.t. (i=1,2,…,m,i≠i0) 的一个内点. 又因为w(X0)=bi0, 则有w*>bi0成立, 依据定理2可得出li0=∑ai0jxj-bi0不能成为原线性规划的非有效约束条件, 与定理假设矛盾. 2)充分性. 由条件可知, 在li0上的任一可行解都可由其余的某些约束方程加以限制, 故约束方程li0失去了真正约束的作用, 由定义1可知li0=∑ai0jxj-bi0为LP的非有效约束条件. 证毕. 推论2 效约束条件li0=∑ai0jxj-bi0为LP的有效约束的充分必要条件是有仅受限于li0=∑ai0jxj-bi0约束条件的可行解存在. 定理8[9]若li=∑aijxj-bi为LP的有效约束条件, 则li=∑aijxj-bi上至少有n-m个基本可行解. 推论3 若原线性规划可行域D的维数dim(D)=n-m,li0=∑ai0jxj-bi0约束条件上的基本可行解的个数满足μKn-m+i0≤n-m-1, 则变量xn-m+i0为原线性规划的非有效变量,li0=∑ai0jxj-bi0为原线性规划的非有效约束. 推论4 令Li={X|li(X)=0,X∈D},xn-m+i为LP的有效变量及li=∑aijxj-bi为LP的有效约束条件的充要条件是dim(Li)=n-m-1. 推论5Kj0={Xk∶Xk∈K,xj0=0}, 若μKj0≤n-m-1, 则xj0为LP的非有效变量. 本文得出线性规划问题存在退化解的充分条件是该线性规划问题存在非有效变量, 线性规划问题非有效变量和非有效约束条件同时存在. 由于退化解的存在使得求解线性规划问题的方法复杂化, 因此, 在线性规划问题中能识别并删掉非有效变量非有效约束条件使得原模型降维数, 不仅减少了求解线性规划问题的计算量, 而且能使解线性规划问题的复杂性简化. 对线性规划问题中非有效变量的研究可为寻找和构造新的求解线性规划问题的算法提供一定的理论基础和思路. 另外, 可结合线性规划偶理论对非最优变量的识别做进一步研究. [1] 胡艳杰, 黄思明, Adren N, 等. 对偶性在线性规划预处理中的应用分析[J]. 中国管理科学, 2016, 24(12): 117-126. Hu Yanjie, Huang Siming, Adren N, et al. Analysis of using duality for presolving in linear programming[J]. Chinese Journal of Management Science, 2016, 24(12): 117-126. (in Chinese) [2] 戴彧虹, 刘新为. 线性与非线性规划算法与理论[J]. 运筹学学报, 2014, 18(1): 69-92. Dai Yuhong, Liu Xinwei. Advances in iinear and nonlinear programming[J]. Operations Research Tansactions, 2014, 18(1): 69-92. (in Chinese) [3] 敖特根. 单纯形法的产生与发展探析[J]. 西北大学学报(自然科学版), 2012, 42(5): 861-864. Ao Tegen. Analysis of the formation and development of the simplex method[J]. Journal of Northwest University (Natural Science Edition), 2012, 42(5): 861-864. (in Chinese) [4] Pan P Q. A dual projective pivot algorithm for linear programming[J]. Computational Optimization and Applications, 2004, 29(3): 333-344. [5] 杨欢, 陶凤玲, 李若东, 等. “准最优基”程序实现与应用探讨[J]. 数学实践与认识, 2014, 44(10): 219-227. Yang Huan, Tao Fengling, Li Ruodong, et al. Program realization of (quasi-optimal basis) and its application discussion[J]. Mathematics in Practice and Theory, 2014, 44(10): 219-227. (in Chinese) [6] 孙黎明. 一种求解线性规划的投影动态方法[J]. 南京师大学报(自然科学版), 2015, 38(4): 8-13. Sun Liming. A projective dynamic method for solving linear programming[J]. Journal of Nanjing Normal University (Natural Science Edition), 2015, 38(4): 8-13. (in Chinese) [7] 孟香惠, 施保昌. 线性规划单纯形法主元规则的几何分析[J]. 数学杂志, 2013, 33(2): 373-380. Meng Xianghui, Shi Baochang. Geometry analysis of pivot rules in simplex method for linear programming[J]. Journal of Mathematics, 2013, 33(2): 373-380. (in Chinese) [8] 潘平奇. 关于“线性规划界面算法的高效实现” [J]. 运筹学学报, 2015, 19(3): 78-84. Pan Pingqi. On “an efficient implementation of the face algorithm for linear programming”[J]. Operations Research Tansactions, 2015, 19(3): 78-84. (in Chinese) [9] 高引民, 甘仞初. 线性规划问题非有效约束条件性质研究[J]. 系统工程与电子技术, 2005, 27(6): 1041-1043. Gao Yinmin, Gan Renchu. Characteristics of ineffective constraints in linear programming[J]. Systems Engineering and Electronics, 2005, 27(6): 1041-1043. (in Chinese) [10] 高引民, 甘仞初, 吴立志. 线性规划非最优有效约束方程判别定理研究[J]. 太原理工大学学报, 2004, 35(3): 371-373. Gao Yinmin, Gan Renchu, Wu Lizhi. The study of characteristics of ineffective constraints in linear programming[J]. Journal of Taiyuan University of Technology, 2004, 35(3): 371-373. (in Chinese) StudyofCriteriaofLinearProgrammingwithIneffectiveVariables GAO Yin-min, CHEN Jian-bin (College of Business, Beijing Union University, Beijing 100025, China) In order to improve the characteristics of the ineffective variables and ineffective constraints, the relations between the ineffective variables and ineffective constraints were discussed. It was proved that the theorems of identifying ineffective variables and ineffective constraints which are the theoretical base of the method of identifying and eliminating further ineffective variables and ineffective constraints in solving linear programming. linear programming; feasible region; ineffective variables; ineffective constraint conditions 1673-3193(2017)03-0291-04 2016-08-22 国家自然科学基金资助项目(71572015) 高引民(1960-), 男, 教授, 博士, 主要从事运筹学、 信息系统与企业信息化的研究. O222 A 10.3969/j.issn.1673-3193.2017.03.008
2 基本定理
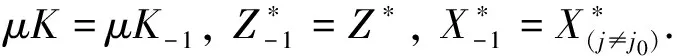
3 判别定理
4 结 语

