一类非线性Volterra-Fredholm型四重变下限无穷积分不等式*
侯宗毅
(河池学院 数学与统计学院, 广西 宜州 546300)
一类非线性Volterra-Fredholm型四重变下限无穷积分不等式*
侯宗毅
(河池学院 数学与统计学院, 广西 宜州 546300)
研究了一类积分上限为无穷大, 下限变化的非线性 Volterra-Fredholm 型四重积分不等式, 而且不等式中还有一个一重积分项. 首先利用不等式中的已知函数定义了两个新函数, 然后假定不等式中的已知函数和新函数应该满足的条件, 最后利用分析技巧, 如变量替换, 函数放大, 反函数等, 给出Volterra-Fredholm不等式中未知函数的估计.
Volterra-Fredholm型积分不等式; 无穷积分; 变下限积分; 未知函数的估计
因为Gronwall型积分不等式是研究微分方程和积分方程解的定性性质的重要工具[1], 许多学者致力于Gronwall型积分不等式的各种推广形式的研究[2-16]. 2008年, Ma等[6]研究了Volterra-Fredholm型非线性时滞积分不等式
2012年, 郑斌等[8]研究了Volterra-Fredholm型离散不等式



本文研究了Volterra-Fredholm 型变下限四重积分不等式



1 主要结论
在本文中,R表示全体实数的集合,R+∶=[0,∞),X,Y∈R+,Ω=[X,∞)×[Y,∞). 假设不等式(3)中的函数L1,L2∈C(Ω×R+,R+)满足L1(x,y,u)≤g1(x,y)u,L2(x,y,u)≤g2(x,y)u,g1,g2∈C(Ω,R+). 为了叙述定理方便, 我们利用不等式(3)中的已知函数定义两个函数
其中:

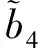
定理假设φ∈C(R+,R+)是严格增函数, 具有次可乘性, 即φ(uv)≤φ(u)φ(v), ∀u,v∈R+, 且满足φ(r)>0, ∀r>0, 由φ定义的Φ满足Φ(∞)=∞; 函数a∈C(Ω,R+)关于每个变量都是不增的, 且满足a(x,y)>0. 假设bi∈C(Ω2,R+)(i=1,2,3,4)是关于第三、 第四个变量都不增的函数, 且b1,b2至少有一个函数不恒等于零. 假设α∈C1([X,∞),[X,∞)) (β∈C1([Y,∞),[Y,∞))) 是不减函数, 且满足α(x)≥x,α(X)=X,α(∞)=∞ (β(y)≥y,β(Y)=Y,β(∞)=∞). 如果Ψ是严格增函数, 函数u∈C(Ω,R+)满足不等式(3). 则对任意(x,y)∈Ω, 有估计式
其中
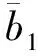

证明根据不等式(3)和L1,L2满足的条件, 我们推出




定义函数v1(x,y)为
显然,v1(x,y)关于每个变量都是不增的. 任意选取X1∈[X,∞), 暂时固定X1, 由式(15)和式(16), 得到

令函数v2(x,y)表示不等式(17)的右端, 即

求v2(x,y)关于x的导数, 得到
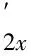

由上式可得
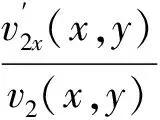
由不等式(20)可以推出

即

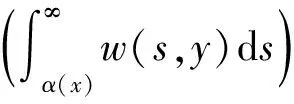
综合式(17), 式(18)和式(22), 推出

因X1的任意性, 由式(23)得到

将式(24)代入式(16)得到, 对任意(x,y)∈Ω,
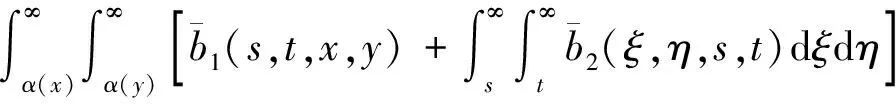
其中:

对不等式(25)进行类似于式(17)到式(24)的运算, 推出

将式(27)代入式(26), 得到
上式整理得
即
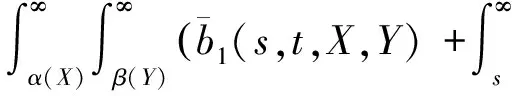
因为Ψ是严格增函数, 由上式得
将式(31)代入式(27), 利用关系式(24)得到所要的估计式(12).
[1] Gronwall T H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations[J]. Annals of Mathematics, 1919, 20(4): 292-296.
[2] Bainov D, Simeonov P. Integral inequalities and applications[M]. London: Kluwer Academic Publishers, 1992.
[3] Pachpatte B G. A note on certain integral inequality[J]. Tamkang Journal of Mathematics, 2002, 33(4): 319-325.
[4] Pachpatte B G. Explicit bound on a retarded integral inequality[J]. Mathematical Inequalities & Applications, 2004, 7(1): 7-11.
[5] Agarwal R, Deng S, Zhang W. Generalization of a retarded Gronwall-like inequality and its applications[J]. Applied Mathematics & Computation, 2005, 165(3): 599-612.
[7] Zheng B. Qualitative and quantitative analysis for solutions to a class of Volterra-Fredholm type difference equation[J]. Advances in Difference Equations, 2011(1): 1-16.
[8] Zheng B, Fu B. Some Volterra-Fredholm type nonlinear discrete inequalities involving four iterated infinite sums[J]. Advances in Difference Equations, 2012(1): 228.
[9] 王五生. 一个推广的二变量时滞积分不等式及其应用[J]. 系统科学与数学, 2010, 30(3): 425-432.
Wang Wusheng. A general form of retarded integral inequality with two variables and its application [J]. Journal of Systems Science and Mathematical Sciences, 2010, 30(3): 425-432. (in Chinese)
[10] 王五生, 李自尊. 含多个非线性项的时滞积分不等式及其应用[J]. 数学进展, 2012, 41(5): 597-604.
Wang Wusheng, Li Zizun. Retarded integral inequality with multiple nonlinear terms and its application[J]. Journal of Advances in Mathematics, 2012, 41(5): 597-604. (in Chinese)
[11] 魏巍, 乔建斌. Minkowski 不等式两种形式的推广[J]. 中北大学学报(自然科学版), 2013, 34(2): 109-111.
Wei Wei, Qiao Jianbin. The generalization of Minkowski inequality in two form [J]. Journal of North University of China (Natural Science Edition), 2013, 34(2): 109-111. (in Chinese)[12] Yan Y. Nonlinear Gronwall-Bellman type integral inequalities with maxima[J]. Mathematical Inequalities & Applications, 2013, 16(3): 911-928.
[13] 侯宗毅, 王五生. 一类非线性时滞型积分不等式及其应用[J]. 数学的实践与认识, 2014, 44(21): 316-320.
Hou Zongyi, Wang Wusheng. A class of nonlinear retarded Volterra-Fredholm type integral inequality and its application[J]. Journal of Mathematics in Practice and Theory, 2014, 44(21): 316-320. (in Chinese)
[14] Chang J, Luo D. On some generalized retarded integral inequalities and the qualitative analysis of integral equations[J]. Applied Mathematics & Computation, 2014, 244(2): 324-334.
[15] Zeng H, He Y, Wu M, et al. Stability analysis of generalized neural networks with time-varying delays via a new integral inequality[J]. Neurocomputing, 2015, 161: 148-154.
[16] 钟华, 王五生. 一类弱奇异积分不等式及其应用[J]. 中北大学学报(自然科学版), 2016, 37(5): 446-450.
Zhong Hua , Wang Wusheng. A class of weakly singular nonlinear Volterra-Fredholm type iterated integral inequality and its application to fractional integral equations[J]. Journal of North University of China (Natural Science Edition), 2016, 37(5): 446-450. (in Chinese)
AClassofNonlinearVolterra-FredholmTypeFourIteratedInfiniteIntegralInequalitywithVariableLowerLimit
HOU Zong-yi
(School of Mathematics and Statistics, Hechi University, Yizhou 546300, China)
A class of nonlinear Volterra-Fredholm type four iterated integral inequality with variable lower limit and infinite upper limit is studied, in which there is also a term of one variable integral. Firstly, two new functions are defined by known functions in the inequality, and then some conditions are assumed which should be satisfied by the two new functions and known functions in the inequality. Finally, the estimation for the unknown function in Volterra-Fredholm type integral inequality is given by analysis techniques, such as change of variable, amplification of functions, inverse function.
Volterra-Fredholm type integral inequalities; infinity integral; integral with variable lower limit; estimation of unknown function
1673-3193(2017)03-0269-04
2016-08-21
国家自然科学基金资助项目(11161018); 广西自然科学基金资助项目(2012GXNSFAA053009); 广西高等学校科研资助项目(KY2015ZD103,KY2015YB257)
侯宗毅(1971-), 男, 副教授, 主要从事微分方程及积分不等式的研究.
O175.5
A
10.3969/j.issn.1673-3193.2017.03.004

