函数列一致收敛的奥斯古德定理

邢家省， 杨义川

(1.北京航空航天大学数学与系统科学学院， 北京100191；2.数学、信息与行为教育部重点实验室， 北京100191)

函数列一致收敛的奥斯古德定理

邢家省1,2， 杨义川1,2

(1.北京航空航天大学数学与系统科学学院， 北京100191；2.数学、信息与行为教育部重点实验室， 北京100191)

研究函数列的一致收敛性的理论方法问题，在有限闭区间上，给出了判断函数列一致收敛的奥斯古德定理和狄尼定理的两种形式，对奥斯古德定理给出了两种证明方法，给出了奥斯古德定理的几个推论，沟通了相关知识的联系，并通过实例说明奥斯古德定理的应用及其理论价值。在开区间或无限区间上，给出了函数列一致收敛的判别定理，并应用于研究含参变量广义积分的一致收敛性，从理论上沟通了函数列一致收敛与参变量广义积分的一致收敛的内在联系，构成一套理论方法体系。

函数列的一致收敛性；等度一致连续；奥斯古德定理；狄尼定理

函数列的一致收敛性是经典数学分析中的重要理论课题[1-8]，具有深刻的学术发现意义，为后继理论发展提供基础，为此，人们进行了持续不断的研究。著名的狄尼定理是判断函数列一致收敛的一个充分条件[1-7]，是数学分析中的常用定理。然而判断函数列一致收敛的奥斯古德定理[1,8]在数学分析中一般不作为定理给予列出，没有得到足够的重视，导致人们在出现需要使用的场合，难于找到具体的出处[1,8-10]。其实奥斯古德定理具有重要的理论发展意义，为Arzela-Ascoli定理的发现做了准备，Arzela-Ascoli定理为连续函数空间中的列紧性理论提供了知识基础，是现代数学的一个基本理论结果，具有重要的应用价值[11-13]。

1 函数列一致收敛的奥斯古德定理

设I是一个区间，将I上的连续函数全体构成的集合记为C(I)。

设F⊂C(I)，如果存在常数M>0，对任何f∈F，任意x∈I，都有f(x)≤M，则称函数族F在I上是一致有界的[1,2,11]。

设F⊂C(I)，如果对∀ε>0,∃δ>0，当x1-x2<δ，x1,x2∈I时，便有f(x1)-f(x2)<ε，对所有f∈F成立，则称函数族F在I上是等度一致连续的[1,11]。

定理1[1,8,14]设函数列{fn}在有限闭区间[a,b]上连续，且{fn(x)}在[a,b]上一致收敛于f(x)，则有f(x)在[a,b]上的连续，且{fn}在[a,b]上等度一致连续。

定理1的证明见文献[1,8,14]。

fn(x)-f(x)≤fn(x)-fn(xk)+

fn(xk)-f(xk)+f(xk)-f(x)<3ε

这就证明{fn(x)}在[a,b]上一致收敛于f(x)。

定理3就是著名的Osgood定理，在文献[9-10]中得到应用。

定理4中的条件，来源于Osgood条件[18-19]。

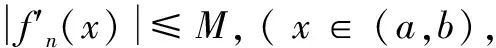
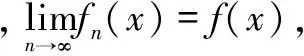
定理7的证明见文献[14]，也可以参考定理3中证法2给出相应的证明过程。

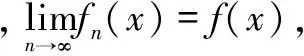
例1可以说明文献[14]中的定理5，推论2，定理6，推论3，定理7(1)都是错误的，文献[14]中所给条件不够。文献[14]中本身的例子也可以用来说明这几个结论均是不成立的。

利用文献[1,11,16-17]中方法可以给出定理8的证明。

在无限区间上，奥斯古德定理不再成立。

例2设Ω=[0,+∞)，

n=1,2,…

定理6中的极限函数f(x)未必在[a,b]上可导。

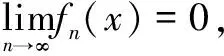
例4出现于文献[1-2]中，用的是原始证法，证明过程相当繁琐。可以利用Osgood定理给出直接的证明，从具体问题中发现一般性的规律。

例5的思想来源于文献[1-2]，例5中的函数是对文献[1-2]中给出的函数的改正。

2 狄尼定理的两种形式

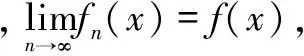
定理9就是常用的狄尼定理，在文献[1-7,15-17]中给出了另外两种证明方法。

由定理9的条件和结果，利用定理1可知{fn(x)}在[a,b]上等度一致连续，所以由定理9中的条件可推出满足定理3的条件，就是奥斯古德定理比狄尼定理广泛。

关于函数项级数和含参变量积分的狄尼定理，在文献[1-7,16-17]中已有陈述，并给出了应用。定理9的结果对开区间或无限区间的情形不再成立[1-7,15-17]。

定理10[16-17]设函数序列{fn(x)}在[a,b]上逐点收敛于函数f(x)，如果f(x)在[a,b]上连续，且对每个n，fn(x)都是[a,b]上的单调函数，则{fn(x)}在[a,b]上一致收敛于f(x)。

fn(x)-f(x)≤

fn(x)-fn(xi)+fn(xi)-f(xi)+f(xi)-f(x)≤

fn(xi+1)-fn(xi)+2ε≤

fn(xi+1)-f(xi+1)+f(xi+1)-f(xi)+

f(xi)-fn(xi)+2ε<5ε

即得{fn(x)}在[a,b]上一致收敛于f(x)。

定理10的结果，可以研究分布函数列的一致收敛性。

奥斯古德定理[1,8,14]和狄尼定理[1-7,14,16-17]的两种形式，构成判断函数列一致收敛的一套完整的理论体系。

3 开区间或无限区间上一些函数列一致收敛的判别定理及应用

利用定理11的证明方法，可以得到如下两个结果。

证明设

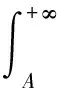
在[u0,U]上是一致的。

例6在文献[1,2,17]中，用的是原始证法，没有上升为一般性的理论方法。本文发现可以利用一般性的理论结果给出简单的证明，从具体问题中发现一般性的理论。

[1] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002.

[2] 常庚哲,史济怀.数学分析教程(下册)[M].北京:高等教育出版社,2003.

[3] 黄玉民,李成章.数学分析(下册)[M].2版.北京:科学出版社,2007.

[4] 华罗庚,著.王元,校.高等数学引论(第二册)[M].北京:高等教育出版社,2009.

[5] 陈纪修,於崇华,金路.数学分析(下册)[M].2版.北京:高等教育出版社,2003.

[6] 菲赫金哥尔茨.微积分学教程(第二卷)[M].8版.北京:高等教育出版社,2006.

[7] 卓里奇.数学分析(第二卷)[M].4版.北京:高等教育出版社,2006.

[8] 杨小远,邢家省.工科数学分析习题及题解集[M].北京:机械工业出版社,2010.

[9] 邢家省,朱建设.非齐次弦振动方程的形式级数解的收敛性[J].吉首大学学报,2009,30(5):13-17.

[10] 邢家省,张愿章,郭秀兰.非齐次热传导方程初边值问题的形式级数解的收敛性[J].河南科学,2010,28(1):1-5.

[11] 陈国旺.索伯列夫空间导论[M].北京:科学出版社,2013.

[12] 郭金海.奥斯古德与函数论在中国的传播[J].中国科技史杂志,2014,35(1):1-15.

[13] 邢家省,杨小远,白 璐.两无穷区间上积分交换次序充分条件的改进及其应用[J].四川理工学院学报:自然科学版,2016,29(1):87-92.

[14] 徐丽.函数列一致连续和一致收敛及等度连续的关系[J].上海电力学院学报,2007,23(3):284-286.

[15] 叶艺林.狄尼定理的多种证明[J].景德镇高专学报,1998,13(4):30-32.

[16] 匡继昌.实分析与泛函分析(续论)(下册)[M].北京:高等教育出版社,2015.

[17] 汪林.数学分析中的问题研究和反例[M].北京:高等教育出版社,2015.

[18] 徐润,吕玉华.关于Osgood 条件的进一步讨论[J].沈阳师范大学学报:自然科学版,2005,23(4):347-348.

[19] 孔志宏.一阶微分方程存在唯一性定理的几个注记[J].高等数学研究,2016,19(3):3-6.

[20] 邢家省,杨义川,王拥军.函数列的广义积分的极限定理及其应用[J].吉首大学学报:自然科学版,2016,37(6):1-9.

[21] 邢家省,杨义川,王拥军.函数列的黎曼积分的极限定理及其应用[J].四川理工学院学报:自然科学版,2017,30(3):73-78.

[22] 高建全,邢家省,杨义川.两无穷区间上广义积分交换次序定理[J].河南科学,2017,35(6):845-851.

The Osgood Theorem of Uniformly Convergent Functions

XINGJiasheng1,2,YANGYichuan1,2

(1.School of Mathematics, Beihang University, Beijing 100191, China;2.LMIB of the Ministry of Education, Beijing 100191, China)

Considering the theoretical method of uniformly convergent functions, Osgood theorem and the Dini theorem on the finite interval are given to judge the uniform convergence of Function column. Then two proof methods of Osgood theorem and its inference are given. And through the examples, the theoretical value of Osgood theorem is illustrated. Discriminant theorem of uniform convergence of function in open or infinite interval have been given and applied in studying the uniform convergence of generalized integrals with parametric variables which theoretically communicating the intrinsic relations between the uniform convergence of the function and the uniform convergence of the parameter generalized integral, and forming a set of theoretical method system.

uniform convergence of function; uniform equicontinuous; Osgood theorem; Dini theorem

1673-1549(2017)06-0083-06

10.11863/j.suse.2017.06.15

2017-08-06

国家自然科学基金资助项目(11271040)；北京航空航天大学校级重大教改项目(201403)

邢家省(1964-)，男，河南泌阳人，副教授，博士，主要从事偏微分方程、微分几何泛函分析方面的研究，(E-mail)xjsh@buaa.edu.cn

杨义川(1970-)，男，甘肃天水人，教授，博士，主要从事逻辑代数、序代数、软计算及其应用方面的研究，(E-mail)ycyang@buaa.edu.cn

O177.2

A