基于霍夫变换的QPSK信号盲处理结果可信性评估*

鲍安平,胡国兵,金 明

(1.东南大学自动化学院,南京 210096;2.南京信息职业技术学院电子信息工程学院,南京 210023;3.金陵科技学院电子信息工程学院,南京 211169)

基于霍夫变换的QPSK信号盲处理结果可信性评估*

鲍安平1,2*,胡国兵3,金 明2

(1.东南大学自动化学院,南京 210096;2.南京信息职业技术学院电子信息工程学院,南京 210023;3.金陵科技学院电子信息工程学院,南京 211169)

为了有效评估QPSK信号盲处理结果可信与否,提出了一种基于霍夫(Hough)变换的评估算法。该方法在缺乏信号先验知识的条件下,根据调制识别结果及相应参数估计结果构造辅助信号,将辅助信号与观测信号作相关累加。以相关累加模值曲线特征为依据,将QPSK信号处理结果的可信性评估问题转化为对Hough变换极值点聚类数是否为1的检验。计算机仿真结果表明,当信噪比大于等于-2 dB时,算法的平均校验正确率大于93%。

盲信号处理;可信性检验;Hough变换;QPSK信号

在非协作信号处理中,如电子侦察,通信对抗等领域,信号处理分前端与后端两个环节。前端处理的主要包括信号的检测、调制方式的识别及主要参数的估计,后端的处理则根据应用要求的不同进行定义,如对敌方信号的干扰、跟踪,或对个体辐射源的指纹识别等。显然,前后两个环节处理的性能是存在一定关联的,前端处理的结果作性能直接影响导致后端处理的效果。若能针对前端每一次处理结果的可信性评估,即给出处理结果可信性与否的统计判决信息,这样传递到后端,后端就可以根据这一信息决定是否执行进一步的处理环节。如果前端处理的不可信,则可以将此结果抛弃,或重新处理,这样一方面可提高整个处理环节的有效性与可靠性,另一方面对处理资源也是一种节约。近年来,在电子侦察领域,对接收机前端信号处理结果的可信性评估已成为相关领域的热点课题,但在非协作条件下,由于缺乏信号的先验信息,可供处理的样本本身也较少,使得这一问题具有很大的挑战性[1]。

目前,关于信号盲处理结果可信性评估的方法主要有两类,一类是基于似然比方法,另一类是基于统计特征方法。文献[2]提出一种基于似然函数特征分析的调制方式识别可信度评估算法。以不同调制情形下似然函数为基础构造特征向量,并以向量的信息熵作为可信度评估的依据。但该方法需要信号的先验信息,计算复杂度较高,且若待识别信号库容量较小时,信息熵的评估精度难以保证,在非协作条件下也较难应用。文献[3]在用神经网络分类器对认知无线电信号进行调制识别时,以分类器的最大与次大输出值之间差值的作为分类器的可信度度量。但由于神经网络分类器本身在进行识别时,需要要依赖大量的训练样本,导致此法在非协作信号处理中难以实用。针对非协作条件下信号调制方式识别及参数估计结果的可信性评估,显得更有实用价值。此类研究将调制方式识别与参数估计视为一个整体,称之为信号盲处理。相关文献针对雷达脉内分析中常用调制信号,利用幅度、相位等特征,对其盲处理结果的可信性进行了统计分析。文献[4]提出一种基于相关累加模值线性回归失拟检验的BPSK信号盲处理结果可信性评估算法,该方法不需要信号的先验信息,但因在进行线性回归失拟检验时,需要对样本进行聚类处理,聚类数的不确定的对评估算法韧性存在一定影响。针对BPSK信号,文献[5]分析了不同可信性假设一下特定参考信号与原始观测信号相关后相位分布的差异,提出了一种基于Kolmogorov-Smirnov分布拟合检验的信号盲处理结果可信性评估算法。但该算法需对信噪比进行估计且信噪比低(小于-6 dB)时性能较差。文献[6]研究了LFM信号盲处理结果可信性评估算法。在分析特定参考信号与观测信号相关序列谱中循环频率特征差异的基础上,通过检测相关序列在零频率附近是否存在循环频率,实现对LFM信号盲处理结果的可信性检验。首先对观测信号进行调制方式识别及参数估计,建立参考信号后,将观测信号与参考信号作相关运算并作DFT,该方法利用了频域信息,其处理信噪比门限可达到-15 dB。

QPSK在雷达与通信中都是一种常用的调制信号,但现有文献仅针对BPSK信号,LFM信号盲处理结果的可信性评估问题进行了研究。针对QPSK信号盲处理结果的可信性评估的相关文献,尚未见发表。本文先根据对QPSK信号的处理结果及相应的信号参考模型,建立辅助信号,并将之与原始信号作相关累加,而后将QPSK信号的可信性评估问题建模为对相关累加曲线的Hough变换峰值点聚类是否为1的特征检验问题。仿真结果表明,当信噪比大于等于-2 dB时,算法的平均校验正确率大于93%。

1 基本模型与假设

假定QPSK信号模型为

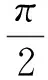
(1)

式中:A为信号幅度,f0为载频,φ是初始相位,N为样本个数,Δt为离散采样间隔,d2(n)是四元编码信号,取值为0,1,2或3,其码元持续时间为Tc。叠加了高斯白噪声的QPSK原始观测信号可表示为,

x(n)=s(n)+ω(n)=

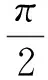
(2)

式中:ω(n)是复零均值限带高斯白噪声,其实部与虚部相互独立,方差为2σ2;信噪比为γ=A2/2σ2。

若用特定的处理算法,将观测信号识别为QPSK信号后,对QPSK信号的解调,一般采用四次方法。具体为[7]:

(1)将QPSK信号降阶为正弦波信号,通过对转换得到的正弦波信号进行载频(将正弦波信号的载波估计值除以4)得到其载频估计。

(2)利用载频估计值,经适当变换,将观测信号转换到基带;

(3)以基带信号为依据,对QPSK信号进行码元宽度、码元个数估计,并进行解码。

从上述过程可以见,QPSK信号的解码是否准确,主要取决于其前续的调制方式识别、载频估计、码元宽度等参数估计的准确与否。显然,如果这些前续环节处理的性能较好,即调制方式识别正确且各参数估计的结果误差较小,则发生解码错误的可能性也较小,此时,我们称此次处理结果的可信;反之,若调制方式识别错误,或者虽然识别结果正确,但其他参数估计偏差大,则此时解码发生错误的可能性也较大,则称此次处理结果的不可信。换言之,解码结果是否存在错误,某种意义也表征了整个处理环节的可信性。为此,我们可将QPSK信号盲处理结果的可信性检验归结为如下假设检验问题:

H0:无解码错误;H1:存在解码错误。

(3)

本文后续的分析将聚焦于如何根据信号的某一次处理结果及观测信号本身,提取用以表征处理结果可信性的统计量,对式(3)给出的模型进行假设检验。

2 Hough变换

Hough变换于1962年由Paul Hough提出,并在美国作为专利被发表。Hough变换是一种常用于图像中直线检测的特征提取技术,广泛应用于图像分析、雷达信号检测和时频参数估计等领域[8]。其实质是构造一个数据空间向参数空间的一对多的映射,在参数空间把全局检测转化为局部峰值检测。Hough变换是在二值化数字图像中进行形状检测的一种技术,可用于对直线、图及椭圆的检测,但要求这些图形能用数学表达式进行描述。此处,仅限于介绍Hough变换应用于直线检测的情形。其基本思想为:如果二进制图像中存在一个白色相素点,则肯定有很多条直线通过这个单相素点,同时这些直线与会通过其他白色相素点。在一条线上的白色相素点越多,越可以判定其可表示为一条直线。

对于一条直线,其数学表达为:

y=ax+b

(4)

式中:a为直线y的斜率,b为其在y轴上的截距。可以认为参数(a,b)张成的空间代表了一系列的直线。我们称这种直角坐标系下的空间为数据空间,它具有一个缺点,就是当直线越来越接近垂直线时,参数(a,b)均趋于无穷大。因此,可以采用另一种有边界的表达方式,即极坐标参数空间(ρ,θ)来表达直线,如图1所示,ρ表示从原点到直线的距离,θ表示其垂线与x轴之间的夹角。这样式(4)可写为:

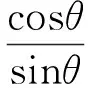
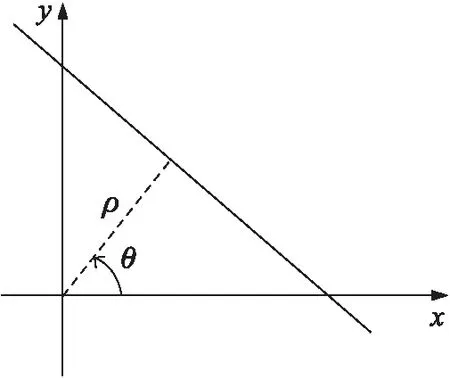
图1 直线的极坐标表示

进一步,将上式写成

ρ=xcosθ+ysinθ

(5)

式(5)表明,可将直线从直角坐标系的(a,b)空间转换到极坐标空间(ρ,θ),后者也称之为Hough空间。本文将试图将QPSK信号的可信性评估与Hough变换联系起来。

3 QPSK信号盲处理结果可信性特征分析

3.1 可信性评估特征分析

根据式(3)定义的可信性评估假设检验模型,可分为两种情形,即

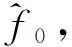
将辅助信号与原始观测信号作相关累加运算,有

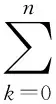
(6)

其中信号部分

(7)

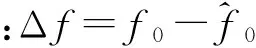
s0(n)≈A(n+1)ejφ

(8)

由式(8)可见,相关累加序列信号部分的模近似为关于变量n的线性函数,其幅角近似为常量。进一步,对相关累加序列取模得到

|z(n)|=|s0(n)+ω0(n)|

(9)

将ω0(n)写成极坐标形式为ω0(n)=Rω(n)×ejφω(n),其中Rω(n),φω(n)分别为其模值与幅度,则有

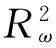
(10)

考虑到相关累加时,信噪比增益随相关累加长度n而增加,当n1时,相关累加值的信噪比一般较大,此时≼1,式(10)中的二次项≈0。于是,式(10)可继续写为

(11)

式中:等效相位函数β(n)=φ-φω(n),为[0,2π)上的随机相位序列。将式(11)开方,并进行级数展开,得到

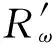
(12)

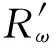
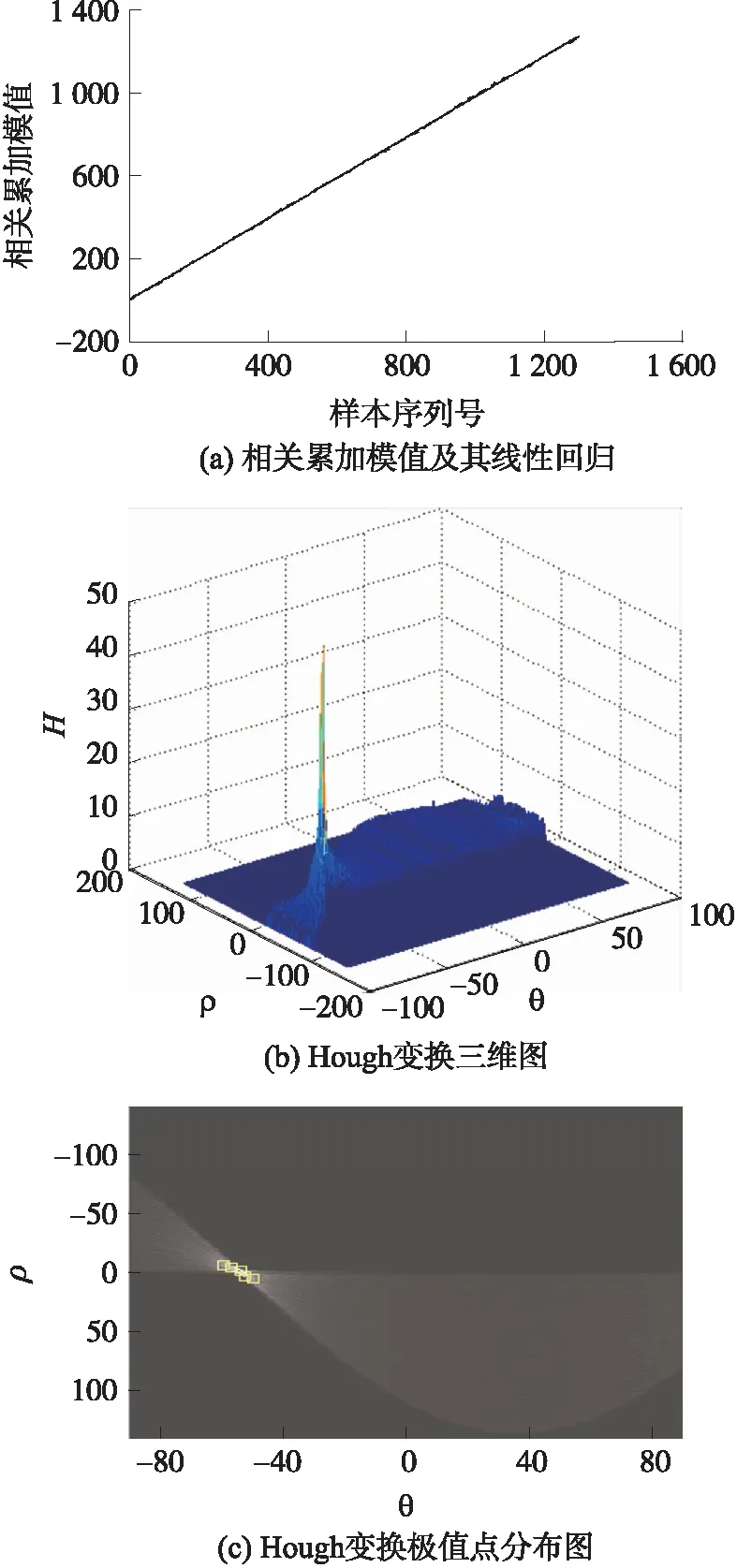
图2 在H0假设下相关累加模值及其Hough变换

令x=n,y=|z(n)|,根据Hough变换的映射公式(见式(5)),可将相关累加模值序列映射到Hough空间,得到(H,ρ,θ)=Hough(x,y),式中H为Hough变换的幅值。显然,H0假设下,对相关累加模值的Hough变换,其只出现一个峰点,而且由于是对同一条直线进行累加,峰值较大,如图2(b)及2(c)所示。

(2)在H1假设下:即QPSK信号存在错误解码,此时可能出现两种情形

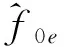
(13)

并将观测信号x(n)与之作相关累加,得到:

式中:ω1(n)为噪声项,而信号部分

(14)

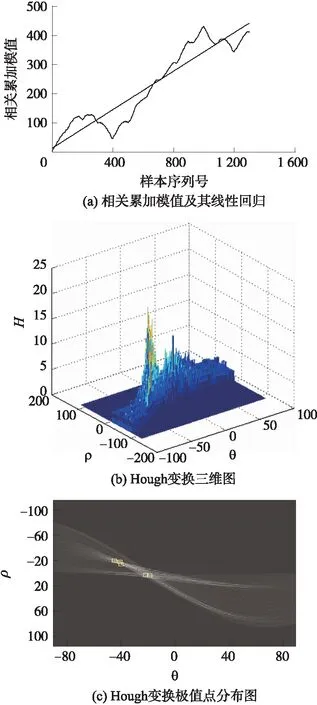
图3 QPSK信号误识为NS信号时相关累加模值及其Hough变换

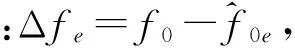
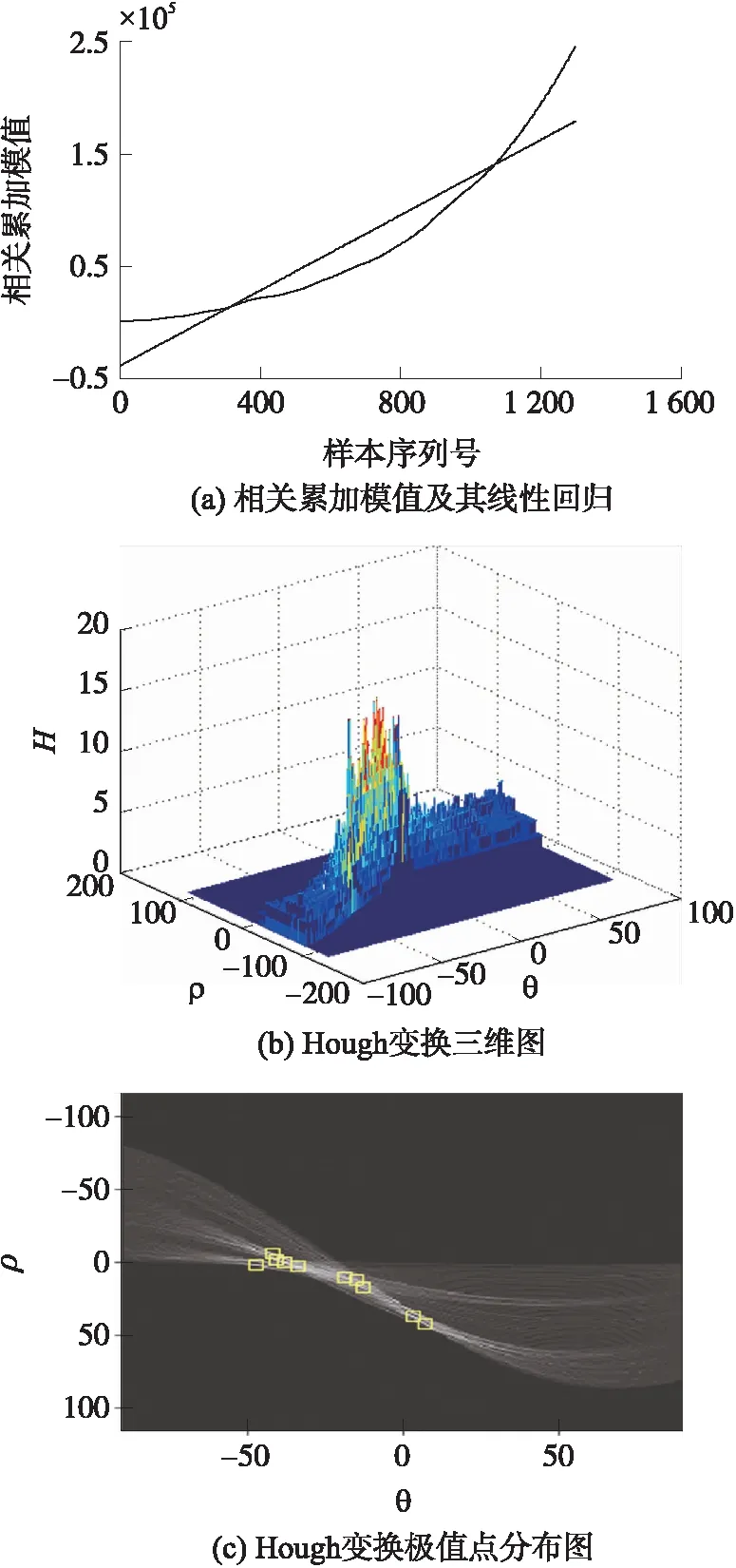
图4 QPSK信号误识为LFM信号时相关累加模值及其Hough变换

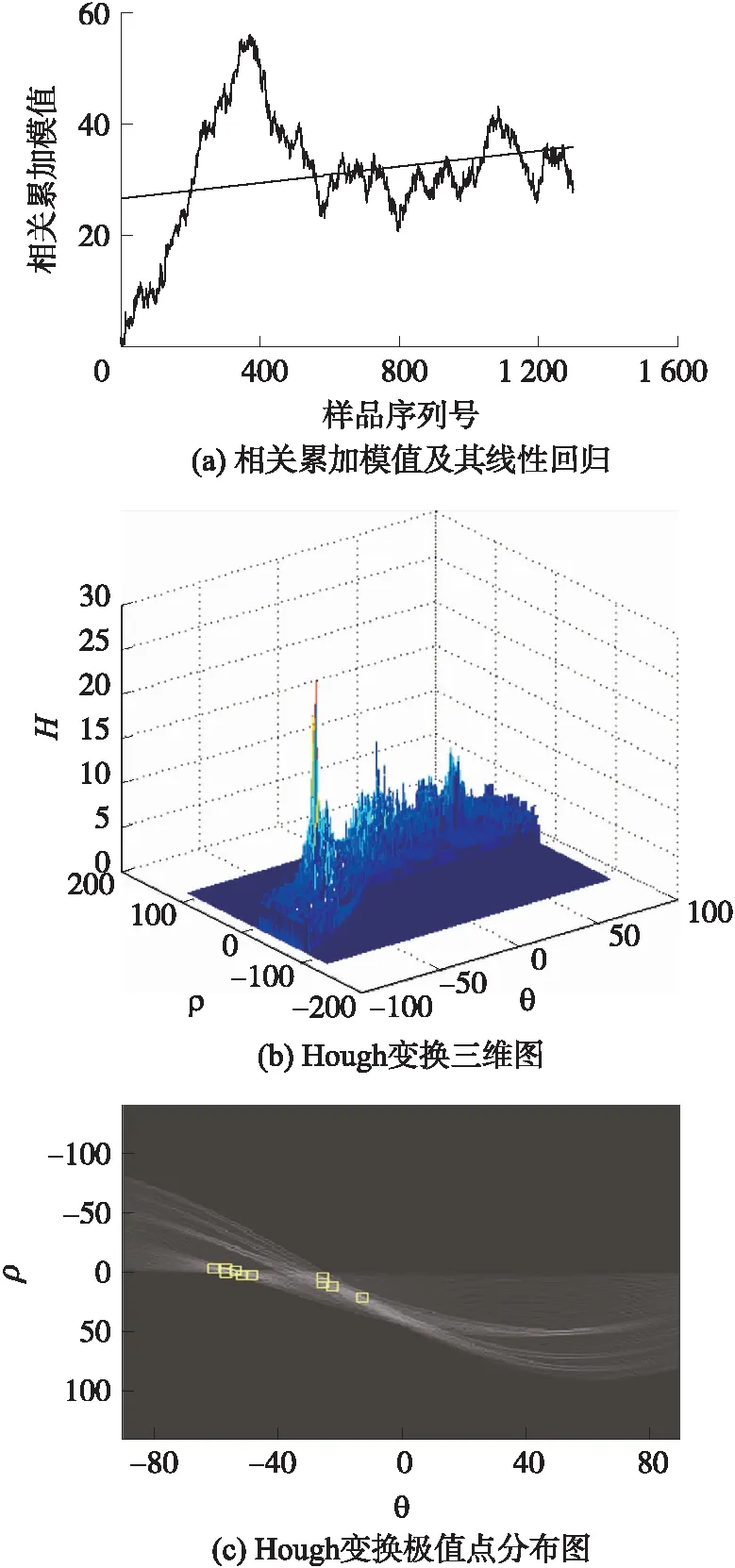
图5 QPSK信号误识为BPSK信号时相关累加曲线及其Hough变换

(b)调制方式识别正确,但存在解码错误:由于信噪比较低或其他因素,特征量虽然属于QPSK的特征空间,但处于特征空间的边缘或者由于处理信噪比接近信噪比门限,导致某次参数估计的结果误差偏大,从而产生了解码发生部分错误。图6(a)所示为QPSK虽然误别正确,但频偏为0.5倍量化频率间隔且存在1位解码错误时,相关累加模值|z(n)|及其线性回归值示意图。由图6可见,由于存在较大的频率估计误差,且存在解码错误,所以相关累加模值在发生解码错误位置前后的曲线斜率符号不同,且整个曲线的其他也呈曲线形状,不呈直线。显然,此时对相关累加模值|z(n)|作Hough变换,也会存在多个极值点,且极值点的幅度比H0假设时小,如图6(b)、图6(c)所示。

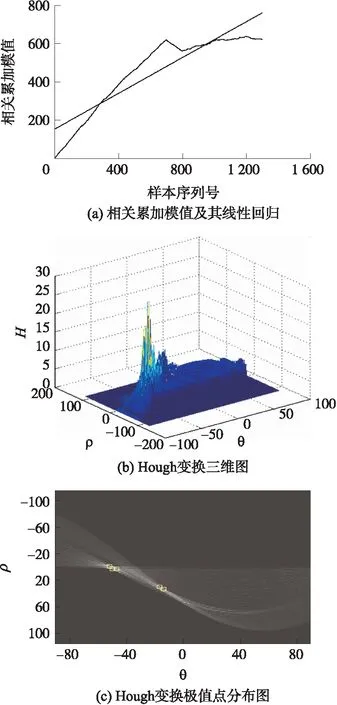
图6 QPSK信号识别正确,但存在一位解码错误时的相关累加模值及其Hough变换(频偏为0.5倍量化频率间隔)

3.2 可信性评估算法

综前所述,可知:

(1)在H1假设下,相关累加模值呈现为一条噪声背景下的直线,在Hough变换空间只有一个峰点,且峰值较大;

(2)H1假设下各种失配情形极值点分布各不同相同,分散成若干组,明显不属于同一条直线,此时极值点可能有多个,且各极值的大小比H0假设下时小。

实际中,在一个极值点附近可能会检测到若干大小相近的若干极值点,形成不同的分组。图2～图6各图中(c)子图所示为不同情形下相关累加曲线模值经Hough变换后检测到极值点分布图。由图可见:不同情形下,其极值点分布各不同相同,H0假设下,检测到的极值点基本重合,属于同一组,聚成一类,对应于一条直线,且类内的均值较大;H1假设下的各种情形,极值点分散成若干组,检测出来的不属于一条直线或者不呈直线,此时极值点聚类数将大于1,而且不同类的均值也一般较小。若定义

C1=Count[Hough(|z(n)|]

(15)

式中:Count[Hough(|z(n)|]表示统相关累加模值z(n)的Hough变换极值点聚类数的统计,则QPSK信号盲处理结果的可信性评估规则为

若C1=1,则H0假设判成立,否则H1成立。

(16)

本文所提出的基于Hough变换的信号盲处理结果可信性检验算法小结如下:

(1)辅助信号构建:利用特定处理算法得到调制识别结果及参数估计结果,基于识别结果对应的信号模型建立辅助信号;

(2)相关累加:将辅助信号与观测信号作相关累加运算,取其模值|z(n)|;

(3)Hough变换:先将相关累加曲线|z(n)|转称成一幅二值化的二维图像,经边缘检测处理后作Hough变换,并进行峰值点检测;

(4)统计判决:对检测出的峰值点进行聚类,若C1=1,则判H0成立,否则判H1成立。

4 性能仿真与分析

假设接收到的观测信号x(n)为被加性高斯白噪声污染的QPSK信号,载频10.05 MHz,码元宽度1 μs,采样频率fs=100 MHz,样本长度为1 300点,仿真次数10 000次。仿真所用调制识别算法采用文献[9-10]方法,QPSK信号的参数估计方法采用文献[7]提出的处理算法,Hough变换极值点聚类方法选择K均值法[11]。以下各表中:nij,i=0,1,j=0,1表示对于某一次具体的盲处理结果而言,实际为Hi假设,利用Hough变法检验算法判为Hj的次数。此处,定义平均校验正确率为Pc=(n11+n10)/Ns(其中Ns表示为总的仿真次数)作为评价可信性评估算法性能的指标。

实验1码序列为13位随机序列

表1所示为利用Hough变换法对13位随机序列QPSK信号盲处理结果的可信性进行处理时的统计性能。由表1可见,本算法的平均校验正确率随信噪比的增加而增加。当信噪比大于-0 dB时,利用本算法对BPSK信号处理结果进行可信性检验的平均校验正确率大于99%。信噪比变小,10 000次仿真中的不可信性处理次数相应增加。信噪比为-2 dB时,本算法可将3 948次不可信处理的情形中的3 444次检出,5 952次可信性处理中5 938次认定为可信处理,平均正确校验检错率达93%以上。信噪比小于-4 dB时,10 000次仿真中,出现不可信处理的次数增加骤增,本算法对可信性处理的校验率仍较高,可将944次可信处理认定为可信,而对不可信性处理的校验性能变差,导致平均校验正确率降到38.5%,。当信噪比进一步下降至-4 dB以下,本算法失效。

实验2码序列为31位随机序列

表2所示为利用Hough变换法对31位随机序列QPSK信号盲处理结果的可信性进行处理时的统计性能。当信噪比大于-2 dB时,利用本算法对BPSK信号处理结果进行可信性检验的平均校验正确率大于99%。信噪比-4 dB时,本算法平均校验正确率小于降到52.44%,算法失效。但相比表1而言,本算法对31位随机序列QPSK信号的可信性校验性能更佳,信噪比门限约下降2 dB,原因在于码元个数的增加,实际上就是增加了信号的样本数,而相关累加序列的信噪比增益随样本数而增加,这样Hough变换极值点的幅度也有所增加,从而有利于对QPSK信号盲处理结果的可信性校验。

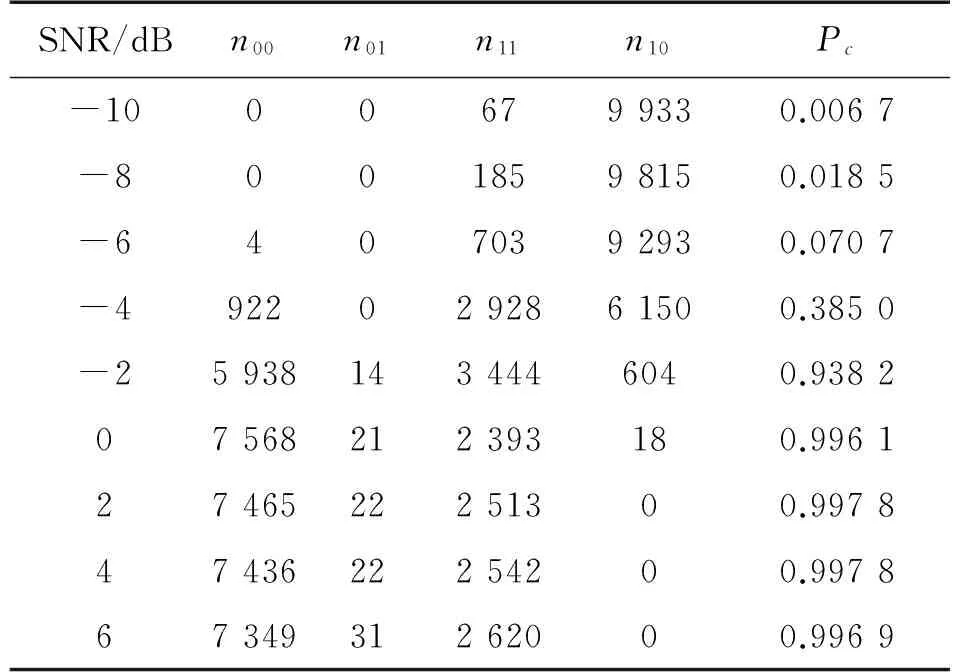
表1 不同信噪比时的检验性能(13位随机序列)

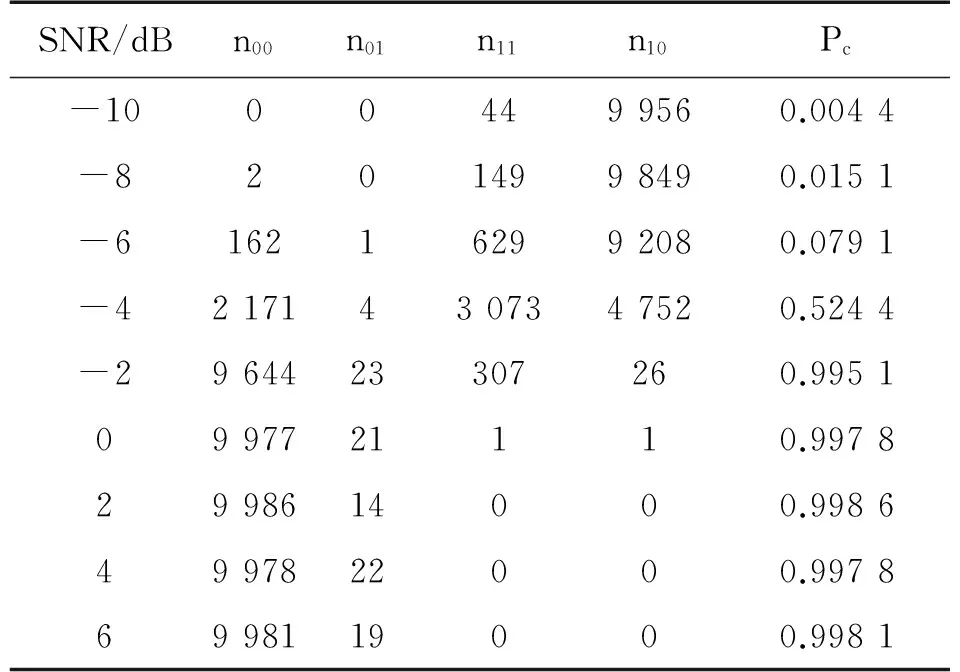
表2 不同信噪比的检验性能(31位随机序列)

5 结束语

本文将数字图象处理中常用的Hough变换引入到QPSK信号盲处理结果的可信性校验中,提出一种基于Hough变换极值点特征的处理算法。先根据盲处理结果构造辅助信号,并将辅助信号与原始观测信号作相关累加,而后对相关累加模值序列作Hough变换,提取其极值点的聚类数作为特征量,完成对QPSK信号盲处理结果可信与否的判定。文中分别以13位、31位随机序列QPSK信号为例,进行了联合仿真,结果表明,该算法在较低信噪比时仍有效,且性能随码元个数的增加而增加。本算法可在缺乏信号先验信息的条件下工作,在电子情报分析中具有一定的理论与实用价值。

[1] W Su J A K,Y Ming. Dual-Use of Modulation Recognition Techniques for Digital Communication Signals[C]//Systems,Applications and Technology Conference. 2006:1-6.

[2] Lin W S,Liu K J R. Modulation Forensics for Wireless Digital Communications[C]//IEEE International Conference on Acoustics,Speech and Signal Processing,2008. ICASSP 2008. 2008:1789-1792.

[3] Fehske A,Gaeddert J,Reed J H. A New Approach to Signal Classification using Spectral Correlation and Neural Networks[C]//2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks,2005. DySPAN 2005. 2005:144-150.

[4] 胡国兵,刘渝. BPSK 信号盲处理结果的可靠性检验算法[J]. 数据采集与处理,2012,26(6):637-642.

[5] 胡国兵,徐立中. 基于K-S检验的BPSK信号盲处理结果可信性评估[J]. 电子学报,2014,42(10):1882-1886.

[6] 胡国兵,徐立中,吴珊珊,等. 基于循环平稳分析的LFM信号盲处理结果可靠性评估[J]. 电子学报,2016,44(4):788-794.

[7] 朱霞,刘渝,狄慧. 一种低信噪比条件下QPSK信号盲处理方法[J]. 数据采集与处理,2011,26(5):553-558.

[8] Barbarossa S. Analysis of Multicomponent LFM Signals by a Combined Wigner-Hough Transform[J]. IEEE Transactions on Signal Processing,1995,43(6):1511-1515.

[9] 胡国兵,刘渝. 基于正弦波抽取的雷达脉内调制识别[J]. 计算机工程,2010,36(13):21-23.

[10] 陈役涛. 雷达信号调制方式识别可信度研究[D]. 南京:南京航空航天大学,2008.

[11] HARTIGAN J A. Clustering Algorithms[M]. New York:John Wiley,1975:38-41.

ReliabilityTestforBlindProcessingResultsofQPSKSignalsUsingHoughTransformation*

BAOAnping1,2*,HUGuobing3,JINMing2

(1.School of Automation,Southeast University,Nanjing 210096,China;2.Nanjing College of Information and Technology,Nanjing 210023,China;3.School of Electronic and Information Engineering,Jinling Institute of Technology,Nanjing 211169,China)

In order to assess the reliability of the QPSK signal processing results,an algorithm based on Hough transform is proposed. In the absence of a priori knowledge of the signal,by constructing an auxiliary signal based on the modulation and the corresponding parameter estimation results,the correlation sum between the original observed signal and the auxiliary signal is obtained. Based on the characteristics of the correlation modulus curve,the reliability test of blind signal processing is transformed to a test of whether the cluster number of the peaks of the Hough transformation is 1. The computer simulation results show that the average correct verification rate of the proposed algorithm is greater than 93% when the SNR is greater than -2 dB.

blind signal processing;reliability test;Hough transformation;QPSK signal

10.3969/j.issn.1005-9490.2017.06.030

项目来源:江苏省高校“青蓝工程”科技创新团队(2016年)项目(229150203/007);江苏省第十二批六大人才高峰项目(DX022)

2017-01-26修改日期2017-04-11

TP302

A

1005-9490(2017)06-1483-07

鲍安平(1974-),男,汉族,安徽芜湖人,南京信息职业技术学院教师,东南大学自动化学院博士在读,副教授、博士在读,主要研究方向为检测技术,baoanpingseu@163.com。